基于实测数据的西北地区风电场风场及尾流特性分析
李万润 栾雪涛 王雪平 杜永峰,3 李爱群
(1兰州理工大学防震减灾研究所,兰州 730050)(2东南大学土木工程学院,南京210096)(3兰州理工大学西部土木工程防灾减灾教育部工程研究中心,兰州 730050)
随着世界经济的快速发展,人们对于能源特别是电力的需求日益增长,而利用石油、煤炭等化石能源所带来的问题也日益严重.为解决这一矛盾,发展清洁能源例如风能、太阳能已成为当代能源事业发展的主流,其中风能作为一种清洁能源且可循环利用,被广泛应用于风帆助航、风车提水和风力发电等技术领域,特别是在风力发电技术的应用与发展方面,国内外已经发展的比较成熟.然而,提高发电效率一直都是风力发电技术所面临的一项重大挑战.在实际工程中,多风向多台风机尾流叠加的作用是最普遍的,它不仅会直接影响风机的布置及其发电效率[1],还会对风电场内的风特性造成一定影响,进而使下游风力机的疲劳荷载发生改变,严重时会引起结构破坏[2-5].
现有研究给出了一些指标来指导风电场风机布置和评判发电效率.Jensen模型[6-7]是目前很多风电场微观选址软件中使用的尾流模型之一,在实验和工程实践中,人们对Jensen模型进行了改进和修正,并提出了更加适用于远场尾流的修正模型.曾利华等[8]推导建立了更加完整合理的一维非线性扩张尾流模型及尾流叠加计算模型.杨祥生等[9]基于Park模型尾流区线性膨胀假设和径向风速呈高斯分布假设,提出一种新型工程尾流模型Park-Gauss模型.田琳琳等[10]采用修正的Jensen尾流模型模拟机组之间的尾流干扰效应,对平坦风电场机组布局进行优化.Lissaman[11]基于风力机任意阵列下的尾流计算模型研究,对不同风向下风能利用率和不同高度处的风速亏损做了相关研究.Frandsen等[12]通过研究大气湍流和尾流对风力机的疲劳荷载,提出风力机间的距离是影响疲劳荷载增加的一个重要参数.
虽然国内外对风场的尾流特性已有一些研究,但是基于实测数据的对比研究还相对较少.因此,本文基于实测资料对现有理论模型进行验证分析,并对尾流作用下的风场特性进行详细研究,为今后风电场设计提供依据.
1 工程背景
该风电场位于甘肃省武威市西北部约69 km处的荒漠戈壁,地貌单一,地形较为平坦,整体上东北高、西南低,多风沙天气.该风场设计安装150台单机容量2.0 MW的风力发电机组,正北向风机布置间距为5倍叶轮直径,轮毂高度80 m,叶轮直径105 m,切入风速3 m/s,切出风速20 m/s,额定风速11 m/s,风电场风机布置位置如图1所示.

图1 第二风场布置图
为便于掌握风机周围风场特性及对风机进行控制,在风机上安装了风机状态监测与监控系统.本系统中,风速分析采用三杯风速风向传感器进行监测,该风速仪风速测量范围为0~60 m/s,测量精度±0.3 m/s;风向测量范围为0°~360°,精度±1°.
本文利用第二风场2015-10—2016-08期间的风速仪监测数据,对该风场的风特性开展研究.鉴于当地实测主导风向为正北方向,为了尽量减少除尾流作用外其他因素的干扰,选取正北方向上风场外围74#风塔至场内64#风塔做详细研究,并假设处于边界上的风机不受其他风机尾流的影响.
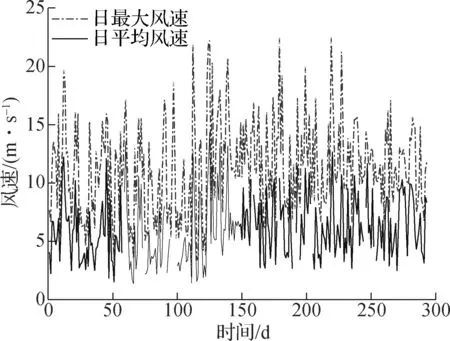
图2 观测期间日平均风速与日最大风速

图3 日最大风速统计直方图
2 风机尾流模型
2.1 模型推导
目前,在尾流区速度分布研究中常用的尾流模型有无黏近场尾流模型、简化尾流模型、Jensen尾流模型,其中Jensen模型是风电场微观选址应用最广泛的尾流模型.Jensen模型表达式为
(1)
式中,v0为来流风速;r0为风力机叶轮半径;x为风轮下游某点到风轮平面的水平距离;v为风力机下游x处尾流区的风速;α为尾流半径随x的增长率.图4给出了该模型的示意图.
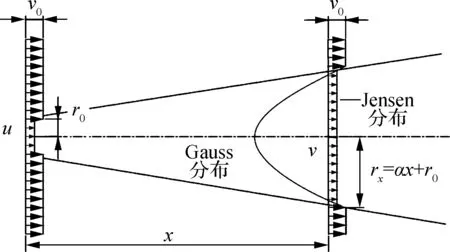
图4 尾流模型示意图
在理想风机情况下,Jensen模型一般假定u=v0/3,风能利用系数Cp=16/27.而实际运行的风力机风能利用系数Cp<16/27,于是张晓东等[6]对Jensen模型进行了改进,其表达式为
(2)
式中,k为尾流下降系数,可根据风场实测结果确定;a为轴向诱导因子.该模型在对图4所示的控制体使用质量守恒定律时,Jensen模型忽略了近场的入口流量损失和远场的流量恢复过程.假设入口截面半径为风轮半径,在远场尾流区,流管内速度回升,流管向内收缩,尾流内外的速度梯度产生压差,必然有一部分空气通过侧边界流入控制体中,控制体在近场的入口流量损失得到补充.离开风力机后越远,尾流内外的压差越小,流入控制体的气流也越少,直至无穷远处降为零,此时尾流完全恢复至与上游来流相同的参数.
由前所述,设风力机下游x处流入控制体的空气流量随x呈指数关系递减,则Jensen模型表达式修正为
(3)
式中,β为修正系数;d为风力机叶轮直径.
为了获得更加真实的尾流分布情况,杨祥生等[13]基于Jensen模型提出一种新的工程尾流模型——Park-Gauss模型.该模型假设尾流区呈线性扩张,膨胀速率为k,尾流区径向风速呈高斯对称分布,如图4所示,其主要通过以下两步实现:
当我们悉心倾听一个人的幽幽诉说,当我们沉醉于慷慨激昂的演讲,当我们倾诉自己真实的心灵,当我们复述一个幽默的故事,当我们聚在一起夸夸其谈一个观点,当我们描述一个人的形象,当我们索要今天的晚报,当我们随意看到一个新颖的广告或标语,当我们醉心于时尚杂志的动听词汇,这些都离不开语文。

(4)

(5)
式中,r为径向上距离风轮中心的距离;rx为风力机下游位置处的尾流半径;u为风轮平面上的风速.
2.2 实测结果及分析
Taylor等[14-15]结合丹麦Nibe风电场在风力机运行期间的实测数据,对风场的尾流特性进行了研究,通过研究得到风力机下游4D和6D(D为叶轮直径)处的轮毂中心线延长线处的风速垂直廓线如图5虚线所示.而随着风电事业的不断发展,现有的参考数据[16]已不能满足高度上需求,于是根据74#风塔与73#风塔实测数据进行以下分析:分别采用10 min平均风速和瞬时风速对风场数据处理得到80 m高度处风速的变化情况,得到风速恢复比分布如图5所示,10 min时距下风力机下游5D处的风速恢复比集中在0.8~1.1区间,平均值与中位值基本重合,都小于1,对比45 m高度处恢复比有明显增大;瞬时风速下风速恢复比分布范围扩大,均值大于1,表明风速较来流风速有明显增大趋势.因此,在风电场施工布置时应充分考虑远尾流场对风塔不同高度处风速的影响,并且对现有的风速垂直廓线模型在高度上进行延伸,为以后更大型风力机的布置提供参考.

(a) 10 min平均风速恢复比曲线

(b) 瞬时风速恢复比曲线
结合风电场实测数据,通过计算得到74#风塔平均湍流强度为0.21,基于FFA风洞试验的尾流模型计算,根据式α=3Imean/4+0.01(Imean为湍流强度的平均值)进行线性外推,选取常数α(或尾流下降系数k)的合适取值为0.17,进而得到修正后的Jensen模型和Park-Gauss模型计算结果.将计算结果与实验值对比分析发现(见图6),无论是10 min平均风速还是瞬时风速,实测值的均值和中值都高于理论值,可见现有的尾流模型还不能直接应用于实际工程,应该结合多风向多尾流作用对下游风机的影响,提出更加符合实际的远场尾流模型.

(a) 10 min平均风速恢复比
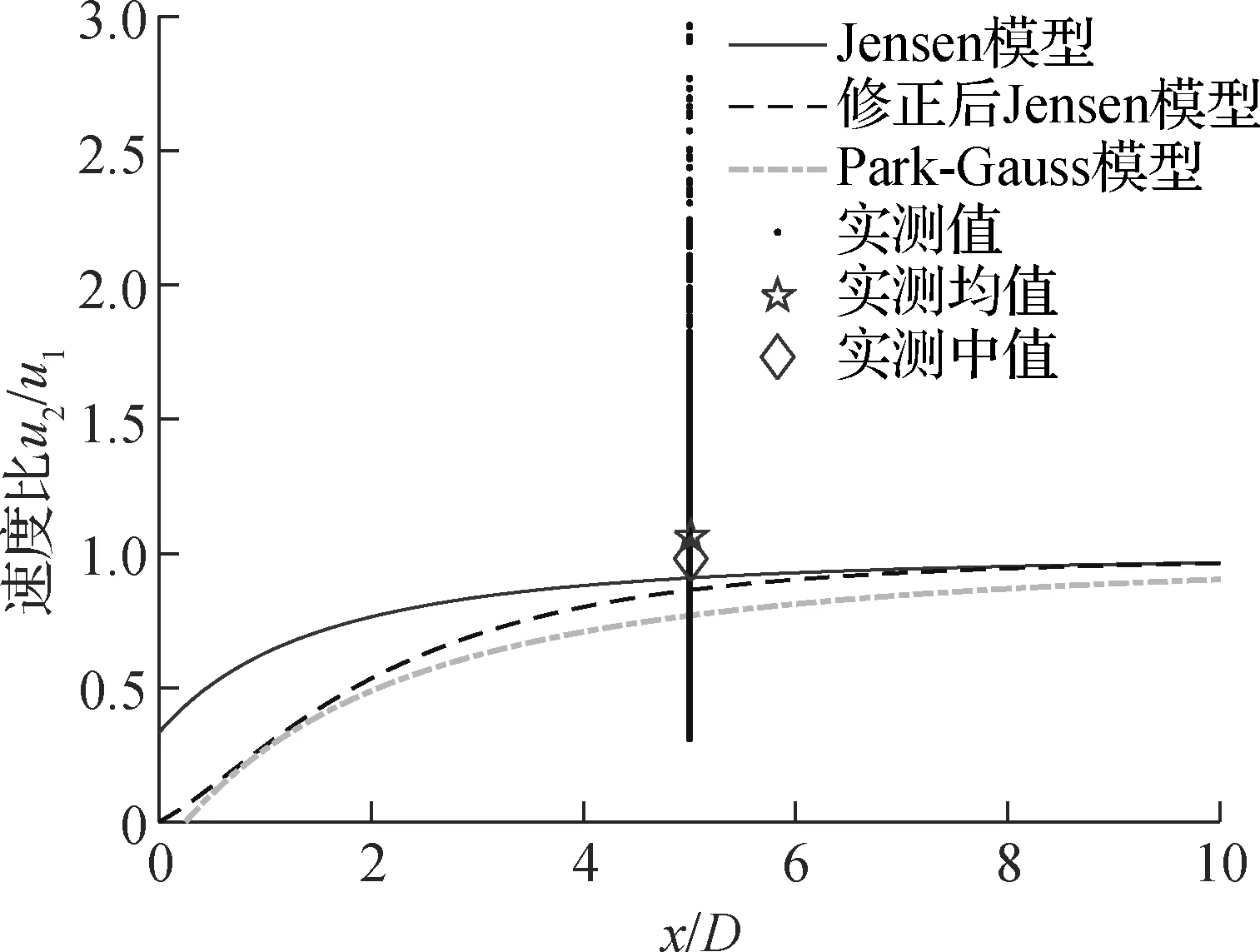
(b) 瞬时风速恢复比
图6 模型计算结果与实测值对比
3 基于实测数据的尾流作用下风场特性分析
3.1 实测风速风向对比
以大风天气下74#风塔和64#风塔的风速风向监测数据为研究对象,对该风场的风速分布情况进行分析.图7给出了观测期间风速风向对比图.由图可见,风速多出现在N,NNE,NNW三个方向,主导风向为正北方向,且风向分布较为集中;各风塔的风速波动幅度较大,瞬时风速在4~30 m/s范围内上下波动,大体上无明显差异;但从峰值上可看出,越靠近内部的风塔风速峰值越大.从全天变化趋势看,早上09:00之前风速总体较小,低于全天平均风速,之后风速开始增大,呈短周期大幅度波动状态,且在02:00左右,风速短时间内突然增大,然后又降到平衡位置,历经时间较短,这种突变作用可能会引起风电结构的风致振动响应增大,在设计施工时应予以重视.

(a) 风速风向分布图

(b) 74#瞬时风速时程
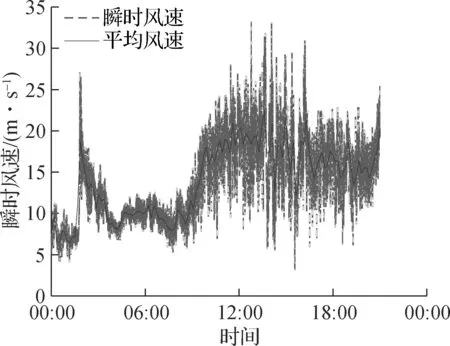
(c) 64#瞬时风速时程
图7 观测期间风速风向对比图
3.2 实测湍流特性对比
3.2.1 湍流强度
湍流强度是描述风速随时间和空间变化的程度,定义为10 min平均时距内脉动风速标准差与平均风速的比值,即
I=σ/U
(6)
式中,I为湍流强度;U为10 min时距内平均风速;σ为脉动风速标准差.该参数主要用以表征瞬时风速偏离平均风速的程度,风速波动越剧烈,湍流强度越大,风机承受载荷也会相应增大.
同一坐标位置的脉动风速标准差变化幅度通常小于平均风速的变化幅度,因此平均风速越大时湍流强度越低,而针对观测期间大风天气下的湍流强度实测结果发现(见图8(a)),湍流强度多分布在0.1~0.2之间,当风速大于10 m/s时,各个风塔总体都是随平均风速的增长大致呈增大趋势,且74#风塔湍流强度随平均风速的增大趋势略快于内部风塔.由图8(b)可知,随着时间的变化,各风塔湍流强度变化趋势呈倒“S”型,并且在大风时段09:00—18:00,发现湍流强度有逐渐升高的趋势,这会给风力机带来严重的载荷负担.
由图8(c)对比发现,内部风塔湍流强度更加集中于低湍流段,其中69#风塔低湍流特性更强,表明风力机的远尾流场作用可能会使湍流强度减小,并且由于多个尾流的叠加作用,各风机湍流强度的变化程度存在一定差异.

(a) 实测湍流强度与平均风速关系曲线

(b) 实测湍流强度随时间的变化

(c) 各风塔湍流强度分布图
图8 观测期间各风塔湍流强度对比图
3.2.2 湍流积分尺度
湍流积分尺度是脉动风中湍流涡旋平均尺度的量度,可反映脉动风速的空间相关性.基于Taylor假设,直接采用自相关函数直接积分的方法计算脉动风速的湍流积分尺度[17],即
(7)
式中,R(τ)为脉动风速的自相关函数.
图9(a)、图9(b)分别给出了湍流积分尺度随平均风速、时间的变化情况.通过对比分析可看出,各风塔的湍流积分尺度在大小上基本一致,就湍流积分尺度随平均风速、时间的变化情况而言,湍流积分尺度随着平均风速的增长有增大趋势,并且74#风塔随着平均风速的增长速率较内部风塔有所下降,而随着时间的推移湍流积分尺度虽然也在增大,但增长趋势却比较微弱.由图9(c)可看出,各风塔湍流积分尺度的分布情况都随着湍流积分尺度的增大呈阶梯式下降,并且不同取值区间的概率分布也无明显差异.
图10给出了各风塔湍流积分尺度随湍流强度的变化情况,可看出湍流强度与湍流积分尺度具有一定的正相关性,并且在远尾流场叠加作用下,内部风塔的湍流积分尺度随湍流强度的增长趋势更加明显.

(a) 实测湍流积分尺度与平均风速曲线

(b) 实测湍流积分尺度随时间的变化
(c) 各风塔湍流积分尺度分布图
图9 观测期间各风塔湍流积分尺度对比图

图10 湍流积分尺度与湍流强度关系图
4 实测风速概率分布特性对比
基于Abramovich射流理论将风轮后尾流区分为3个区域[18],该风场主导风向上的风机布置间距为5D,下游风机位于远尾流影响区域.根据实测数据,风场内湍流强度较大,平均值约为0.11,风力机近尾流区速度恢复较快.且从图11可看出,各风塔风速时程曲线基本上在5~25 m/s范围内上下波动,且平均风速都接近17 m/s,表明下游风机基本不受上游风机机械湍流影响,风速已大致恢复来流状态.

(a) 74#风塔瞬时风速时程
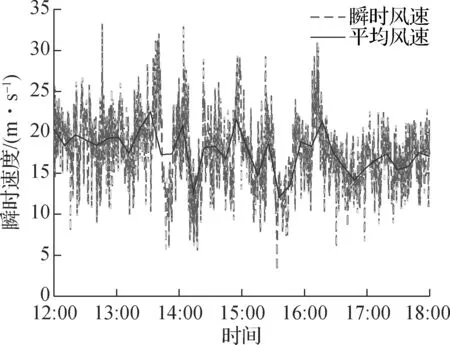
(b) 64#风塔瞬时风速时程
图12给出了各风塔实测风速概率密度对比情况,图中Vt为瞬时风速值,Vm为整段时程的平均风速,σ为瞬时风速标准差,用(Vt-Vm)/σ对瞬时风速进行标准化处理,如果实测风速近似满足高斯分布,则标准化处理后接近标准正态分布.此处用峰态系数和偏态系数作为评判标准,峰态系数反映风速分布峰部的尖峭程度,正态分布的峰度为3,偏态系数用于度量样本数据偏离某分布的情况,正态分布的偏度为0.

图12 各风塔风速概率密度分布对比图
由表1可见,74#风塔的偏态系数和峰态系数分别为-0.094和2.91,其数值都接近正态分布的取值,而64#风塔概率密度曲线在0.00左侧下凹趋势较明显,69#风塔峰态系数和偏态系数较大,表明实测风速在均值附近分布更加集中,左侧的离散性比右侧的强.总体上,风场外部实测风速更加符合高斯分布,可见内部风塔的风速虽然大致恢复到来流风速,但受到多个远尾流场的叠加效应,仍然存在一定程度上的差异.

表1 大风时段各风塔参数汇总
5 结论
1) 观测期间大风天气下,主导风向上风向分布较为集中,各塔的风速分布情况总体趋势一致,同时在大风时段均呈短周期大幅波动.
2) 当风速大于10 m/s时,外围风塔湍流强度随平均风速的增大速率略快于内部风塔湍流强度.湍流强度与湍流积分尺度有一定的正相关性,并且在远尾流场作用下,内部风塔的增长趋势更加明显.
3) 从各风塔的风速分布情况来看,下游风机基本不受上游风机机械湍流影响,而受到远尾流场作用,外围风塔更加接近高斯分布.
4) 修正后的Jensen模型和Park-Gauss模型与实际工程中多个尾流作用下的风电场尾流特性不太相符,多个风向上多个远尾流场的叠加作用还需要进一步探讨研究,并且需要对风电场尾流区的风速恢复比垂直廓线作出改进.

