WRF气象模式在高海拔复杂山地风电场中的应用研究
郁永静,刘志远,熊万能
(中国电建集团成都勘测设计研究院有限公司,四川成都610072)
0 引 言
风能资源评估是风能开发利用的关键环节,它是制定风能规划、风电场选址和风电功率预测的重要基础[1]。对于无测风或测风塔代表性不足区域的风能资源评估,目前行业内主要依赖于中尺度再分析MERRA数据[2]。但对于高海拔复杂山地风电场区域,由于MERRA数据精度较低,存在与实际测风数据误差较大、相关性差、风速分布不一致等问题,不能客观反映目标区域风能资源分布的真实情况,导致项目前期风能资源评估存在严重误判的风险。
为提高无测风或测风塔代表性不足区域复杂地形风电场风能资源评估的精度,本文将WRF气象模式应用于我国西南地区某高海拔山地风电场的数值模拟,并将模拟结果与区域内6座测风塔的实测数据和MERRA数据分别进行对比。分析年内风速分布、日内风速分布,并计算误差及相关性,研究WRF模拟对无测风或测风塔代表性不足区域复杂地形风电场风能资源评估的适用性。
1 WRF气象模式
WRF(Weather Research and Forecasting)气象模式是由美国环境预测中心(NCEP)、美国国家大气研究中心(NCAR)等科研机构开发的气象数值模式,WRF模式主要考虑1~10 km的大气运动模型,垂直方向采用气压地形追随坐标系统,网格系统为Arakawa C,并支持多重网格嵌套,能方便定位地理位置;时间积分采用三阶或四阶的龙格-库塔算法。模式包含12种微物理过程、5种积云对流参数化方案、4种陆面过程、3种表面边界层以及行星边界层、大气辐射等方案[3],用户可根据实际分辨率要求、天气状况、陆面条件等自由选择各种参数化方案组合。
2 模拟方案
本次模拟采用3重网格嵌套,第一到三重的网格区域范围见图1,输入地形分辨率分别为:10′、2′、30″,积分时间步长为18 s,各层模拟的空间分辨率分别为27、9、3 km,时间分辨率分别为:6、1、1 h,模拟2015年11月1日~2016年10月31日一个完整年的气象场。

图1 WRF模式三重嵌套网格区域示意

图2 测风塔地理位置示意

塔号塔高/m测风周期高程/m数据完整率/%1802015.09~2016.092 78395.652802015.10至今3 34496.443802015.11~2017.012 23294.814802015.10至今3 11595.765802015.10至今2 70194.466802015.04~2017.072 62093.65
备注:数据完整率是指2015年10月1日到2016年9月30日之间的数据完整率
模拟区域内某风电场共设立了6座测风塔,海拔最高的2号测风塔和海拔最低的3号测风塔高差为1 112 m,地形极其复杂,测风塔基本情况见表1。为验证模拟效果,本文通过WRF的后处理模块,提取6座测风塔位置处的逐小时WRF模拟数据;整理了6座测风塔的实测数据;通过商用软件下载了6座测风塔位置的MERRA数据[4]。各测风塔地理位置见图2。
3 模拟效果验证
3.1 结果对比分析
6座测风塔测风代表年各月平均风速与WRF模拟结果、MERRA80 m高度月平均风速统计见表2。选取数据完整率最高的2号测风塔作为代表测风塔绘制各类分布图[5],2号测风塔80 m高度实测、WRF模拟和MERRA年内风速分布见图3。

图3 2号测风塔80 m高度实测、WRF模拟和MERRA年内风速分布
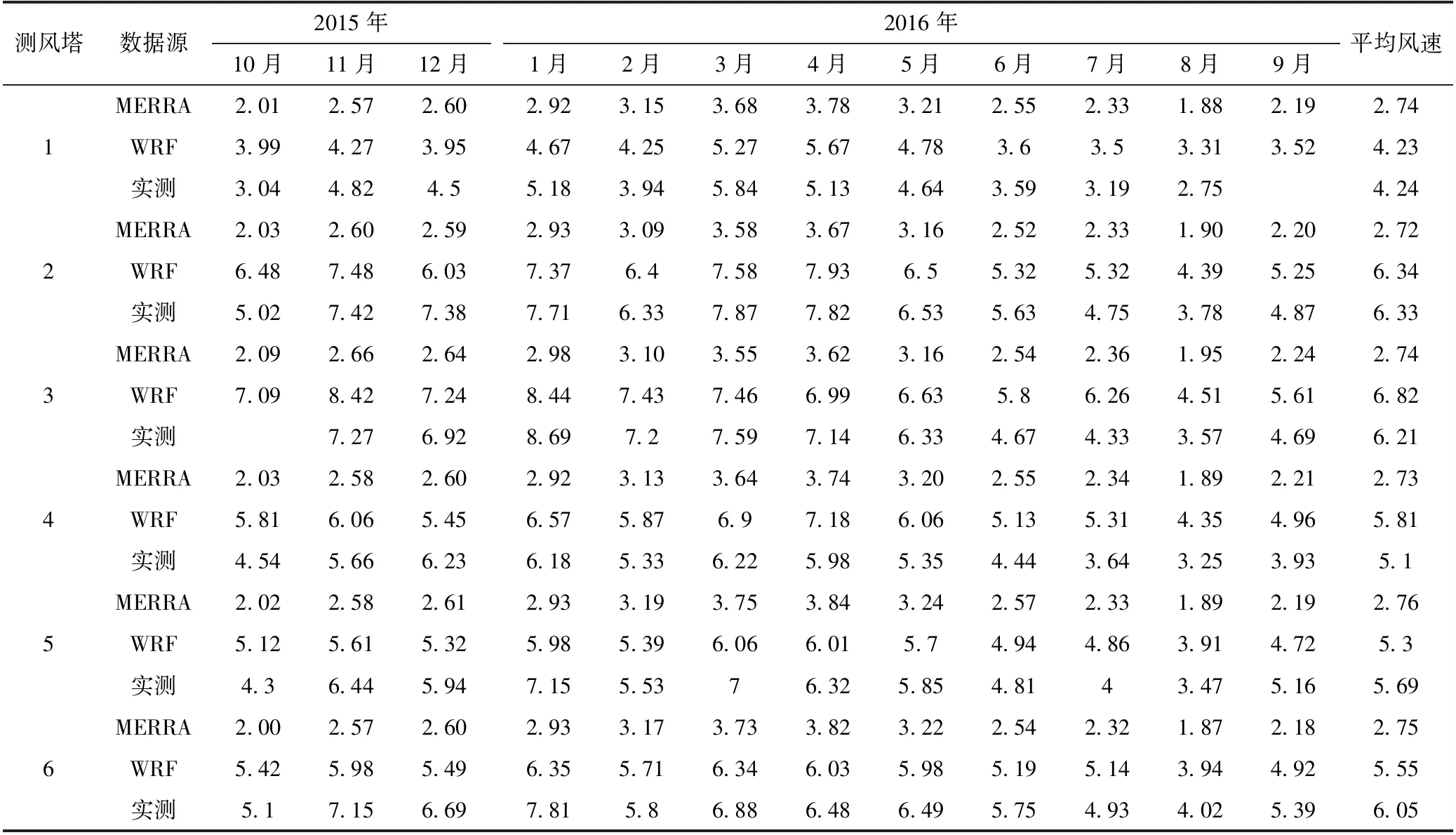
m/s
由图表可知,年内各月WRF风速和实测风速变化基本一致:WRF最大风速月为4月,风速为7.93 m/s;实测风速最大风速月为3月,风速为7.87 m/s;MERRA最大风速月为4月,风速为3.67 m/s;WRF、实测和MERRA最小风速月为8月,风速值分别为4.39、 3.78、1.9 m/s。WRF、MERRA与实测数据的年内风速分布趋势均具有较高的一致性,但MERRA数据明显偏低。
3.2 误差分析
鉴于风速数据存在0风速时段,不采用相对误差来评价模拟效果。本文采用平均绝对误差[6](RMSE)对模拟效果进行评价,其表达式为
(1)

年平均风速误差为年平均风速绝对误差的均值,因为仅分析一个完整年的数据,n值取1;月平均风速误差为各月平均风速绝对误差的均值,n值取12;日平均风速误差为各日平均风速绝对误差的均值,因2016年为闰年,n值取366。
各测风塔月实测风速与模拟风速绝对误差见表3。各测风塔WRF模拟与实测数据的年、月、日平均风速绝对误差均低于MERRA,6座测风塔实测与WRF模拟年平均风速误差均值为0.37 m/s,与MERRA年平均风速误差均值为2.86 m/s,WRF模拟具有较高的模拟精度。
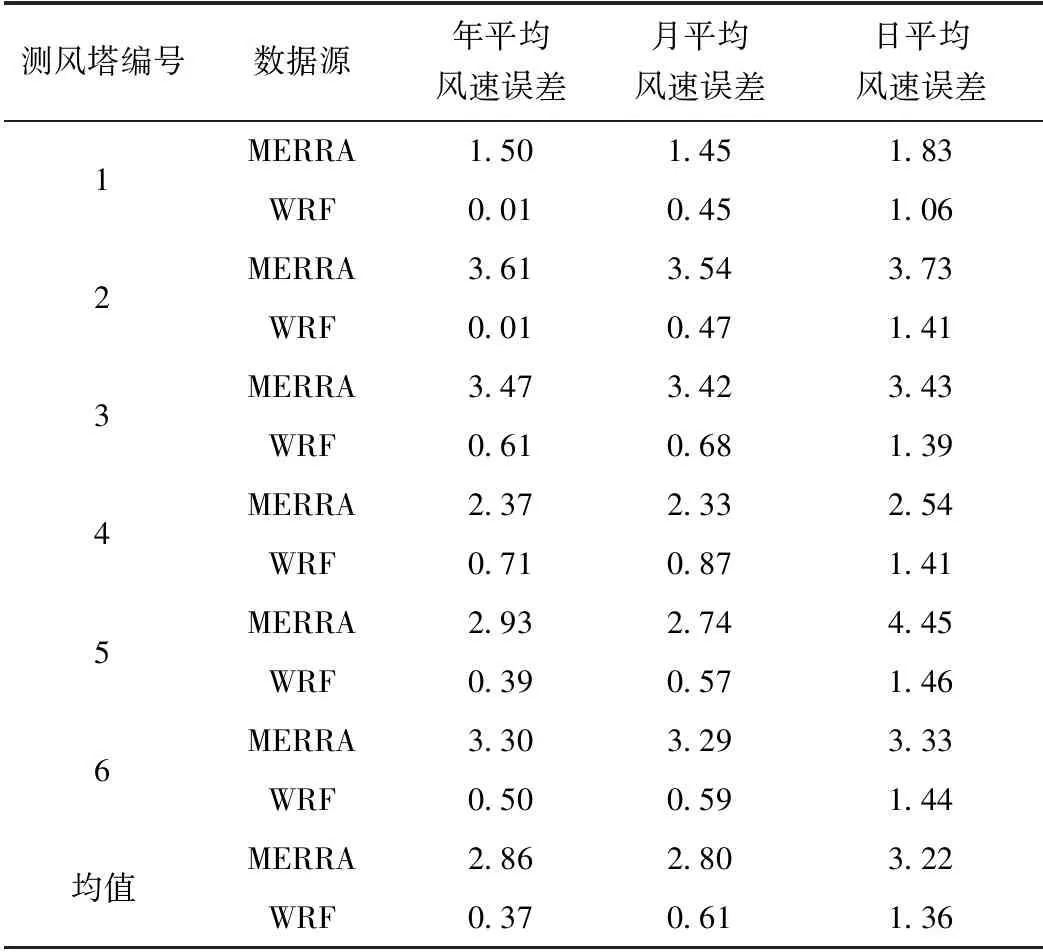
表3 模拟、MERRA与实测80 m高度年、月、日平均风速绝对误差 m/s
3.3 相关性分析
对各测风塔实测与WRF、实测与MERRA日平均风速进行相关性分析[7],相关系数见表4,相关性分布见图4。各测风塔WRF模拟与实测数据的相关系数均高于MERRA,6座测风塔实测与WRF模拟月平均风速的相关系数均值为0.7095,与MERRA月平均风速的相关系数均值为0.5759,WRF模拟数据较MERRA数据具有明显优势,可更好应用于测风塔缺测数据插补。
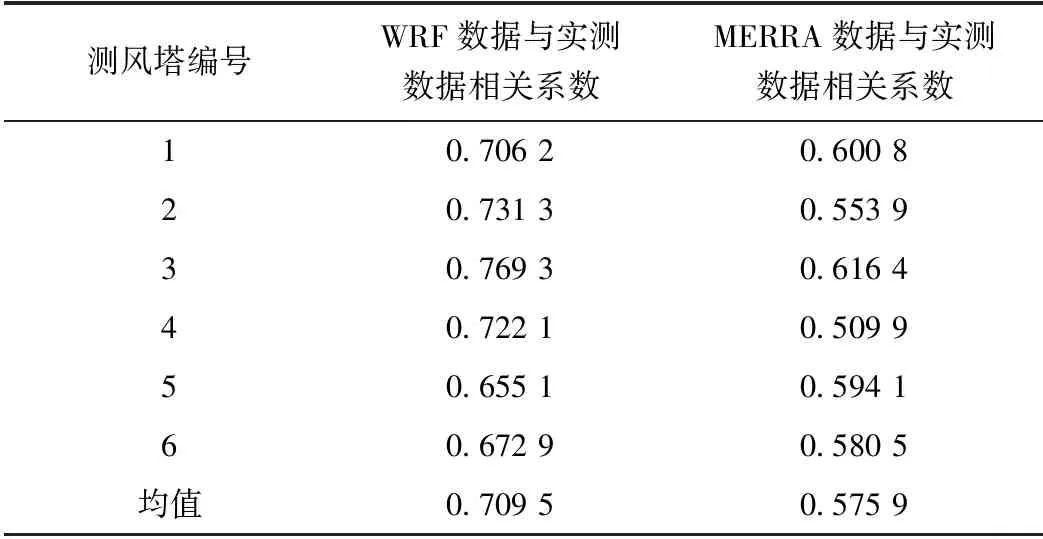
表4 各测风塔模拟、MERRA与实测数据相关系数

图4 2号测风塔80 m高度WRF模拟、MERRA与实测日平均风速相关性分布
4 结 论
针对6座测风塔,分别应用WRF模拟和MERRA提取了测风塔位置一个完整年的逐小时风速,并与实测数据进行对比分析,得出如下结论:
(1)WRF模拟数据与实测数据的年内及日内风速分布趋势具有较高的一致性,且明显优于MERRA数据。
(2)WRF模拟具有较高的模拟精度,6座测风WRF模拟年、月、日平均风速绝对误差均值为0.37、0.61、1.36 m/s;6座测风塔实测与WRF模拟日平均风速的相关系数均值为0.709 5。
(3)WRF模拟数据基本上可用于高海拔复杂地形无测风塔地区及测风塔代表性不足区域的风能资源评估,WRF模拟的普遍适应性研究还有待进一步深化。

