梁端约束条件对箱形梁剪力滞效应的影响

张玉元 张元海 张 慧

(兰州交通大学土木工程学院, 兰州 730070)

薄壁箱梁发生竖向挠曲变形时，由于面内剪切变形使得远离腹板的翼板区域翘曲程度大，靠近腹板的翼板区域翘曲程度小，从而在截面上产生一种应力不均匀的现象，这就是剪力滞效应．

Reissner[1]针对双轴对称的矩形箱梁，首次采用三次抛物线为剪力滞翘曲位移函数，运用能量变分法建立了剪力滞效应分析理论，并导出了箱形梁挠度和纵向应力的解析解．张元海等[2-3]通过建立箱梁翼缘板面内剪切变形与纵向位移的关系，从理论上证明了二次抛物线是较为合理的翘曲位移函数形式．此外，现有诸多文献采用余弦函数为翘曲位移函数[4-5]，余弦函数可按无穷级数展开成若干个多项式，其中包含了二次抛物线、三次抛物线等，在计算精度方面余弦函数也是较为合适的翘曲位移函数．在剪力滞翘曲广义位移方面，Reissner[1]首次提出最大剪切转角差为广义位移，并在剪力滞效应研究领域得到了广泛应用，但采用同一最大剪切转角差并不能准确反映各板的翘曲位移．为了考虑各板纵向翘曲位移的差异，选取不同的最大剪切转角差为广义位移[5-6]，这样能更精确地反映剪力滞翘曲变形，但最大剪切转角差不具有明确的物理意义，且不便于工程人员理解和使用．杨绿峰等[7-8]选取剪力滞效应引起的附加挠度为广义位移，显然，这样的广义位移物理意义明确，且便于工程技术人员使用．在翘曲位移模式修正方面，钱寅泉等[4]应用能量变分法导出了各板的翘曲位移函数修正系数，同时对翘曲位移模式加入均匀附加位移项，并通过翘曲应力轴向自平衡条件求得此附加位移．此后，这种修正思路在国内外得到了广泛的推广和应用[9-14]，但是当翼缘板宽与顶板半宽相等时，此修正系数失效，为解决此问题，张元海等[15]针对悬臂板翘曲位移函数引入边界约束修正系数，以反映悬臂板与顶板不同边界约束对剪力滞翘曲位移模式的影响．此修正方法虽然能够真实反映悬臂板和顶板的翘曲应力分布，但不能客观反映底板的翘曲应力状态，舒小娟等[16]提出箱形梁剪力滞翘曲变形中性轴与初等梁弯曲变形中性轴位置存在差异，重新定义了翘曲变形中性轴的坐标位置，运用此方法计算的截面翘曲应力横向分布能客观反映翘曲变形的本质．

以三跨连续刚构箱梁桥为例，边跨和中跨可近似认为是一端固定另一端简支的箱梁和两端固定的箱梁，两端简支的约束情况即是工程中常见的简支箱梁桥．可见，研究梁端约束条件对剪力滞效应的影响具有一定的工程意义．本文在剪力滞翘曲位移模式中引入弯翘中性轴修正系数、翘曲应力自平衡修正系数和悬臂板边界约束修正系数，选取剪力滞效应引起的附加挠度为广义位移，运用能量变分法建立不同梁端约束条件下剪力滞系数和附加挠度的解析解，通过数值算例揭示梁端约束条件对剪力滞效应的影响规律．

1 剪力滞翘曲变形状态分析

图1为竖向分布荷载q(z)作用下发生挠曲变形的箱梁简图，坐标系xoyz和x′o′y′z分别用于研究初等梁弯曲变形和剪力滞翘曲变形，其中o和o′分别位于截面形心处和翘曲变形中性轴处．箱梁的变形状态可分为初等梁弯曲变形状态和剪力滞翘曲变形状态，其中初等梁弯曲变形状态分析已在材料力学中解决，下面只分析剪力滞翘曲变形状态．在剪力滞翘曲变形状态下，箱梁横截面上任一点处的纵向翘曲位移uω(x,y,z)可表达为

(1)

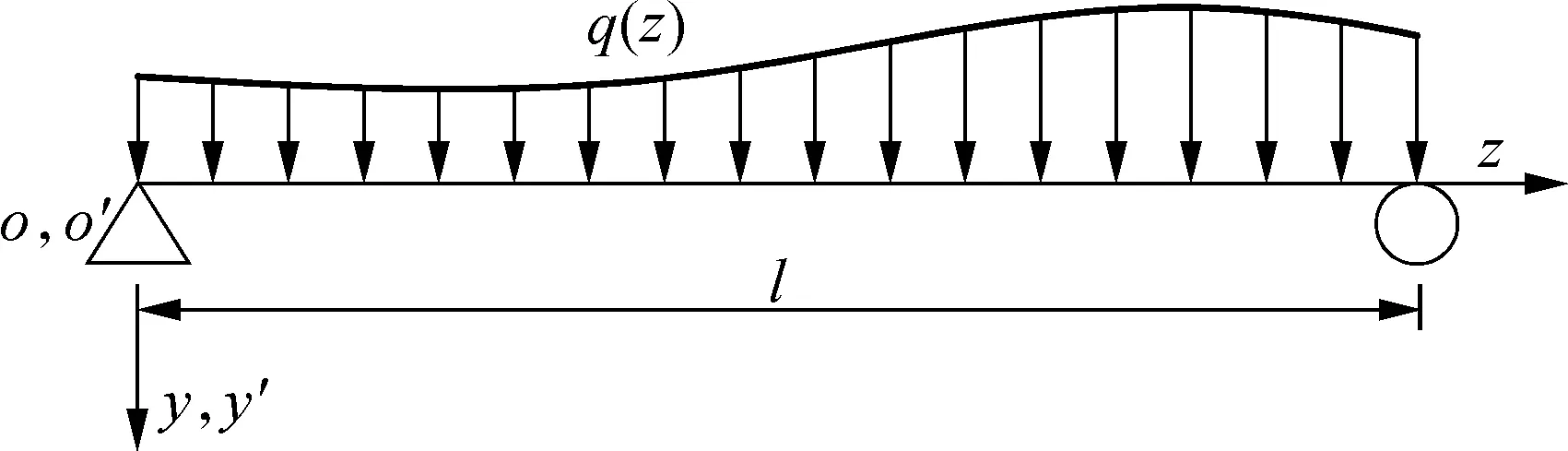
(a) 坐标系及荷载

(b) 横截面

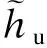
(2)

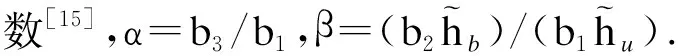
根据几何方程及胡克定律，由式(1)可得箱梁横截面任一点处的翘曲应力σω(x,y,z)为

(3)

箱梁发生剪力滞翘曲变形时，截面翘曲应力满足自平衡条件，即翘曲应力在面内不合成轴力和弯矩，则有

(4)

(5)

将式(3)分别代入式(4)和式(5)，可得

(6)

(7)

经积分运算可得

(8)

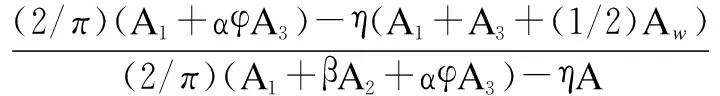
(9)

与式(3)中剪力滞翘曲应力σω(x,y,z)相对应的广义力矩Mω定义为[15]

(10)

式中,Iζ称为剪力滞翘曲惯性矩,即

(11)

将式(3)和式(10)整理可得翘曲应力σω的另一表达式[15]:

(12)

据此可给出箱梁截面任一点处的剪力滞系数λ的表达式:

(13)

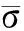
2 控制微分方程及边界条件

由弹性力学可知,箱梁的翘曲应变能可表达为

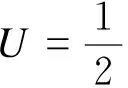
(14)

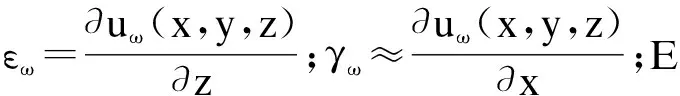
箱梁翘曲正应变εω相应的应变能可表达为

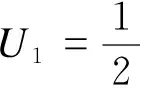
(15)

箱梁翘曲剪应变γω相应的应变能可表达为

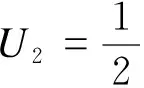
(16)

式中

外力势能为

(17)

则箱梁的剪力滞翘曲变形总势能可表达为

(18)

对总势能泛函进行一阶变分运算,并令δΠ=0,化简可得关于附加挠度的控制微分方程:

(19)

式中,k为Reissner参数[15],即

(20)

方程(19)为一个四阶常系数非齐次线性微分方程,其通解的一般形式为

f=C1+C2z+C3sinh(kz)+C4cosh(kz)+f*

(21)

式中的待定系数由边界条件求解,f*为仅与q(z)分布有关的特解.当箱梁受均布荷载q作用时,其特解可表达为

确定上述4个常数的边界条件为

固定端

f=0,f′=0

简支端

f=0,f″=0

自由端

f″=0,f‴-k2f′=0

3 附加挠度及剪力滞系数的求解

如图2所示,简支箱梁受均布荷载q作用时,箱梁的剪力滞附加挠度可表达为

(22)

为确定式(22)中的4个参数,需利用以下边界条件:f(0)=0,f″(0)=0,f(l)=0,f″(l)=0.

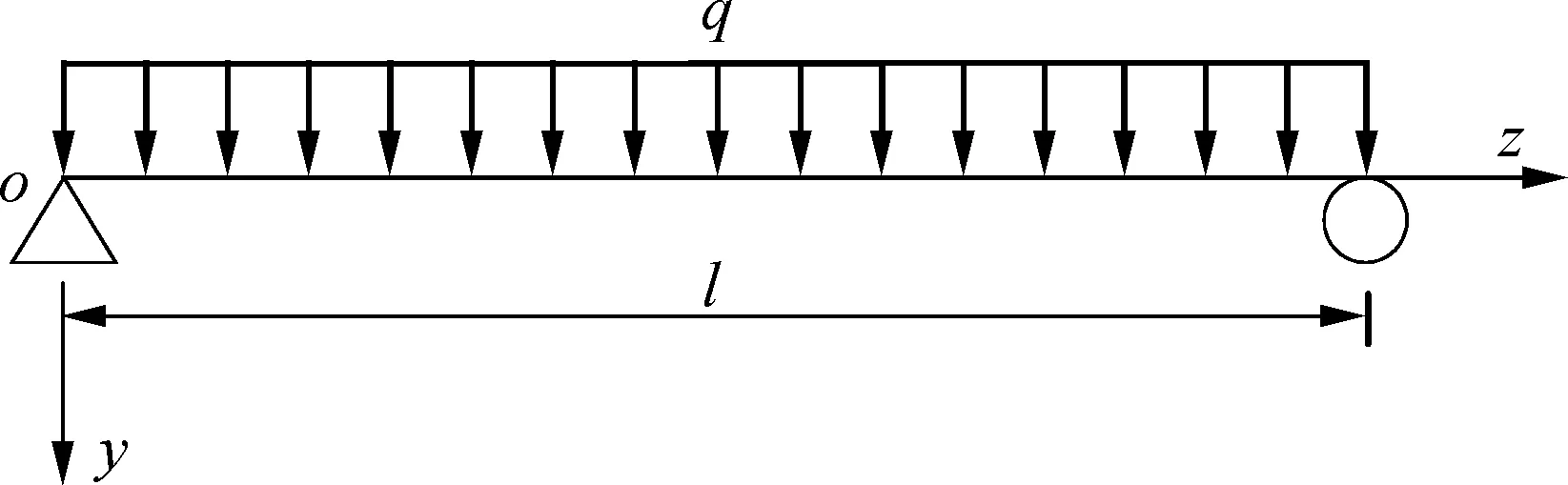
图2 简支箱梁受均布荷载作用

利用以上4个边界条件确定常数C1～C4后,即可得到简支箱梁剪力滞附加挠度的计算公式:

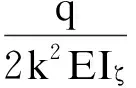
(23)

将附加挠度表达式相继代入式(10)和式(13),即可得到简支箱梁横截面任一点处的剪力滞系数计算公式:

(24)

如图3所示,一端固定另一端简支的箱梁受均布荷载q作用时,其剪力滞附加挠度的表达式与简支箱梁相同,如式(22)所示.

图3 一端固定另一端简支的箱梁受均布荷载作用

为确定该箱梁剪力滞附加挠度表达式中的4个参数,需利用以下边界条件:f(0)=0,f′(0)=0,f(l)=0,f″(l)=0.

利用以上4个边界条件确定常数C1～C4后,即可得到一端固定另一端简支的箱梁剪力滞附加挠度计算公式:

(25)

将附加挠度表达式相继代入式(10)和式(13),即可得到一端固定另一端简支的箱梁横截面任一点处的剪力滞系数计算公式:

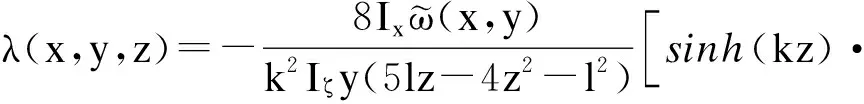
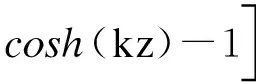
(26)

如图4所示,两端固定的箱梁受均布荷载q作用时,其剪力滞附加挠度的表达式与简支箱梁相同,即式(22).

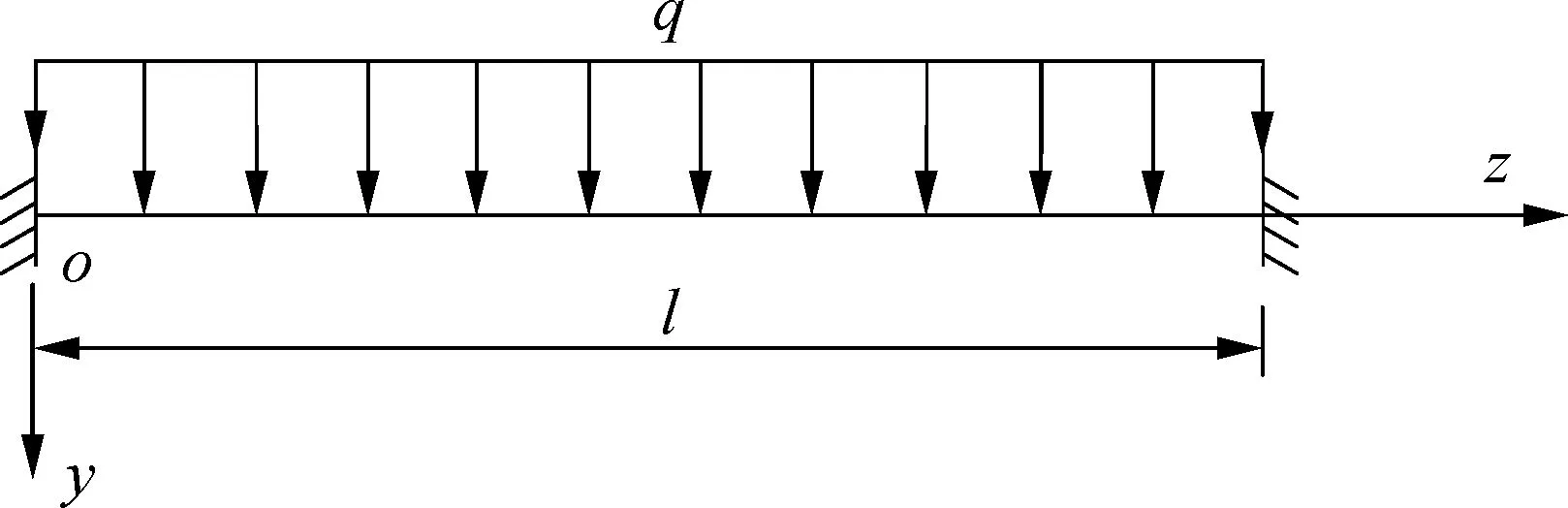
图4 两端固定的箱梁受均布荷载作用

为了确定该箱梁剪力滞附加挠度表达式中的4个参数,需利用以下边界条件:f(0)=0,f′(0)=0,f(l)=0,f′(l)=0.

利用4个边界条件确定常数C1～C4后,即可得到两端固定的箱梁剪力滞附加挠度计算公式:

(27)

将附加挠度表达式相继代入式(10)和式(13),即可得到两端固定的箱梁横截面任一点处的剪力滞系数计算公式:

(28)

4 算例分析

以文献[17]中跨度为0.8 m的箱梁模型为例,截面尺寸如图5所示,材料弹性模量为3 GPa,泊松比为0.385,在跨间作用均布荷载,其荷载集度q=10 kN/m.按照本文方法算得:hu=27.7 mm,hb=

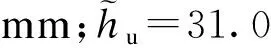
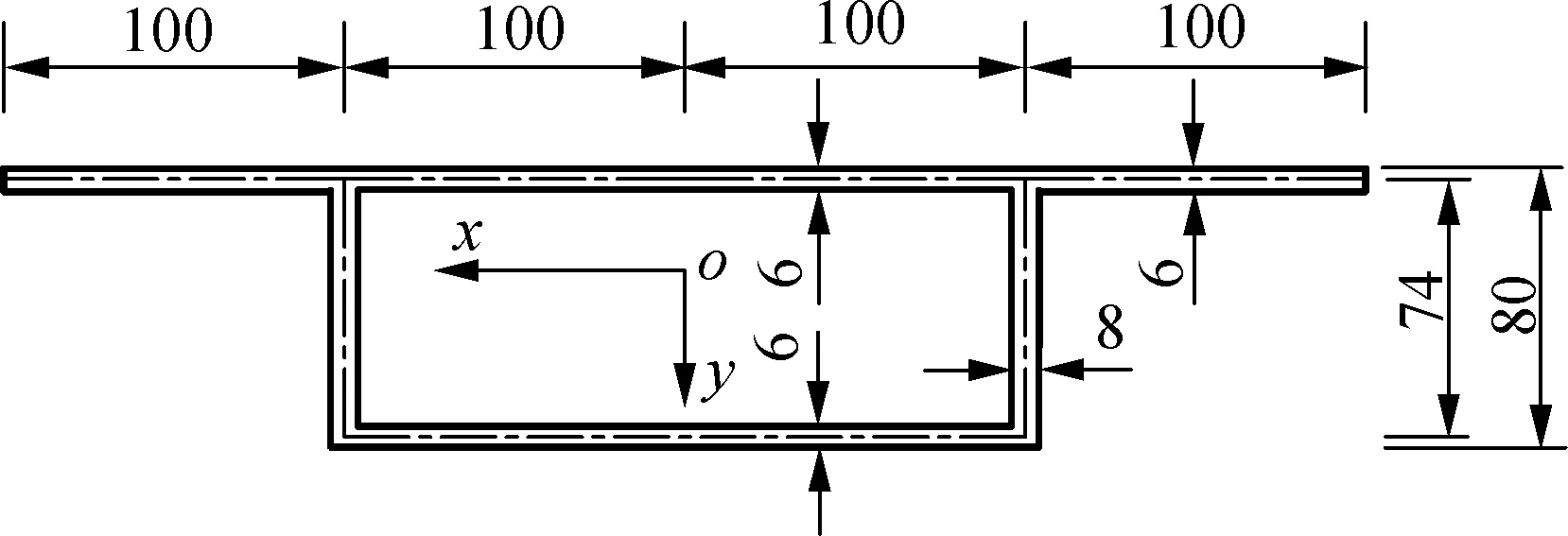
图5 箱梁模型横截面尺寸(单位:mm)

为了验证本文方法的正确性,以图5给出的箱梁模型为例,借助有限元ANSYS软件中的shell63单元,对该箱梁模型进行有限元数值分析,共划分为6 422个节点,6 400个单元,计算得到简支箱梁(SS箱梁)、一端固定另一端简支的箱梁(FS箱梁)和两端固定的箱梁(FF箱梁)跨中截面计算点的剪力滞系数.然后利用本文方法计算得到相应点的剪力滞系数,将以上结果列于表1,以便比较.

表1 跨中截面计算点的剪力滞系数比较

表1给出了不同梁端约束条件下箱梁跨中截面计算点的剪力滞系数本文解和ANSYS解.显然,二者吻合程度良好,进而验证了本文方法的正确性.

为了研究梁端约束条件对剪力滞效应的影响,以图5给出的箱梁模型为例,在梁端约束条件变化时,保持跨度、截面尺寸及荷载不变.利用本文公式计算不同梁端约束条件下箱梁相应截面的剪力滞系数和附加挠度,绘制跨中截面剪力滞系数横向分布图、关键点剪力滞系数纵向分布图和附加挠度分布图,如图6～图8所示,并将截面关键点的剪力滞系数和附加挠度列于表2和表3,以便对比.

图6给出了不同梁端约束条件下箱梁跨中截面剪力滞系数的横向分布曲线,可看出两端固定的箱梁剪力滞系数横向分布曲线较陡峭,简支箱梁剪力滞系数横向分布曲线较平缓,一端固定另一端简支的箱梁剪力滞系数横向分布曲线介于二者之间.由此可见,梁端约束程度越强,剪力滞系数横向分布曲线越陡峭.

表2给出了不同梁端约束条件下箱梁跨中截面关键点的剪力滞系数比较,可看出与简支箱梁相比,一端固定另一端简支的箱梁和两端固定的箱梁在顶板与腹板交汇处的剪力滞系数分别增大了12.86%和25.63%,底板与腹板交汇处的剪力滞系数分别增大了10.93%和21.87%,顶板中点处的剪力滞系数分别减小了5.83%和11.65%,底板中点处的剪力滞系数分别减小了12.51和25.03%,悬臂板端部的剪力滞系数分别减小了15.89%和31.67%.

(a)上翼板

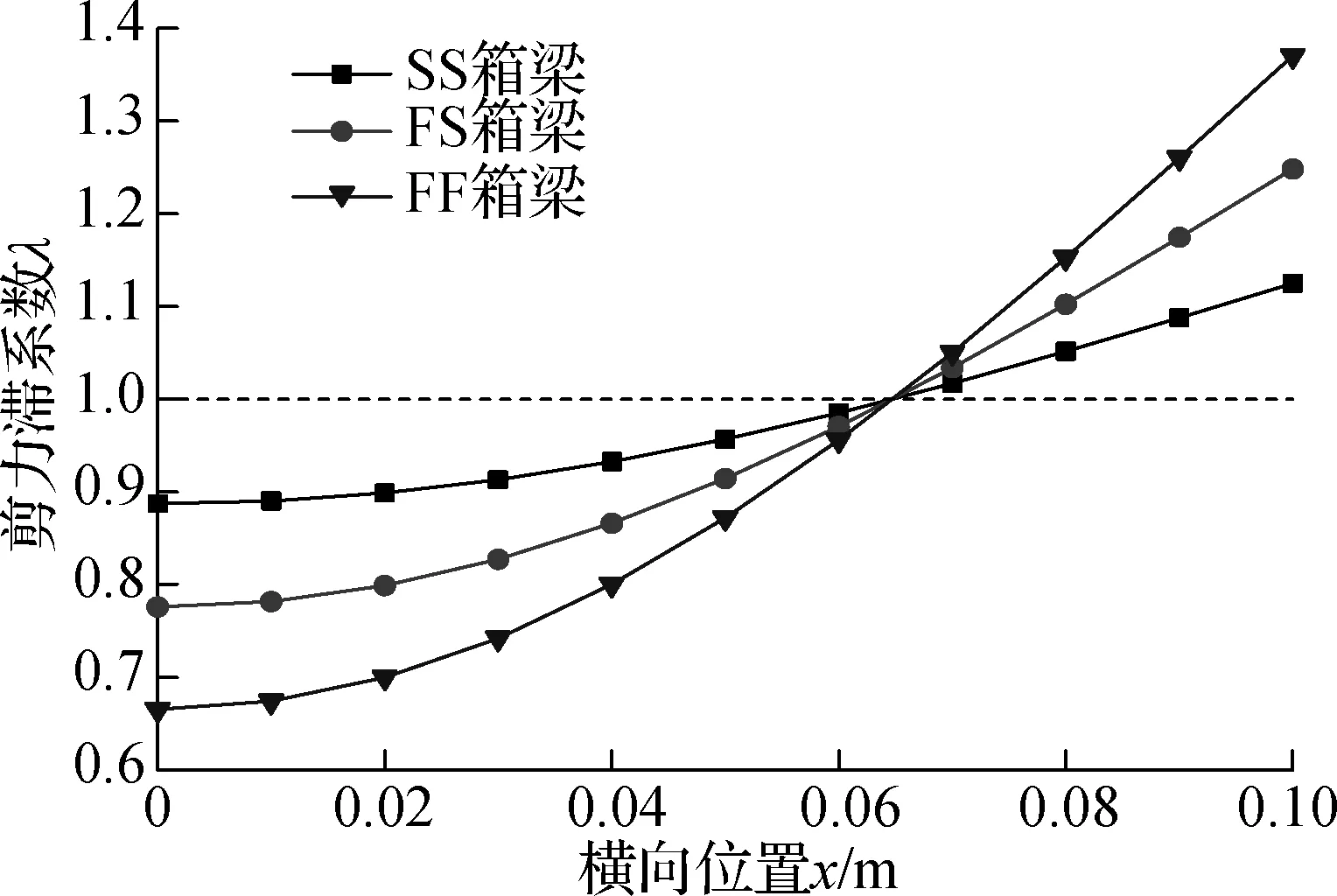
(b) 底板

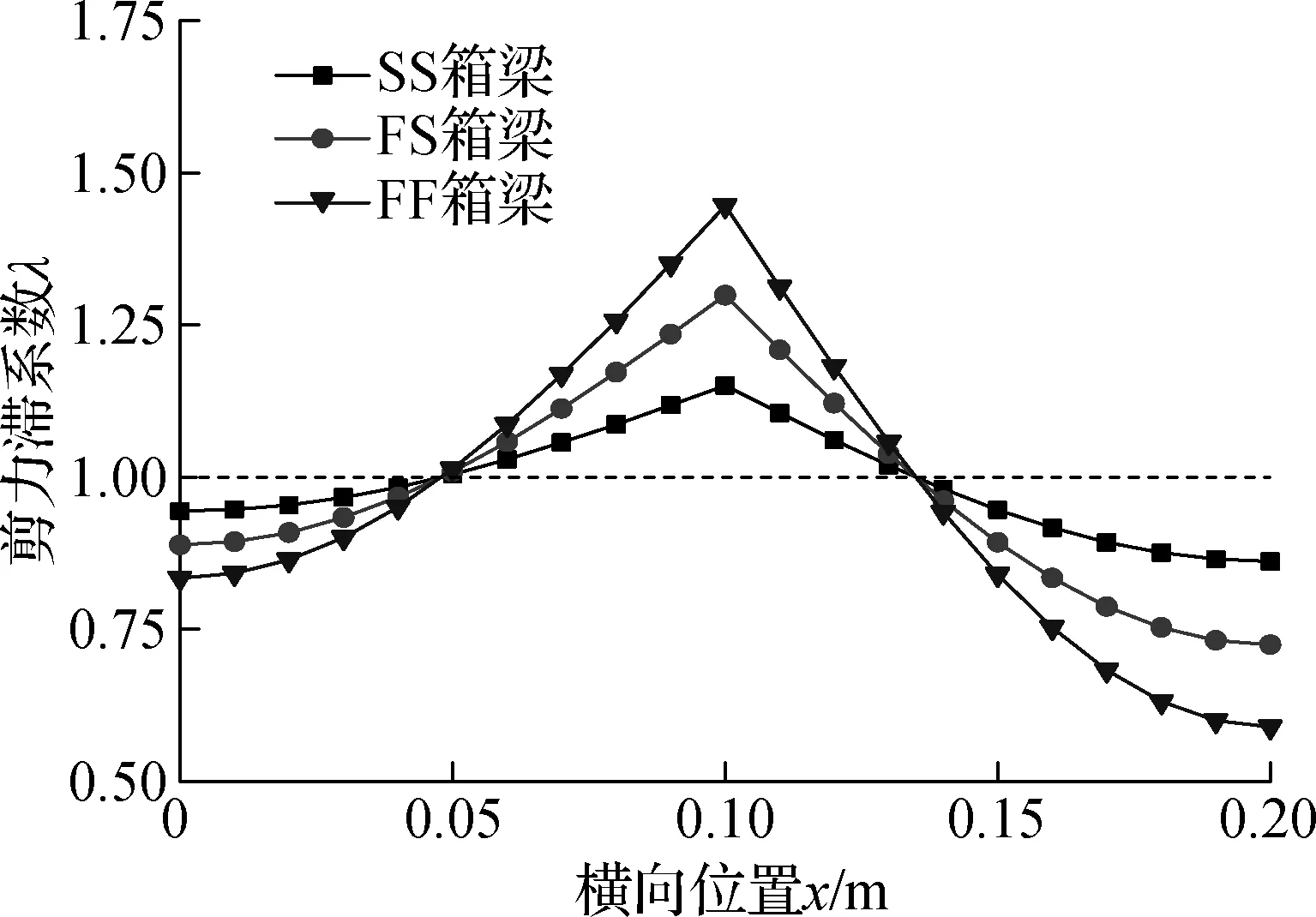
图7 顶板与腹板交汇处的剪力滞系数纵向分布

横向位置x/mmSS箱梁FS箱梁差值比δ1/%FF箱梁差值比δ2/% 上翼板00.9440.889-5.830.834-11.651001.1511.29912.861.44625.632000.8620.725-15.890.589-31.67底板00.8870.776-12.510.665-25.031001.1251.24810.931.37121.87注:δ1,δ2分别为FS箱梁和FF箱梁的剪力滞系数与SS箱梁剪力滞系数的相对误差比.

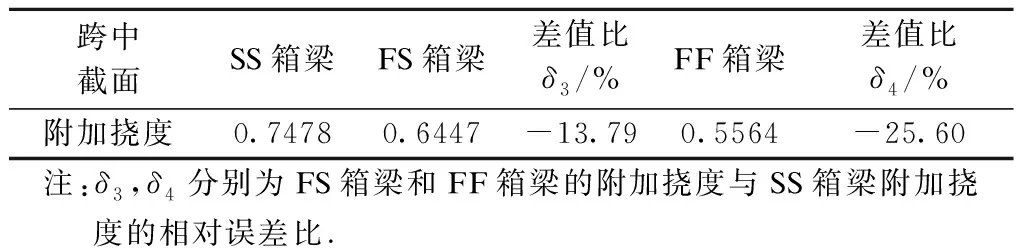
表3 跨中截面剪力滞附加挠度比较 mm

图7给出了不同梁端约束条件下箱梁顶板与腹板交汇处的剪力滞系数纵向分布曲线,可看出简支箱梁剪力滞系数沿纵向连续分布,一端固定另一端简支的箱梁和两端固定的箱梁剪力滞系数纵向分布在反弯点处发生突变,在反弯点两侧的正、负弯矩区内,剪力滞系数纵向分布与简支箱梁和悬臂箱梁分布规律类似.显然,梁端约束程度越强,剪力滞系数纵向分布曲线越陡峭.与一端固定另一端简支的箱梁相比,两端固定的箱梁在固定端和跨中截面,顶板与腹板交汇处的剪力滞系数分别增大了19.31%和11.34%.图8给出了不同梁端约束条件下箱梁附加挠度的变化曲线,可看出简支箱梁附加挠度最大,两端固定的箱梁附加挠度最小,一端固定另一端简支的箱梁附加挠度介于二者之间.由此可见,梁端约束条件越强,附加挠度越小;附加挠度的峰值向两端约束较弱的一端移动.

表3给出了不同梁端约束条件下箱梁跨中截面的附加挠度比较.从表中可看出,与简支箱梁相比,一端固定另一端简支的箱梁和两端固定的箱梁跨中截面的附加挠度分别减小了13.79%和25.60%.

本文以等截面箱梁为例研究梁端约束条件对剪力滞效应的影响,所采用的研究方法及导出的计算公式同样适用于变截面连续箱梁,因此运用有限梁段法可实现梁端约束条件对变截面箱梁剪力滞效应影响的研究.

5 结论

1) 本文运用能量变分法建立了不同梁端约束条件下箱梁的剪力滞系数和附加挠度解析解,算例计算表明,本文计算结果与有限元数值解吻合良好,进而验证了本文方法的正确性.

2) 梁端约束程度越强,剪力滞系数横向分布曲线越陡峭.与简支箱梁相比,一端固定另一端简支的箱梁和两端固定的箱梁顶板与腹板交汇处的剪力滞系数分别增大了12.86%和25.63%.

3) 梁端约束程度越强,剪力滞系数纵向分布曲线越陡峭.正、负弯矩区的剪力滞系数纵向分布规律与相应的简支箱梁和悬臂箱梁类似;与一端固定另一端简支的箱梁相比,两端固定的箱梁跨中截面顶板与腹板交汇处的剪力滞系数增大了11.34%.

4) 梁端约束程度越强,剪力滞附加挠度纵向分布曲线越平缓.与简支箱梁相比,一端固定另一端简支的箱梁和两端固定的箱梁跨中截面附加挠度分别减小了13.79%和25.60%.