多级平行轴滚筒齿轮数学建模及动力学分析
黄晓冬 袁银男 欧阳天成 陈 南 潘明章
(1江苏大学汽车与交通工程学院, 镇江 212013)(2东南大学机械学院, 南京 211189)(3广西大学机械工程学院, 南宁 530004)
齿轮传动装置是现代机械装备的重要组成部分,随着旋转机械向高转速、大型化、集成化方向发展,对机械系统整机性能有重要影响的齿轮动力学已成为当前研究热点[1-2].对胶印机而言,良好的运行平稳性是印刷质量的重要保证,胶印印刷过程依靠多级平行轴滚筒齿轮的相互转动完成图像转移,传动过程中如何保证齿轮的高精度啮合是实现精确套印的前提.因此,滚筒齿轮啮合传动的平稳性和精确度是高速胶印机设计与制造的首要任务[2-4].
近年来,国内外众多学者对齿轮传动系统动力学问题展开了一系列研究[5-10],在传动误差与系统动态响应的关系、齿轮啮合非线性动力学、齿侧间隙与动态特性的关系等方面取得了丰富的研究成果.郭磊等[11]运用ADAMS软件建立汽车变速箱多体动力学模型,分析了多档位下的齿轮啮合拍击特性和啸叫噪声,并利用表面振动速度法对箱体振动速度等级进行精确识别.在考虑齿轮偏心、传动误差和时变输入/输出力矩前提下,任朝晖等[12]利用集中参数法建立风电斜齿轮传动动力学模型,分析了转速、轴承间隙等参数对系统动态响应的影响.Yang等[13-14]在考虑接触时变啮合刚度、齿侧间隙基础上,建立行星齿轮空间机械臂关节动力学模型,研究系统不同设计参数下的非线性动力学特性.Besharati等[15]通过建立包含非对称齿侧间隙的齿轮-齿条非线性动力学模型,研究了预紧载荷对系统动态响应的影响规律.为了研究齿侧间隙与啮合温度对齿轮-滑动轴承系统动力学特性的影响,Fargère等[16]整合齿轮-传动轴动力学模型和滑动轴承润滑模型,基于时间步长积分法与牛顿迭代法的联合求解获得控制方程数值解.基于有限元思想,Ouyang等[17]建立胶印机单对滚筒-轴承-齿轮非线性动力学模型,利用龙格库塔法求解控制方程并分析了转速、啮合刚度、齿侧间隙等因素对系统动态特性的影响.基于断裂力学原理,Han等[18]通过有限单元法建立了包含传动轴裂纹的平行轴齿轮动力学模型,分析了裂纹类型和参数对稳态、非稳态下系统动态特性的影响.
以上文献大都将焦点集中在传统的多级平行轴齿轮系统,但对胶印机平行轴齿轮传动系统动力学问题的研究却相当缺乏.实验测试结果显示,胶印机平行轴齿轮传动系统是高速印刷状态下的主要振源,也是决定整机平稳性的关键因素.因此,本文利用集中参数法建立胶印机平行轴滚筒齿轮多自由度非线性动力学模型,基于数值解分析系统的动态特性,为胶印机滚筒齿轮系统动态特性的改善提供理论支持和分析方法.
1 动力学模型
如图1所示,胶印机多级平行轴滚筒齿轮传动系统主要由齿轮、滚筒和轴承组成,在滚筒轴颈处设置轴承起支承作用.印刷过程中,齿轮1转动带动纸张从传纸滚筒传递到压印滚筒(沿X方向),油墨从印版滚筒转移到橡皮滚筒,橡皮滚筒将图像或文字转移到压印滚筒表面的纸张.振动过大将导致印品模糊,甚至出现卡纸现象.一般而言,振动强度随转速提高而增大,为了提高印刷效率,有必要研究胶印机平行轴滚筒齿轮的动态特性.
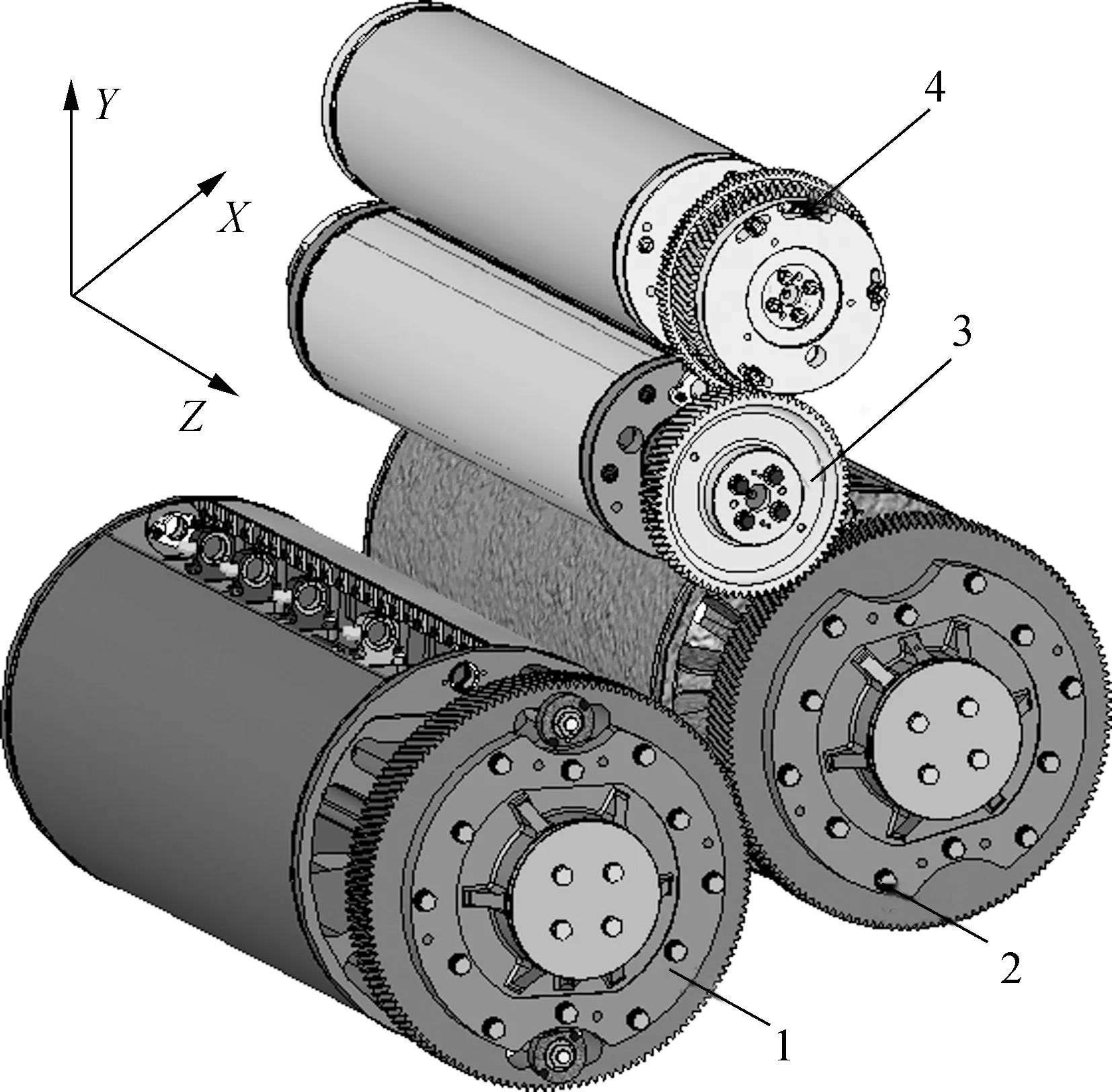
图1 胶印机多级平行轴滚筒齿轮传动系统三维图
基于振动理论,本研究利用集中参数法建立胶印机多级平行轴滚筒齿轮传动系统动力学模型.在保证计算精度前提下,对原机模型进行适当简化,利用动力学等效法将滚筒平动质量和转动惯量向斜齿轮中心简化,用时变刚度弹簧模拟齿轮啮合,支承轴承处理为等效刚度弹簧.
图2(a)中,每个斜齿轮具有3个平动自由度和1个旋转自由度,分别是X和Y方向的弯曲位移,Z方向的轴向位移和绕平行轴的扭转位移.该机构属于4级平行轴齿轮传动系统,共16个自由度,因此其动力学模型节点位移向量为
q= {x1,y1,z1,θ1,x2,y2,z2,θ2,
x3,y3,z3,θ3,x4,y4,z4,θ4}T
(1)
式中,xi(i=1,2,3,4)为斜齿轮沿X方向位移;yi(i=1,2,3,4)为斜齿轮沿Y方向位移;zi(i=1,2,3,4)为斜齿轮沿Z方向位移;θi(i=1,2,3,4)为斜齿轮绕Z方向的转角.
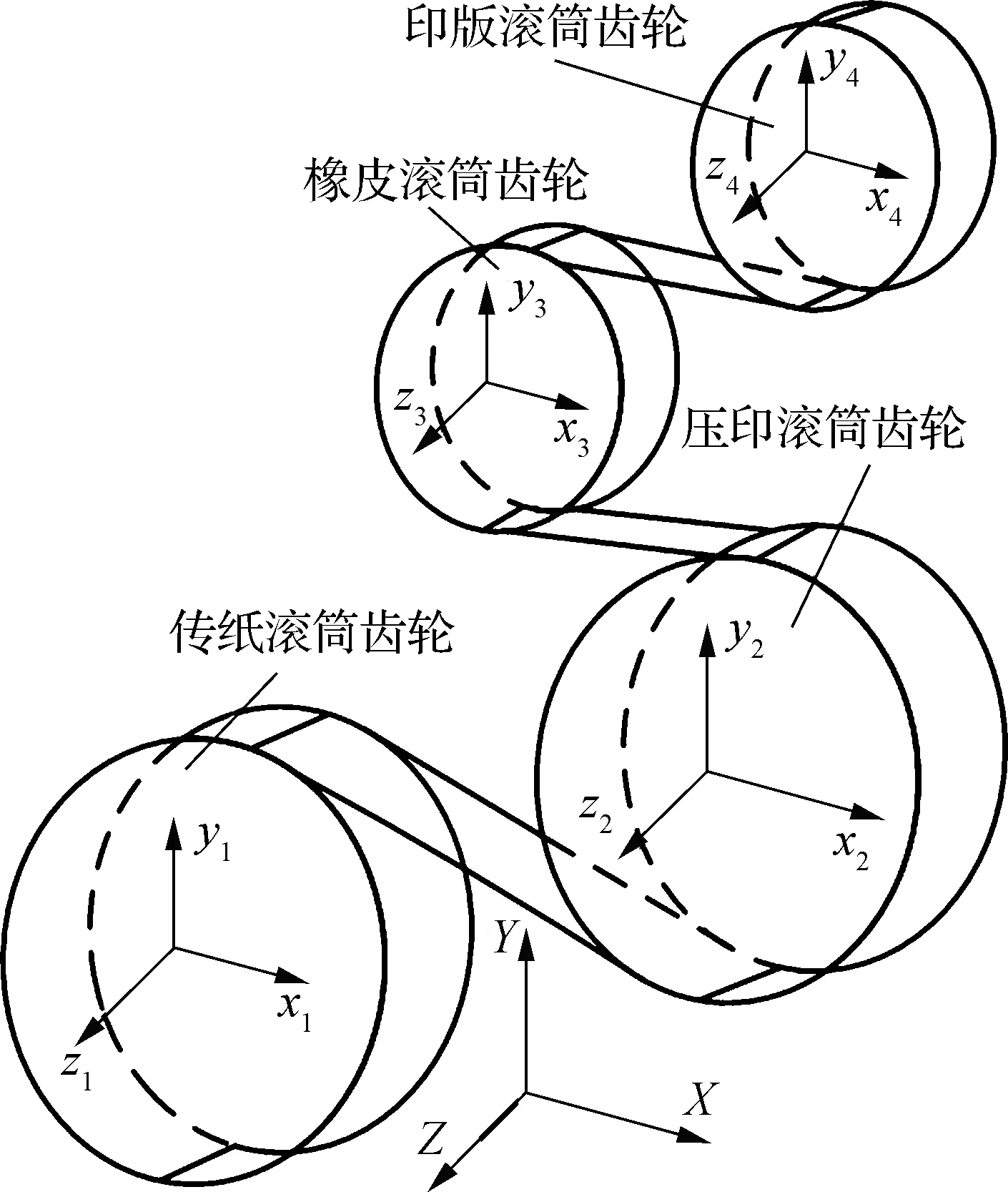
(a) 平行轴斜齿轮整体坐标系简图
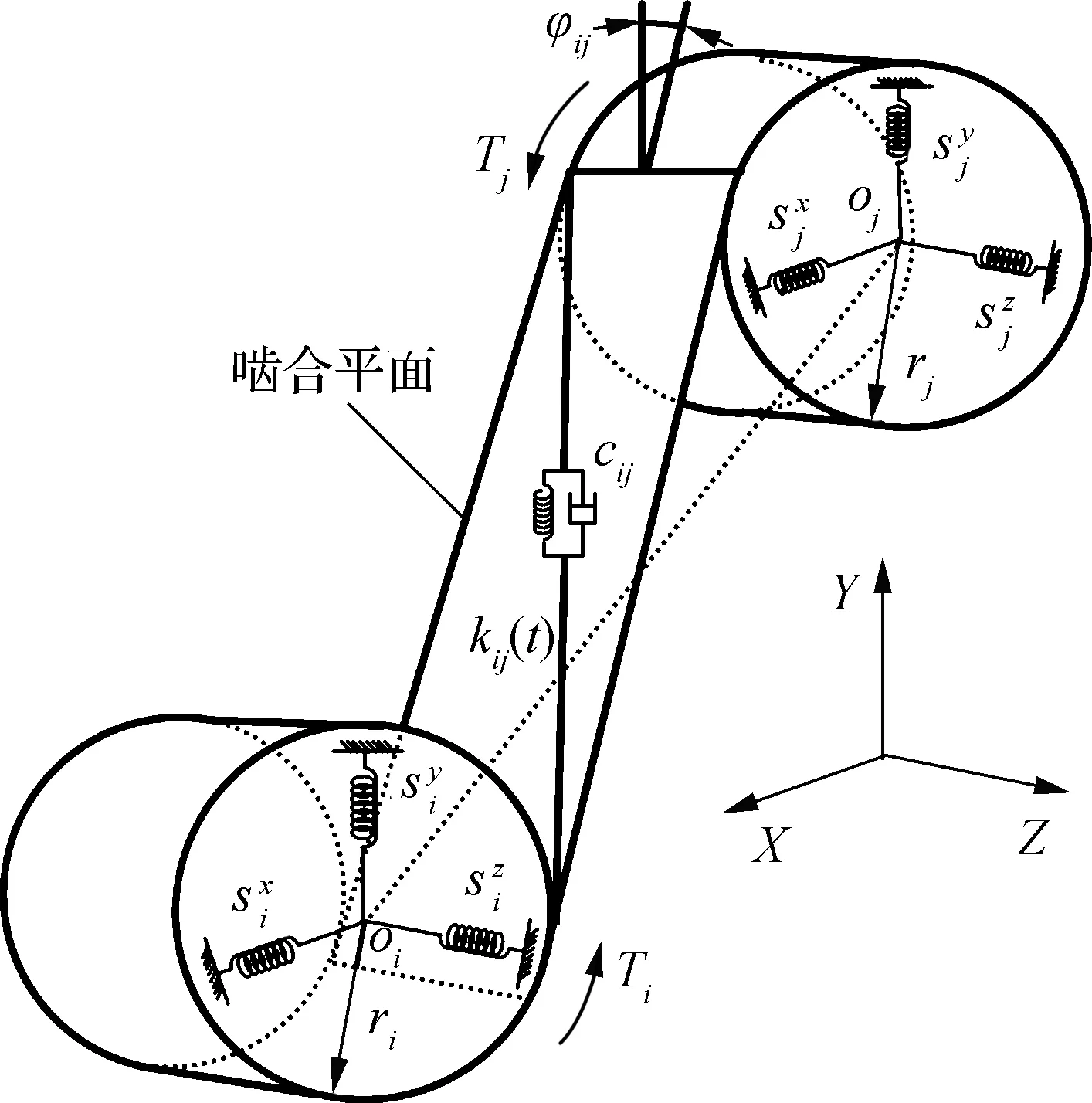
(b) 斜齿轮啮合副动力学模型
1.1 动态啮合力
如图2(b)所示,在外部驱动转矩和负载力矩共同作用下,接触齿面将产生弹性变形,接触点在啮合平面内发生相对位移,啮合点在接触面内的相对位移近似表达式为
(2)
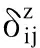
斜齿轮啮合副沿X,Y,Z方向的动态啮合力分别为
(3)
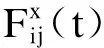
1.2 啮合刚度、啮合阻尼、静态传动误差
齿轮啮合过程中,由于接触轮齿对数、接触几何特征等因素的变化,导致啮合刚度具有时变特性,形成参数振动.基于回归分析法,Cai[19]提出了一种较为接近实验测量值的斜齿轮啮合刚度拟合公式,本文将采用该拟合公式来模拟多级平行轴滚筒斜齿轮的啮合刚度.单对轮齿的啮合刚度计算式为
(4)
式中,t为沿接触线的啮合时间;tz为一个节距的啮合周期时间;mn为斜齿轮法向模数;ε为总重合度;εa为端面重合度;kp为分度圆节点位置的啮合刚度;bc为齿宽;H为全齿高.
多级平行轴滚筒斜齿轮啮合刚度为
(5)
式中,n为同一时刻同时参与啮合的轮齿对数.
为了简化计算过程,本文采用与速度成正比的线性黏性阻尼模拟齿轮啮合阻尼,其计算式为
(6)
式中,Ji,Jj分别为主动轮和从动轮的转动惯量;kave为齿轮平均啮合刚度;ξg为齿轮啮合阻尼比(取ξg=0.05).
在静态条件下,由于制造原因引起的齿廓、齿向偏差以及轮齿接触变形而导致的啮合误差称为齿轮静态传动误差.考虑到静态传动误差具有周期性,其谐波函数表达式可描述为
(7)
式中,e0为静态传动误差平均值;en为静态传动误差谐波项幅值;νn为静态传动误差谐波项啮合相位;ωm为齿轮啮合频率,ωm=ωizi,其中ωi为主动轮转速,zi为主动轮齿数.
1.3 等效轴承刚度
胶印机采用滚动轴承支承斜齿轮平行轴,本文采用等效原理推导滚动轴承的等效刚度.在忽略轴承内、外滚道与钢球之间的间隙、轴承接触角不随载荷改变的前提下,轴承沿X,Y,Z方向的等效刚度分别为[20]
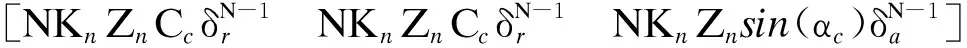
(8)
式中,sx为X方向的等效轴承刚度;sy为Y方向的等效轴承刚度;sz为Z方向的等效轴承刚度;δr为轴承内、外圈的径向相对位移;δa为轴承内、外圈的轴向相对位移;Kn为赫兹刚度系数;Zn为滚子数目;Cc为余弦计算系数;αc为接触角.
1.4 等效质量
确定X,Y,Z方向上的等效质量和轴承安装等效刚度是集中参数法建立平行轴滚筒齿轮动力学模型的重要环节.图3为胶印机单级滚筒齿轮等效参数简图,由于滚筒沿轴向的长度远大于齿轮中心(C点)到轴承2的距离(lb>la),因此将滚筒视为质量均匀分布的梁.胶印机滚筒在图3所示的支承方式下,梁单元(滚筒)任意一点的弹性变形为
(9)
且有
(10)式中,yC为梁单元在C点的弹性变形;Wg为外载荷;la为齿轮中心到轴承的距离;lb为滚筒长度;E为梁单元的弹性模量;I为梁单元的截面惯性矩.
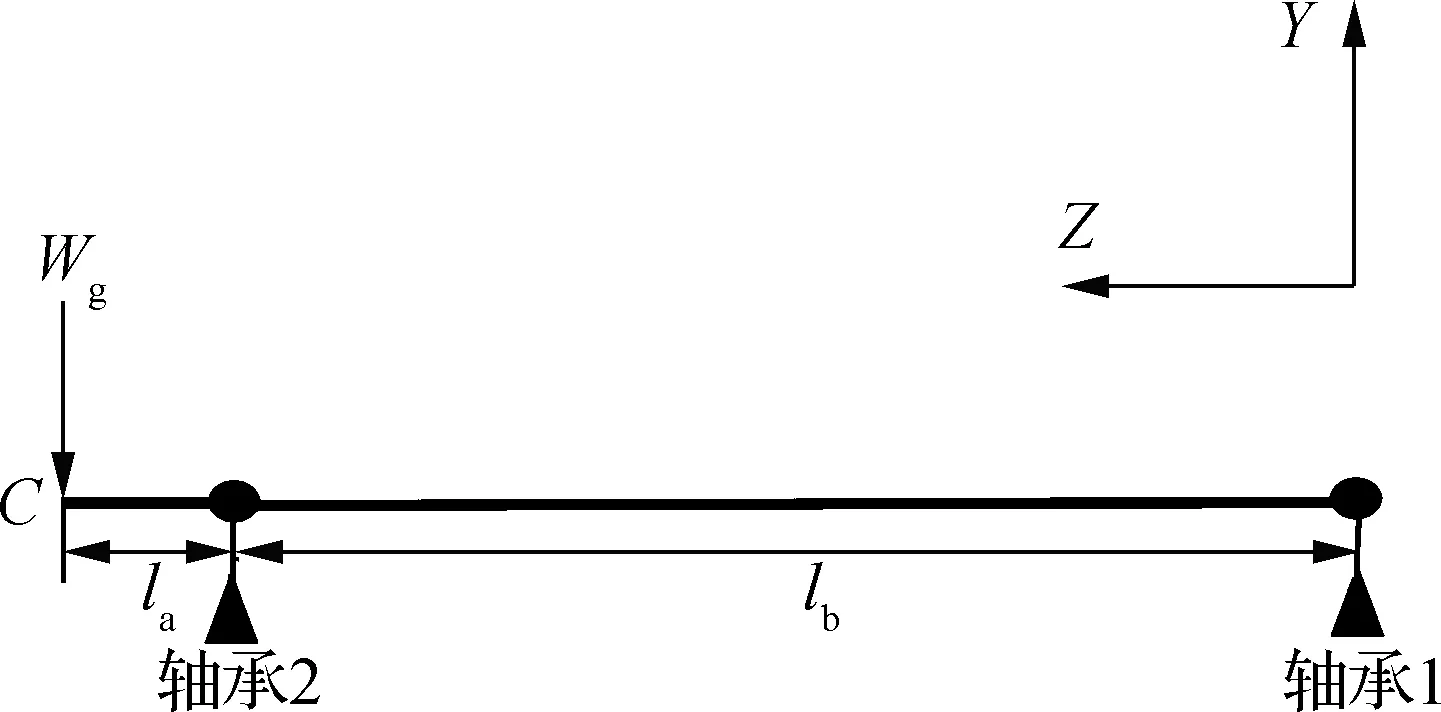
图3 等效参数简图
根据Rayleigh法原理[21],梁单元最大动能表达式为
(11)
式中,Kmax为梁单元的最大动能;wg为单位长度的梁单元质量;g为重力加速度.
基于动力学等效原理,平动方向和竖直方向的等效质量和轴承安装等效刚度分别为
(12)
式中,mx和my分别为平动方向和竖直方向上齿轮中心等效质量;mg为斜齿轮质量;mc为滚筒质量.
同样按照上述方法求得轴向振动方向齿轮中心等效质量和轴承安装等效刚度,表达式为
(13)
式中,mz为轴向方向的齿轮中心等效质量.
1.5 动力学方程
在任意时刻,滚筒斜齿轮上的惯性力、阻尼力和弹性力构成平衡力系,根据达朗贝尔原理得到每个滚筒斜齿轮的运动微分方程:
1) 传纸滚筒斜齿轮
(14a)
2) 压印滚筒斜齿轮
(14b)
3) 橡皮滚筒斜齿轮
(14c)
4) 印版滚筒斜齿轮
(14d)
将4个滚筒斜齿轮的偏微分方程整合并用矩阵形式表示,得到16个自由度的多级平行轴滚筒齿轮动力学方程,其表达式为

(15)
式中,M为滚筒齿轮质量矩阵;C为滚筒齿轮阻尼矩阵;K为滚筒齿轮刚度矩阵;F为滚筒齿轮载荷列向量;q为滚筒齿轮节点位移列向量.
2 动态特性分析
表1给出了胶印机平行轴滚筒齿轮传动系统的特征参数,表2给出了滚筒齿轮的部分啮合参数.
在转速4 000~17 000 r/h 范围内,本文采用Newmark-β法对胶印机平行轴滚筒齿轮动力学模型进行数值求解,分析系统的动态特性,如齿轮啮合力的波动、齿轮中心角速度的波动、齿轮中心加速度随转速的变化趋势,以及螺旋角、压力角与啮合刚度波动的关系.

表1 滚筒齿轮传动系统的特征参数

表2 齿轮啮合参数
2.1 动态啮合力
啮合力的波动是造成齿轮传动系统振动的最直接因素,波动越剧烈,动载系数越大,振动越强烈.为验证本文建立的多级平行轴滚筒齿轮动力学模型的准确性,图4将ADAMS模型[4]得到的啮合力与本文建立的动力学模型的数值计算啮合力作对比.从图4可看出,在17 000 r/h转速下,斜齿轮的啮合力具有周期性质,呈上下波动状态,齿对12的啮合力围绕9 000 N上下波动,而齿轮34的啮合力则围绕1 200 N上下波动.由图4可知,ADAMS模型的计算结果在波动幅值和波动变化率方面均大于动力学模型的数值解,原因是ADAMS模型通过定义刚体碰撞函数模拟齿轮啮合,而动力学模型则是基于振动理论建立控制方程,因此动力学模型的数值解呈现相对较小的波动性和波动变化率.通过图4的对比,验证了本文建立的动力学模型的计算精度.

(a) 齿对12
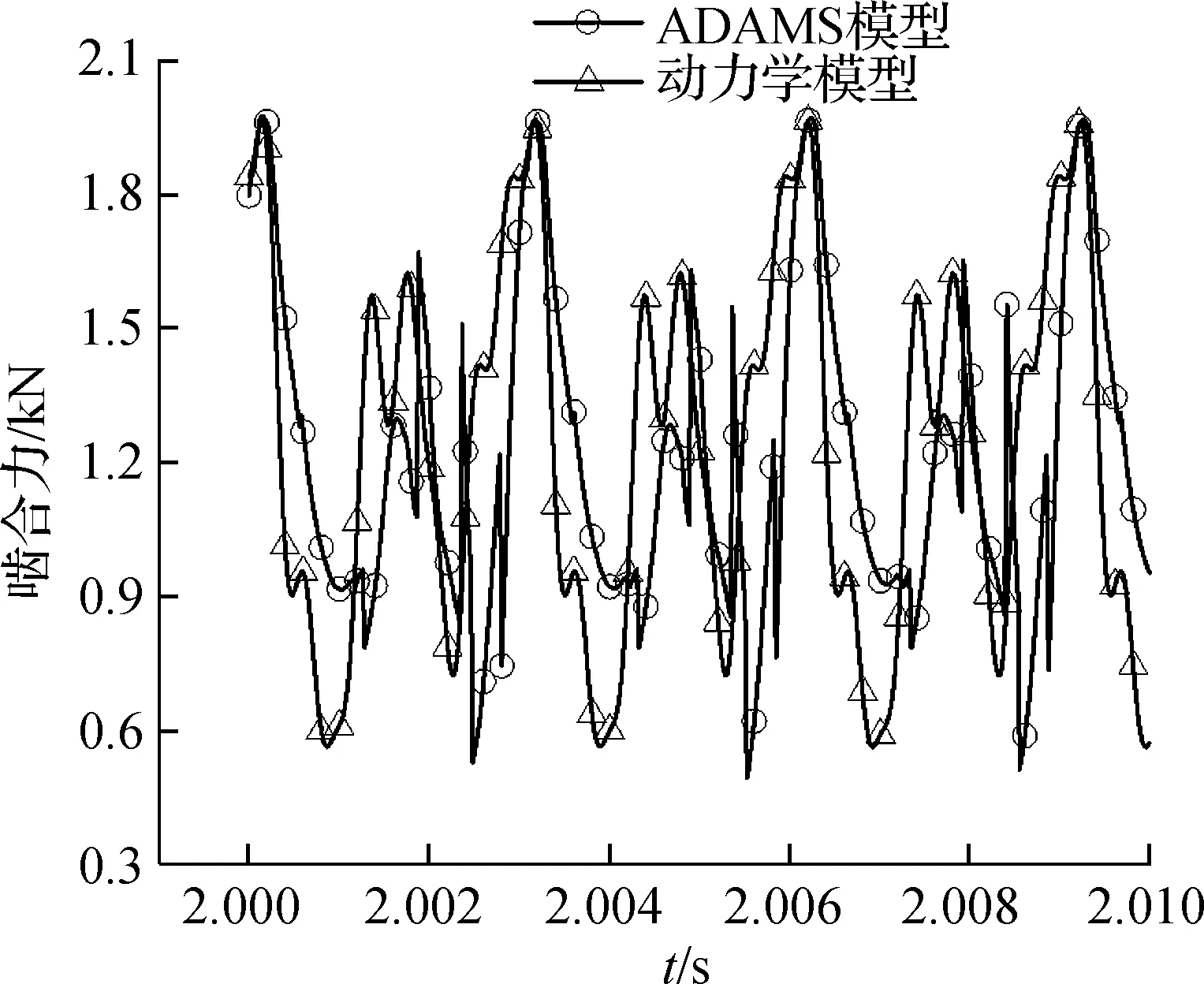
(b) 齿对34
2.2 角速度
理想状态下齿轮角速度应为恒定值,但由于振动的存在导致角速度出现波动,波动越大,振动越强烈.如图5所示,胶印机滚筒齿轮的角速度也具有周期性质,ADAMS模型的波动幅度同样大于动力学模型.图5(a)中,ADAMS模型的波动幅值约为13°/s,动力学模型的波动幅值则约为10°/s.图5(b)中,ADAMS模型和动力学模型的角速度基本是围绕1 700°/s(理想转速)上下波动,分析结果说明了稳态工况下齿轮角速度是理想转速与振动的叠加.
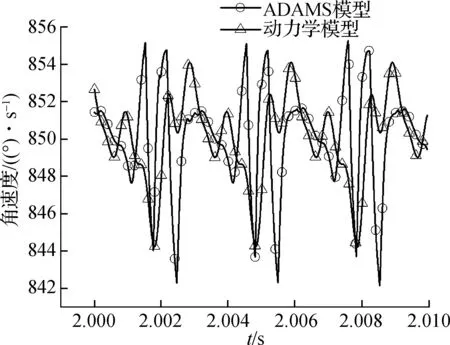
(a) 传纸滚筒斜齿轮

(b) 印版滚筒斜齿轮
2.3 加速度
加速度有效值能反映某一时间段振动能量的大小,是衡量振动强度的重要指标.图6给出了压印滚筒斜齿轮和印版滚筒斜齿轮在工作转速范围内(4 000~17 000 r/h)的X,Y,Z和三向合成加速度有效值.总体而言,加速度随转速的提高而增大,在7 000, 11 000, 16 000 r/h转速下出现峰值,表现出加速度共振峰特征.Z方向的加速度小于X,Y方向,原因可归结为轴向力波动相对较小.
2.4 啮合刚度
大量研究证实,啮合刚度激励是引起齿轮系统振动的主要原因之一,齿轮啮合过程中,刚度波动越大振动越强烈,啮合刚度的平稳性对齿轮减振有重要意义.标准差是衡量啮合刚度周期波动大小的一个有效指标,能反映齿轮动态设计的优劣.如图7所示,螺旋角和压力角的变化对啮合刚度波动(齿对12)有显著影响.
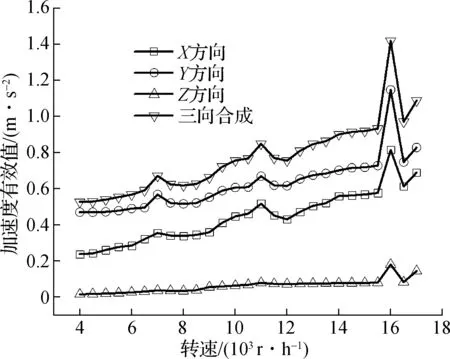
(a) 压印滚筒斜齿轮
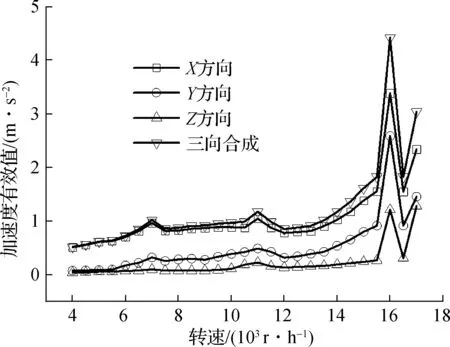
(b) 印版滚筒斜齿轮
图7(a)中压力角恒定为20°,当螺旋角为10°和20°时,啮合刚度标准差较小;螺旋角为16°时标准差较大;当螺旋角小于10°时,标准差随螺旋角的减小而增大;当螺旋角大于22°时,标准差随螺旋角的增大而增大.这说明需要合理设计胶印机滚筒斜齿轮的螺旋角以降低振动强度.
图7(b)中螺旋角恒定为15°,当压力角为16°时,啮合刚度标准差最小,压力角偏离16°越大,标准差越大,振动越强烈.
3 结论
1) 基于集中参数法建立胶印机多级平行轴滚筒齿轮动力学模型,利用Newmark-β法求解系统控制方程,分析了齿轮系统的动态啮合力、角速度、角加速度以及啮合刚度标准差,通过与多体动力学ADAMS仿真软件的对比,验证了动力学模型的计算精度.
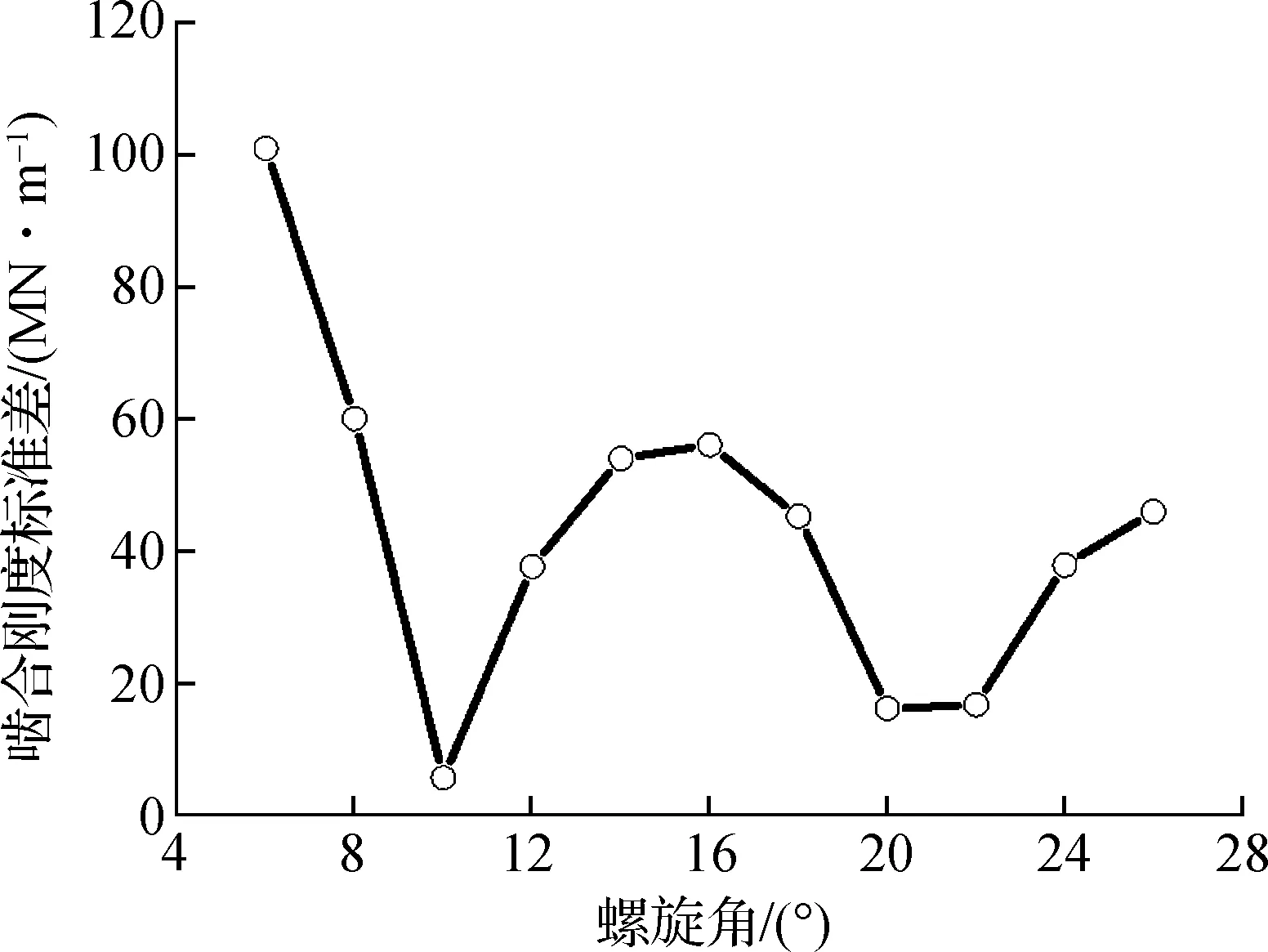
(a) 螺旋角

(b) 压力角
2) 斜齿轮的啮合力具有周期性质,呈上下波动状态,波动越剧烈,动载系数越大,振动越强烈.
3) 总体上,加速度随转速的提高而增大,在印刷速度范围内存在几个共振峰,尤其以16 000 r/h最明显.
4) 螺旋角为10°、压力角为16°时啮合刚度标准差较小,齿轮系统具有较好的动态特性.

