钢框架结构抗连续性倒塌性能试验研究

张 雷 李泓昊

(哈尔滨工业大学结构工程灾变与控制教育部重点实验室， 哈尔滨 150090)(哈尔滨工业大学土木工程智能防灾减灾工业和信息化部重点实验室， 哈尔滨 150090)

建筑结构的连续性倒塌是一个高度非线性的复杂动力过程，因此很难利用简单的结构分析方法准确地对该问题进行研究.试验与数值模拟是研究连续性倒塌问题的两大方法.连续性倒塌试验高成本、高难度、高风险的特点以及计算机仿真技术的高速发展共同促使数值模拟成为研究建筑结构连续性倒塌的主要手段.然而，为了提高计算模型的准确性以及可靠性，需要更多的高质量试验数据对计算模型进行验证.

钢结构连续性倒塌试验可分为三大类：①平面双跨梁柱子结构试验；②整体结构体系试验；③单层子结构试验.大部分连续性倒塌试验研究可归为第1类，该类试验着重考察梁柱节点在中柱失效工况下的抗倒塌性能[1-6].通过密集地布置各类测量仪器，能够较为精细地研究结构的倒塌机理.然而，该类试验仅能考虑梁柱节点在平面内的反应，忽略了对结构的抗倒塌性能具有重要影响的三维效应.第2类试验对完整建筑物在某(些)柱失效情况下的反应进行测试，从而评估该结构体系的鲁棒性.然而，由于需要利用即将拆除的建筑进行试验，而适合进行倒塌试验的待拆建筑较难寻找，试验难度大，成本高昂，具有一定的危险性，且难以布置测量仪器，因此该类试验比较稀少[7-8].考虑到前2类连续性倒塌试验的优缺点，第3类试验方案相对比较合理[9-10].这是由于：①它可以通过合理的仪器布置获得充足的数据，从而对各种抗倒塌力学机制进行辨别和分析；②试验所用试件为三维，可以考虑三维效应对结构鲁棒性的影响；③试件尺寸不会过大，试验可以在一般的结构试验室中进行.然而，现有的单层子结构连续性倒塌试验并没有系统地定量阐明钢框架结构连续性倒塌机理.

为了解决上述问题，本文进行了一单层2跨×2跨的钢框架结构连续性倒塌试验，考察了该结构在中柱失效工况下的抗连续性倒塌性能，定量地阐明了随着结构变形的增大，弯曲效应以及悬链线效应的发展及其对结构抗倒塌能力的贡献，并简要分析了梁柱节点形式对结构抗倒塌性能的影响.

1 试验概况

1.1 试件设计

本文所采用的原型结构为按照《钢结构设计规范》(GB 50017—2003)[11]设计的6层钢框架结构，从原型结构中取一个2跨×2跨的部分，按照1∶3的缩尺比设计并制作试件(见图1).试件2个方向的跨度均为2 m，层高为1 m，并未考虑楼板作用.试件中的主梁、次梁以及柱均为H型钢，所用钢材为Q345，所有的梁柱节点均为全焊接刚性节点，主梁与次梁则采用螺栓铰接的形式.中柱为一400 mm长的无支撑短柱，以模拟中柱失效的工况，其余各柱的柱脚则用地锚固定在实验室刚性地板上.如图1(b)所示，在试件第2层的中心位置留有一400 mm×400 mm的方框，加载装置可以通过方框安装到中心短柱上.方框四边通过3根平行放置的H型钢与周边结构构件相连，以确保在加载过程中方框不产生过大的竖向位移.各柱的柱顶亦通过钢梁相连.这种结构布置可以有效地限制柱顶变形，以此模拟上部结构对柱顶的约束作用.因此，尽管该试件有2层，但是2层结构构件的作用仅仅是提供必要的边界条件，因此本试验仍属于第3类试验，即单层子结构连续性倒塌试验.主要结构构件尺寸见表1.

(a) 一层平面

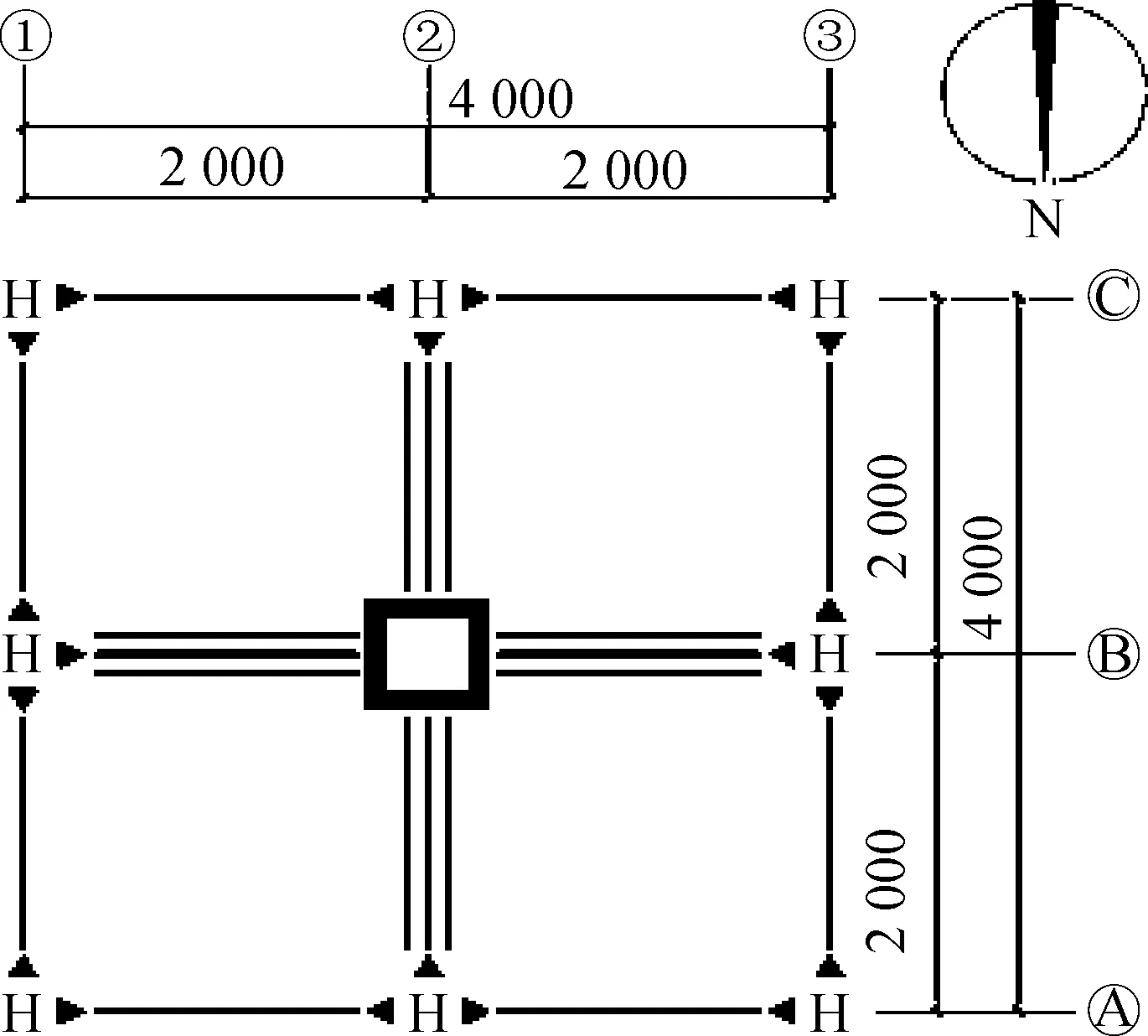
(b) 二层平面

1.2 加载与测量

采用备用荷载路径法进行准静态push-down试验，利用大行程液压千斤顶对中柱柱顶施加竖向集中荷载.试验采用分级加载方式，在利用有限元计算模型估算的模型反应的弹性范围内采用荷载控制，之后采用位移控制.试验装置如图2所示.在梁B-B12以及梁B-B23的跨中布置约束装置以防止其侧向变形.考虑到次梁对主梁侧向变形的约束作用，梁B-AB2和梁B-BC2并没有设置类似限位装置.对加载装置施加滑动约束，以保证整个试验过程中所施加的荷载保持竖直.考虑到安全问题，一旦钢梁钢材发生断裂破坏，试验终止.

表1 结构构件尺寸

观测项目包括中柱竖向荷载以及竖向位移、主梁竖向变形、梁柱节点处的水平位移以及主梁关键截面(1/3跨和2/3跨截面)的应变.

图2 试验装置

2 试验现象与破坏模式

试验结束后，试件的破坏模式如图3所示.加载初期，试件处于弹性工作阶段，无明显试验现象；中柱位移达到40 mm时，中柱附近梁B-AB2以及B-BC2的上翼缘发生局部屈曲；中柱竖向位移达到200 mm后，连接主次梁的螺栓逐渐发生剪切破坏；位移达到300 mm时，主梁发生弯扭屈曲；最终，当中柱的竖向位移达到420 mm时，中柱附近梁B-B12的下翼缘发生撕裂，试验停止.试验后期，由于主梁中产生的悬链线效应，试件周边梁柱节点发生明显的朝向中柱方向的侧向位移.

图3 试件最终变形形态

3 试验结果与分析

3.1 荷载-位移关系

图4给出了中柱的竖向荷载与竖向位移的关系.由图可见，试验初期，荷载随位移线性增长，结构反应处于弹性阶段，当竖向荷载达到120 kN，所对应的竖向位移为24 mm时，弹性阶段结束，结构在弹性段的刚度约为5 000 kN/m.当竖向位移在24～40 mm之间时，曲线处于弹塑性阶段，此时结构反应开始呈现非线性并且结构刚度开始下降.竖向位移超过40 mm后，弹塑性阶段结束，结构反应进入塑性范围，然而此时中柱竖向位移和荷载的关系十分接近线性.因此，本试验得到的荷载-位移曲线可以用弹性阶段刚度为5 000 kN/m，塑性阶段刚度为620 kN/m(约为弹性阶段刚度的12%)的双线性模型近似.当竖向位移达到421 mm时，竖向荷载达到最大值385 kN，梁B-B12下翼缘钢材随即发生断裂，出于安全考虑，试验终止.

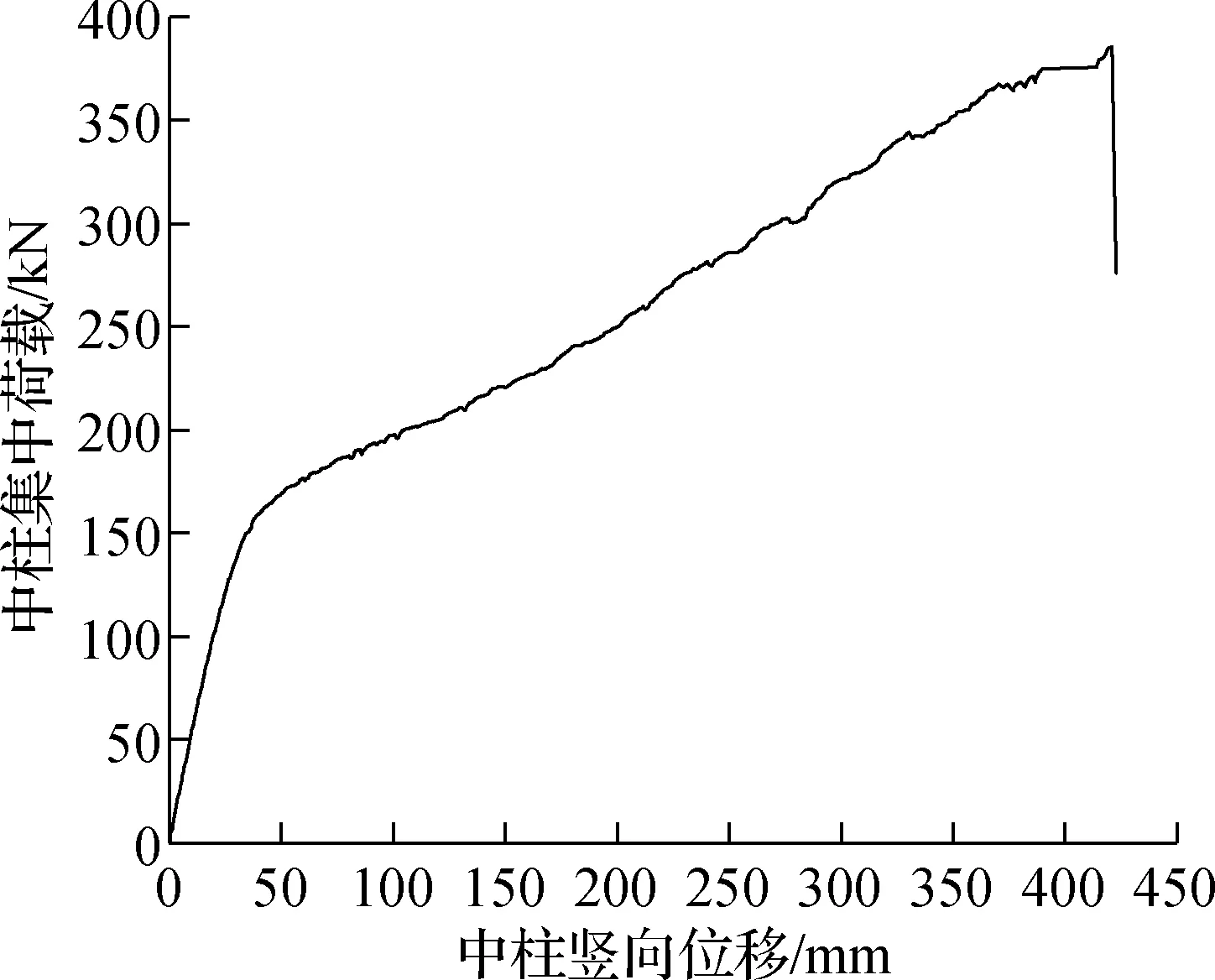
图4 荷载-位移曲线

由试验结果可知，施加在中柱的最大竖向荷载约为荷载设计值的5倍左右，由此可以确定，该结构体系并没有发生连续性倒塌的风险.

3.2 梁柱节点水平位移

梁柱节点处的水平位移如图5所示，图中负值表示节点产生向内即朝向中柱的水平位移.MC-X-N为梁柱节点的编号，其中MC表示刚性节点，X表示节点所连接的主梁，N表示节点所处梁端的方位.由图5可看出，在加载初期即弹性和弹塑性阶段，节点MC-B12-E和MC-B23-W产生远离中柱的水平位移，当中柱竖向位移超过60 mm后，才逐渐向内移动.而节点MC-AB2-N和MC-BC2-S则一直朝向中柱移动.当中柱竖向位移小于100 mm时，各梁柱节点的侧向位移并不明显(小于4 mm)，且增长缓慢.但中柱竖向位移超过100 mm后，各节点朝向中柱方向的侧向位移迅速增大，说明梁中的悬链线效应开始发展.在试验结束之前，各节点向内的侧向位移均达到50 mm左右.这一现象证明结构体系抵抗连续性倒塌的力学机制由弯曲机制逐渐向悬链线机制转变.

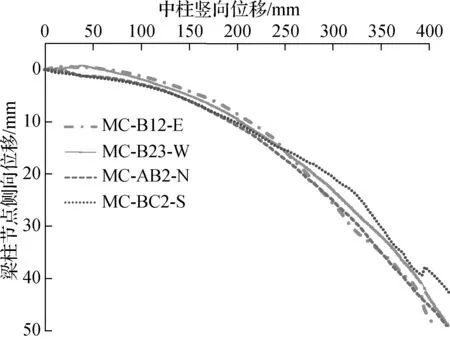
图5 梁柱节点的水平位移

4 抗倒塌力学机制分析

对于钢框架结构，在中柱失效后，通常有2种力学机制能够提供竖向抗力以抵抗连续性倒塌的发生：①受弯机制，即小变形情况下通过梁的抗弯效应来抵抗倒塌；②悬链线机制，即大变形情况下由于梁端塑性铰的形成，梁中产生大量轴力，能够为结构体系提供抗力.如果能够通过试验测得的数据对主梁的内力即弯矩和轴力进行分离和计算，就可对这2种抗倒塌力学机制的形成和发展进行定量分析.整个加载过程中，布置在各主梁1/3跨以及2/3跨处截面的应变片读数均在2.0×10-3以内，说明这2个截面的材料在试验过程中始终保持弹性状态.同时，这2个截面不会受到试验后期在中柱节点附近发生的钢梁上翼缘的局部失稳现象的影响，结构的破坏并不会影响应变片的测量精度.因此，可利用这2个截面的应变片读数计算主梁中内力随中柱竖向位移的变化.

假设某主梁距中柱1/3跨处截面S-X-2的内力为VX-2,NX-2,MX-2, 距中柱2/3跨处截面S-X-3的内力为VX-3,NX-3,MX-3(见图6),其中下标X代表主梁编号.主梁X的弯矩MX-2，MX-3以及轴力NX-2，NX-3可根据应变片读数直接求得，剪力VX-2以及VX-3可由梁中弯矩计算而得(见图6(b))，即

(1)

利用S-X-2截面的剪力和轴力(见图6)，可计算某一主梁对结构体系竖向抗力的贡献为

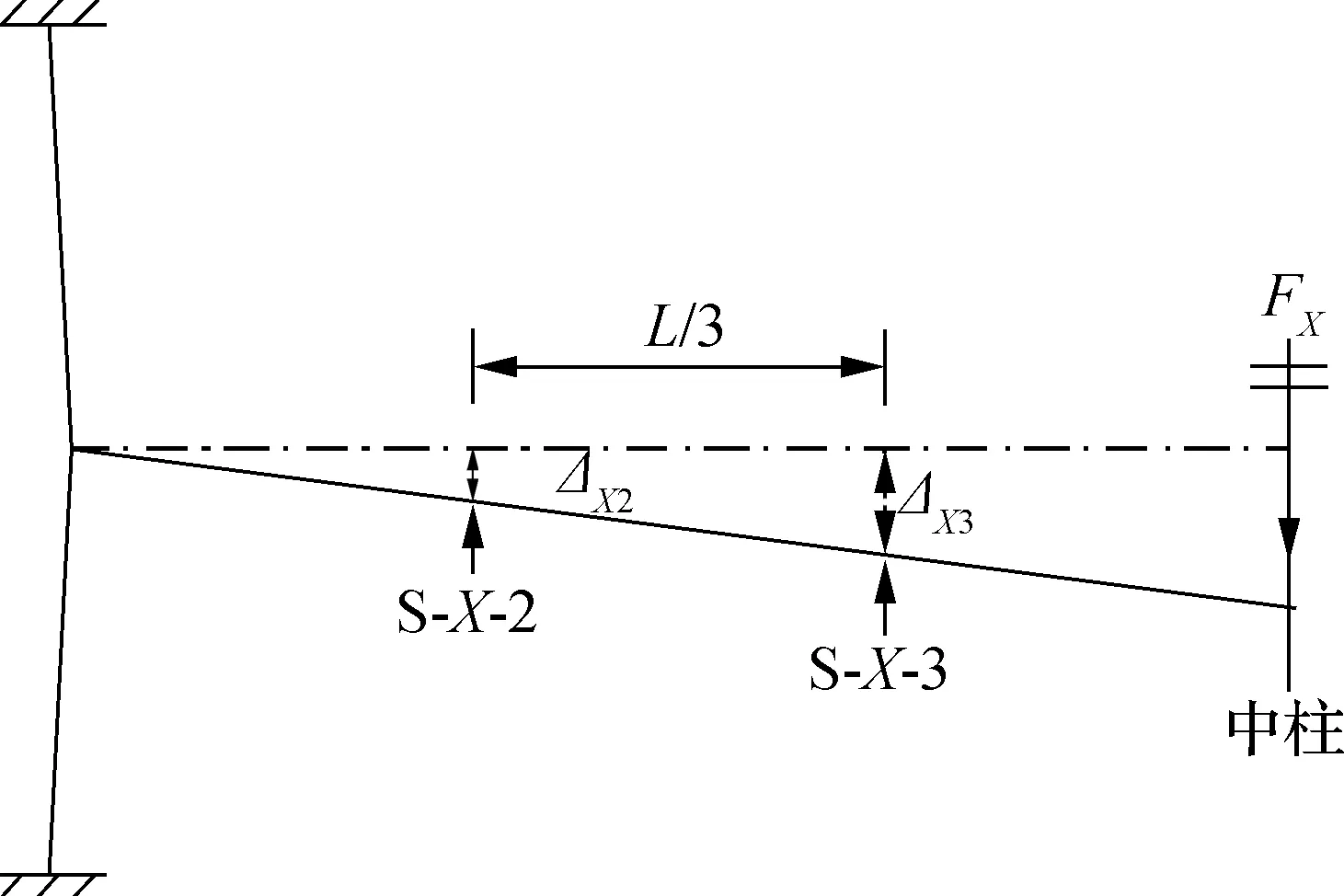
(a) 计算模型

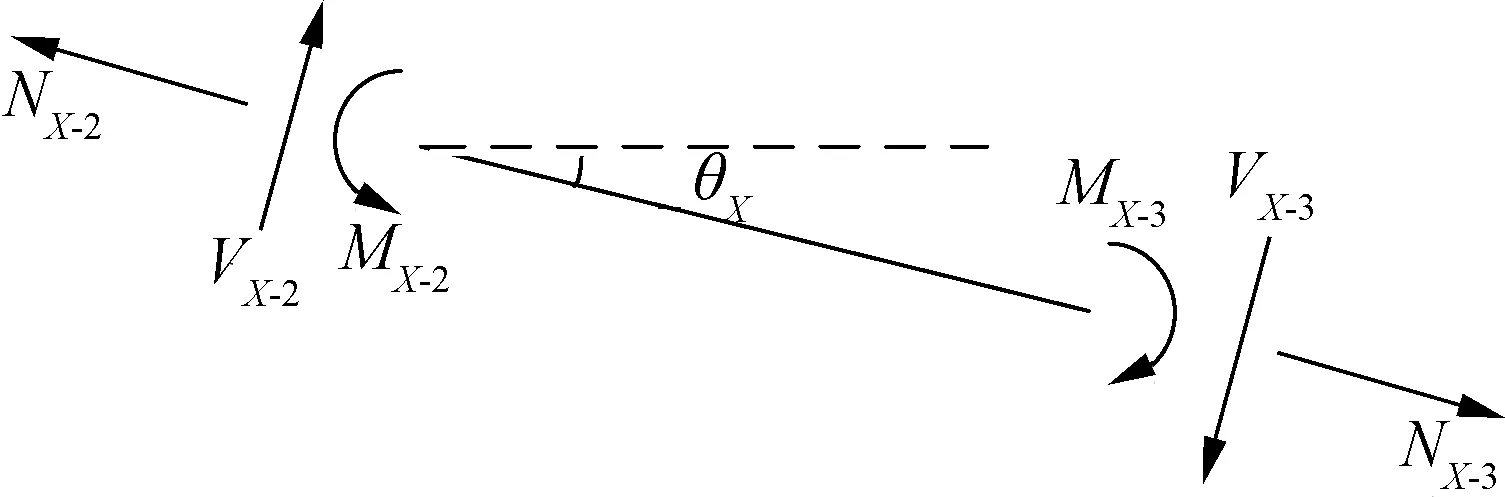
(b) 主梁截面内力

FX=VX-2cosθX+NX-2sinθX

(2)

式中，θX为截面S-X-2的转角，考虑到加载过程中S-X-2与S-X-3之间的梁段变形基本呈直线，故θX可根据S-X-2和S-X-3处的竖向位移确定，即

(3)

式(2)中，截面剪力以及轴力在竖直方向上的分量VX-2cosθX以及NX-2sinθX分别代表弯曲效应以及悬链线对结构体系抗倒塌能力的贡献.

中柱柱顶处所施加的竖向荷载为各主梁对结构竖向抗力贡献值之和，即

F=∑FX=∑(VX-2cosθX+NX-2sinθX)

(4)

图7对比了弯曲效应和悬链线效应对结构竖向抗力的贡献随中柱竖向位移的变化.结果显示，当中柱竖向位移小于40 mm时，结构的竖向抗力仅由弯曲效应提供，主梁中并没有轴力产生.当中柱竖向位移增长到120 mm时，梁中有少量轴力产生，由于悬链线效应产生的抗力仅占结构体系总抗力的5%左右；当竖向位移达到240 mm时，这一比例增长至17%；此后，随着中柱竖向位移的进一步增长，弯曲效应对结构竖向抗力的贡献开始缓慢下降，而悬链线效应产生的竖向抗力则迅速增加；当中柱竖向位移增长至370 mm时，悬链线效应产生的竖向抗力超过弯曲效应产生的竖向抗力，悬链线效应成为结构抗连续性倒塌的主要力学机制；试验临近结束时，悬链线效应和弯曲效应提供的竖向抗力占结构总抗力的比例分别为60%和40%.总之，在小变形情况下，弯曲效应是抵抗连续性倒塌的主要力学机制，此时悬链线效应对结构抗倒塌能力的贡献十分有限；然而，随着中柱竖向位移的增长，悬链线效应逐渐发展，对结构抗倒塌能力的贡献越来越大；在大变形情况下，弯曲效应对结构抗倒塌能力的贡献虽然仍旧不可忽略，但悬链线效应对结构的最终抗倒塌能力有着更为重要的影响.

这一现象与采用螺栓连接的半刚性与柔性节点的钢结构抗连续性倒塌性能试验结果[2-3]有明显区别.这些试验中，在加载的最后阶段，弯曲效应由于部分螺栓的破坏而消失，结构抗力仅由悬链线效应提供.因此，节点形式对结构的抗倒塌力学机制的发展起到决定性作用.

5 结论

1) 试件在中柱失效情况下表现出良好的鲁棒性.试件可以承受的施加在中柱顶部的竖向集中荷载最大值达到385 kN，为中柱所承担荷载设计值的5倍左右，中柱最大竖向位移可达421 mm.由此可以推断，在中柱突然失效的情况下，该钢框架结构并不会发生连续性倒塌.

2) 在加载初期，弯曲效应为结构抵抗连续性倒塌的主要力学机制.在中柱竖向位移达到240 mm之前，弯曲效应提供的竖向抗力占结构总抗力的80%以上，此时主梁中虽然有轴力产生，但是悬链线效应对结构抗连续性倒塌能力的贡献十分有限.

3) 大变形情况下，由于弯曲效应产生的竖向抗力逐渐减小，而悬链线效应则迅速发展，在中柱竖向位移达到370 mm时，悬链线效应对结构竖向抗力的贡献超越弯曲效应，成为主要的抗连续性倒塌力学机制，最终悬链线效应产生的竖向抗力占总抗力的比例达到60%.在试验后期，虽然弯曲效应对结构抗连续性倒塌性能的贡献有所减少，但依然显著.

4) 节点形式对结构的抗倒塌力学机制的发展起到决定性作用.