板材弯曲工艺中基于模型的回弹研究

高强度钢板对减轻车重起着关键作用，在汽车零部件中得到了越来越多的应用，从而使汽车零部件的轻量化和耐撞性都得到了提高，同时钛合金在轻量化结构中也越来越受到关注。汽车及其相关行业的产品竞争非常激烈，零件制造商非常希望缩短模具设计和试模周期，因此需要更精确的分析方法来改善成形部件的质量并减少制造缺陷。

高强度钢板和钛合金板在成形时，主要挑战之一是卸载时的回弹，其中钛板相对于先进高强钢板的回弹量更大。这将致使所成形出零件的尺寸精度低，对零件最终几何形状有很大影响，并且可能影响装配。这是汽车工业中亟待改善的一个关键问题。

在钣金零件的加工和模具设计过程中，广泛应用有限元模拟预测回弹。而有限元模拟的精度依赖于所使用的材料模型。本文将介绍在多种弯曲情况下，结合试验，通过改进材料的本构模型、硬化模型、弹性模型、边界条件来提高有限元回弹仿真精度，提高对回弹的预测能力；研究材料的微观结构、模具参数、温度对回弹的影响。同时介绍了一种回弹在线测量方法。

1 应用新的本构模型分析钛合金在弯曲和辊压成形中的回弹行为

作者此文之前的研究是完善与应变路径相关的本构模型来描述钛合金在室温下的非弹性行为，本文对其进一步扩展。通过将纯弯曲和拉伸-压缩试验与反分析结合，确定了钛合金的基于各向异性硬化模型的均匀屈服函数模型（HAH）的循环硬化特性，并用该模型描述了非比例应变路径变形过程中各向异性屈服面的演化;优化本构模型（见图1）参数，将获得的钛合金在纯弯曲和拉伸-压缩中的循环特性整合至V模弯曲和滚压成形工艺的数值模型中以分析回弹。

该模型与试验结果吻合度高，再现了辊压成形的低回弹。各向同性材料模型与V模弯曲试验具有良好的回弹相关性，但却高估了辊压成形工艺的回弹，这表明在辊压成形中观察到的低回弹可能由运动硬化效应引起。因此，为了精确预测辊压成形的回弹，需要考虑运动硬化效应。

对由V模弯曲和辊压成形生产的对称V形截面进行数值分析，将模拟结果与使用各向同性硬化模型和先前的试验测量结果进行比较，得到如下结论[1]：

（1）通过在室温下基于钛合金板材HAH模型的本构描述，能精确地得到材料在加载和加载路径反转阶段的硬化特性。

（2）该模型精确地预测了V模弯曲工艺和辊合金压成形中钛合金的回弹行为，并且相比于之前的弯曲试验能够捕获较低的回弹。

（3）虽然回弹的测量值与仿真值能够较好的吻合，但若将弹性模量随有效成形应变的变化考虑在内，可以进一步提高材料模型的精度。

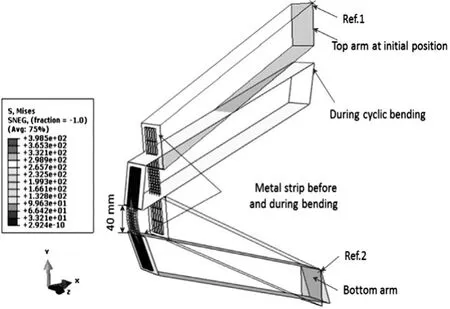
图1 循环纯弯曲试验的有限元模型【1】

2 先进高强钢板双级U形拉弯回弹预测的先进本构模型

为减少AHSS板材的回弹量，提出了采用两步拉深成形工艺(双级U形拉弯)生产U形槽的方法。使用有限元分析模拟该过程，其中应用两种各向异性硬化模型，即各向同性-运动模型和扭曲模型，来描述在应变路径变化期间的包辛格效应和相关的各向异性硬化瞬变。此外，还考虑了不同屈服函数捕获的塑性各向异性和弹性模量的退化。除了进行基本的力学表征试验以确定材料系数外，还进行了平面内压缩-拉伸实验。对双级U型拉伸弯曲过程的实验（图2）和有限元模拟结果进行了对比分析，以了解非比例加载下各向异性硬化对回弹的影响。结论如下[2]：

（1）对DP 980和TWIP 980板材进行了单级和双级U形拉伸弯曲试验。其中双阶段U形拉弯的回弹量较低，从而减小了整个试件的弯矩。在单级U形拉伸弯曲中，回弹量最大的材料，在双阶段U形拉弯后，回弹下降幅度最大。

（2）用四组不同的本构模型进行了有限元模拟。在单级U形拉伸弯曲过程中，各向同性硬化模型高估了回弹，且在双级弯曲后，误差明显增大。但先进的本构模型使得对回弹的预测与单级和双阶段U形拉伸弯曲的实验结果吻合较好。然而随着成形和卸载阶段的增加，有限元预测误差预计会增加。

（3）YU和HAH模型对TWIP 980板材的回弹预测结果类似。对于DP 980，这两种模型的预测值相差很大，因为这两种模型所识别的材料系数都在2%以下，虽然在较小的应变范围内用这些模型得到了相似的流动曲线，但是对于较大的应变，情况并非如此。因此，材料系数应在足够宽的应变范围内确定，以准确预测双阶段或多阶段成形过程中的回弹。

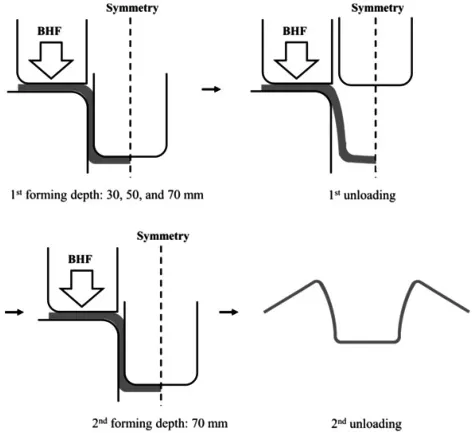
图2 双级U形拉伸弯曲试验布置

3 U形高强度钢回弹测量中变弹性模量与非线性运动硬化耦合的研究

由于先进高强钢具有合适的比强度，在汽车工业中得到了广泛的应用。该合金具有独特的硬化性能和可变的卸载弹性模量，本文介绍了一种预测正常和预应变DP 780双相钢带U形弯曲回弹的解析模型，它基于Hill48屈服准则和平面应变条件。该模型考虑了成形历史、板料变薄和中性面运动对回弹的影响，采用各向异性非线性运动硬化模型(ANK)来考虑拉伸、弯曲和反向弯曲等复杂变形的影响。该模型能够研究包辛格效应、瞬态行为和永久软化，利用塑性应变的非线性函数来捕捉可变卸载弹性模量。该模型用于解决Numisheet 2011基准U形弯曲问题，研究了夹持力、摩擦系数、厚度、材料各向异性、硬化参数、预应变和变弹性模量对板料回弹的影响。结果表明[3]：

1）考虑变弹性模量的回弹角预测量略大于恒定弹性模量。与解析模型相比，变杨氏模量的有限元解与实验结果吻合较好，这是由于解析解的简化所致。

2）随着硬化参数γ1和C2的增加，回弹角增大，侧壁曲率半径减小；而随着C1的增加，回弹角减小，侧壁曲率半径增大。另外，减小饱和杨氏模量会导致回弹角的增大和曲率半径的减小。上述这些变化更适用于预应变情况。

3）压边力和模具与板料之间摩擦力的增加导致回弹下降。冲头摩擦只影响区域II中的回弹角，随着冲头摩擦的增加，回弹角增大。

4）回弹随毛坯初始厚度的增加而减小，而随板料各向异性的增加而增大。此外，预应变导致回弹参数的变化减小。这一模型可被视为基准模型，以考虑相对复杂的硬化模型的相似本构方程的效率、最终的数值误差的独立性。

4 考虑应力反转后的非线性弹塑性以提高回弹预测精度

由于近来在汽车白车身部件中应用高强度钢的趋势，预测冲压成形工艺的回弹变得更加重要。回弹预测的精度取决于对卸载后回复应变的估计。众所周知，预应变后的卸载特性为非线性的应力-应变关系，因此非线性弹塑性材料模型对于精确的预测回弹是必要的。在材料试验中（图3），在卸载和再加载阶段的单轴、双轴应力状态下测量高强钢板的应力-应变特性，将非线性材料模型应用到有限元软件LSDYNA中。对帽形构件进行冲压成形试验和相应的回弹分析，并评估回弹角来探究回弹预测精度。得到如下结论[4]：

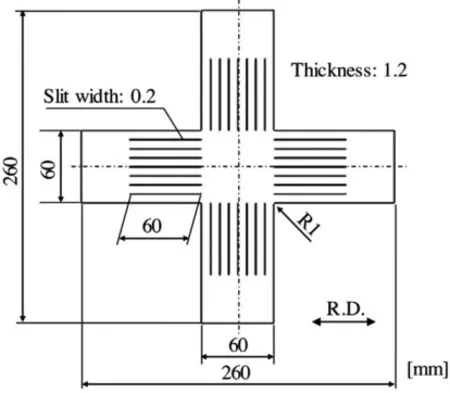
图3 用于双轴拉伸试验的试样几何形状[4]

1）当梯度由新定义的参数决定时，在不同程度预应变后的卸载和再加载阶段的应力-应变梯度彼此一致。在单轴和双轴应力状态下均观察到该试验趋势。应力反转后的非线性行为由应力改变量决定。

2）材料模型的特征：该模型有两个面，屈服面应用运动硬化，边界面应用各向异性硬化；屈服面的尺寸设置的足够小，以描述应力反转后的非线性行为；回复应力和系数C的方程定义为屈服面与应力反转距离的函数。

3）该模型可以描述应力反转后的非线性行为。

4）该模型的回弹预测结果与试验结果有较好的一致性。这是因为考虑了卸载时的包辛格效应和非线性，该模型精确地估计了冲头下止点的应力和回弹的回复应变。

5 改进回弹模拟的双相钢滞弹性模型

经典的弹塑性模型假设屈服面内的所有应力满足线弹性应力-应变关系。最近的研究表明在弹性域内存在着取决于先前塑性变形的非线性关系。“卸载应变”分为线弹性部分和与晶格中的可逆位错运动有关的滞弹性部分。卸载时恢复应变中的滞弹性贡献是显著的，因此在回弹预测时应考虑滞弹性，此现象的E模量衰退模型是错误的，只有在材料完全卸载后才能给出合理的应变预测。回弹时板料的内部纤维部分卸载，外侧纤维甚至在压缩中再加载，因此需要一个包含塑性预加载量和卸载量的模型。为了在有限元程序中实现该模型，需要在完整的六维应力空间中而不仅仅是单轴应力下规划。

在此研究中，基于该现象的物理特性量化滞弹性应变，提出了描述非线性卸载行为的一维模型[5]，其被推广到包含弹性、非弹性和塑性应变的三维本构模型。通过比较所预测的循环卸载/再加载应力-应变曲线与试验曲线评估模型的性能。

在该研究中建立了捕获先进高强钢非线性卸载/再加载行为的模型[5]，并使用在循环卸载/再加载实验中获得的DP800钢的实验数据校准该模型。为此，将四个参数拟合到实验数据中。实验结果与模型之间的比较显示了整个卸载/再加载路径的良好相关性。因此，使用该模型模拟成形工艺，能够更好地预测复杂构件的回弹。

6 边界条件对板料成形回弹及起皱预测的影响

目前在汽车工业中使用的高强度钢板在成形过程中容易出现非传统行为，同时也是数值模拟中最具挑战性的两种几何预测：起皱和回弹，因此有限元法需要精确可靠的数值模型。本文对一种具有高起皱倾向和2D回弹的钢轨部件进行了试验和数值分析。板坯使用两种不同的材料，即低碳钢（DC06）和双相钢（DP600）。通过平板试验评估每一金属板材与成形工具之间的摩擦行为，从而确定摩擦系数作为常压的函数。用两种不同的数值模型(全尺寸毛坯模型和对称条件下的1/4毛坯模型)评价了应用边界条件对数值结果的影响。实际上，全尺寸毛坯模型的数值结果与实验结果吻合较好，但考虑全尺寸毛坯的数值模拟的计算成本大大高于使用1/4的毛坯。

本文中，第二节描述了成形过程的实验设置，包括用于评估作为正常接触压力函数的摩擦系数的程序；第三节给出了所提出的有限元模型，考虑了毛坯的不同边界条件和毛坯与刀具接触行为的摩擦模型；第四节对实验结果和数值结果进行了比较，着重介绍了毛坯材料和所采用的有限元模型的影响；第五节概述了本研究的主要结论。结果表明[6]：

1）回弹的大小受坯料强度的影响很大。实际上，双相钢中的法兰回弹角比低碳钢高约3倍。两种材料的数值计算结果与实验结果吻合较好，但数值模拟略微高估了冲压力的演化，特别是在低碳钢中。

2)毛坯材料以及数值模型中定义的对称条件对起皱行为有很强的影响。由于所选材料的机械强度相差很大，钢轨顶面起皱的形状取决于材料。虽然两种有限元模型对回弹力和成形力的计算结果是一致的，但皱纹的形状取决于所采用的数值模型。

7 基于微观结构的AHS钢回弹效应研究

在汽车零件的板材成形过程中，回弹效应至关重要，特别是对于先进高强钢（AHS），不同相之间的局部相互作用对宏观响应起着重要作用，大多数形状复杂的结构部件需要多次成形。因此，需要更好地理解和更精确地描述这种钢板成形中的塑性变形行为和回弹。

本文的目的是在宏观和微观层面研究780AHS钢板和1000AHS钢板的回弹效应。首先，进行不同预应变的循环拉伸-压缩试验，从循环应力-应变响应中确定Y-U模型的材料参数。对微观结构进行了RVE模拟，并对其有效的单调流动应力曲线进行了预测。然后，结合文献数据进行回归分析，确定了单相钢的Y-U参数，将其与运动硬化模型耦合，在拉伸-压缩载荷下进行RVE模拟，并用实验曲线对算得的宏观循环应力应变曲线进行验证。随后，对改进的帽形试样进行成形试验，并进行相应的有限元模拟，对试件回弹角和侧壁卷曲的试验和预测值进行了比较。此外，利用Y-U模型对板料成形过程中模具半径附近的局部区域进行了RVE模拟，对所研究的两种钢的应力、应变分布和组织变形进行了分析和讨论。得到结论如下[7]：

1）所进行的拉伸–压缩试验可提供完全循环的应力–应变曲线，具有相同的正、负应变范围。两个钢种的应力-应变曲线适用于确定Y-U模型参数，该参数通过帽形试样的回弹预测结果得到了充分验证。

2）通过RVE模拟精确预测了钢的拉伸有效应力-应变曲线（图4）。

3）根据计算出的拉伸流动应力曲线，结合文献数据对初始屈服应力的回归分析，可以确定被试钢各相的Y-U模型参数。使用与参数确定的Y-U模型相结合的RVE模拟拉伸-压缩，得到的应力-应变响应与实验结果吻合较好。

4）采用RVE模拟，结合各向同性和运动硬化模型，研究了帽状试样在成形过程中沿凸缘边缘移动的微观组织的应力和应变特征。发现基于微观结构的Y-U模型可以更好地描述钢的包辛格效应、瞬态行为和永久软化。Y-U模型中铁素体和马氏体相的局部等效应力明显低于各向同性模型，在钢的强度较高的情况下，用硬化定律计算得到的应力应变差异较大。

5）该建模方法可以作为合并微观结构对先进高强钢板回弹预测影响的基础。

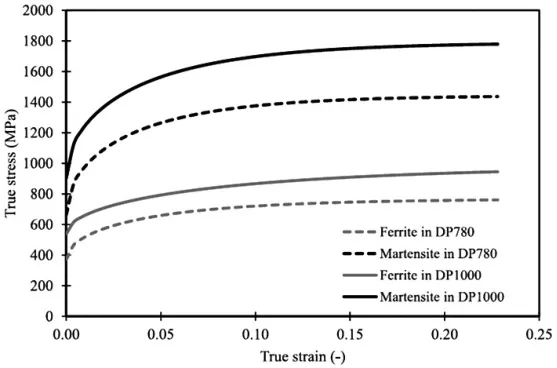
图4 单相铁素体和马氏体的流动应力模拟【7】

8 U形弯曲过程中通道宽度对回弹特性影响的有限元分析

在这项研究中，通过试验和有限元法探究了通道宽度对U形弯曲过程中回弹特性的影响。通过应力分布分析，发现当使用压力垫时，工件的弯曲应力和反向弯曲应力没有变化，通道宽度对回弹特性的影响可以忽略不计。相反，无压力垫时，通道宽度直接影响弯曲和反向弯曲应力，导致回弹特性变化。

本文得到的结论[8]：通过施加压力垫，在工件的底部表面和支腿中防止了应力的产生。工件中的弯曲应力仅沿冲头半径的接触区产生，通道宽度改变后，仍在接触区形成了相同水平的弯曲应力，以及相同的预测弯曲角度和回弹特性。在使用压力垫进行U形弯曲的情况下，通道宽度的变化对回弹特性影响不大。另一方面，在没有压力垫的U形弯曲的情况下，在底面产生弯曲应力和反向弯曲应力，并且在腿中产生反向弯曲应力。这些结果证实，通道宽度的变化极大地影响了回弹特性，应该计算回弹以达到设计要求；通道宽度小能减小回弹，通道宽度大会增大回弹。通过比较有限元模拟结果与实验结果，弯曲角度和弯曲力的误差约为1%。对于弯曲角度和弯曲力两个方面，有限元模拟结果与实验结果吻合较好（见图5）。

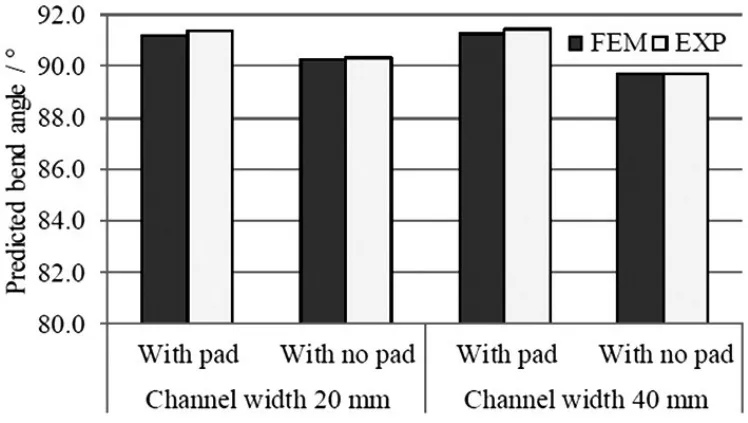
图5 有限元间弯曲角度的比较-模拟和实验结果【8】

9 纳米析出强化钢板高温弯曲回弹的粘弹塑性行为

纳米碳化物沉淀强化的高强钢板(nano-HSS)由于其在高温下组织稳定，适合于热成形。采用单轴拉伸和应力松弛试验研究了980 MPa nano-HSS从室温到973 K下的粘弹塑性行为（图6）。实验研究了板材的热V形和U形弯曲，重点研究了与温度和成形速度相关的回弹。此外，为了阐明应力松弛和卸载蠕变的影响，利用充分描述与速率相关的拉伸流动应力和应力松弛行为的粘弹塑性材料模型对热弯曲和回弹进行了数值分析。在均匀弯曲分析的基础上，重点研究了拉压过程中的应力松弛效应和卸载过程中的蠕变效应。本文的重点总结如下[9]：

图6 a）Nano-HSS和b）980MPa双相HSS在温度变形后的拉伸强度【9】

1)单轴拉伸下的流变应力随温度的升高而显著降低。在高温下（873 K以上），应力具有高的速率依赖性。快速应力松弛发生在最初几秒钟的应变保持阶段，随后松弛继续缓慢进行。目前的粘弹塑性模型充分地描述了这些材料的行为。

2)热成形回弹减少的主要原因是在高温下的低流动应力。此外，在某些情况下，应力松弛和卸载蠕变起着重要作用。

3)为了减少回弹，低速弯曲和不弯曲是最好的方法，因为它们会引起应力松弛和蠕变效应。冲头末端保持几秒钟对于减少回弹是有效的。

4)与冷成形相比，热成形的优点之一是板料的残余应力很小。

10 中空结构截面三辊推弯过程的回弹测量

三辊推弯工艺主要用于制造中空的弯曲构件。用此工艺生产新批次的产品时，需要反复进行试错试验来抵消回弹对最终几何精度的影响。通常的几种基于试验和数值的离线优化技术可以满足要求，但这需要高成本的材料标定和很长的计算周期。

本文提出一种新型的基于惯性测量技术的在线方法，并对其进行了试验验证和精度评估[10]。

管件弯曲后的实际弯曲半径，可以由已经通过成型辊的管件部分的几何轴线坐标分析计算得到；其标称弯曲半径，可以由管件分别与弯曲辊、成型辊的接触点坐标计算得到，由这两个半径来评估回弹。为了监测回弹后的轮廓曲率来得到轴线坐标，设计了一种新型芯轴。在其最后一个球头（总是与实际弯曲截面有相同的方位）内嵌入一个惯性测量单元（IMU）实时监控弯曲轮廓。IMU通过内部集成电路协议连接到作为数据记录器的微控制器来存储数据、获取电量；数据记录器与CNC机床相连，记录电机的所有动作，处理数据来计算回弹（图7）。

这种方法基于3D坐标系中角速度和加速度的测量，能在卸载之前测定弯曲轮廓的纵轴。IMU能够测量的角速度范围为正负250°/s，线性加速度范围为正负2g，采样频率为300Hz。试验验证其与接触式测量机的最大测量偏差为3.79%。这足以应用到以芯轴作为内部支撑来防止成形缺陷的中空构件的自由弯曲工艺中，并为快速矫正成形偏差提供了可能。

图7 TRPB工艺的工具和运动轨迹【10】