浅谈极坐标在高中数学中的应用

◎刘殿芳 刘秀辉

极坐标在解决圆锥曲线问题上有这非常广泛的应用，特别是极径在解决线段，弦长，距离等问题上即方便又灵活。下面从几方面探讨极坐标的应用。

一、求距离之积：一条直线与两条直线相交，求两个弦长之积

例1.曲线C1的参数方程为，（α为参数），在以原点O为极点，x轴的正半轴为极轴的极坐标系中，曲线C2的极坐标方程为ρcos2θ=sinθ（1）求曲线C1的极坐标方程和曲线C2的直角坐标方程；（2）若射线 L：y=kx（x≥0）与曲线 C1，C2的交点分别为 A，B（A，B异于原点），当斜率时。求的取值范围。

解：（1）C1的极坐标方程ρ=2cosθ，C2的直角坐标方程x2=y

（2）因为 A在圆上，B在抛物线上，设其极坐标分别为 A（ρ1，θ），B（ρ2，θ）

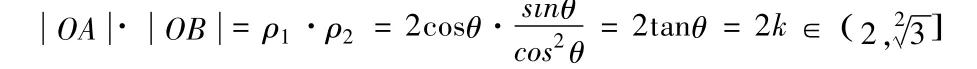
二、求距离之和：两条直线与一条曲线相交，求两个弦长之和

解：（1）得 C2：（x-1）2+y2=1，利用直角坐标和极坐标互化得：ρ=2cosθ

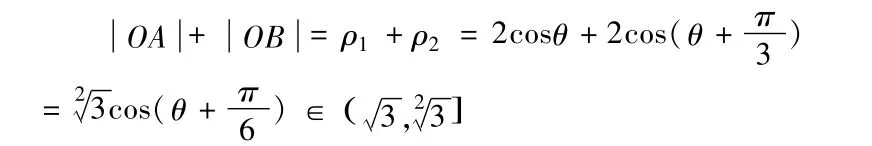
【总结】运用极坐标表示点，用极径表示线段，把距离之和转化为三角函数求最值。

三、求距离之商：一条直线与两条曲线相交，求弦长之商

例3.在直角坐标系xoy中，直线L的方程是x=2，曲线C的参数方程为（α为参数）。以O为极点，x轴的非负半轴为极轴建立极坐标系，

（1）求直线L和曲线C的极坐标方程；（2）.射线OM：θ=β（其中0）与曲线C交于O，P两点，与直线L交于点M，求的取值范围。

解（1）直线 L：pcosθ=2.曲线 C：p=2sinθ.

【总结】利用直角坐标和极坐标互化公式，将曲线方程转为极坐标方程，用极径表示线段。

四、求距离之差：一条直线与两条曲线相交，求弦长之差

（2）C3极坐标极坐标：ρ=4sinθ；

以上都很好的运用了极坐标法，解决了数学中常见的距离问题。

极坐标法是一种极其重要的解题方法，特别是本文提出的四种题型，用直角坐标解非常复杂，用极坐标法变得十分简单，便于处理。这充分体现用极坐标法解决圆锥曲线问题有着极大的优越性。通过对例题的探讨，使学生对极坐标知识有更深层次的理解和掌握。希望帮助更多学生，解决他们的困扰，准确运用极坐标解决圆锥曲线问题，提高解题能力，提升解题速度。