基于施工全过程的矩形盾构隧道结构受力分析方法及应用
梁 霄, 官林星, 温竹茵, 孙 巍, 柳 献
(1. 上海市政工程设计研究总院(集团)有限公司, 上海 200092; 2. 同济大学地下建筑与工程系, 上海 200092)
0 引言
矩形盾构隧道具有空间利用率高、采用非开挖建造工法、更好的浅覆土适应能力、对周边环境影响小、满足长距离和较小曲率半径隧道的施工等方面的优势,具有显著的经济和社会效益[1-2]。因此,在今后城市地下通道的发展中将得到越来越多的应用。衬砌结构在盾构隧道施工阶段的受力与运营阶段有较大的差异[3],面临着施工过程中各项不确定因素带来的不利影响,如何考虑施工过程中的结构受力对隧道建造和运营的安全起着至关重要的作用。
在盾构隧道结构受力研究方面,Mashimo等[4]提出在盾构管片拼装阶段,管片自重产生的地基反作用可通过弹簧支座进行考虑。官林星[5]针对盾构隧道衬砌设计的荷载-结构法,对荷载组合的方法及程序的实现进行了研究;针对地层-结构法,将施工过程分为挖土阶段、衬砌施工阶段、环间空隙被土层填满阶段、注浆阶段、注浆影响范围内土体力学性质改变阶段,并对不同施工阶段下土层的应力释放系数进行了探讨。朱合华[6]针对盾构隧道柔性衬砌设计分析方法中的荷载-结构法,提出了盾构隧道衬砌受力包络图,强调施工过程中盾构衬砌受力的变化;针对地层-结构法,主要采用有限元数值模拟方法来反映复杂施工参数的变化。刘益平[7]针对越江盾构隧道,将施工过程分为挖土阶段、盾尾注浆阶段、盾尾脱开阶段、固结沉降阶段和河床冲刷阶段等5个阶段,在确定初始应力计算、开挖释放应力计算、地层及结构材料模拟的基础上进行施工阶段的动态有限元模拟。
综上可知,已有研究主要基于施工过程的阶段划分进而采用有限元分析方法进行盾构隧道施工过程的动态模拟,主要考虑施工过程对地层应力释放系数的影响,分析结果可对结构受力进行定性分析和校核,但完全以该方法的分析结果进行结构设计尚为不妥;另外,基于荷载-结构法考虑荷载组合取包络的方法,其中的施工工况未对结构在施工期的荷载模型进行有效评估,也未能充分考虑结构在施工期不同受力阶段之间的非线性时变效应。因此,本文依托国内首条矩形盾构隧道,在现场监测试验结果的基础上,建立基于施工全过程的衬砌结构受力分析方法,其能够全面考虑施工过程对衬砌结构受力的动态影响以及结构自身在施工过程中的动态变化,进而获取结构在施工过程中的真实受力状态,以期研究结果为相关隧道结构的设计提供指导和借鉴。
1 工程背景
1.1 工程概况
上海虹桥临空11-3地块地下连接通道工程采用矩形盾构法施工,为国内首条大断面矩形盾构隧道。盾构隧道长约30 m,隧道的覆土厚度约为6 m,隧道纵断面如图1所示。
1.2 地质情况与结构设计
工程地质纵断面如图2所示。隧道穿越的地层主要为③2灰色砂质粉土与④灰色淤泥质黏土。工程地质物理力学参数见表1。
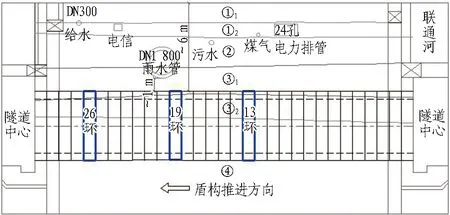
图1 隧道纵断面图
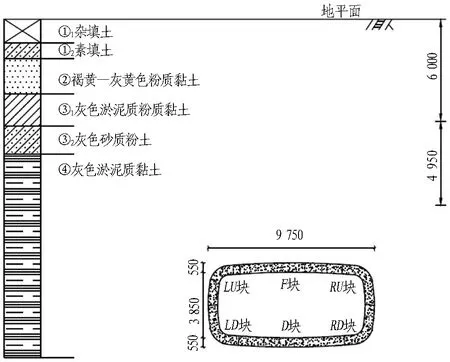
图2 工程地质纵断面图(单位: mm)
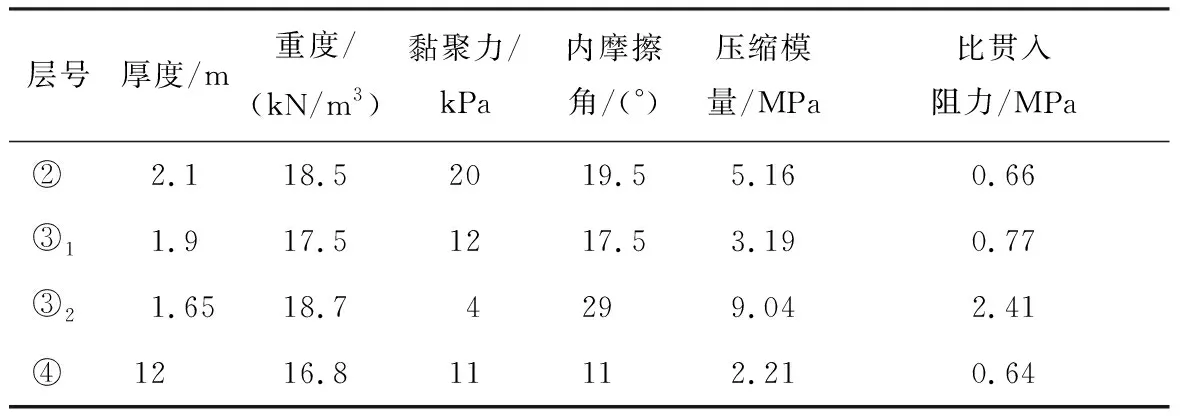
层号厚度/m重度/(kN/m3)黏聚力/kPa内摩擦角/(°)压缩模量/MPa比贯入阻力/MPa②2.118.52019.55.160.66③11.917.51217.53.190.77③21.6518.74299.042.41④1216.811112.210.64
隧道采用通缝拼装方式,衬砌结构的形式及尺寸如图2所示。结构外轮廓尺寸为9.75 m×4.95 m,管片厚度为0.55 m,环宽1.0 m。管片间共布置28根纵向螺栓,每个管片块间接缝处布置4根环向螺栓。隧道采用钢筋混凝土组合管片结构,管片内外表面及端面均为钢板,内部充填混凝土。
1.3 盾构推进过程
隧道工程的施工流程可概括为盾构推进—出土—管片吊运—管片拼装—螺栓施拧及复紧的不断循环的过程。根据隧道施工的流程,可将某一管片环由推进、拼装到其脱出盾尾定义为一个施工循环。该施工循环包括若干施工工序,在每一施工工序下,盾尾附近各环管片所处的状态如图3所示。
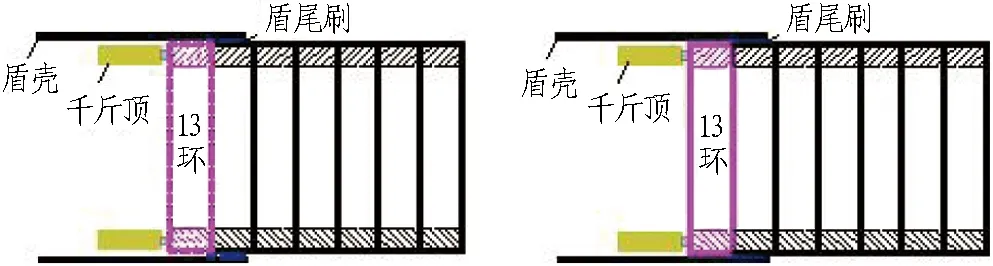
(a) 13环推进 (b) 13环拼装、螺栓施拧
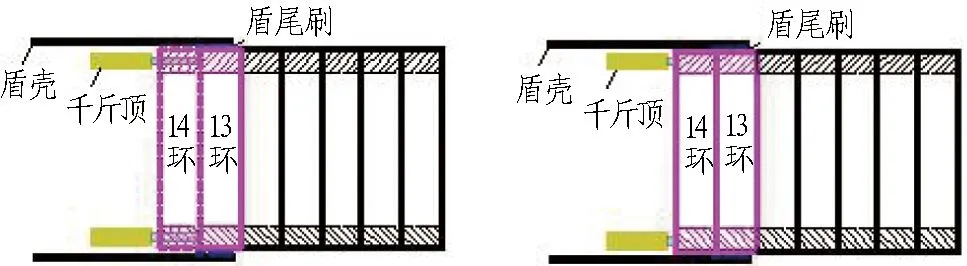
(c) 14环推进,13环接触盾尾刷 (d) 14环拼装、螺栓施拧

(e) 15环推进,13环逐渐脱出盾尾,14环接触盾尾刷 (f) 15环拼装、螺栓施拧
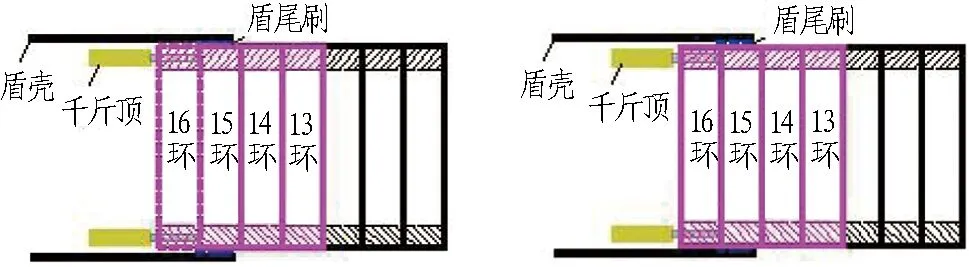
(g) 16环推进,13、14环逐渐远离盾尾,15环接触盾尾刷 (h) 16环拼装、螺栓施拧
图3每一施工工序中盾尾附近各环管片的状态
Fig. 3 Status of different segments near shield end during every construction procedure
1.4 现场监测试验
本次试验共选取了3个测试断面,具体位置见图1蓝色标记的管片环。主要测试内容包括施工过程中的结构外荷载、管片内外表面应变和连接螺栓轴力,具体测试方案和试验结果分析见文献[8]。
2 基于施工全过程的衬砌结构受力分析方法
2.1 分析原理
根据矩形盾构隧道结构的现场试验结果可知,衬砌结构在施工期的受力可划分为自重阶段、脱出盾尾阶段、同步注浆阶段和稳定荷载阶段;结构在施工期处于弹性受力范围;结构的荷载、位移边界条件随受力阶段的变化而变化[8]。根据管片单体抗弯试验和纵缝接头试验结果,管片本体抗弯刚度、纵缝接头的抗剪刚度和转动刚度随内力的变化而变化。
在现场试验结果的基础上,结合施工力学理论,首先可以将盾构隧道衬砌结构在施工期的受力行为归结为非线性时变力学的范畴,即考虑衬砌结构在施工过程中刚度、约束和荷载的非线性时变特征,施工过程中其对衬砌结构的最终受力状态有不可忽视的影响;同时,由慢速时变结构力学理论,按照离散性时间冻结的近似处理方法,将结构做时不变的静力分析,即无任何加速度作用[9-12]。
基于施工全过程的盾构隧道衬砌结构受力分析方法的原理可归纳为: 结构在施工期的4个主要受力阶段之间具有非线性时变效应,即结构的刚度、荷载和约束在4个阶段均是变化的、非线性的,因此,应分别建立结构受力模型进行受力分析;在其中任一阶段,结构荷载与约束不变,但仍需考虑结构刚度随结构内力的变化情况,结构受力计算采用静力分析方法。
在整个施工期的结构受力分析中,采用增量法理论,即分析结构当前阶段的受力状态时需将上一阶段的结构受力状态作为初始条件,最后通过增量叠加得到衬砌结构在施工过程中的最终受力状态以及全过程中的最不利受力状态。
衬砌结构受力分析计算的基本方程为
(1)
式中:i为1、2、3和4,分别表示自重阶段、脱出盾尾阶段、同步注浆阶段和稳定荷载阶段; [K]为结构的整体刚度矩阵;EI为管片本体的抗弯刚度;kv、kθ和ks分别为纵缝接头抗剪刚度、纵缝接头转动刚度和结构底部约束弹簧刚度; [Δ]为结构的结点位移矩阵; [F]为结构的结点荷载矩阵。
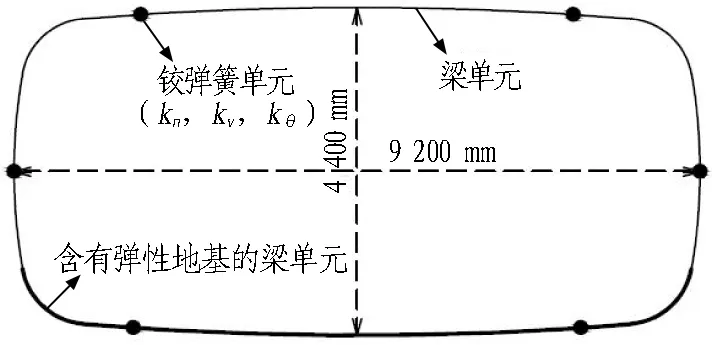
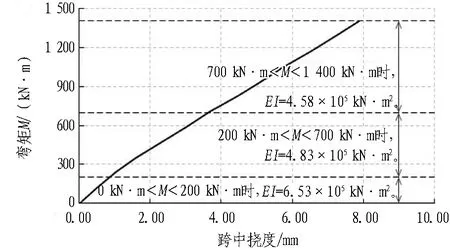
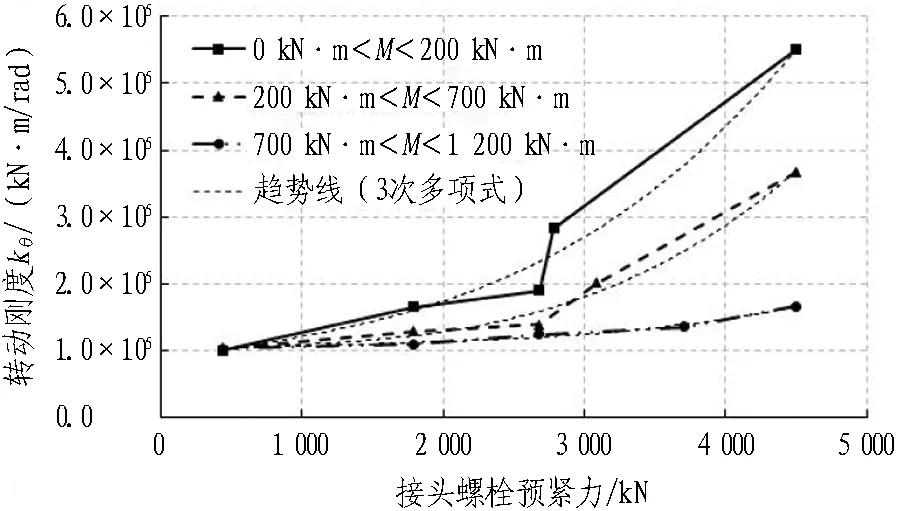
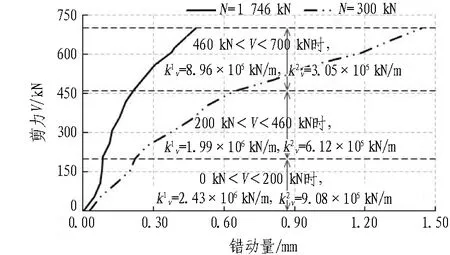
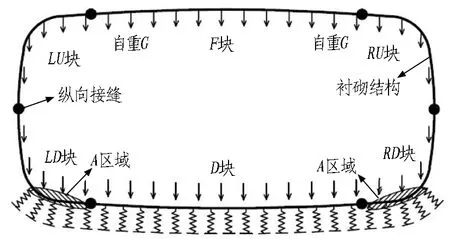
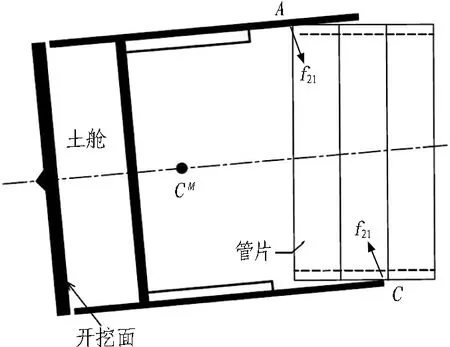
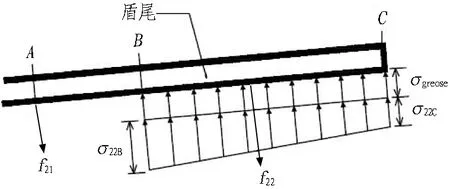
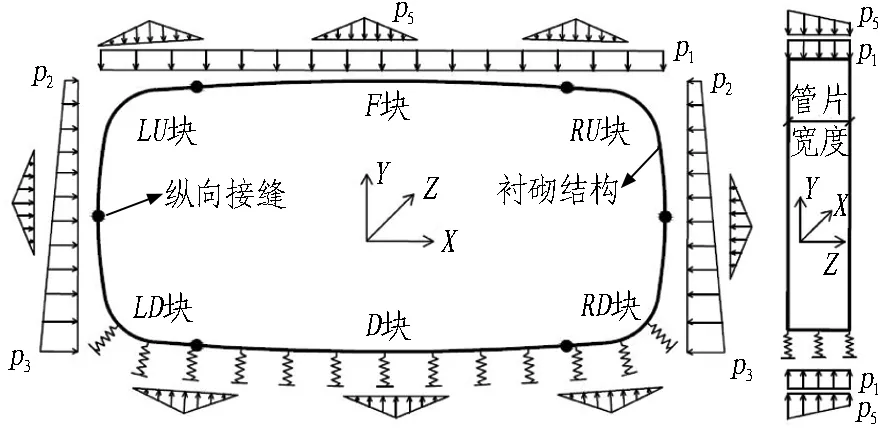
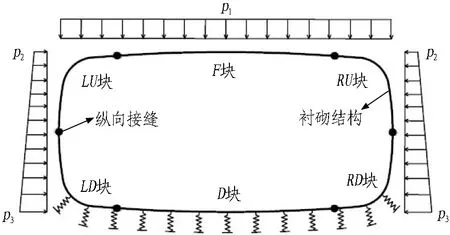
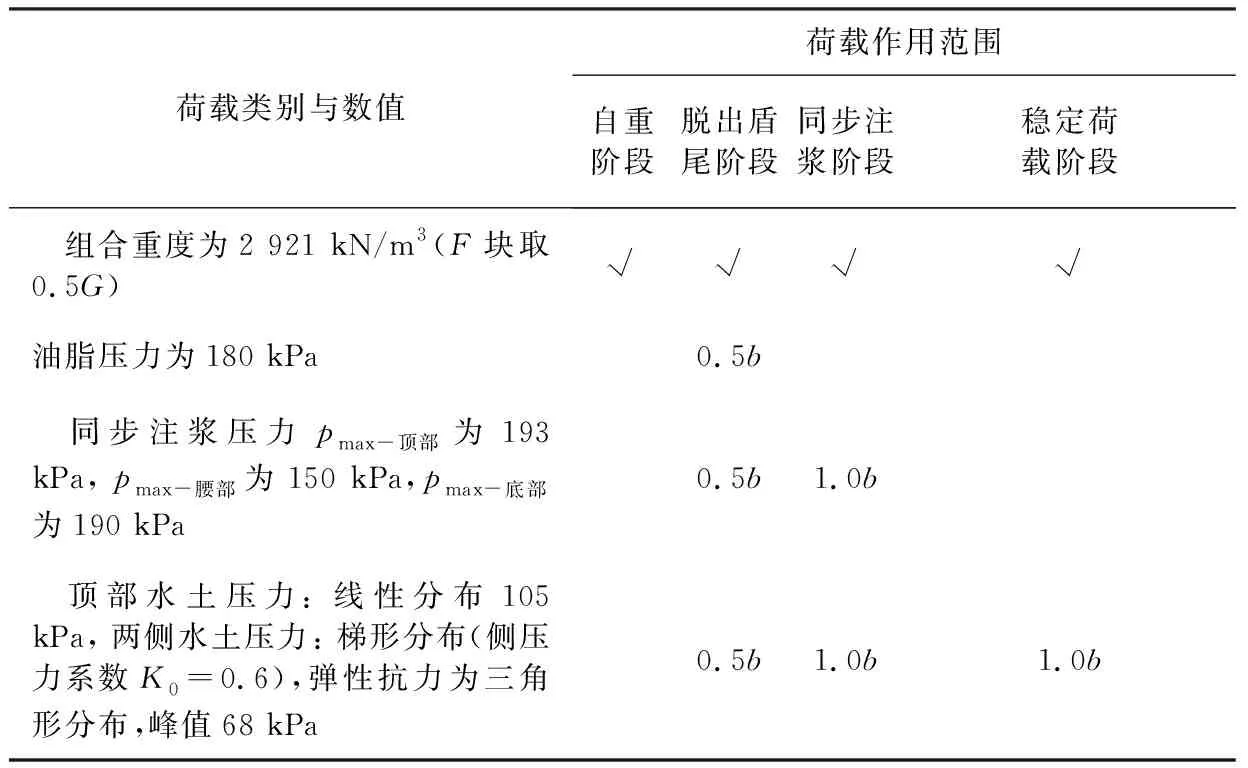
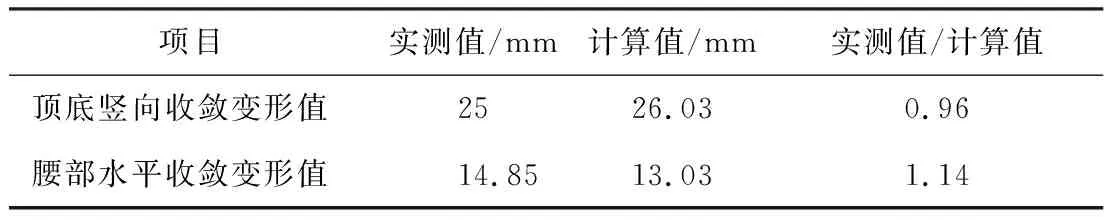
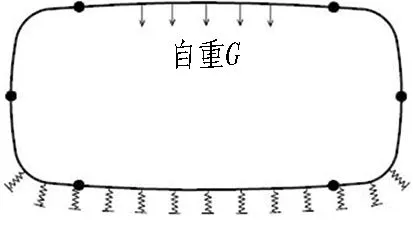
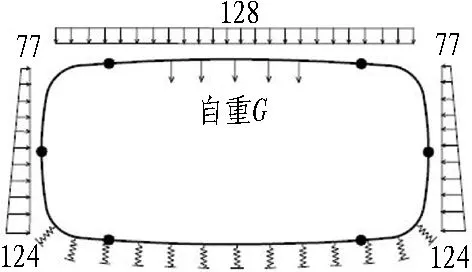
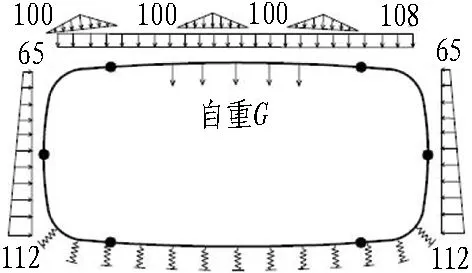
根据管片单体抗弯试验与纵缝接头试验可知,管片本体抗弯刚度EI、纵缝接头抗剪刚度kv、转动刚度kθ均与结构内力有关,并通过分析得到其与结构内力呈相关的多折线刚度变化曲线(不同结构内力段对应不同的刚度常量)。因此,在2个受力阶段之间,根据需要将荷载增量{ΔF}细分为n(1,2,3,…)步,并根据式(1)依次进行结构受力计算。为保证在计算步m(m=1,2,3… 根据结构受力分析原理,采用有限单元法进行相关计算,隧道衬砌结构采用梁-弹簧模拟。有限元模型如图4所示。管片采用梁单元模拟,其中,结构底部采用含有弹性地基的梁单元,以模拟实际地基土对结构的反作用力;结构的其余部分则采用普通梁单元模拟。 kn、kv和kθ分别为沿X轴的轴向刚度、沿Y轴的剪切刚度和绕Z轴的转动刚度。 图4衬砌结构有限元模型 Fig. 4 Finite element model of lining structure 对于管片块之间的纵向接头,采用铰弹簧单元模拟,其3个弹簧刚度(沿X轴的轴向刚度kn、沿Y轴的剪切刚度kv和绕Z轴的转动刚度kθ)可模拟纵向接头在实际受力中的转动和变形。 参照矩形盾构隧道管片单体抗弯试验,可得到管片抗弯刚度,如图5(a)所示;参照纵缝接头试验,可得到纵缝接头转动刚度和剪切刚度的折线模型,分别如图5(b)和图5(c)所示。 (a) 不同弯矩范围内管片抗弯刚度EI (b) 不同弯矩范围内纵缝接头转动刚度 (c) 不同剪力范围内纵缝接头抗剪刚度 图5结构相关刚度的折线模型 Fig. 5 Broken linear model of structural stiffness 由图5可知,管片本体抗弯刚度与其所受实际内力密切相关,不同的内力范围对应不同的抗弯刚度值;纵缝接头转动刚度和剪切刚度与接头连接螺栓初始预紧力以及接头实际内力密切相关,不同螺栓预紧力以及不同内力范围对应不同的刚度值。矩形盾构隧道结构受力计算时的相关结构刚度根据图5中的多折线模型进行取值。 2.3.1 自重阶段 自重阶段衬砌结构在环向主要受到自身重力以及千斤顶顶力在管片环环缝处引起的摩擦力。根据管片环的拼装过程及其受力特点,可以建立衬砌结构在自重阶段的荷载模型,如图6所示。 图6 衬砌结构在自重阶段的荷载模型 在自重阶段,衬砌结构所受的荷载仅为其自身重力。LD块和RD块的A区域部分与整个D块与相邻环之间的摩擦阻力用弹簧来模拟(文献[13]中采用含有地基反力系数的虚拟弹簧来模拟千斤顶纠偏控制等对隧道管片的支撑效果),作为衬砌结构的位移边界条件,弹簧的刚度可根据纵向千斤顶的顶力以及管片之间的摩擦力确定。为简化计算,对于LD块和RD块的非A区域部分、LU块和RU块,其与相邻环之间的摩擦阻力不再考虑。对于F块,采用折减自重的方法考虑其与相邻环之间的摩擦作用,折减系数根据纵向千斤顶顶力以及管片之间的摩擦力确定。 2.3.2 脱出盾尾阶段 设计条件下,盾尾钢丝刷与管片之间存在一定间隙,两者之间无挤压作用,钢丝刷的刚度较小。当盾构推进以及同步注浆进行一段时间后,随着盾尾刷的间隙内不断充填注浆材料,注浆材料逐渐硬化,盾尾刷的刚度逐渐增加。当盾构调整姿态发生扭转或者变形时,管片外表面和盾尾刷之间的间隙减小,引起盾构壳体和盾尾刷挤压管片外表面;同时,盾构姿态的改变也会引起盾尾钢丝刷的变形,在管片外表面产生不均匀的作用力;此外,钢丝刷之间的油脂压力也会在管片外表面产生作用力[14-15]。盾尾变形在管片外产生的作用力如图7所示[15]。图7中,f21为盾构姿态调整引起的作用在管片上的不等压力,为集中力,其反作用力作用在盾尾内表面;f22为作用在管片上的盾尾钢丝刷变形产生的压力和油脂压力的合力,其反作用力作用在盾尾内表面;σ22B和σ22C分别为盾尾刷变形作用在B单元和C单元的压力,其大小与钢丝刷刚度及变形量有关;σgrease为2排钢丝刷之间的油脂压力。 (a) f21 (b) f22 Fig. 7 Forces exerted by deformation of shield tail on lining surface 根据现场试验结果,在脱出盾尾阶段,尚处于盾尾内的部分结构外表面作用有油脂压力以及盾壳和盾尾刷的挤压作用力;已脱出盾尾的部分结构外表面作用有同步注浆压力和水土压力。盾尾内钢丝刷在纵向的跨度为0.5 m左右,因而取衬砌结构沿宽度方向一半已脱出盾尾、一半仍处于盾尾内的状态作为衬砌结构在脱出盾尾阶段的最不利受力状态,结构荷载模型如图8所示。 p1、p2和p3均为水土压力;p4和p5分别为油脂压力和同步注浆压力。 图8脱出盾尾阶段结构荷载模型 Fig. 8 Load model of lining structure in stage of segment going out of shield tail 针对仍处于盾尾内的结构部分,其外表面作用油脂压力p4。根据现场试验的测试结果,除部分测点外,其他测点所测油脂压力比较接近,因而可将受力模型简化为沿结构环向均匀分布的模型,在结构宽度方向,也采用均匀分布形式;除油脂压力外,还有盾尾刷的挤压力,而盾尾刷挤压力与盾尾姿态有关,且其大小及作用位置灵活多变,故在本受力模型中不再考虑该作用力。 对于已脱出盾尾的结构部分,其外表面作用有同步注浆压力p5和部分水土压力p1、p2和p3。 2.3.3 同步注浆阶段 同步注浆阶段即衬砌结构刚脱出盾尾到其沿轴向距离盾尾1 m的过程,结构外荷载主要为同步注浆压力和水土压力,结构荷载模型如图9所示。 图9 同步注浆阶段结构荷载模型 Fig. 9 Load model of lining structure in synchronous grouting stage 根据文献[8]现场试验的测试结果可知,同步注浆阶段衬砌结构环向各荷载测点的测试值均随时间呈先增大后减小并趋于平稳的趋势。该阶段各测点的峰值均大于后续稳定阶段相同位置的全部水土压力值,该阶段内趋于平稳的荷载值与后续稳定阶段相同位置处的全部水土压力相当,即消散掉的压力值为注浆压力。因此,本阶段中水土压力的大小和分布形式均采用后续稳定阶段水土压力的大小和分布。 对于同步注浆压力的分布模式,文献[16]中提到盾尾注浆的浆液在土体中呈半圆柱面扩散,且任意半径r处的注浆压力与半径r呈负相关;国际隧道协会工作报告中推荐在二维横断面上同步注浆压力采用等腰三角形分布形式。结合上述提到的2种注浆压力分布模式,最终采用半“正四棱锥”的分布形式,即以同步注浆孔作为注浆压力峰值点,在平行于管片环的平面(图9中X-Y平面)上呈等腰三角形分布,在垂直于管片环的平面(图9中Y-Z平面)上也呈等腰三角形分布,在2个方向上距离注浆孔为b(作用宽度)时,注浆压力降为0。 文献[8]中现场试验得到的同步注浆压力在纵向的作用范围基本为2个管片宽度(单环管片宽1 m)。因此,同步注浆压力作用宽度b取2 m。单环管片上注浆压力p5的分布如图9所示。本节仅分析单个同步注浆孔处注浆压力的分布模式,单环管片上同步注浆荷载分布点位应根据实际盾构设备进行确定,壁后注浆的注浆压力分布模式不在本文进行讨论分析。 2.3.4 稳定阶段 荷载稳定阶段即衬砌结构脱出盾尾一段距离后,结构外荷载趋于稳定的过程。根据现场试验的结果,该阶段衬砌结构外荷载与运营阶段的理论计算水土压力基本吻合。因此,该阶段衬砌结构的受力模型可取运营阶段的结构荷载模型,如图10所示。结构底部的地层反力采用弹性地基弹簧模拟,弹簧刚度可根据衬砌结构所在地层的地基刚度确定。 图10 荷载稳定阶段的结构荷载模型 2.4.1 结构外荷载取值 由现场试验结果[8]得到不同受力阶段结构外荷载的取值见表2。结合结构数值模型及模型参数的取值方法,将本文建立的基于施工全过程的受力分析方法应用到背景工程中,进行结构在施工期的受力分析。 2.4.2 结构收敛变形和内表面钢板应变 分别从结构收敛变形和内表面钢板应变2个方面将衬砌结构在施工期不同受力阶段的理论计算值与现场试验的实测值进行对比分析。 2.4.2.1 结构收敛变形 将现场试验[8]测得的衬砌结构在脱出盾尾前后的竖向、水平向收敛变形值与理论计算值进行对比,结果见表3。 表2 不同受力阶段结构外荷载取值 表3结构收敛变形实测值与理论计算值对比 Table 3 Comparison of structural deformation between measured values and calculation values 项目实测值/mm计算值/mm实测值/计算值顶底竖向收敛变形值2526.030.96腰部水平收敛变形值14.8513.031.14 由表3可以看到,结构竖向和水平向收敛变形的实测值与计算值的误差在15%内。 2.4.2.2 结构内表面钢板应变 由现场试验测得脱出盾尾阶段、同步注浆阶段和稳定阶段下结构控制截面的内表面钢板应变。控制截面①—⑧位置如图11所示。 Fig. 11 Distribution of controlled section of internal force of lining structure 部分关键控制截面处,衬砌结构在3个受力阶段的内表面应变实测值与理论计算值对比见表4。 表4 结构内表面钢板应变的实测值与理论计算值对比 由表4可以看出,不同受力阶段关键控制截面处结构内表面钢板应变的实测值与理论计算值的误差基本在15%以内。 综上所述,本文建立的基于施工全过程的结构受力分析方法是合理的,可应用于工程实际并反映出结构的实际受力状态。 3.1.1 传统设计方法下结构的荷载工况 传统设计方法即基于概率的极限状态设计方法,对结构在不同作用效应组合下的响应取包络,然后进行相应的截面设计和验算。在计算衬砌结构荷载时,结构覆土取6 m,土体重度为18 kN/m3,水土合算,侧压力系数为0.6,地面超载为20 kPa,考虑结构自重,弹性地基系数取5 000 kN/m3。同步注浆与二次注浆的附加压力均按等腰三角形分布,峰值为100 kPa,影响范围为2 m。管片截面组合抗弯刚度取8.21×105kN·m2,组合轴向抗压刚度取2.64×107kN,组合重度取29.21 kN/m3。纵缝接头仅考虑其转动变形,转动刚度根据接头试验测得,取1.7×105kN·m/rad。 进行计算的结构荷载工况主要包括自重工况、正常使用工况(侧压力系数0.6)、同步注浆工况和二次注浆工况。传统设计方法各工况的荷载模型如图12所示。 (a) 自重工况 (b) 同步注浆工况 (c) 正常使用工况 (d) 二次注浆工况 图12传统设计方法各工况的荷载模型(单位: kPa) Fig. 12 Structural load conditions in conventional design method(unit: kPa) 3.1.2 本文方法与传统设计方法对比 根据现场试验的测试结果[8]可知,衬砌结构在脱出盾尾前后2种设计方法下衬砌结构变形对比见表5。测试环在脱出盾尾阶段、同步注浆阶段和稳定阶段下的结构部分控制截面的内表面应变见表6。 在以上实测数据的基础上,分别采用本文建立的衬砌结构设计方法(以下简称本文分析方法)和传统设计方法进行施工过程各受力阶段的结构响应分析,并与实测数据进行对比。传统设计方法中无脱出盾尾阶段的设计工况,根据现场试验结果[8],本文分析方法中脱出盾尾阶段为结构在施工期的最不利受力阶段之一。因此,可采用传统设计方法中各工况的包络值减去自重作用下的变形值得到的差值作为脱出盾尾阶段的变形增量。 表5 2种设计方法下衬砌结构变形对比 Table 5 Comparison of lining structure deformation between two design methods 施工阶段变形方向变形量/mm本文方法传统方法现场实测本文方法与现场实测的比值传统方法与现场实测的比值脱出盾尾阶段(增量)顶底竖向δv26.0316.2925.001.040.66腰部水平向δh13.039.5414.850.880.64 表6 2种设计方法下内表面应变对比 Table 6 Comparison of internal surface strain between two design methods 施工阶段控制截面内表面应变/(×10-6)本文方法传统方法现场实测本文方法/现场实测传统方法/现场实测脱出盾尾阶段①492475③-364-374-3431.061.09⑦-367-384-3001.221.28同步注浆阶段①454455 5020.900.91③-333-346-3670.910.94⑦-344-356-3600.960.99稳定荷载阶段(正常使用工况)①321422 4000.801.06③-236-328-2700.871.21⑦-237-329-2550.931.29 由表5可以得到,在脱出盾尾阶段,采用本文分析方法得到的结构变形值与实测结果的误差在12%以内,而采用传统设计方法得到的结构变形值与实测结果的误差达到35%左右。由表6可知,在部分控制截面处,本文分析方法与传统设计方法得到的结构内表面应变与现场实测数据的平均误差分别在11%和14%左右。 对于结构变形,在自重阶段、同步注浆阶段和稳定荷载阶段(正常使用工况)2种设计方法得到的结果如图13所示。 从图13中可以看到,在自重阶段和稳定荷载阶段,2种设计方法得到的结构变形差别较小;而在同步注浆阶段,本文分析方法得到的结构竖向变形和水平向变形分别为传统设计方法计算值的1.46倍和1.32倍,两者差别较大,和脱出盾尾阶段类似。 图13 2种设计方法下衬砌结构变形对比 Fig. 13 Comparison of structural deformation between two design methods 对于结构内表面应变,2种设计方法在脱出盾尾阶段和同步注浆阶段下的计算值较接近,而实际作用到衬砌结构上的同步注浆压力要大于常规设计方法下所考虑的压力值,原因在于本文设计方法所采用的受力模型中考虑了实际土体在结构两侧产生的弹性抗力作用。在稳定荷载阶段(正常使用工况),与传统设计方法相比,本文分析方法计算所得的结构内力偏小,原因在于本文设计方法所采用的受力模型中的水土荷载为现场试验的实测荷载值,结构两侧存在一定的土体弹性抗力,且常规设计方法考虑了地面超载。 综上所述,衬砌结构在施工中的非线性时变效应能更好地反映整个施工过程中结构实际所处的受力状态及其变化情况。本文分析方法计算得到的脱出盾尾阶段和同步注浆阶段下结构变形和内力均明显大于稳定荷载阶段,即脱出盾尾阶段和同步注浆阶段均是结构在施工期的不利受力阶段。 衬砌结构由管片拼装组成,管片在接头处靠螺栓连接在一起,接头的转动和剪切滑动主要受连接螺栓约束,及时施加螺栓预紧力可在结构受力早期提供较大的接头刚度。同时,在实际施工过程中,未能及时将接头螺栓施拧至设计预紧值将导致结构变形超过设计值。 将螺栓预紧力作为单一影响因素,分析其对衬砌结构在施工过程中内力和变形的影响作用。矩形盾构隧道实际施工中的纵缝接头螺栓预紧力为1 164 kN[8],取螺栓预紧力分别为500、2 000、4 000 kN。根据基于施工全过程的衬砌结构设计方法,对不同螺栓预紧力下结构在施工过程中的受力进行对比分析。 3.2.1 不同螺栓预紧力对衬砌结构变形的影响分析 脱出盾尾阶段,衬砌结构的顶底竖向变形绝对值、腰部水平向变形绝对值随螺栓预紧力的变化曲线如图14所示。 图14 结构变形随螺栓预紧力的变化曲线 Fig. 14 Variation curves of structural deformation with bolt pre-tightening force 由图14可以看出,衬砌结构变形随螺栓预紧力的增大而减小,减小的速率随螺栓预紧力的增大而降低,说明增大螺栓预紧力可以有效降低衬砌结构的变形,当螺栓预紧力过大时,其降低衬砌结构变形的作用将弱化。 由计算可得,与螺栓预紧力为500 kN时的结构变形相比,螺栓预紧力为4 000 kN时结构顶底竖向变形量与腰部水平向变形分别降低了23.23%和45.75%,说明螺栓预紧力对腰部水平向变形的影响比对顶底竖向变形的影响大。 3.2.2 不同螺栓预紧力对衬砌结构内力的影响分析 脱出盾尾阶段,结构控制截面处内力随螺栓预紧力的变化曲线如图15所示。 (a) 顶底块中心截面①和截面⑤ (b) 结构右侧截面②、③、④ Fig. 15 Variation curves of internal force with bolt pre-tightening force in controlled sections 由图15可知,结构顶底中心2个控制截面处的弯矩(正弯矩)随螺栓预紧力的增加呈缓慢减小的趋势,衬砌结构右侧3个控制截面的弯矩(负弯矩)随螺栓预紧力的增加呈缓慢增加的趋势。 由计算可知,与螺栓预紧力为500 kN时的结构弯矩相比,螺栓预紧力为4 000 kN时结构顶底中心的2个控制截面①和⑤的弯矩分别降低了4.73%和1.19%,结构右侧的3个控制截面②、③和④的弯矩分别增加了7.81%、9.07%和11.34%。说明螺栓预紧力对结构两侧负弯矩区的影响比对结构顶底正弯矩区的影响大。 衬砌结构顶底中心的2个控制截面与结构两侧的3个控制截面处的轴力随螺栓预紧力的增加基本没有变化,说明螺栓预紧力的改变对衬砌结构轴力基本没有影响。 本文建立了基于施工全过程的矩形盾构隧道结构受力分析方法,并以实际隧道工程为例与传统设计方法进行了比较分析,主要结论如下: 1)矩形盾构隧道中,施工期脱出盾尾阶段和同步注浆阶段均是结构的不利受力阶段。 2)基于全过程的结构受力分析方法能更好地反映整个施工过程中结构实际所处的受力状态(结构本身特性、外部约束及其响应)以及变化情况。 3)增大螺栓预紧力可有效降低衬砌结构变形,螺栓预紧力过大时,其降低衬砌结构变形的作用将弱化;螺栓预紧力的变化对腰部水平向变形的影响比对顶底竖向变形的影响大;螺栓预紧力的变化对结构两侧负弯矩区的影响比对结构顶底正弯矩区的影响大,对结构轴力基本没有影响。 本文中,脱出盾尾阶段结构受到的盾尾挤压力的作用模式和大小尚需要进一步的研究;另外,基于施工全过程分析方法中的迭代计算过程需要程序化,以增强其在类似实际工程中的适用性。2.2 衬砌结构有限元分析模型的建立与参数设置
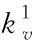
2.3 衬砌结构不同受力阶段的荷载模型

2.4 背景工程验证

3 讨论分析
3.1 与传统设计方法比较分析


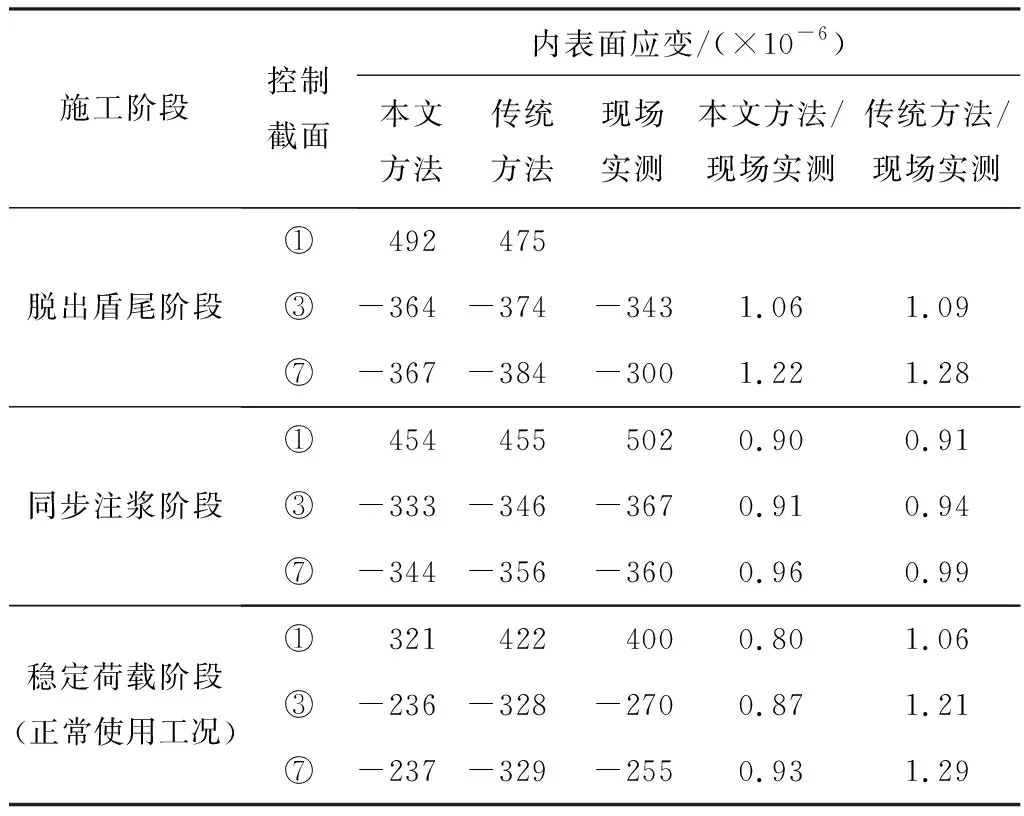
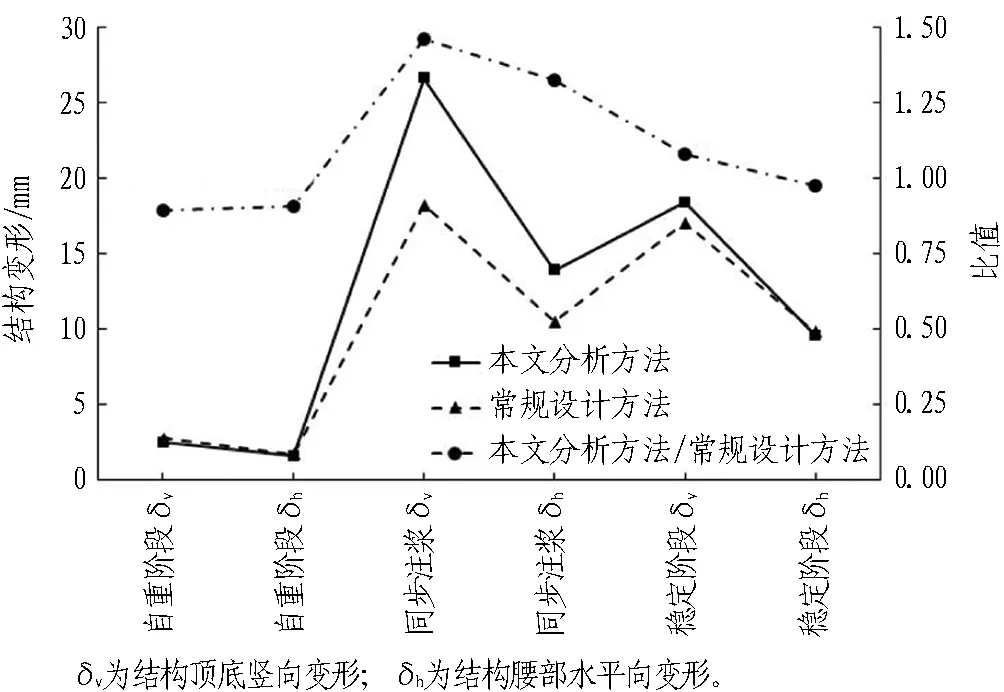
3.2 关键影响因素分析
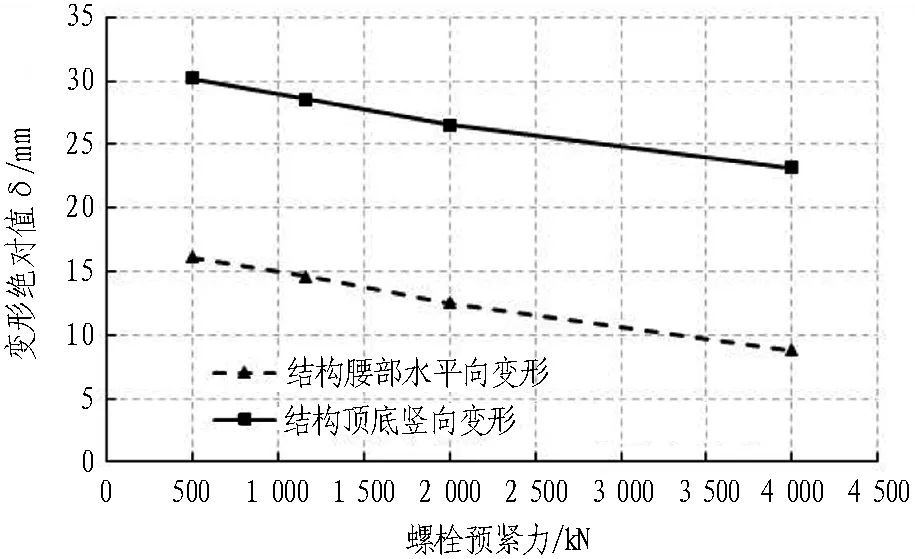
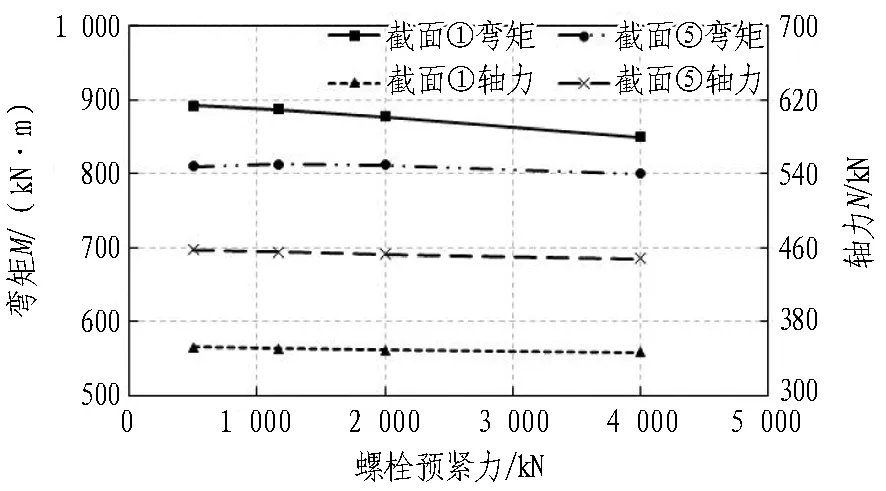
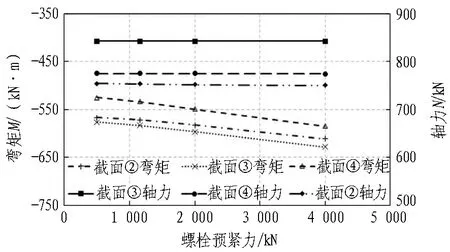
4 结论与讨论

