Spark云计算平台下的结构物理参数辨识

骆剑彬， 姜绍飞， 任 晖， 赵 剑

(福州大学 土木工程学院,福州 350116)

随着经济的发展和科技的进步，许多大型工程如超大桥梁、超高层建筑、海洋平台结构等得以兴建，他们在长期服役的过程中，环境侵蚀、材料老化和荷载的长期效应、疲劳与突变等灾害因素的藕合作用将不可避免地发生损伤积累必然导致结构物理参数如刚度、质量、阻尼发生改变，从而在极端情况下引发灾难性的突发事故[1]。因此对大型工程结构进行结构健康监测和结构损伤识别具有极其重要的意义。结构健康监测系统和损伤检测是目前保证大型结构安全运行的主要措施。然而，随着大型复杂结构安装的传感器数量越来越多，结构健康系统产生的监测数据随着时间推移趋于海量化[2]，传统的结构分析计算方法遇到了很大的困难：首先大型复杂结构的结构健康监测系统在长期、连续的监测中，采集的数据量十分巨大；其次由于监测手段的日趋丰富,监测数据的种类越发多样化;另外,系统对数据处理的速度要求也不断提高,再加上结构健康监测系统本身的缺陷比如测量精度低、系统可靠性差等问题,使得如何能够快速、有效的分析数据成为目前结构健康监测中最重要的研究课题之一。而云计算的出现，恰好为解决这一课题提供了新的思路和方法。

云计算是一种按需取用计算资源的模式，这种模式提供可用的、便捷的、按需的网络访问和可配置的计算资源共享池，只需进行少量的管理工作，就可以快速获得大量计算资源[3]。目前云计算方法已成功运用于金融、医疗、电网、地理信息等领域[4]，近年部分学者尝试将云计算方法应用到土木工程领域。朱晓斌等[5]在Hadoop平台上使用并行聚类算法对桥梁结构状态演化进行评估，并与传统的串行聚类算法进行比较。Ventura等[6]探讨了云计算的并行性能，并应用于高层建筑设计和非线性动力分析。陈亮[7]利用MATLAB并行和分布式计算工具箱对ITD模态参数识别任务进行了云计算模拟，实现了并行计算程序的单机和多机云中分布式计算。段梦凡[8]在Hadoop平台上实现了悬梁的二维矩形网格划分的有限元分析的计算过程。林菁淳等[9-10]将传统的时序分析方法与Hadoop平台的Map/Reduce编程模型相结合，提出基于云计算的结构损伤检测新方法，通过两层刚架结构仿真模拟和三层框架结构实验验证了该方法的可行性、有效性和精确性。

云计算平台主要包括Hadoop、Apache Spark等技术。其中Hadoop云计算技术从2003年发展至今，它的MapReduce[11]编程模型得到广泛推广。但MapReduce计算过程的数据存储依赖本地磁盘和分布式文件系统(HDFS)，面对诸如多粒子群(PSO)等智能优化算法的迭代运算时，磁盘存取将占用大量时间开销，大幅降低算法整体执行效率。2009年由加州大学伯克利分校的AMPLab实验室最初开发了Apache Spark，它是一个围绕速度、易用性和复杂分析构建的大数据处理框架，并于2010年成为Apache的开源项目之一，可用来构建大型的、低延迟的大数据分析系统。Apache Spark克服了MapReduce在迭代式计算的不足，能够很好地解决MapReduce不易解决的问题[11]。基于此，本文尝试引入Apache Spark云计算平台的弹性分布式数据集(RDD)，将传统多粒子群协同优化(MPSCO)算法结构物理参数辨识进行分布式并行化改进，提出Spark云计算平台下改进并行化多粒子群协同优化(IPMPSCO)算法的结构物理参数辨识方法，并在8节点的云计算集群上对一个30层框架数值试验和一个7层钢框架试验进行结构物理参数辨识，最后进行算法的性能比较。

1 基本原理

1.1 Apache Spark技术

Spark能够很好地解决迭代运算和交互式运算，主要是因为Apache Spark引入了弹性分布式数据集RDD(Resilient Distributed Datasets)，它是一个有容错机制，可以被并行操作的数据集合，能够被缓存到内存中，而不必像MapReduce那样每次都从HDFS上重新加载数据。据Apache官方测试，Spark运行逻辑回归算法的计算速度是Hadoop的10倍～100倍。

Spark通过转换和动作对RDD数据集进行操作，从而得到所需RDD数据集。与Map和Reduce不同的是，Spark提供广播和累加器两种受限的共享变量，可以像分布式内存系统一样提供全局地址空间接口，提高了数据的共享性[12]。Spark 丰富全面的数据集运算操作，除了Map和Reduce操作，还增加了过滤、抽样、分组、排序、并集、连接、分割、计数、收集、查找等80多种算子，并合理地划分为Transformation(变换)和Action(动作)两大类。利用这些算子，能够方便地建立起RDD的有向无环图(Directed Acyclic Graph,DAG)计算模型，将所有操作优化成DAG图[13]。本文用到的主要操作运算如下。

1)extFile。首先从HDFS或其他文件系统导入原始数据集，并转换成RDD数据集。

2)flatMap。按照用户编写映射程序逻辑将原始RDD数据集映射成多个输出RDD数据集的(key,value)键值对。

3)filter。去掉错误的键值对。

4)Map。按照用户编写Map映射函数程序逻辑，对步骤2)成的(key,value)键值对重新进行映射，形成新的(key,value)键值对。

5)Reduce。将数据按照key分组后，调用用户编写函数进行处理，每组返回一个键值对。

6)Join。根据步骤3)和步骤4)产生的RDD数据集键值对，产生新RDD数据集。

1.2 改进的并行化多粒子群协同优化算法(IPMPSCO)

受鸟群觅食行为的启发，Eberhart和Kennedy于1995 年共同提出了粒子群优化算法。随后，国内外学者纷纷对其展开了各种研究和改进。其中，多粒子群协同优化算法(MPSCO)兼顾了种群的多样性和收敛速度，使粒子陷入局部最优的可能性大大降低而受到广泛的关注[15]。对MPSCO算法进行并行化改进可以采用粗粒度和细粒度2 种不同的方式，王保义等[16]采用粗粒度并行化思想，设计实现基于Spark和IPPSO_LSSVM的短期分布式电力负荷预测算法，本文在此基础上进一步改进优化，提出改进的并行化多粒子群协同优化算法IPMPSCO(Improved Parallel MPSCO)，进一步加快粒子群收敛速度和提高精确度。并行化MPSCO算法的核心思想是将每个粒子的速度更新、位置更新和计算适应值的过程组成一个独立的并行单元，因此n个粒子构成n个独立的并行单元，用Apark Spark进行并行处理,如图1所示。算法的具体步骤如下：

步骤1 随机初始化产生m个子种群，每个子种群包括n个粒子并将这些子种群分为两层: 上层有1个子种群，下层有m-1个子种群，并将粒子随机平均分配到k个并行处理单元。

步骤2 各个并行处理单元计算各粒子的适应度值，将个体极值位置及其相应的适应度值记录为pbest和pbestval，将各子种群的最优个体位置及相应的适应度值记录为gbesti和gbestvali，i= 1，2，…，m，同时在共享区上将整个种群中最优个体位置及相应的适应度值记录为gbest和gbestval。

步骤3 各个并行处理单元分别根据式(1)和(2)更新上层子种群和下层子种群。

(1)

(2)

式中:k表示当前进化代数；vi和zi分别表示第i个粒子的速度和位置；pi表示第i个粒子经历的最佳位置；pg和pgi分别表示整个种群和第i个粒子所在子种群经历的最佳位置；r1和r2为[0,1]之间的随机数；c1和c2为学习因子；w为惯性权重。

步骤4: 计算更新后各个并行处理单元各粒子的适应度值，如果更好，则相应更新pbest、pbestval、gbest、gbestval、gbesti和gbestvali。

步骤5 判断是否达到了预设的结束条件( 一般为获得足够好的适应度值或者达到了预设的最大进化代数)，如果没有则返回步骤3; 反之则停止迭代并输出搜索到的最优解。

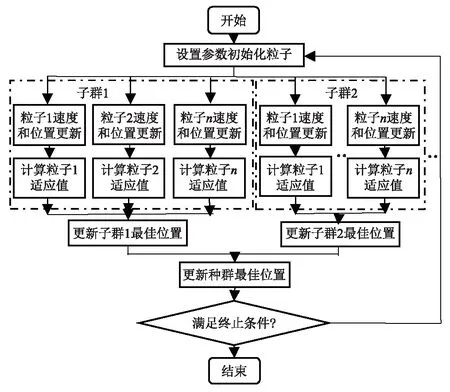
图1 改进的并行化多粒子群协同优化算法流程Fig.1 Process of IPMPSCO

2 基于Apache Spark的结构物理参数辨识

结构物理参数辨识可以转化为参数优化问题，即使现场或者试验室实测的结构响应与相应数值模型预测的响应之间的误差最小：

(3)

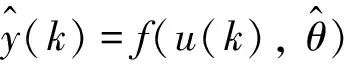
文献[17]得出基于动力时程响应(位移、速度或加速度)的适应度函数在框架结构物理参数辨识中具有良好的抗噪性和峰值特性。由于加速度数据实时性较好，较为可靠，现有结构健康监测系统大多采集加速度数据，故本文选用基于加速度建立的适应度函数见式(4)。

(4)

式中：Fa为适应度函数，θ是待辨识结构参数向量，amea(i,j)和anum(i,j)分别表示结构实测与数值模型预测的第i时刻第j测点加速度响应，N为测点总数，L为测量数据总长度。也就是说，将结构的N个测点总长为L的加速度数据逐一与预测的加速度响应值进行相差的平方累加，获得适应度函数。

为了直观观察算法收敛情况，将基于加速度的适应度函数进行倒数，见式(5)。此时，当适应度函数值越大，表示相应粒子所代表的结构物理参数越接近于真实值。

(5)

在建立基于加速度的适应度函数时，对于线性结构计算数值模型预测加速度响应值采用Newmark积分法[18]。Newmark积分法求解结构动力时程响应的基本思想为：给定初始时刻的位移、速度、加速度及整个时程的外部激励后，通过逐步迭代求得后续时刻的位移、速度和加速度，其主要基于如下假定：

vi+1=vi+[(1-γ)ai+γai+1]Δt

(6)

(7)

式中：si、vi和ai分别为第i时刻的位移、速度和加速度；si+1、vi+1和ai+1分别为第i+1时刻的位移、速度和加速度；Δt是时间步长；γ和β是决定求解精度和稳定性的参数，当γ=1/2、β=1/4时，算法为无条件稳定，称为Newmark常平均加速度法。

另外，第i+1时刻的结构运动方程可表达为：

Mai+1+Cvi+1+Ksi+1=Fi+1

(8)

式中：M、C和K分别为结构的质量矩阵、阻尼矩阵和刚度矩阵；Fi+1为第i+1时刻作用于结构的外部激励。

当给定初始时刻结构的位移s0、速度v0和加速度后a0，通过联合式(6)～(8)就可以求解整个时程的预测加速度响应值。

系统物理参数识别分为质量已知、质量未知两种情况，本文针对质量已知展开研究。通过运用分布式内存计算框架Apache Spark，在质量知的情况下，利用并行化算法对结构物理参数包括结构刚度(或弹性模量、惯性矩)和阻尼进行优化，即IPMPSCO算法的输入为一个向量[k1,k2, …,kn,ζ1,ζ2, …,ζm]。其中，实现该算法的RDD数据集数据格式如下：

(ID,ColonyID,x,v,ffit, (Pi,ffiti), (Pg,ffitg), (Pu,ffitv))

(9)

式中：ID为粒子群编号；ColonyID为子群编号；x=(x1,x2, …,xn)为粒子的当前位置向量；v=(v1,v2, …,vn)为粒子的当前速度向量；ffit为粒子的当前适应度值，通过适应度函数计算得出；(Pi,ffiti)为个体经历的最佳位置信息向量，Pi=(xi1,xi2, …,xin)为个体经历的最佳位置，ffiti为个体经历的最佳适应度值；同理(Pg,ffitg)和(Pu,ffitv)分别对应子群经历的最佳位置信息向量和整体粒子群经历的最佳位置信息向量。

通过对RDD数据集操作实现本文并行化算法的执行步骤如下。

1) 初始化粒子群,在取值范围内随机生成粒子群，包括初始位置和初始速度，并按照预先计划子群数量确定确定粒子ColonyID；

2) 按照式(1)、式(2)更新粒子位置向量和速度向量，通过适应度函数(5)计算粒子的个体适应度值ffit并更新(Pi,ffiti)；

3) Map操作，以ColonyID为key值，其他数据为value,构成(key,value)键值对;

4) Reduce操作，获取各个子群的最佳适应度值和对应最优解，产生(key,value)键值，其中key是ColonyID,value是(Pg,ffitg)；

5) Join操作，将步骤4)获取键值对与步骤3)中键值对连接，再进行一次Map，更新(Pg,ffitg);

6) Map操作，以ID为key，其他数据为value重新构造(key,value)键值对；

7) Reduce操作，获得整体粒子群最佳适应度值和对应最优解，产生(key,value)键值，其中key是ID,value是(Pu,ffitv)；

8) Join操作，将步骤7)获取键值对与步骤6)中键值对连接，再进行一次Map，更新(Pu,ffitv);

9) 判断是否迭代结束，是则输出(Pu,ffitv), 否则返回步骤2)进行下一轮迭代。

3 数值试验验证

3.1 剪切型线性框架结构模型

本文以一个30层剪切型线性框架结构数值模型为例验证该方法，简化模型如图2所示。假设模型各层质量为m1=m2=…=m29=3.78 kg，m30=3.31 kg，层间刚度值为k1=k2=…=k30=375 kN/m，前两阶阻尼比ζ1和ζ2均为2%。随机激励F作用在结构的顶层，采样频率取1 000 Hz，采样时间取5 s，对原始加速度数据分别取无噪声和35 db、25 db的高斯白噪声。

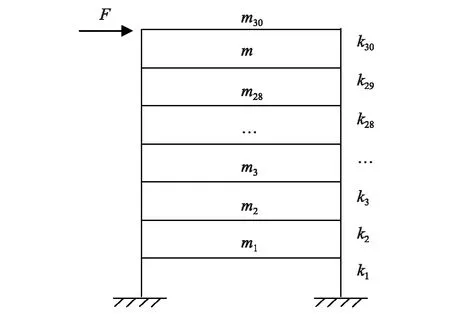
图2 30层框架结构简化模型Fig.2 30-story frame structure simplified model

文中所有的实验都是在实验室搭建的基于Ubuntu操作系统的Apache Spark集群平台上运行的。其中1个节点计算机作为Master节点，也作为work节点。为了验证多台计算机的并行性，每台计算机只分配一个worker节点。首先将计算任务分配到Master节点，然后再由Master 节点将计算任务分配给worker节点。实验环境中节点的属性信息，如表1所示。

表1 集群信息表

3.2 辨识模型的建立

(1)选取辨识数值模型的加速度和随机激励的时间段；在结构质量已知的情况下，设定待优物理参数为[k1,k2, …,k30,ζ1,ζ2]，参数搜索范围取真实值的0.5倍～2倍；设定IPMPSCO参数: 种群数量m=10，子种群粒子数n=200、最大迭代次数Imax=2 000、学子因子c1=c2=2，此外假定惯性权重w在[0.9,0.4]之间线性变化，同时，Newmark时间步长取0.02 s，每个时间段取500个采样点，除第一个时间段初始位移、速度、加速度取0外，其余时间段的初始响应根据上个时间段的识别结果确定。

(2)运行基于Apache Spark的IPMPSCO算法，将粒子随机平均分配到各个并行处理单元。各个并行处理单元分别计算粒子速度、位置和适应度值。

(3)输出最优辨识结果，为了尽量避免偶然现象的影响，取10次辨识结果的平均值作为最终的辨识结果。

3.3 辨识结果与讨论

3.3.1 辨识结果

本文采用平均相对误差(MAPE)作为评价识别算法的指标，如式(10)所示。

(10)

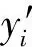
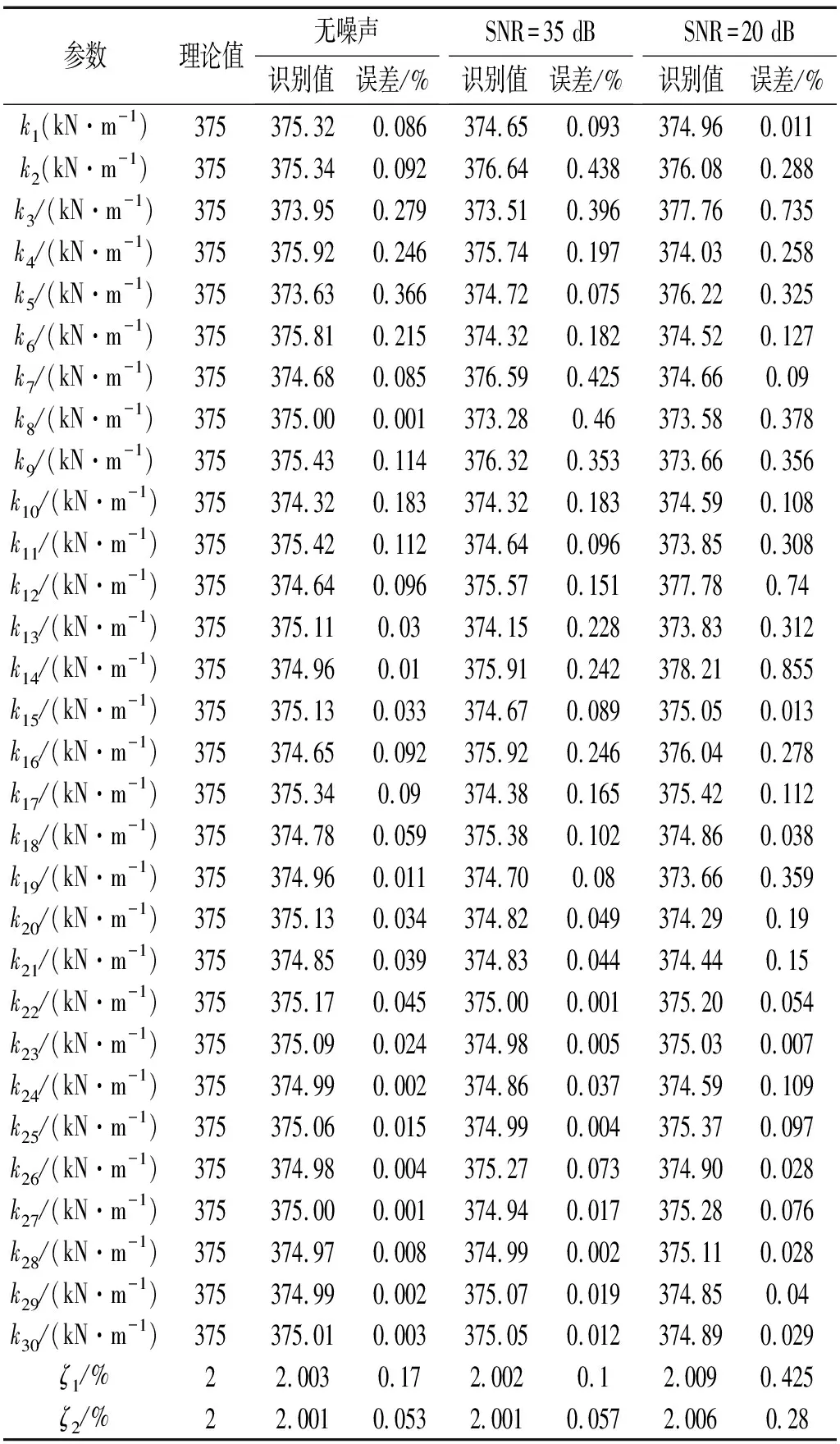
表2 不同噪声水平下的辨别结果(质量已知)

分别向结构各层加速加数据和随机激励中添加高斯白噪声，不同噪声水平时的识别结果如表2所示。从表2中可以看出，在无噪声情况下，辨别结果最好；在SNR=35 db时，辨别结果不比无噪声情况下差； 在SNR=20 db时，辨别结果误差有所变大。同时获得三个不同噪声水平下的收敛曲线，如图3所示。由收敛曲线可知，迭代到800次，三条曲线都能获得较高的精度。总之，虽然结构层间刚度和阻尼比的辨别精度随噪声水平的增大而有所下降，但总体上仍然具有较高的辨别精度。

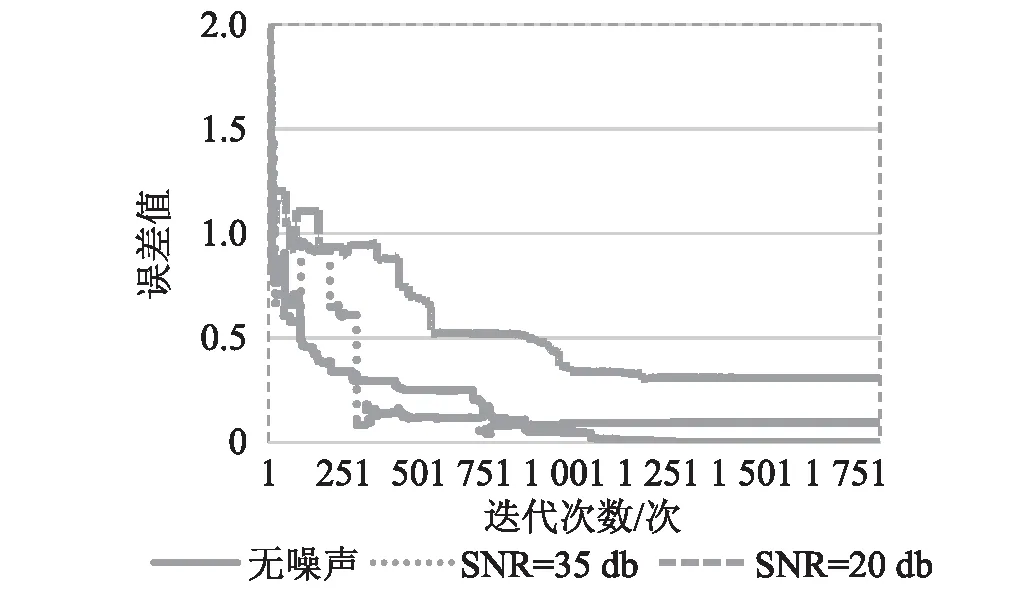
图3 不同噪声水平下收敛曲线对比Fig.3 The convergence curves with different noise levels

为了分析测量数据的长度对IPMPSCO算法辨别性能的影响，分别利用1倍、2倍、4倍和8倍基本周期(T)长度的加速度数据进行辨别，这里采用1～30层的加速度数据，并考虑SNR=35 db的情况，识别结果见表3。从表3中可以看出，在测量数据长度为1T时，辨识误差最大；在测量数据长度为2T、4T、8T时，辨识误差没有显著差别。总之，总体上结构层间刚度的辨别精度随着测量数据的增加而提高，理论上随着测量数据的无限增加，精度将概率趋近1，但充分考虑辨别精度和计算成本的话，在实际应用时可以选取2倍～4倍结构基本周期长度的时程响应数据进行计算。

3.3.2 性能分析

本文采用加速比Sn来测试IPMPSCO算法的并行性能。加速比是衡量并行系统或程序并行化的性能和效果的指标[19]，如式(11)所示，其中Ts为算法的单机执行耗时，Tc为算法的集群执行耗时。

Sn=Ts/Tc

(11)

为了分析IPMPSCO算法的并行运算能力，本文将用100倍、200倍和400倍基本周期(T)长度的加速度数据进行识别，分别在集群节点个数为2个、2个和8个的云平台上运行，计算Sn，加速比如表4所示。在实际应用中，并行系统的算法加速比很难达到线性增长，从表可知，随着数据量增大，加速比更接近线性。因此IPMPSCO算法采用云计算平台保持原有良好精度的情况下，能够缩短了辨识时间，满足海量高维监测数据的结构物理参数辨别的性能要求。

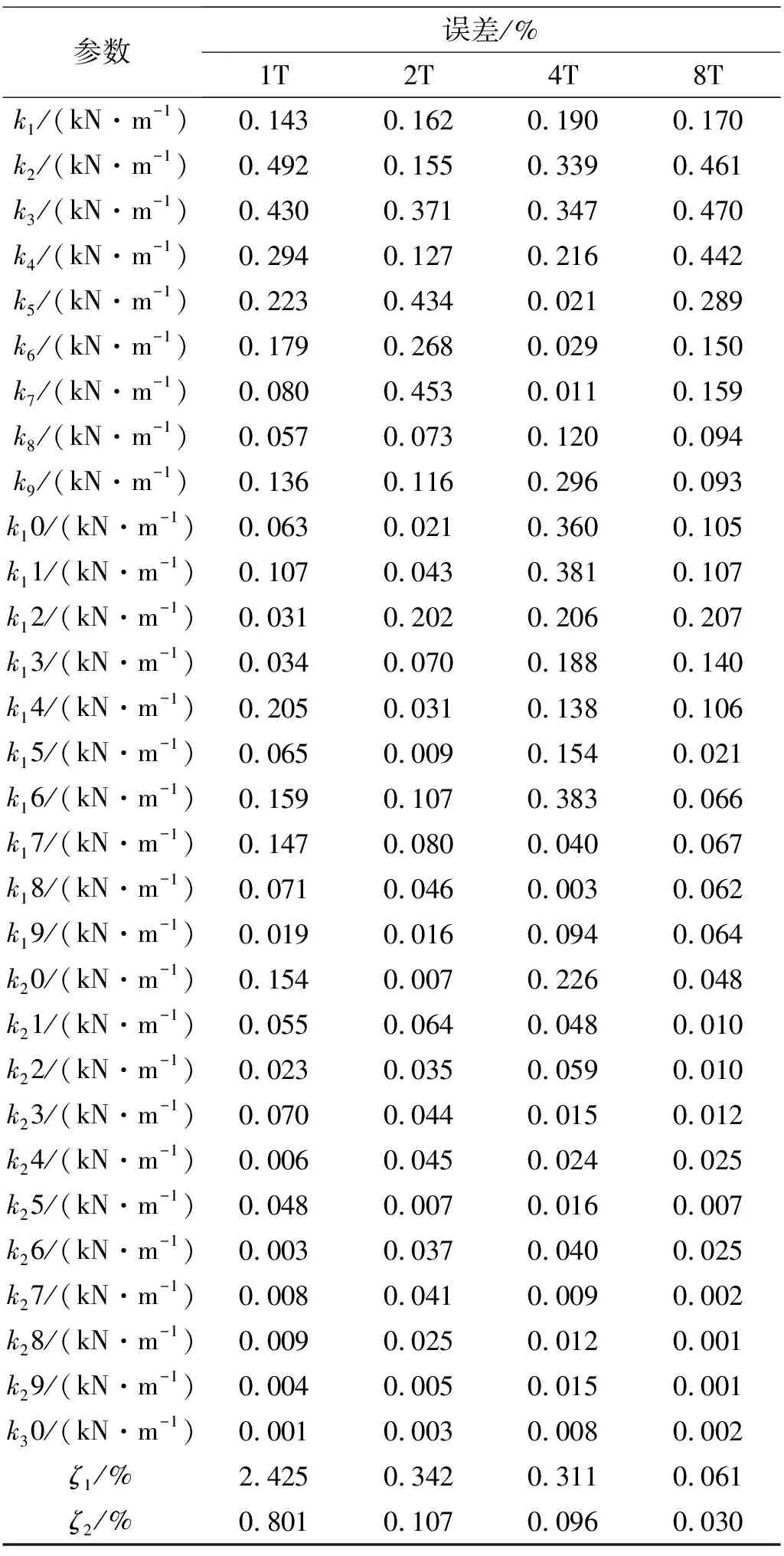
表3 不同测量数据长度时的辨别结果(质量已知)

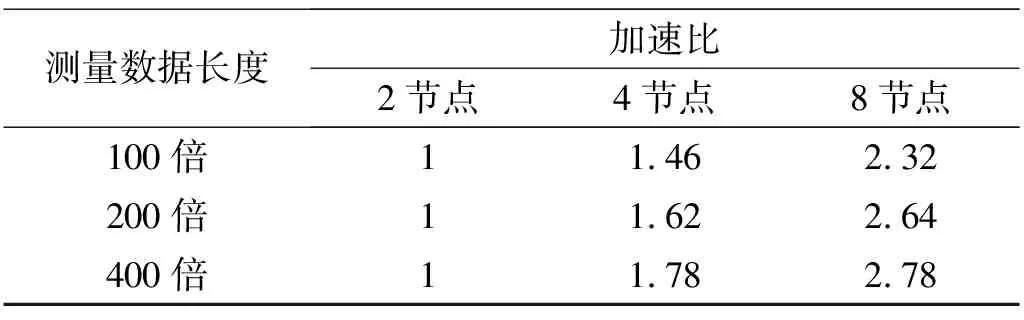
表4 不同测量数据长度时的加速比

4 框架结构模型试验

4.1 钢框架结构模型

实验模型是一个7层、2跨×1的钢框架缩尺模型，如图4所示。模型平面尺寸为0.4 m×0.2 m，高1.412 5 m。框架构件采用热轧300 W级钢材(fy= 300 MPa)。梁柱截面性质如表5所示。在模型顶层跨处进行激振，每层记录加速度响应，采样频率5 000 Hz。

图4 实验室模型装置图Fig.4 Setup of experimental steel frame model

参数梁柱截面尺寸/mm25×25×325×4.6截面面积A/m2264×10-6115×10-6惯性矩I/m42.17×10-82.03×10-10杨氏模量E/Pa206×109206×109体密度ρ/(kg·m-3)7 8507 850

4.2 辨识结果与分析

7层钢框架试验模型进行结构物理参数辨识，建模与识别过程见3.1至3.2节。辨识结果见表6。

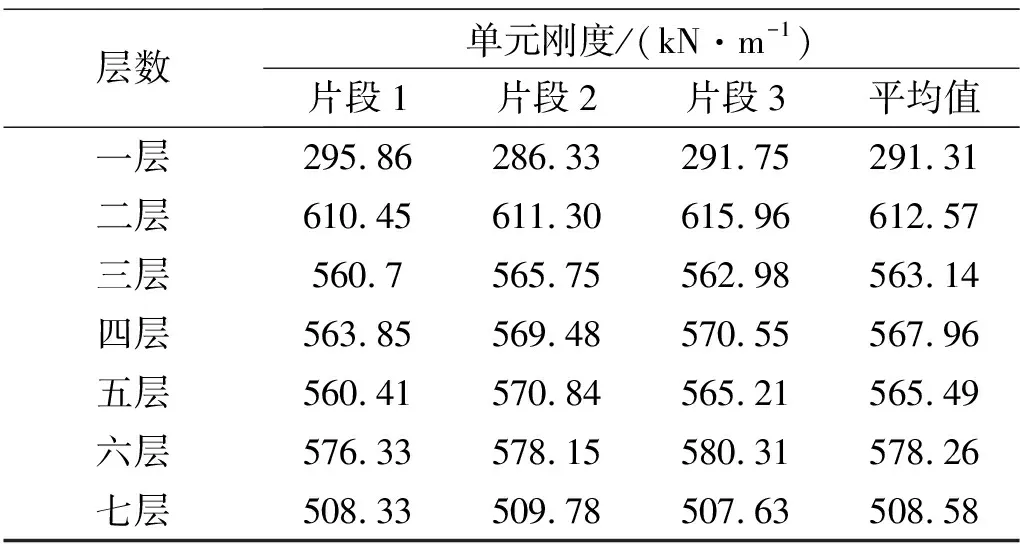
表6 单元刚度辨识结果

从表6可以看出，通过IPMPSCO算法能够稳定辨识出不同工况状态下的结构层间刚度参数，验证了本文所提辨识方法对试验模型物理参数辨识的准确性和稳定性。

5 结 论

(1)提出了一种基于Spark云计算平台IPMPSCO结构物理参数辨识算法，该算法通过增加云计算集群数量保持原有良好精度的情况下，缩短了辨识时间，同时有效利用了大量闲置主机的运算能力。

(2)在8节点的云计算集群上对一个30层框架数值试验和一个7层钢框架试验进行结构物理参数辨识。结果表明，本文所提方法对框架数值试验的结构层间刚度和阻尼比的辨别精度随噪声水平的增大而有所下降,随着测量数据的增加而提高,但总体上仍然具有较高的辨别精度；对钢框架试验能够稳定辨识出不同工况状态下的结构层间刚度参数。

随着中国防震减灾土木工程信息化和智能化的快速发展，带来了数据量激增和数据维度不断提高的问题，单机运算和存储能力已不能满足结构损伤识别对效率和精度要求。本文只是将云计算平台应用于结构物理参数辨识进行尝试性试验，因此，在云计算平台上的应用还存在效率优化等问题。