单比特压缩感知帧定时同步

王 维，卿朝进，万东琴，阳庆瑶

西华大学 电气与电子信息学院，成都 610039

1 引言

作为数字通信系统的重要组成部分，帧定时同步是一直以来的研究热点[1-2]。帧定时同步的性能直接影响通信系统性能，错误的帧定时同步将造成数据信息难以恢复。然而，日益增加的高数据速率需求使得帧定时同步面临挑战，是当前通信系统亟待解决的问题之一[3-5]。

现有的相关法[6]、最大似然法[7-11]等帧定时同步方法的接收信号采样速率需满足采样定理。随着人们对高数据速率需求的日益增加，急切需要高采样速率的模拟数字转换器（Analog-to-Digital Converter，ADC）。然而，高的采样速率导致系统高的能量消耗，造成ADC设计难度增加。文献[2]提出了一种基于压缩感知（Compressed Sensing，CS）的帧定时同步方法。相对于现有非压缩感知帧定时同步方法，文献[2]方法降低了系统的采样速率，在一定程度上减少了系统的能量消耗，缓解了ADC设计难度。相对于压缩感知技术，“单比特压缩感知”[12]仅保留观测值的符号信息，其量化过程通过简单的电平比较器实现，可进一步降低系统的能量消耗，降低模拟数字转换器的设计难度。

为此，在文献[2]的基础上，本文将单比特压缩感知技术引入到帧定时同步中，提出了一种基于单比特压缩感知的帧定时同步方法。提出方法首先将接收信号映射到帧定时变换域，并在帧定时变换域对接收信号进行单比特的压缩采样；随后，根据二进制迭代硬阈值（Binary Iterative Hard Thresholding，BIHT）算法[13]，利用采样到的比特流重构出用于帧定时同步的定时度量；最后，根据相关法帧定时同步准则[6]，搜索重构到的定时度量，找到帧定时同步的索引位置。分析与仿真结果表明，相对于压缩感知帧定时同步方法，在相同的正确同步概率情况下，提出方法所用比特数更少；同时，提出方法的量化过程仅需电平比较器，降低了ADC设计难度。

2 单比特压缩感知

本文将单比特压缩感知技术引入到帧定时同步中。下面，首先对单比特压缩感知技术进行介绍。

单比特压缩感知技术在2008年由Boufounos和Baraniuk提出[12]，其量化模型为：

其中，x是N×1的矢量，Φ是M×N的测量矩阵，y是对观测值进行单比特量化后的 M×1的矢量，即y=[ ]

y1,y2,…,yMT，sign(·)表示符号函数。根据文献[7]，单比特压缩感知的重构过程可表示为：

其中，Y=diag(y)表示以矢量y的元素为对角元素的对角阵。

目前，基于单比特CS的重构算法主要有固定点连续（Fixed Point Continuation，FPC）算法[14]、二进制FPC[12]、匹配符号追踪（Matching Sign Puisuit，MSP）算法[15]、限制步长收敛（Restricted Step Shrinkage，RSS）算法[6]、二进制迭代硬阈值（Binary Iterative Hard Thresholding，BIHT）算法等。在上述算法中，BIHT算法是一种一阶算法，是从标准CS重构算法中的迭代硬阈值（Iterative Hard Thresholding，IHT）算法[16]发展而来的。该算法因其运行速度快，信号重构效果好，收敛性强等特点[13]，而被广泛应用。鉴于此，本文采用BIHT算法对帧定时同步的压缩采样信号进行重构处理。

3 单比特压缩采样帧定时同步方法

3.1 单比特压缩采样

根据文献[17]，Zadoff_Chu序列是一种恒包络零自相关（Constant Amplitude Zero Auto-Correlation，CAZAC）序列，具有恒定的幅值特性、良好的自相关属性以及良好的互相关属性。因此，本文采用Zadoff_Chu序列作为训练序列。

根据文献[1]，在采用非压缩感知帧定时同步方法的情况下，接收机接收到的信号矢量r可以被表示为：

其中，r为N×1的接收信号矢量。c=(c0,c1,…,cL-1)表示长度为L的训练序列，d=(dL,dL+1,…,dN-1)表示长度为 N-L的数据信息；cd=(c0,c1,…,cL-1,dL,dL+1,…,dN-1)表示c和d的连接，T(·)表示循环移位运算，m表示待估计的帧的起始位置，即接收信号采样序列与本地训练序列进行滑动相关，然后搜索相关峰来获得；n=(n0,n1,…,nN-1)为高斯噪声，其组成元素ni，i=0,1,…,N-1是均值为0，方差为σ2的高斯随机变量，图1为帧定时同步的起点示意图。

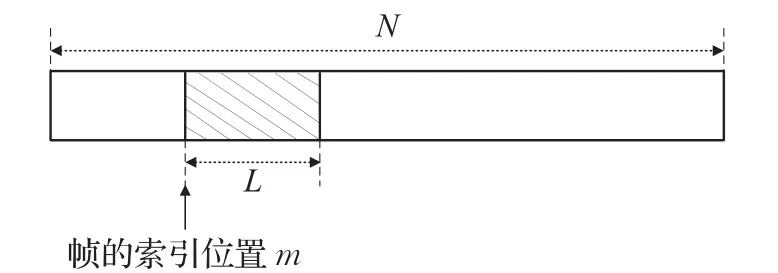
图1 帧定时同步的起点示意图

根据文献[1]，定时度量可表示为：

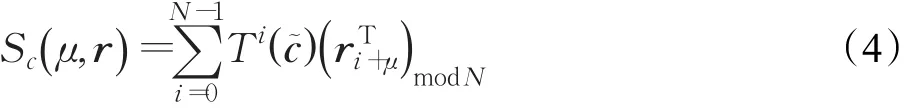
式

（4）中，上标“T”表示转置运算，(·)modN表示每次对接收信号截取长度N。取

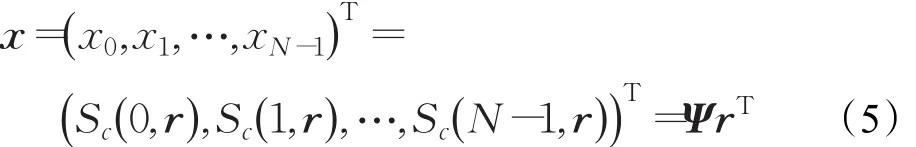
其中

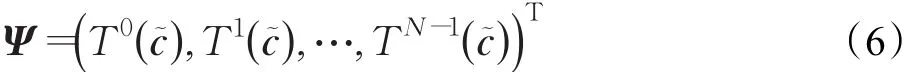
c~由c和1×( N-L )的零向量串接形成，即

矢量x由定时度量Sc(0 ,r),Sc(1 ,r),…,Sc(N -1,r)组成，定时度量的幅度值 |Sc(0 ,r)|,| Sc(1 ,r)|,…,| Sc(N -1,r)|只有少部分非零，其余的为零，是典型的稀疏信号，或可压缩信号。根据单比特压缩感知原理，单比特压缩采样可表示为：

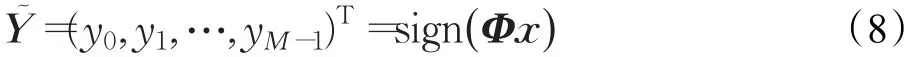
式（8）中，Y~表示单比特量化后的测量矢量。

3.2 定时度量重构

本文采用BIHT算法对帧定时同步的定时度量进行重构处理。根据文献[14，18-19]，目标函数为ΦT(Y~-sign(Φxl))，将重构定时度量的估计值映射到l2范数超球面上({ x ∈RN:‖x‖2=1} )。信号初始值取x0=0，则BIHT算法的迭代计算公式为：

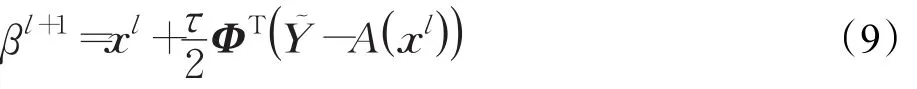
其中，τ表示控制梯度下降步长的可调参数，Y~表示测量值的符号，A(xl)表示当前信号估计值xl的测量值符号，即A(xl)=sign(Φ xl)。然后，通过硬阈值函数获取信号估计值的K稀疏表征信号，即

BIHT算法重构定时度量的模型可表示为：

其中，[·]_表示负函数，u⊙v表示u与v的点积，(u ⊙v)i=uivi，ui与vi均为标量。通过计算单边l1范数最小，可以确保得到 yˉ⊙(Φ x )≥0。

定时度量的重构过程如下所述[18]：

输入：单比特观测值Y~，观测矩阵Φ，映射A，最大迭代次数lmax。

步骤1初始化x0=0，迭代次数l=0。

步骤2梯度计算βl+1=xl+ΦT(Y~-A(xl))。

步骤3硬阈值运算并映射到单位球上xl+1=ηK(βl+1)，（其中，ηK(·)为非线性算子，它将保留βl+1的前K个最大元素，其余元素置为零）。

步骤4计算nnz=‖Y~ - A(xl+1)‖0，比较符号不一致的个数。

步骤5更新迭代次数l=l+1。

步骤6若l＜lmax且nnz＞0时，返回执行步骤2；否则执行步骤7。

步骤7输出xl+1=U(xl+1)，其中U(v)=v‖v‖2。

根据上述算法，当重构的定时度量与原来采样值符号一致或者迭代次数达到最大时，BIHT算法终止迭代。

3.3 帧同步

根据相关法帧定时同步准则，在对定时度量进行重构之后，搜索重构到的矢量x~中幅度最大值的索引，找到帧定时同步的索引位置m~，即：

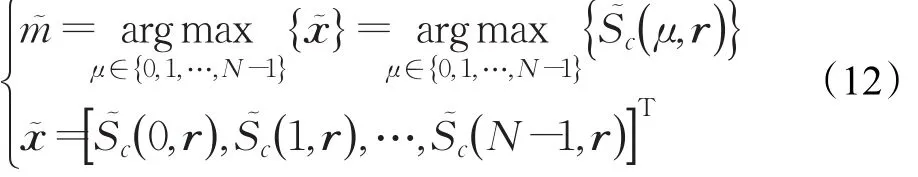
相对于文献[2]方法，由于单比特压缩，提出方法的量化过程仅需要简单的电平比较器，这将会降低模拟数字转换器设计的难度。

4 实验仿真及分析

为验证提出的单比特压缩感知帧定时同步方法的有效性，给出相应的数值仿真。根据文献[20]，信噪比（Signal Noise Ratio，SNR）可表示为：

其中，Ps表示信号的功率，Pn表示噪声的功率。

4.1 提出方法与文献[2]和文献[6]方法性能比较

为了验证提出方法的有效性，本节将提出方法与文献[2]和文献[6]方法性能同时进行比较。其中，文献[2]为传统压缩感知帧定时同步方法，文献[6]为传统的“相关法”（非压缩感知帧定时同步方法）。文献[6]所述的“相关法”，其接收信号采样速率需满足奈奎斯特采样定理；相对于文献[2]和本文提出方法的压缩采样，文献[6]方法的ADC设计更为困难。

4.1.1 正确同步概率的比较

在采样所需的比特数相同的情况下，实验验证提出方法相对于文献[2]方法（传统压缩感知帧定时同步方法）和文献[6]方法（传统的“相关法”，即非压缩感知帧定时同步方法）的有效性。其中，文献[6]和文献[2]方法均采用16 bit量化器（采样序列的实部和虚部分别进行16 bit量化）。由于没有压缩采样，文献[6]方法所需的比特数为32N；文献[2]方法所需的比特数为32M′（其中M′为文献[2]方法测量次数）。考虑提出方法与文献[2]方法所需比特数目相同，有M=32M′（其中M为所需比特开销，即提出方法测量次数）。考虑文献[6]方法与考虑提出方法（或文献[2]方法）所需比特数目相同，取文献[6]方法的帧长为N′时，有M=32N′。

仿真中，取训练序列长度L=64，帧长度N=2L=128，M′=N′=48，M=32M′=1 536。特别地，仿真给出了正确同步概率的比较的一个特例。将在4.2和4.3节分别验证不同训练序列长度L和测量次数M对正确同步概率的影响，验证提出方法的普适性，仿真结果如图2所示。

图2给出了正确同步概率与信噪比的关系曲线，从图2可知：

图2 正确同步概率与信噪比的关系曲线

（1）当SNR≥25 dB时，提出方法与文献[2]方法和文献[6]方法均能达到近似为100%的正确概率。这说明在高SNR情况下（如该仿真所述的SNR≥25 dB），提出方法与文献[2]和文献[6]方法均能达到较高的同步概率。

（2）当SNR＜20 dB时，在相同正确同步概率情况下，提出方法所需的SNR低于文献[2]方法和文献[6]方法所需的SNR。如，取正确同步概率近似为100%时，提出方法所需的SNR约为0 dB，而文献[2]方法所需的SNR约为15 dB，文献[6]方法所需的SNR约为25 dB。这从另外一个方面表明，在相同SNR情况下，提出方法获得了更大的正确同步概率，即相对于文献[2]和文献[6]方法，提出方法改善了帧定时同步的正确同步概率。如，取SNR=5 dB时，提出方法的正确同步概率约为100%；而文献[2]方法的正确同步概率约为0.56，文献[6]方法的正确同步概率约为0.11。

4.1.2 所需比特数比较

在提出方法的正确同步概率不小于文献[2]和文献[6]方法的正确同步概率时，对比所需的比特数。取N=2L=128，仿真结果对比如图3所示。

图3 帧定时同步所需比特数与信噪比的关系曲线

图3 给出了帧定时同步所需比特数与信噪比的关系曲线，从图3可知：

（1）在提出方法的正确同步概率不小于文献[2]和文献[6]方法的正确同步概率时，对于相同SNR，提出方法的帧定时同步所需比特数均少于文献[2]和文献[6]方法的帧定时同步时所需的比特数。如SNR=5 dB时，提出方法帧定时同步所需比特数为512 bit；而文献[2]方法帧定时同步所需比特数为2 048 bit，文献[6]方法帧定时同步所需比特数为2 560 bit。

（2）相对于文献[2]和文献[6]方法，提出方法的量化过程仅需电平比较器，降低了ADC设计的难度。

为进一步验证提出方法相对于文献[2]和文献[6]方法的正确同步概率改善具有普适性，下面通过数值实验分别验证同步序列训练长度L和测量次数M对正确同步概率的影响。

4.2 训练序列的长度L对正确同步概率的影响

在采样所需的比特数相同的情况下，实验验证提出方法相对于文献[2]和文献[6]方法在不同训练序列长度L的情形下的有效性。取压缩采样与量化后的比特开销为M=2 048bit，帧长N=256，训练序列长度L分别考虑三种不同情形，即L=64，L=96和L=128。文献[2]和文献[6]方法仍考虑16 bit量化器，即 M′=N′=。仿真结果对比如图4所示。

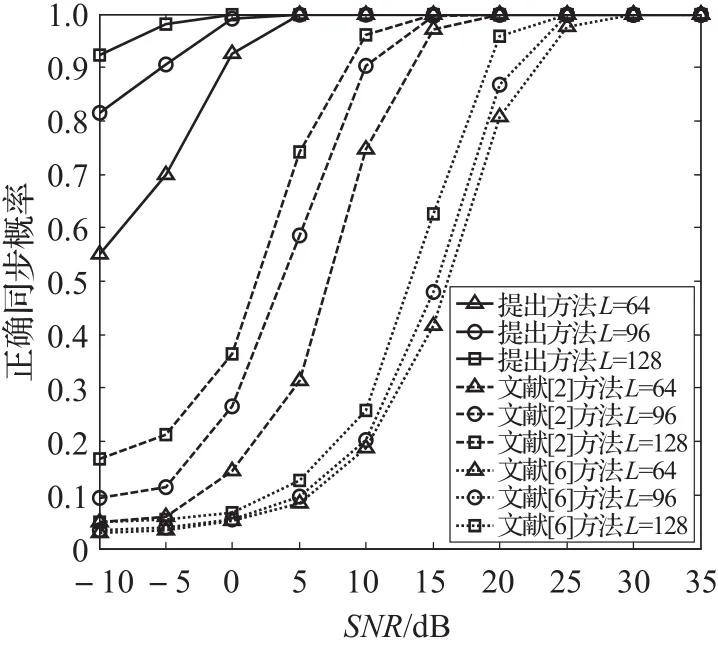
图4 同步序列长度L的改变对仿真结果的影响

图4 给出了不同训练序列长度L情况下正确同步概率与信噪比的关系曲线，从图4可知：

（1）随着L的增大，获得接近100%的正确同步概率所需的SNR随之减小。如为获得近似100%的正确同步概率，提出方法在 L=64时，需SNR＞5 dB；而当L=128时，提出方法仅需要SNR＞0 dB。类似的结果，也适用于文献[2]和文献[6]所述的帧定时同步方法。

（2）在相同SNR情况下，提出方法较文献[2]和文献[6]方法改善了正确同步概率（仿真给出的3种情形均有相同的结论）。如SNR=0 dB，L=96时，提出方法的正确同步概率约为100%；而文献[2]方法的正确同步概率约为0.27，文献[6]方法的正确同步概率约为0.05。

（3）根据（1）、（2）的分析，在相同的比特开销情况下，提出方法改善了帧定时同步的正确同步概率。同时，由于单比特量化，提出方法量化过程仅需要电平比较器，提出方法相对于文献[2]和文献[6]方法降低了ADC设计的难度。

4.3 测量次数M对正确同步概率的影响

保证比特开销相同，在帧长度N和训练序列长度L相同的情况下，实验验证提出方法相对于文献[2]方法在不同测量次数M的情形下的有效性。取帧长度N=256，训练序列长度L=64。取压缩采样与量化后的比特开销为Mbit，即提出方法的测量次数为M（测量次数M分别考虑三种不同的情形，M=1 024，M=2 048和 M=4 096）；文献[2]方法仍考虑16 bit量化器，为了便于区分，将文献[2]方法的测量次数表示为 M′，M′也考虑三种不同的情形，，仿真结果对比如

图5所示。

图5 测量次数M的改变对仿真结果的影响

图5 给出了不同测量次数M情况下正确同步概率与信噪比的关系曲线，从图5可知：

（1）随着M的增大，获得接近100%的正确同步概率所需的SNR随之减小。如为获得近似100%的正确同步概率，提出方法在M=1 024时，需SNR＞15 dB；而当M=4 096时，提出方法仅需要SNR＞10 dB。类似的结果，也适用于文献[2]所述的帧定时同步方法。

（2）在相同SNR情况下，提出方法较文献[2]方法改善了正确同步概率（仿真给出的三种情形均有相同的结论）。如SNR=10 dB时，提出方法在M=1 024时，正确同步概率约为0.99；而文献[2]方法在M′=32时，正确同步概率约为0.15。

（3）根据（1）、（2）的分析，在相同的比特开销情况下，提出方法改善了帧定时同步的正确同步概率；在相同正确同步概率情况下，提出方法所用比特数更少。同时，由于单比特量化，提出方法量化过程仅需要电平比较器，再次验证了提出方法相对于文献[2]方法降低了ADC设计的难度。

5 结论

本文提出一种基于单比特压缩感知的帧定时同步方法，以减少帧定时同步时所需的比特数，降低模拟数字转换器设计的难度。该方法首先对接收信号进行单比特的压缩采样，然后，对采样到的比特流进行重构得到帧定时同步的定时度量，最后，根据定时度量的最大幅度值索引找到帧的起始位置。研究结果表明，相对于文献[2]和文献[6]所述的帧定时同步方法，在相同正确同步概率情况下，提出方法所需比特数更少；在相同的比特开销时，提出方法相对于文献[2]和文献[6]可改善帧定时同步的正确同步概率。同时，提出方法的量化过程仅需要电平比较器，降低了模拟数字转换器设计难度。仿真结果验证了提出方法的有效性。