基于自适应小波阈值的心电信号降噪方法
王 磊,孙 玮,陈奕博,李 鹏,赵凌霄
中国科学院 苏州生物医学工程技术研究所,江苏 苏州 215163
1 引言
基于心电信号的判读能够辅助医生对多种心血管疾病进行及时准确的临床诊断,对于有效降低突发性心血管疾病引起的不可修复性损伤和死亡率具有重大意义。不论是人工判读还是基于各种机器学习方法的智能判读,都需要对心电信号中包含的P波、QRS波群、T波等波形进行特征提取和模式分类,而临床采集到的心电信号中往往含有大量的噪声信号影响了心电信号读取效果[1]。
更加准确有效地消除心电信号中的噪声干扰,提高临床心电信号的信噪比,一直是相关研究者的关注热点之一。针对心电信号的降噪问题比较常用的方法包括带通滤波器[2]、加权均值滤波器[3]、经验模式分解[4]、神经网络[5]、主成分分析[6]、独立成分分析[7]、自适应双阈值法[8]等,这些方法在心电信号滤波和降噪方面有各自优势和局限性。比如,自适应滤波器和基于神经网络的系统需要额外地参考信号和训练阶段,因此不适合于实时应用;主成分分析和独立成分分析的统计模型对信号的微小变化非常敏感,限制了其在临床的长期应用;经验模式分解对于固有模式函数的依赖过于严格,采用不适合的模式函数往往导致降噪性能的急剧下降。
小波变换作为应用数学领域的一个得到快速发展和应用验证的分支,已经成功应用于地震波分析、语音识别、图像分析等多个领域并取得了较好的效果。多尺度分析大大推动了小波变换的研究和应用,但是多尺度分析对于小波函数的选择、小波分解层次的设定以及阈值选取依赖性比较强,尤其是阈值选取,在小波变换的小波系数计算过程中直接影响结果的优劣,相关研究者针对小波阈值选取方法取得了一定研究成果[8-11]。
本文针对多尺度分析小波变换解决心电信号降噪问题提出了一种自适应的小波阈值计算和选取方法,该方法在启发式阈值优化方法基础上融入了小波分解层数和层级影响因子,通过动态调整每一层小波系数的阈值计算函数实现更加合理的信号分解与降噪处理。通过数值实验对所提出算法在心电信号降噪的效果方面进行检验,分析该方法在面向临床应用的心电信号降噪与分析领域应用的价值。
2 小波变换去除心电噪声原理
心电信号中往往包含各种不同类型的噪声而影响特征提取和分类。小波变换能够从时域和频域表征心电信号局部信息,通过时间窗和频域窗调整实现低频部分和高频部分的分别处理,从而达到心电信号降噪的目的。
2.1 心电信号噪声
临床采集获得的心电信号往往存在大量不同类型的噪声干扰,在进行心电特征提取和分类诊断之前需要去除这些噪声。归纳而言,心电信号噪声一般包含以下几类:
(1)基线漂移。心电信号采集过程中由于病人呼吸运动产生的干扰造成基线漂移,表现为心电信号呈现近似正弦曲线的波形。心电信号基线漂移的频率一般为0.05~2 Hz,振幅大约为15%。
(2)肌电干扰。人体肌肉的收缩会产生肌电信号,这种生物电信号加入到心电信号中将导致心电信号出现不规则快速波形变化。
(3)电极运动。贴覆于人体表面的电极如果由于人体运动产生电极移动甚至脱落,将导致心电信号波形出现较大的不规则变化。如果电极与人体连接中断,将明显看到50 Hz左右频率的工频干扰。
图1所示为加入不同类型噪声的心电信号对比图。原始心电信号从MIT-BIH心律失常数据库[12]获取,采用109号记录数据,基线漂移(BW)、肌电干扰(MA)、电极漂移(EM)噪声从MIT-BIH噪声压力测试集中获取。
2.2 小波变换
小波变换在母小波基础上进行缩放与平移,构成L2(ℝ)的一个标准正交基。连续小波变换(Continuous Wavelet Transform,CWT)的表达式如公式(1):
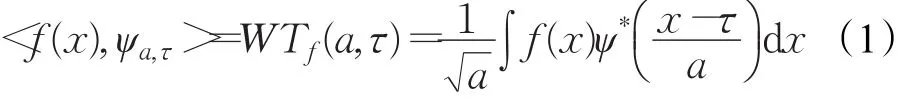
其中,f(x)表示信号函数,ψ(x)表示母函数,a(a>0)表示尺度因子,τ表示平移因子。
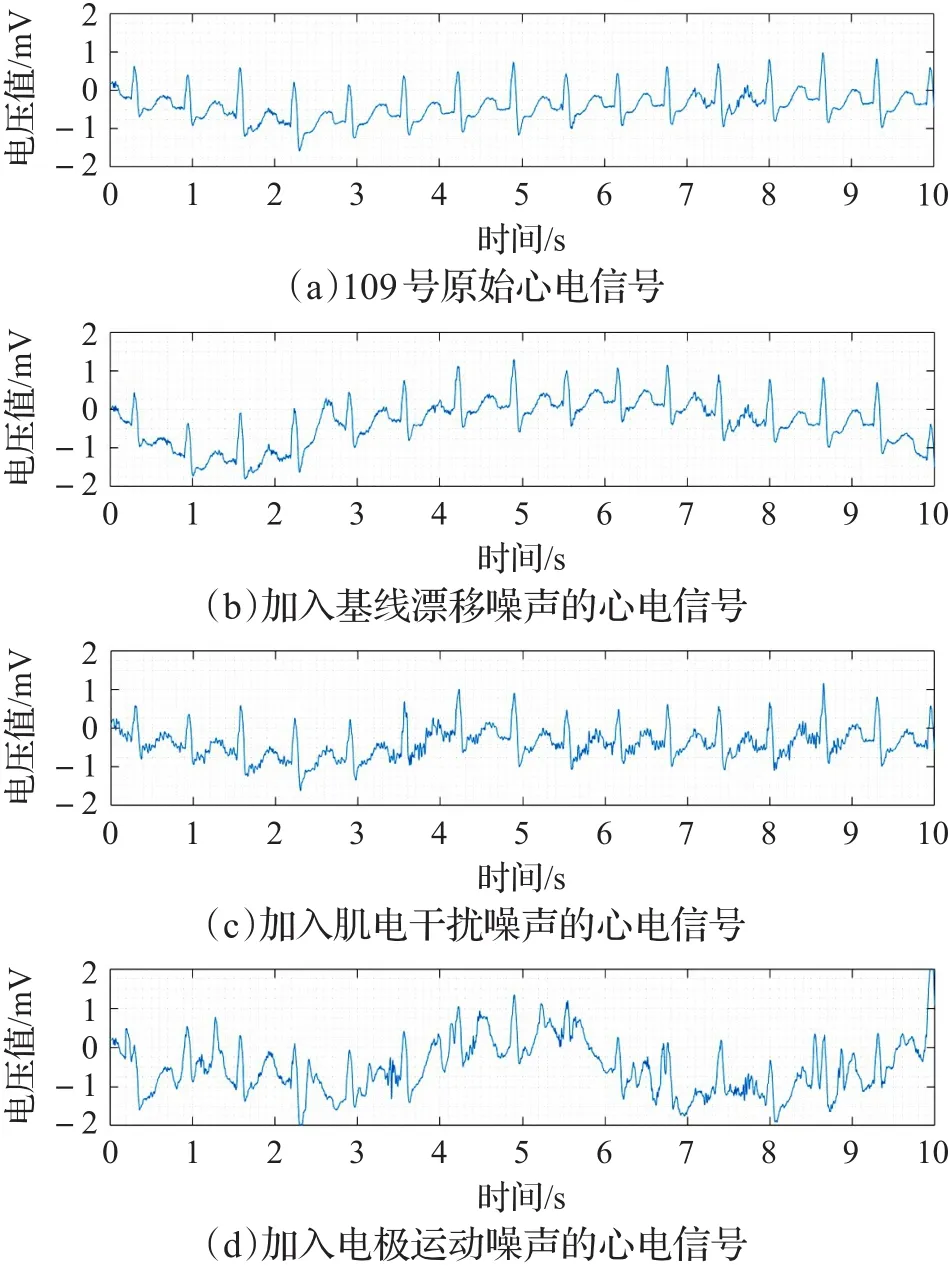
图1 含有不同噪声的心电信号
连续小波变换具有较强的相关性,在实际应用中往往采用离散小波变换(Discrete Wavelet Transform,DWT)。将连续小波变换的因子进行变换,尺度因子a=am0,平移因子τ=nτ0,如果选择 a0=2,τ0=1,则得到具有良好的时频局部化特性的离散小波变换母小波[10]:

转换之后的缩放和平移构成L2(ℝ)的一个正交基。离散小波变换使用一组二进制尺度因子从小波函数中提取信号的正交基。
采用离散小波变换可以将信号迭代式的分解,每次迭代从输入信号频率的中间值进行分解,并分别使用高通滤波器(HPF)和低通滤波器(LPF)进行信号过滤。如图2所示为三层小波变换信号分解过程。
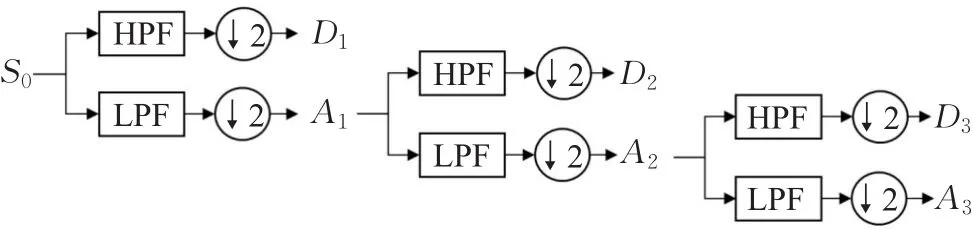
图2 三层小波变换信号分解过程
输入信号S0经过高通滤波器滤波和二元下采样得到高频子带信号D1,经过低通滤波器滤波和二元下采样得到低频子带信号A1;低频信号A1进行高/低频滤波和二元下采样进一步分解为高频子带信号D2和低频子带信号A2;A2进一步分解为高频子带信号D3和低频子带信号A3。输入信号经过小波变换分解可以表示为公式(3):

经过小波变换可以逐层细化信号低频部分特征,即实现多尺度分析,能够在心电信号降噪与特征提取中起到良好效果[13]。
2.3 小波阈值的选取
经过多尺度分辨小波分解后,能够在一定程度实现信号的小波系数幅值大于噪声的小波系数幅值,基于上述理论依据可以通过设定阈值将有效信号子空间保留,将噪声子空间去除,从而实现减少噪声的目的。小波阈值选取一般可以分为硬阈值和软阈值方法。
硬阈值方法将小波变换后大于设定阈值thr的信号子空间保留,小于设定阈值的噪声子空间小波系数置零,小波系数计算公式如式(4):

软阈值方法将大于设定阈值的信号子空间小波系数设为系数与阈值之差的阶跃函数Sgn结果,小于设定阈值的噪声子空间小波系数置零,小波系数计算公式如式(5):
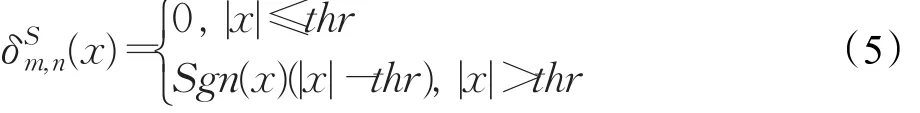
硬阈值方法得到的小波系数不可导,制约了其在信号重构的应用价值;软阈值方法得到的小波系数可导,因此在信号降噪领域应用较为广泛。
可以看出,阈值的选取对于小波变换应用效果具有关键作用。研究者针对阈值的选取进行了大量工作,比如针对包含大量高斯白噪声信号的通用阈值方法[14]、基于两个阈值优化选择的启发式确定方法[15]、双阈值方法等[8]。上述方法在图像、语音、生理信号降噪方面有各自优势,为小波变化的理论和应用研究拓展了思路。
3 基于自适应阈值的小波降噪方法
针对基于WBS远程心电监测的应用需求,提出一种自适应的小波阈值选取方法,用于解决临床心电信号包含大量噪声的信号降噪问题。首先分析小波函数的选择,然后提出自适应阈值的选取方法和降噪方法流程。
3.1 面向ECG的小波函数选择
Daubechies(dbN)小波系通过选取最小相位的平方根生成,滤波器将其最佳能量集中在其支撑点附近,具有不对称性。虽然在心电信号降噪研究领域有很多学者选用dbN小波作为小波基,但是受限于其对称性,在心电信号降噪效果方面有待进一步提高。
为了改进dbN小波的对称性缺陷,平方根的选择需要进行优化从而获得近似线性相位,保留最小支撑[-p+1,p]同时获得更大的对称性。在对称性方面改进的dbN小波称为Symlet小波,即“近似对称的紧支撑双正交小波”,在信号和图像处理方面获得了更好的频谱信息。另一方面,Symlet小波的缩放函数和小波函数形态比较接近心电信号波形,图3所示为Sym4、Sym6和Sym8小波基的缩放函数和小波函数形态[10]。
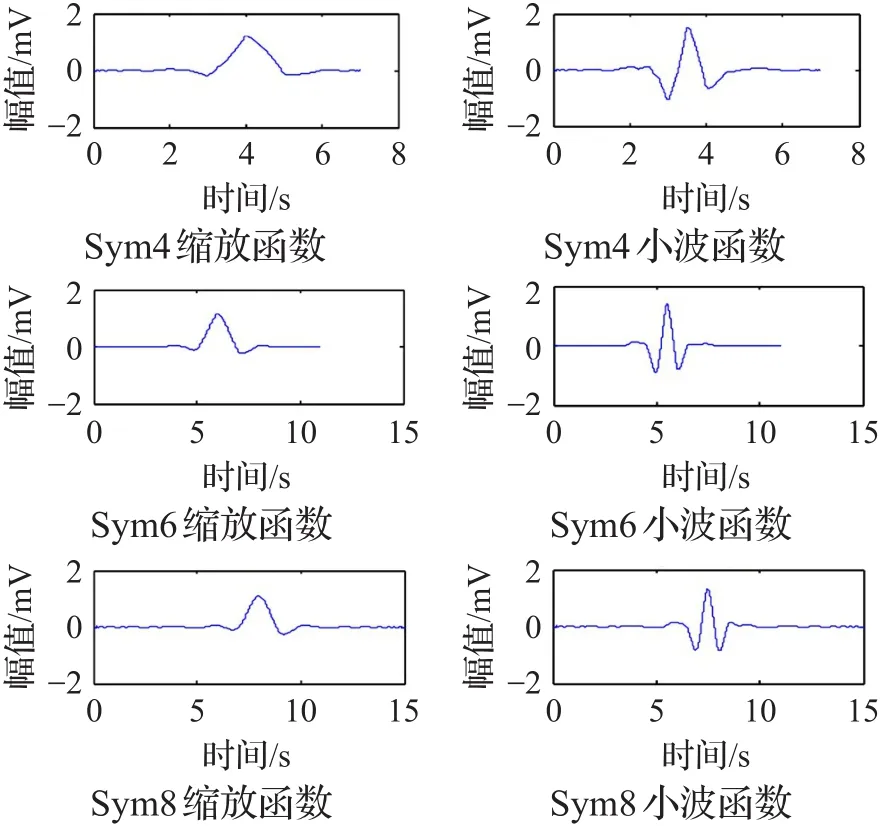
图3 Sym4、Sym6和Sym8小波缩放函数和小波函数形态
基于上述考虑,本文选择Symlet小波基对心电信号进行小波变换去噪处理。
3.2 自适应阈值的选取
固定阈值方法往往在某些信号测试样本上表现良好,而在某些测试样本性能急剧下降。采用优化选择的启发式阈值选取方法[15]能够在考虑噪声特点和小波分解过程中动态调整和选择阈值,往往能起到较好的实际效果。本文在启发式阈值方法基础上进行改进,提出一种自适应阈值选取方法。
基于小波变换的信号降噪在每层小波分解中都根据阈值进行高低频子带划分。如果采用全局一致的固定阈值则可能导致针对不同分解层次的信号子空间去除同样频带的噪声信号,造成原始信号偏离原来的形状。通过引入校正因子对阈值进行动态调整,可以解决针对不同频率子带设定更适合的阈值问题。一种基于校正因子的阈值选取方法如式(6)[16]:
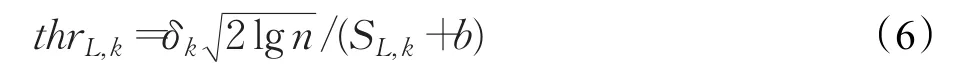
其中,SL,k为子带层次参数,用于体现不同分解层次的阈值调整,且有SL,k=2(L-k/L),L为小波分解的总共层数,k为当前的分解层数;δk=median|x|/0.674 5,b为调节因子。
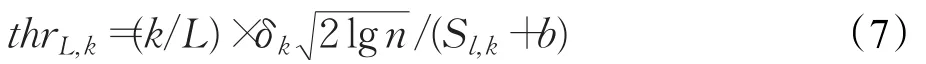
本文提出的根据小波分解层数的自适应阈值计算方法如式(7)所示:在阈值选取过程中通过收敛因子θ=k/L进一步调整阈值的计算结果,随着分解层数的增加而逐步减小阈值振幅,从而实现提高低频信号子带的分辨率。由于心电信号的有效部分大多分布于信号较平稳的低频部分,因此这种自适应阈值选取方法能够更有效地处理心电信号小波分解,提高心电信号降噪效果。
4 实验结果分析
为了检验本文提出的基于自适应小波阈值的心电信号降噪方法的有效性,针对MIT-BIH心律失常数据库中的部分心电信号数据进行测试,从小波函数基的性能比较、阈值选取方法降噪效果角度对降噪均方误差(MSE)、归一化降噪均方误差(NMSE)、信噪比提升(SNRimp)等测试指标进行对比分析。实验基于Matlab 9.0进行测试分析。
降噪的均方误差的计算公式如式(8)[17]:
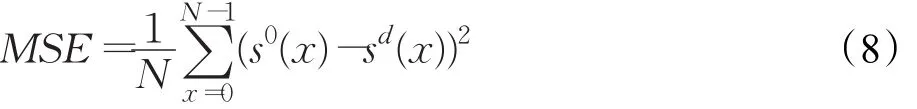
其中,s0(x)表示采集得到含有噪声的心电信号,sd(x)表示降噪处理之后的心电信号。
归一化降噪均方误差的计算公式如式(9):
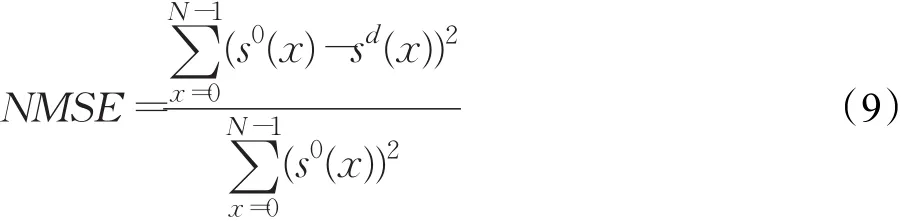
信噪比提升幅度的计算公式如式(10):
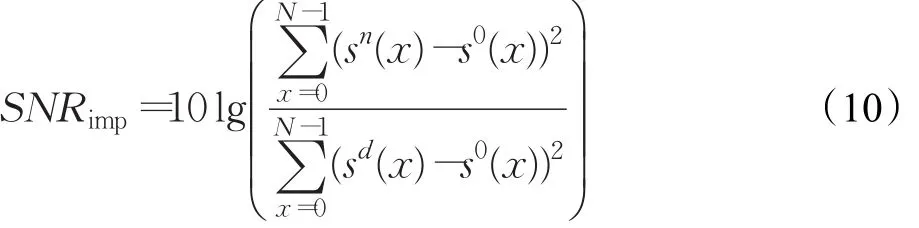
4.1 小波函数基的性能比较
本文选取Symlet小波作为小波基对心电信号进行降噪处理。为了对比分析Sym小波系中各个小波对于心电信号降噪效果,选取Sym1~Sym10共10个不同小波基进行对比分析,测试不同小波基对于心电信号中的基线漂移、肌电干扰和电极运动等不同类型噪声的信噪比提升幅度,结果如表1所示。
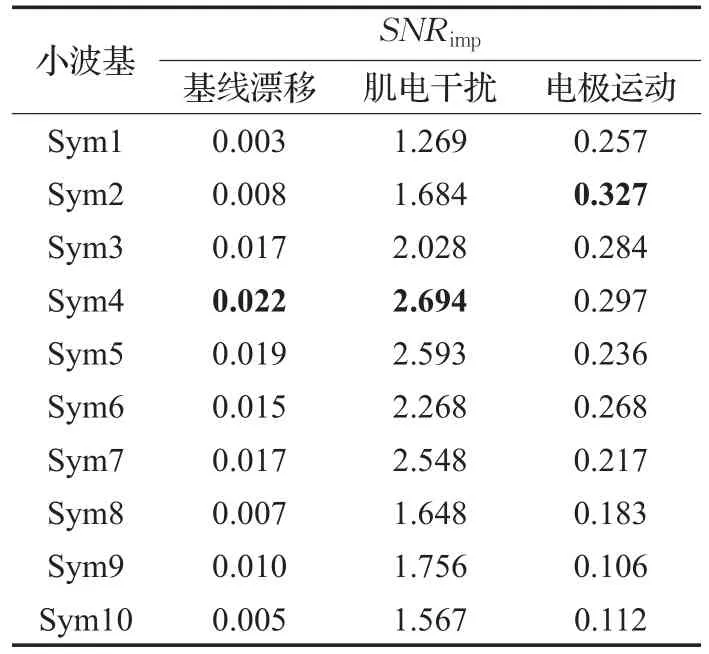
表1 不同Symlet小波基的降噪效果
从不同Symlet小波函数对于含有不同类型噪声的心电信号去燥效果来看,Sym4对于含有基线漂移和肌电干扰的心电信号降噪之后的信噪比提升较为明显,Sym2对于含有电极运动的心电信号的信噪比提升更明显。基于实验结果,本文选用Sym4作为小波函数对心电信号进行降噪处理。
4.2 小波分解层数的性能比较
影响小波变换运算效果的另一个重要因素是小波分解层数。选取Sym4作为小波基,分别采用1层~10层分解计算心电信号的信噪比提升幅度,实验结果如表2所示。
从小波分解层数对信噪比提升影响对比实验结果可以看出,在6~8层之间降噪结果比较好,分解层数较低或者较高往往降噪效果欠佳。对此结果进行分析,可以认为:如果小波分解层数较少,对于低频部分的多尺度分辨率不足,信噪比提高不多,信号降噪效果不明显,对于信号分辨率的提升效果未能满足要求;如果小波分解层数较多,在每层都对小波系数进行基于软阈值的处理后往往造成心电信号的信息大量丢失,降噪后的信噪比反而下降,同时由于分阶层数过多将加大运算负担,限制了临床应用价值。
基于上述实验结果和分析,在心电信号降噪处理过程中选用Sym4小波的6个分解层次。
4.3 阈值选取方法的降噪效果
本节将几种常用的小波阈值选取方法与本文提出的自适应阈值选取方法进行对比分析。选取MIT-BIH心律失常数据库101号记录加入包含基线漂移、肌电干扰和电极运动等三种混合噪声作为分析对象,分别应用阈值选取方法进行信号降噪处理,对比不同方法的降噪均方误差、归一化降噪均方误差、信噪比提升幅度。实验结果如表3所示。
从常用的小波阈值选取方法与本文方法对心电信号降噪效果对比实验结果可以看出,本文方法在归一化降噪均方误差和信噪比提升幅度方面具有较好的降噪表现,在降噪均方误差方面略逊于S-median方法。总体而言,基于优化选择和自适应的阈值选取方法在降噪效果上普遍优于固定阈值的降噪方法,但是由于阈值选取计算方法的调整可能影响其在不同测试信号上的表现,因此针对不同特征的心电信号设计更加适合的阈值计算方法显得更加关键。
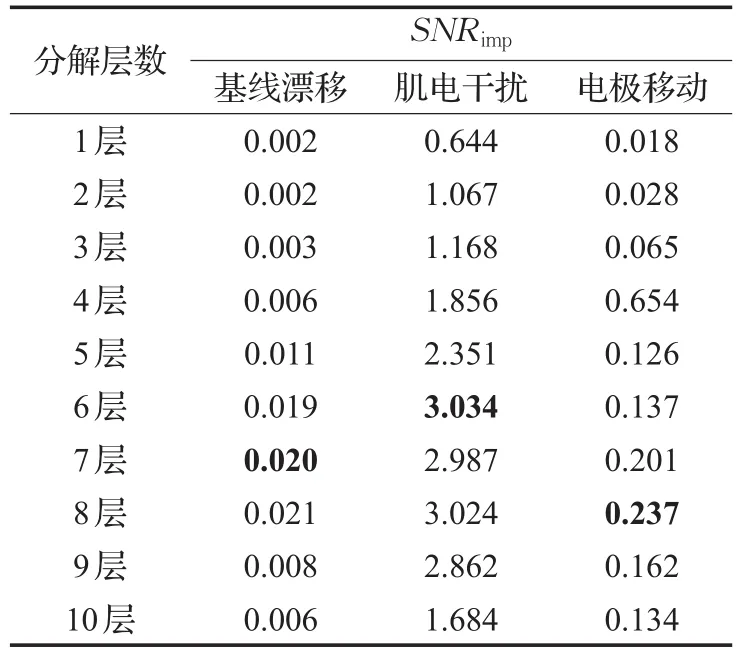
表2 不同小波分解层数的降噪效果

表3 不同阈值选取方法的降噪性能比较
5 结束语
心电信号降噪效果对于进一步的心电信号特征提取与模式分类起着重要作用,对于心电检测设备尤其是可穿戴式监护设备和远程医疗的推广应用具有基础性作用。本文针对基于小波多尺度分析的心电信号降噪问题提出了一种自适应的小波阈值计算和选取方法,该方法在优化选择方法基础上融入了小波分解层数和层级的影响因子,通过动态调整每一层小波系数的阈值实现更加合理的信号分解与降噪处理。实验结果表明所提出算法在心电信号降噪效果方面获得了较好的表现,对于小波分析在心电信号降噪与分析领域应用具有参考价值。
基于小波分解的信号分析方法对于小波函数、分阶层次和阈值选取的依赖性很强,结合实际应用场景设计更加适合的小波分析参数直接影响着信号降噪效果。另一方面,心电信号作为一种个体性差异较大,同时个体在不同时段也有突发变化的生理信号数据,有必要从大数据角度进一步研究考虑个体间差异和个体内不同时段差异性,并结合多模态数据融合技术探讨基于多种生理数据的临床辅助诊断方法。

