基于多种正则化的改进超分辨率重建算法

黄吉庆，王丽会，秦 进，程欣宇，张 健，李 智

贵州省智能医学影像分析与精准诊断重点实验室，贵州大学 计算机科学与技术学院，贵阳 550025

1 引言

由于成像设备分辨率的限制，外加噪声及运动等因素的影响，采集图像的分辨率通常较低，无法满足应用需求。为了解决这一问题，超分辨率（Super Resolution，SR）重建技术应运而生，即在不改变硬件条件的情况下，利用图像的先验知识恢复出低分辨率图像（Low Resolution，LR）的细节信息，进而重建出高分辨率图像（High Resolution，HR）。

目前，基于先验信息的超分辨率重建算法主要分为以下几类，即基于插值的算法、基于学习的算法和基于建模的算法[1-6]。其中基于插值的算法是利用邻近像素点的灰度值对待插像素点的灰度值进行估计。较好的算法有基于边缘导向的插值算法（Edge-Directed Interpolation，NEDI）和基于自学习特征的交替插值算法（Selflearned Characteristics Based Switched Image Interpolation，SLCSI）[7]。这两种方法在图像边缘和细节区域的重建效果有所提升，但仍无法完全克服图像插值算法的缺点，即基于局部信息的图像像素估计会引入图像的模糊，降低图像质量。

随着深度学习和人工智能的快速发展，基于学习的方法进行超分辨率图像重建逐渐成为主流。其思想是利用多组低分辨率和高分辨率图像，通过算法学习到低分辨率和高分辨率图像的对应关系。常用的超分辨率重建模型包括卷积神经网络模型[8]、残差神经网络模型[9]、深度卷积对抗生成网络模型[10]。但无论哪种学习模型，对低分辨率和高分辨率图像样本对的数目有很高的要求，并且训练的时间较长，不具有实时性和广泛应用性。

基于建模的方法是利用图像的降质模型对超分辨率图像重建提供约束，进而基于逆问题的求解方式获得超分辨率图像。在基于建模的方法中，通常加入正则项将病态问题转化为凸问题进行求解。目前常用的正则项包括L2范数、L1范数和LP范数正则项[11-20]。这些正则项通过对图像灰度梯度变化进行惩罚，进而实现降低平滑区域噪声并保持图像边缘和细节的效果。其中L2范数主要包括吉洪诺夫（Tikhonov Regularization，TR）和马尔科夫随机场（Markov Random Field，MRF）的正则项，这类正则项通过惩罚图像的高频部分，能够很好地降低图像的噪声，但会过度平滑图像的边缘和细节信息。全变分正则项（Total Variation，TV）是典型的L1范数正则项，这类正则项可以更好地保持边缘，但会在带有噪声的图像平滑区域产生阶梯效应。为了克服L1和L2范数正则项的缺点，研究学者们提出利用阈值算法优化L1和L2范数正则项，如Huber马尔科夫随机场（Huber-MRF，HMRF）和BTV（Bilateral TV，BTV）等正则项。这种改进算法通过设置图像灰度梯度的阈值，以区分图像边缘和平滑区域，对边缘使用L1范数正则项，而对平滑区域则使用L2范数正则项，但这种方法的重建效果对阈值的选择很敏感。为了解决这一问题，非局部变分正则项（Non-Local Total Variation，NLTV）先验被提出[21]，即在TV的基础上引入非局部相似度权重系数，可在一定程度上解决TV在平滑区域引起的块效应问题。NLTV中的权重系数通常符合高斯分布，因此，从本质上讲，NLTV的权重系数是一种非局部的均匀滤波器，仍会引起图像边缘模糊现象。

鉴于TV和NLTV正则先验互补的优势，本文提出一种结合TV和改进NLTV的多种正则先验的超分辨率重建算法。首先根据图像灰度梯度满足重尾分布的特点，将原有NLTV正则项的权重系数由高斯分布更改为更满足重尾分布的多种分布的结合形式，提出ANLTV（Amended NLTV）正则先验；然后利用ANLTV正则先验对超分辨率图像进行初始估计，最后采用TV正则项对超分辨率图像的初始估计进行去模糊操作，从而得到最终的超分辨率重建结果。

目前，求解带有TV类正则先验的优化问题的方法有很多种，如共轭梯度法（Conjugate Gradient Algorithm，CG），快速组合分裂算法（Fast Composite Splitting Algorithm，FCSA），交替方向乘子法（Alternating Direction Method of Multipliers，ADMM）以及分裂Bregman方法（Split Bregman Algorithm，SBA）等。其中CG方法利用目标函数的梯度信息，通过大量反复迭代，获得最优解，这种方法计算效率较低。FCSA是一种基于小波稀疏的凸优化的求解方法，求解效率相比CG方法有很大的提高，但这种方法求解时，会倾向于连续解，容易出现阶梯效应。ADMM和SBA方法是求解带有L1范数正则先验问题的有效方法，其中Bregman方法是ADMM方法的一种特殊形式，在参数设置合理时，能比ADMM方法更快的收敛[22]。因此，本文选择分裂Bregman算法对超分辨率图像进行求解。

2 基于多种正则化的改进超分辨率重建

2.1 图像降质模型

一般而言，低分辨率是由高分辨率图像经过模糊、下采样以及引入加性噪声等一系列降质过程获得的，因此按照降质模型，低分辨率与高分辨率图像之间的关系可以表示为：

其中y为低分辨率图像，D为下采样操作，h为点扩散函数，表示图像模糊过程，x为高分辨率图像，n为加性噪声，本文采用均值为0方差可调节的高斯噪声。

针对点扩散函数和下采样矩阵，本文采用了Antonio[9]提出的卷积下采样模型，这种模型同时完成了图像模糊和下采样过程，并且可以较快地进行降质和上采样，其表达式为：

式中D(x)代表图像下采样和模糊过程，S(y)代表上采样过程，具体的采样矩阵由Dx和Sx表示：

若高分辨率图像x的大小为2m×2m，则Dx的维度为m×2m，Sx的维度为2m×m。通过下采样操作D(x)，可以得到m×m大小的下采样图像y；通过上采样操作S(y)，可以得到y扩大两倍的上采样图像。

2.2 改进的超分辨率图像重建模型

根据图像的降质模型可知，为恢复出高分辨率图像，仅对低分辨率图像进行与降质模型对应的上采样操作即可。然而，由于降质模型的低秩性，使得这一逆过程的求解成为病态问题，无法获得最优解。为解决这个问题，需要在在求解过程中引入正则项，因此超分辨率图像的重建模型可表达为：

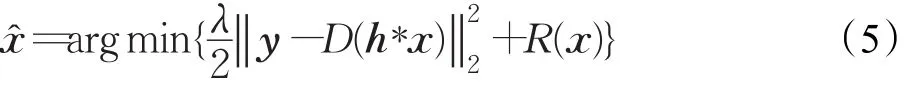
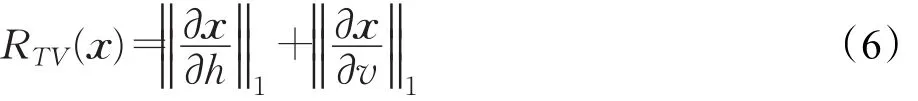
其中i表示图像x中的某一个像素点，Πi表示在图像x中以m2×m2大小窗口搜索时获得的与像素点i相似的所有像素点的集合，w(i,j)为权重函数，其定义为：

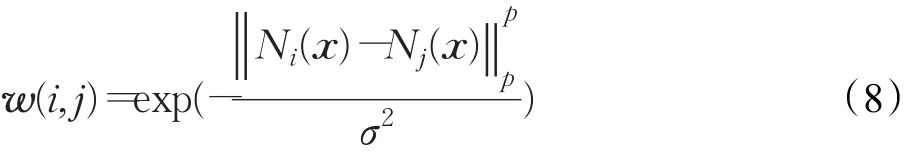
公式（8）中Ni(x)-Nj(x)分别表示图像 x在i和 j点处的某固定大小邻域上对应的灰度差值，邻域的窗口大小设置为m1×m1，p表示距离函数的范数，通常取值为2，代表像素点i和 j对应的邻域灰度的欧氏距离，σ为权重系数的调节参数。

在一幅图像中，图像灰度平滑区域占多数，因此针对平滑区域，相似块个数较多，公式（8）则相当于针对多个相似块实现一个高斯滤波，进而可以有效地去除图像平滑区域的噪声，解决TV正则先验引起的块效应问题。然而对于图像的边缘区域，由公式（8）可知，其权重系数很小并且快速衰减为0，如图1中的红色曲线所示，当灰度梯度的绝对值大于0.5时，权重系数趋近于0，若该灰度梯度出现的概率为0，则为0的高斯权重系数不会对结果有影响。然而自然图像的灰度梯度是符合重尾分布的，即较大灰度梯度出现的概率不为0，则此时若仍然使用高斯分布的权重系数，则会丢失图像的细节信息。因此，本文对NLTV正则项的权重系数进行修改，结合高斯分布，拉普拉斯分布及柯西分布提出ANLTV的权重系数，其表达式如下：

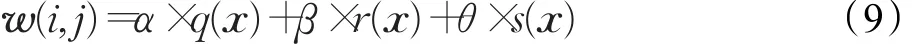
式中q(x)、r(x)和s(x)分别代表了高斯分布、柯西分布和拉普拉斯分布，α、β和θ分别为各种分布的加权系数，即：

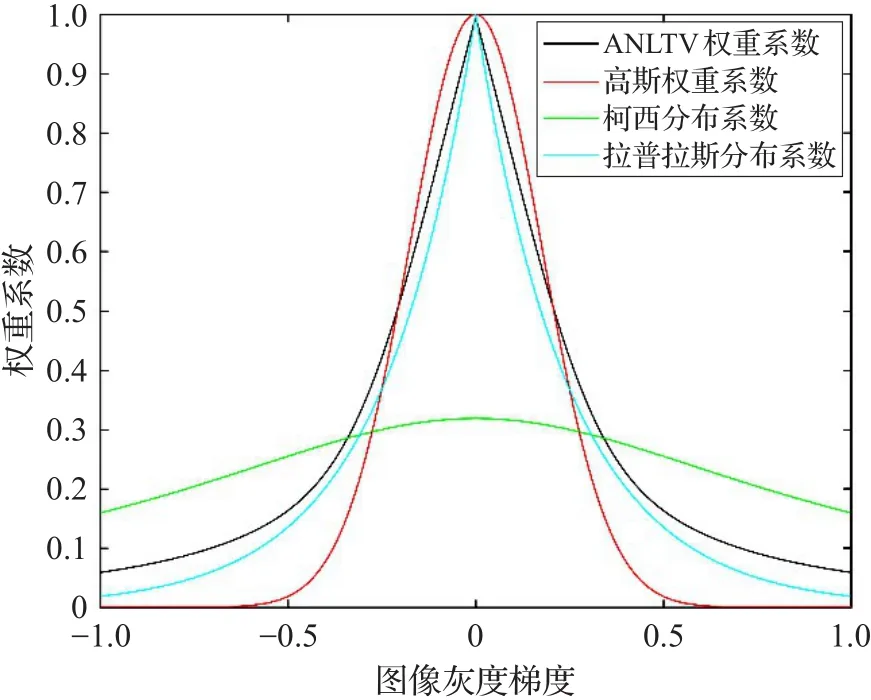
图1 权重系数与灰度梯度的关系示意图

图1 中的黑色曲线为ANLTV的权重系数，相比于高斯权重系数，可以看出，在图像的边缘区域，改进的权重系数尾部较厚重，更适合处理梯度满足重尾分布的图像。

虽然ANLTV的权重系数考虑了图像梯度变化的统计特性，能够保持图像的细节信息，但是不同相似块进行加权平均的过程中又不可避免地会引起图像边缘区域的模糊。为了解决这个问题，根据TV正则项在保持图像边缘方面的优势，在ANLTV正则化重建后，再利用TV对重建图像进行去模糊操作。综上所述，本文的超分辨率重建模型可以表示为：

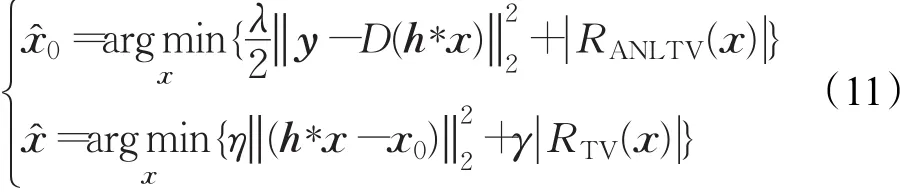
其中 ||·代表着一范数，RANLTV代表本文改进的NLTV正则项，RTV代表TV正则项，为基于ANLTV正则项初步重建的超分辨率图像，^为利用TV正则项对初始重建超分辨图像去模糊得到的结果。

为了求解公式（11）中的最小化问题，本文分别采用分裂Bregman方法对公式（11）中的两个优化问题进行迭代求解。

2.3 分裂Bregman算法求解

分裂Bregman方法是一种通过迭代，将正则项携带的先验信息传递到解之中的优化方法。它可以解决的问题形如：其中C是一个有界闭凸集，H(x)是可微凸函数，J(x)是凸正则项。

对于公式（9）所提出的超分辨率重建模型，满足分裂Bregman方法所能求解的问题。其中‖y - D(h*x)和‖(h * x-x0)对应可微凸函数H(x)，| RANLTV(x)|和|RTV(x)|是凸正则项，相当于J(x)。故公式（11）可采用分裂Bregman方法进行求解。以公式（11）的第一个公式（11）为例，对其求解过程进行详细的描述。

首先令d=RANLTV(x)，可得：

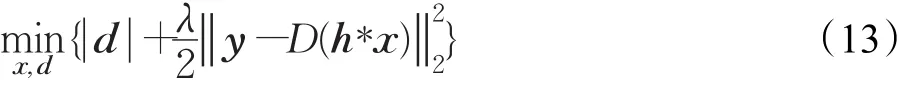
然后，根据拉格朗日乘子法，将这个带有约束条件的问题转化为非限制性问题，即：

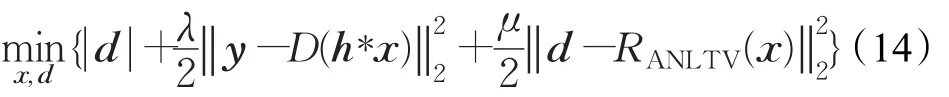
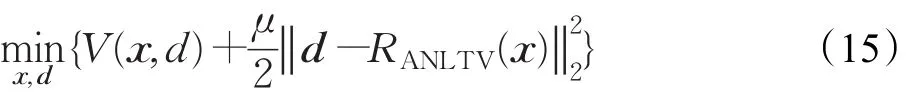
根据Bregman算法[20]的思想，公式（15）中V(x,d)可由Bregman距离(x,xk,d,dk)来代替，其定义为：

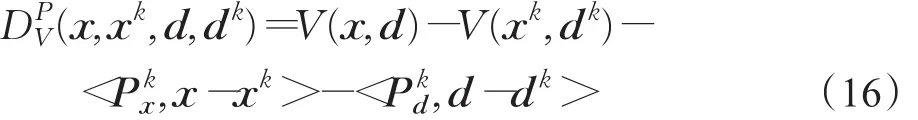
式中xk,dk为第k次迭代时获得的解，和分别表示函数V(x,d)在 xk,dk上的次梯度，即 (,)∈∂V(xk,dk)，＜·＞代表点乘操作。

将公式（16）代入到公式（15）可得第k+1次迭代获得的优化解为：

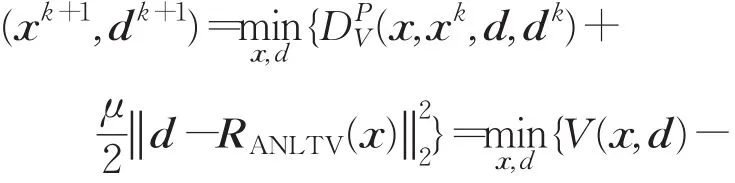
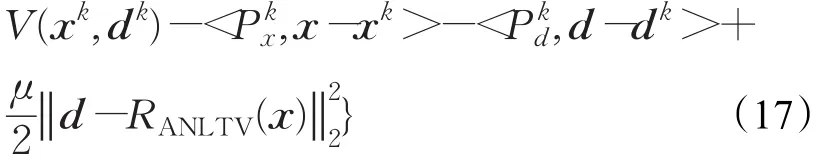
根据次梯度的定义，将公式（13）分别对x和d求导，可得到次梯度的迭代如下：

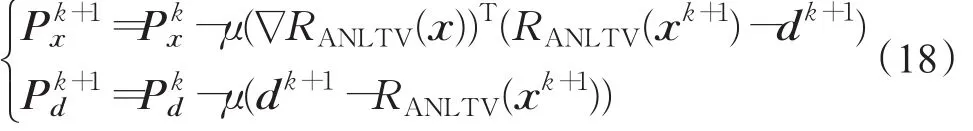
令bk+1=bk+(RANLTV(xk+1)-dk+1)，b0=0，迭代相加则得：

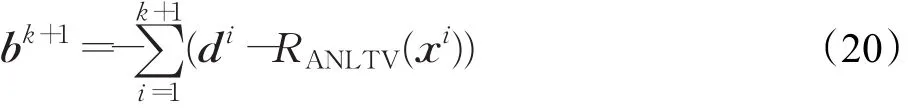
将公式（18）代入公式（17）中可得：

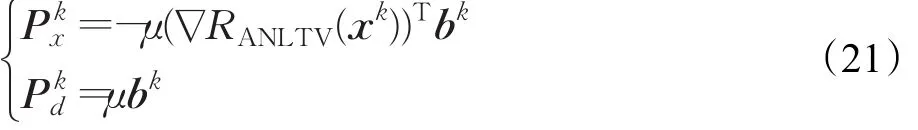
再将公式（21）代入到公式（17）中则有：

公式（20）中，C1和C2是常数项。为了加快公式（20）的迭代求解速度，利用分裂Bregman的思想，分别对x和d进行迭代求解，即：

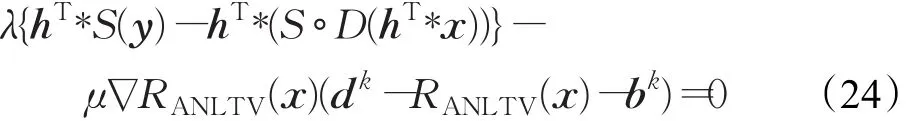
公式（21）对x进行求导等于零可得：其中S∘D表示对图像依次进行下采样S和上采样D操作。根据高斯赛德尔方法[23]对公式（22）进行求解，可得第k+1步迭代x的解：

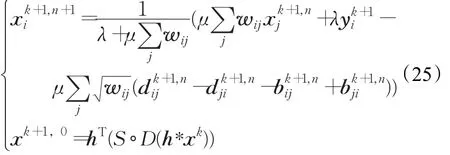
公式（21）对d进行求导等于零，并利用收缩算子可得第k+1步迭代d的解：

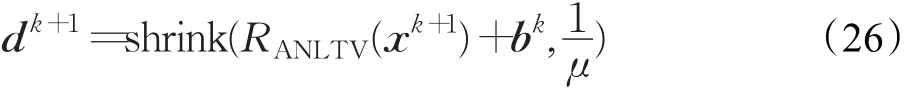
经过多次迭代，可以得到初步重建的高分辨率图像x^0。对初步获得的高分辨率图像x^0根据公式（11）的第二个公式进行去模糊处理，其求解过程与上述过程相同。

具体的算法求解流程图如下所示：

算法1 ANLTV超分辨率重建Bregman正则化

输入：低分辨率图像y，参数设置

输出：高分辨率图像x^0

初始化图像x0（使用双三次插值算法），初始化d0=b0=0

外层循环：

内层循环：

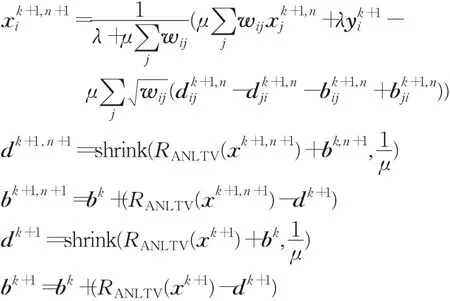
3 实验结果与分析

为了验证本文所提算法的性能，实验分别选取大小为512×512的Lena、Airfield、Baboon和Phantom图像为HR图像，利用2.1节阐述的图像降质模型，对图像进行模糊和下采样并添加加性噪声，得到对应的LR图像。再根据超分辨率图像重建的原理，分别利用基于ITV、ATV、NLTV以及本文改进的ANLTV+TV正则项的超分辨率重建算法进行重构。重建过程中不同方法所使用的参数如表1所示。

表1 超分辨率图像重建参数

为了提高不同算法重建图像的视觉对比效果，本文在几种图像中分别选择一个感兴趣区域，进行局部放大显示，如图2至图5所示，其中（a）显示了感兴趣区域，（b）为原始HR图像；（c）为下采样图像；（d）为ITV正则化重建结果；（e）为ATV正则化重建结果；（f）为NLTV正则化重建结果；（g）为本文所提出的ANLTV+TV正则化重建结果。

从Lena图（图2）和Airfield图（图3）的重建视觉效果上看，利用本文所提出的方法重建获得的超分辨率图像，在平滑区域噪声减少，并且在边缘区域对比度明显增加。这是由于ANLTV相比于原始的NLTV正则先验，满足重尾分布的权重系数没有屏蔽掉图像的细节信息，因此在边缘处理效果比NLTV要好很多。同时，经过ANLTV在图像平滑区域的均值滤波处理，可以很好地去除噪声的影响，进而再利用TV正则先验进行图像去模糊时，无块效应产生。

图2 Lena图像超分辨率重建结果

图3 Airfield图像超分辨率重建结果

图4 Baboon图像超分辨率重建结果

图5 Phantom图像超分辨率重建结果

图2 和图3是图像细节和图像平滑区域分布较均衡的图像，为了进一步验证本文算法，又分别对图像细节较多的Baboon图像和图像平滑区域较多的Phantom图像进行重建，其结果如图4和图5所示。从Baboon图像的重建结果可以看出，改进后算法很好地保证了边缘的对比度，展示出更多的细节信息。而针对平滑区域较多的Phantom图像，ATV和ITV算法在平滑区域仍存在着一些噪声；NLTV可以去除平滑区域的块效应，但是会模糊图像边缘；而ANLTV+TV在平滑区域几乎无噪声影响，并且边缘对比度较明显。

为了定量地分析4种不同正则项对于超分辨率图像重建效果的影响，本文采用峰值信噪比（Peak Signal-to-Noise Ratio，PSNR）、平均结构相似度（Structural Similarity Index，SSIM）和信噪比（Signal-to-Noise Ratio，SNR））3种评价指标对重建结果进行对比，如表2所示。

可以看出在两组图像中，本文所提出的方法在3种评价指标上都有一定的提升。针对Lena图像PSNR至少提高了6%，SNR至少提高了5%，SSIM提高了3%；对Airfield图像PSNR则至少提高10%，SNR提高了10%，SSIM提高了10%；对Baboon图像PSNR至少提高了3%，SNR提高了5%，SSIM提高了19%；而对于Phantom图像PSNR提高了8%，SNR提高了至少14%，SSIM至少提高了3%。可以看出针对不同特点的图像，各种评价指标的提升效果均不同，其原因可由图像灰度梯度的分布特点来解释，如图6所示。

从图6中可以看出，Baboon和Airfield图像的重尾分布最为明显，因此其在边缘的重建视觉效果最好，结构相似度提升较高。针对Lena图像，其灰度梯度分布尾部较高斯分布而言，不是很厚，但是在图像平滑区域，下降速度却比高斯分布快很多，说明在图像平滑区域相似性很大，所以处理加权均匀滤波时处理平滑区域效果很好，进而SNR得到很大的改善。尤其针对Phantom图像，其梯度分布曲线下降速度最快，所以利用本文方法，其SNR提升的最多，但由于尾部分布概率几乎为0，其SSIM并未提高很多。可以看出，利用本文所提方法，不管针对平滑图像，还是细节较多的图像，都能得到很好的重建效果。

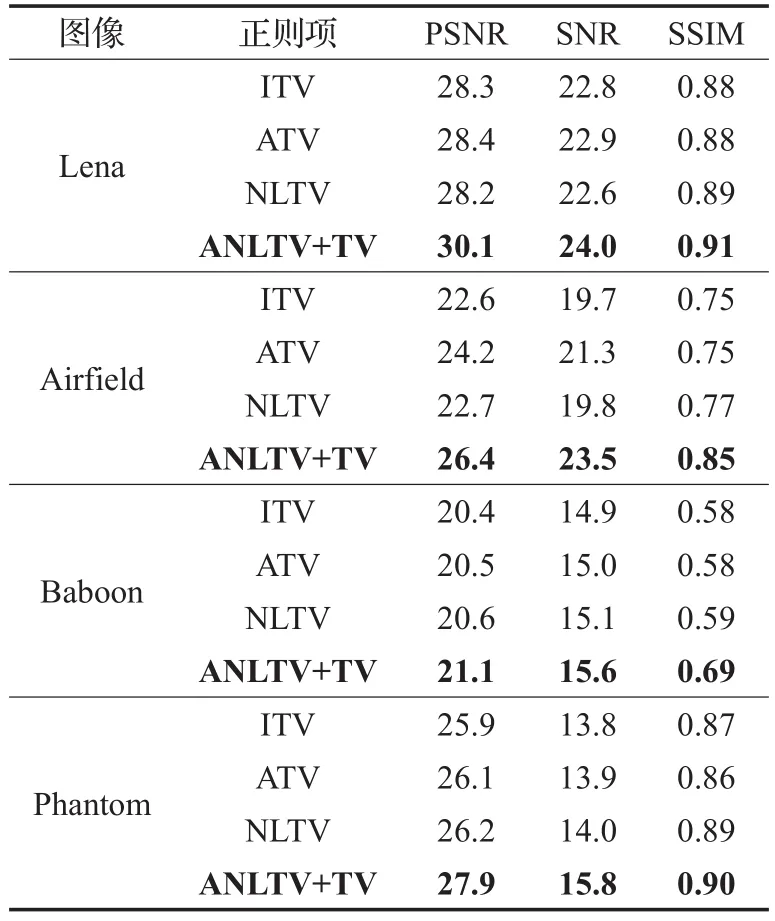
表2 4种不同正则项定量评价指标

图6 不同图像灰度梯度分布与高斯分布的区别

4 结论

本文针对超分辨率图像重建过程中，无法同时满足平滑噪声和保持图像边缘的问题，提出一种基于多个正则项的改进的超分辨率重建算法。首先利用自然图像灰度梯度满足重尾分布的特性，结合高斯、拉普拉斯和柯西分布改进了传统NLTV正则项的加权系数，进而提出一种新的ANLTV正则项，并利用该正则项对超分辨率图像进行初始重建。然后结合TV正则项在保持图像边缘方面的优势，利用TV正则项对初始重建图像进行去模糊操作，进而获得最终的超分辨率图像重建结果。实验结果表明，本文所提的超分辨率图像重建算法，相比于传统的基于TV和NLTV的超分辨率图像重建算法，无论针对平滑图像还是细节较多的图像，其峰值信噪比，信噪比以及结构相似性均有提升，在一定程度上解决了超分辨率重建过程中同时抑制噪声和保持边缘的矛盾。