基于分段Logistic映射的并行Hash函数构造算法

王 永，陈 燕，赵 毅

1.重庆邮电大学 计算机科学与技术学院，重庆 400065

2.重庆邮电大学 电子商务与现代物流重点实验室，重庆 400065

1 引言

Hash函数是信息安全领域中一种被广泛应用的基本技术。Hash函数以不同长度的消息作为输入，并产生固定长度Hash值，将其作为信息的摘要（或信息的指纹）。近年来，对常用的Hash函数如MD5[1]、SHA-1[2]等的攻击取得了突破性的进展。这也使得新的Hash函数的构造研究成为了当前的一个研究热点。混沌由于天然具有初值敏感性、伪随机性、难以预测等特性，受到研究者的青睐。当前，混沌成为构造密码算法的一种新的技术手段，被逐步广泛地应用于信息安全领域[3]。Liu等人利用具有鲁棒性的混沌映射构造了“一次一密”加密系统[4]，在图像加密中表现出良好的性能。将混沌映射与图像的位排列，以及与DNA编码结合，在图像加密中表现出很好的应用潜力[5-6]。此外，Wang等人将数学模型与混沌映射结合提出了新型的加密方法，展现出良好的加密特性[7]。基于混沌设计Hash函数是混沌密码中的一个研究分支。混沌Hash函数主要利用混沌迭代的不可逆性和初值敏感性来产生Hash值。与加密算法不同的是，Hash函数是利用签名来保证明文信息的完整性，更强调在将明文信息融入混沌迭代后，混沌轨道在相空间的均匀性。因此对混沌映射自身的特性的依赖性更好。文献[8-9]基于串行设计分别提出了时空混沌双扰动单向Hash函数和基于变参数循环移位的Hash函数，但是串行模式处理方式不能充分发挥多核CPU的并行处理优势。为此，研究者们提出了一些基于混沌系统的并行Hash函数设计方法[10-13]。从提高运行效率的角度出发，希望混沌映射的变换式相对简单，如文献[10]和[11]分别基于分段线性映射和Chebyshev映射，提出了并行Hash函数的构造算法。从提高算法安全性的角度出发，希望混沌映射的变化式相对复杂，从而保持混沌序列的高复杂性。文献[12]和[13]正是基于这样的思想分别基于洗牌交换网和动态混沌映射给出了相应的并行Hash函数构造算法。因此，怎样在混沌系统的复杂性和高效性之间找到合适的契合点，成为基于混沌系统设计Hash函数的一个重要研究点。此外，已有的研究表明，在并行处理消息的过程中，如果对消息的合并处理不当，构造出的Hash函数容易产生安全性漏洞。Guo等人[14]采用伪造攻击的方法，成功构建了文献[15]中的碰撞对。因此，如何防止伪造攻击成为了并行Hash函数设计中另外一个值得关注的问题。

针对上述问题，本文从兼顾效率与安全的角度出发，选取分段Logistic映射作为构造Hash函数的基础混沌映射。基于该映射提出了一种并行的混沌Hash函数构造算法。在该算法中，初始阶段利用混沌映射的迭代扩散明文消息块之间的相互影响，从而有效地防止了伪造攻击，保证了算法的安全性，为新型Hash函数的构造提供了参考。

2 分段Logistic映射

Logistic映射是在混沌密码算法设计中常用的一种混沌系统，具有结构简单运行效率高的特点，其表达式如下：

其中xj∈（0，1）为状态值，μ为控制参数。当前已有一些针对Logistic映射弱点的密码分析方法被提出[16]，因此提升Logistic映射的密码学特性变得非常有必要。

对Logistic映射进行分段处理后，可以得到分段Logistic映射（PLM）如下[17]：

式中N为分段数量，当控制参数μ∈（2，4]时该映射具有很好的混沌特性。与Logistic映射相比，PLM具有更好的密码学性质，如更大的Lyapunov指数，更好的遍历性。已有研究表明，PLM随着N的增大其Lyapunov指数也不断增大。此外，PLM同样具备一维混沌映射的高效性。这些特性使得PLM非常适合应用于混沌Hash算法的设计。

3 混沌Hash函数的构造

本文提出的基于混沌的并行Hash函数构造过程分三个部分：明文预处理、消息块处理、产生Hash值。明文预处理是将消息值经迭代后再分块以增强消息块间的扩散效果。消息块处理是对分块后的消息做并行处理，生成相应消息块的中间Hash值。产生Hash值是将每个消息块的中间Hash值经异或操作后获得最终Hash值。

3.1 明文预处理

（1）划分明文消息与补齐。设原始明文M的字节数为L，将M分割成128 Byte的消息块G1,G2,…,GR。若L不是128的整数倍，则对最后一个块进行填充。填充规则为：GR=*…*00…0length(M)，length(M)=Lmod255。将消息块依次存储在数组P中，每个元素P[i](i=1，2，…，128R）的长度为8 bit。如式（3）所示：

（2）增加明文字节间的关联。设置PLM中的N=64，x0=0.123 456 789，μ=4，将PLM迭代n0次以消除初始值的影响。然后，继续迭代产生状态值xs，将xs按式（4）转换为一个8 bit的整数 ks，并根据式（5）替换数组P中的每个元素值。

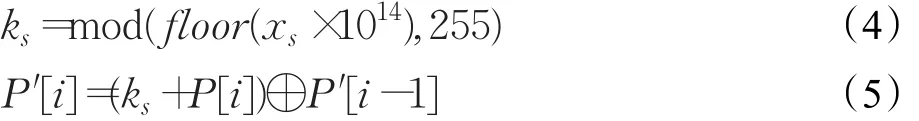
其中i=1,2,…,128R；s=1,2,…,128R。 P[i]是当前处理的明文值，P′[i]是P[i]替换后的值，且设置P′[0]=P[128R]。

（3）调整每个块中的首元素的值。将数组P′中的最后一个元素P′[128R]作为反馈值与每个消息块Gm（m=1，2，…，R）中的第一个元素 P′[128(m-1)+1]进行异或运算，如表达式（6）所示：

（4）迭代产生并行处理的初始参数。将首元素值调整后的消息块记为G′m，继续迭代PLM映射，迭代m次产生序列{gm}，分别将gm作为处理第m个消息块G′m(m=1,2,…,R)的初始参数。

3.2 消息块处理

预处理后的各明文消息块采用并行模式进行处理。对任一消息块G′m(m=1,2,…,R)，其处理流程图如图1所示。选取消息块G′m作为输入值，参数gm为初始参数，通过二轮迭代PLM映射，产生nbit的中间结果。参数qj∈（0，1），用于改变控制参数μ的值。yj表示一个二进制数，取值0或1。由序列{yj}构成的nbit值即为消息块G′m的中间结果。处理消息块的具体过程如下所示：

Let x0=gm,l=128,n=128

For j=1 to n

qj=P′[(m-1)l+j]255

μ=qj+xj-1+2

xj=PLM((qj+xj-1)2)

End

For j=n+1 to 2n

qj=P′[(m-1)l+2n-j+1]255

μ=qj+xj-1+2

xj=PLM((qj+xj-1)2)

If xj＞0&&xj＜=0.5

then yi=0

End If

If xj＞0.5&&xj＜=1

Then yi=1

End If

End

Return the middle hash value

H(m)=yn+1,yn+2,…,y2n

3.3 产生Hash值

消息块G′m经并行化处理后的输出值为H(m)，m=1,2,…,R。通过异或运算将所有消息块的输出合并到一起，即得到最后的Hash值H ，如式（7）所示：

图1 消息块处理流程图

4 混沌Hash函数的性能分析

4.1 Hash值分布

对一个安全可靠的Hash算法而言，由该算法产生的Hash值是均匀分布的。本文随意选取一段消息“Hash function is one of the major tools in cryptography，which is usually used for integrity protection in conjunction with message authentication and digital signature schemes.Chaotic dynamical systems possess the following main characteristics：sensitivity to tiny changes in initial conditions，unstable periodic orbits，desired diffusion and confusion properties，and oneway property.Due to these properties，chaotic systems have become a very good candidate for use in the field of cryptography.”统计该消息中ASCII码值的分布情况，以及由本文Hash算法所产生的Hash值（十六进制数）的分布情况，分别如图2和图3所示。

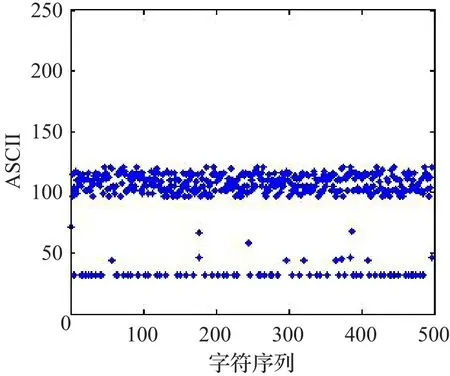
图2 明文消息ASCII码值分布图

从图中可以看出，明文消息的ASCII码值大多集中分布在100到130之间，其对应的十六进制的Hash值均匀地分布在整个区域，表明Hash值未暴露出任何与明文消息相关的统计信息。

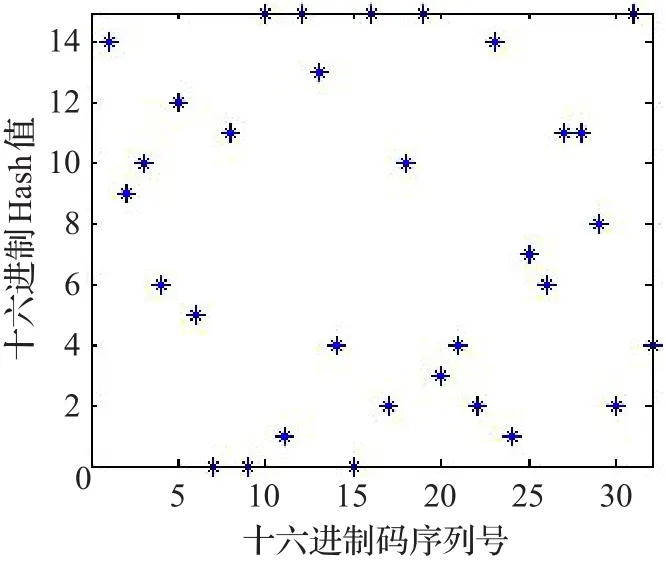
图3 十六进制Hash值分布图

4.2 敏感性分析

Hash算法应满足对明文消息的敏感依赖性，即明文信息发生微小变化，其对应的Hash值均能产生类似雪崩效应的输出结果。在本文的算法中，与敏感性相关的操作主要有两个方面：其一是在明文预处理中，利用PLM映射的迭代来增强字节之间的关联，再通过调整每个块中首元素的值，保证对明文任何位置的改变，都能传递到所有的块中；其二是在消息块处理部分，通过PLM状态值与消息块值之间的融合和迭代，来强化扩散的效果。由于PLM映射为混沌系统，天然具有初值的敏感依赖性，且通过分段处理增大了映射的Lyapunov指数，扩散性得到了增强。故本文算法能更好地保证Hash值对明文消息的敏感依赖。

本文在明文信息微小改变的条件下测试Hash值的变化情况，具体如下：

条件1同4.1节中的原始明文。

条件2将原始明文的首字母“H”改为“h”。

条件3 将原始明文的末尾“.”改为“，”。

条件4将原始明文的末尾加上1个空格。

条件5将原始明文中的单词“function”改为“functions”。

得到的Hash值（十六进制）如下，对应二进制序列如图4所示。

条件1 E9 A6 C5 0B 0F 1F D4 0F 2A F3 42 E1 76 BB 82 F4。

条件2 5D 0A BC 31 4A 54 84 A3 EF F0 22 4E E4 76 58 72（60）。

条件3 F1 FB B0 7C 1A F4 D3 46 55 05 63 CA 38 8D EF AC（68）。

条件4 30 43 4F 2A 75 1C 0C 96 5A 4F 9D C5 36 20 68 22（63）。

条件5 9C D9 99 F0 1E 63 18 34 41 CE 06 A3 52 01 57 97（69）。

图4 不同条件下Hash值比较

从实验结果可以看出，明文消息的细微改变都能引起Hash值发生巨大的变化，所以本文算法具有良好消息敏感性。

4.3 混乱与扩散分析

Hash函数的混乱与扩散特性主要是从统计的角度使得原始明文和Hash值之间的关系变得更复杂，且使明文的每一位均能影响Hash值。通常采用如下指标测量Hash函数的混乱与扩散性能：

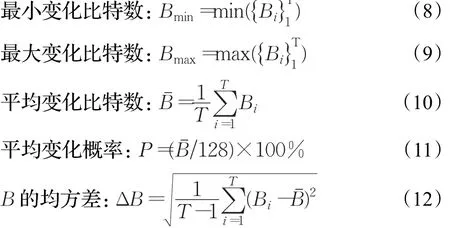
P的均方差：

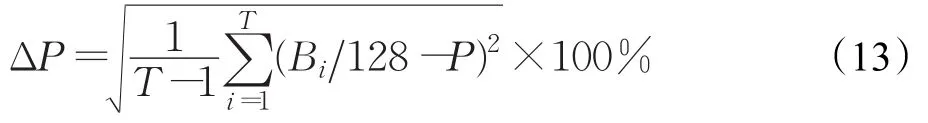
式中T为测试的总次数，Bi表示第i次测试时变化的比特数。

任意选取一段明文消息，产生其Hash值。然后，随机改变消息中某个比特的值，求得新的Hash值，比较两个Hash值的差异。分别重复上述操作256、512、1 024、2 048和10 000次，得到 Bˉ、P 、ΔB、ΔP 值如表1所示。

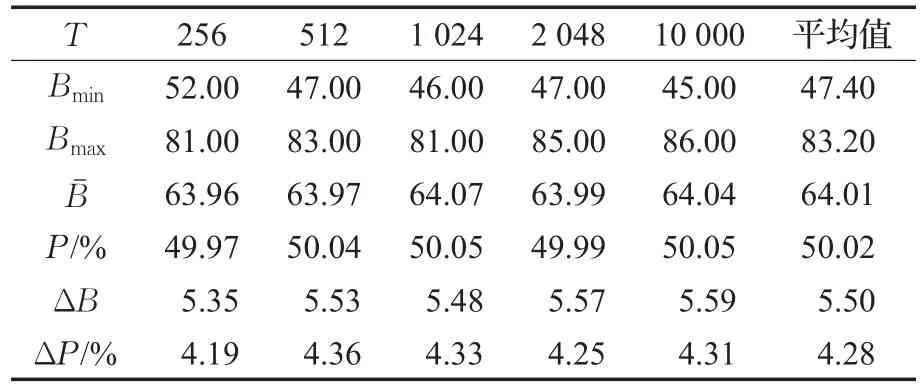
表1 实验结果统计

重复10 000次操作时得到的Hash值变化比特数的统计结果如图5和图6所示。实验结果表明，该算法的平均变化比特数Bˉ为64.01，每比特平均变化概率P为50.02%，接近理论值64和50%。ΔB与ΔP的值分别为5.50和4.28，都非常得小，这表明该算法的混乱和扩散性很稳定，能够抵抗统计攻击和差分攻击。

图5 Bˉ的分布图

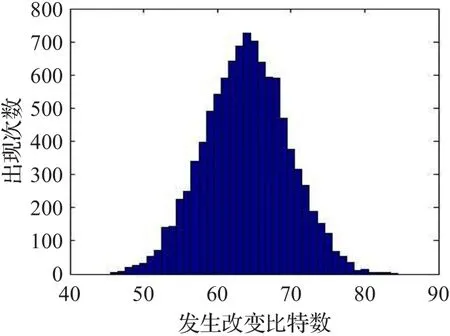
图6 变化比特数B的直方图

4.4 抗碰撞性分析

4.4.1 抗生日攻击分析

碰撞指随机给定两个不同的输入数据，而Hash值却相同，即发生了多对一映射。生日攻击与碰撞本质上是一样的，生日攻击指随机选取两个不同的明文消息计算各自的Hash值，比较它们的Hash值相同的概率。本文算法的Hash值长度为128 bit，且输出分布均匀，故生日攻击的复杂度为264，满足安全性的要求。

4.4.2 抗中间碰撞攻击分析

中间碰撞攻击的对象为Hash函数构造中的中间结果。在本文的算法中，每个消息块的输出是其中的一个中间结果。在中间结果的产生过程中，本文基于的是迭代PLM映射(N=64)的方式。就该映射而言，若已知其当前的状态值，推测其前一状态值，有128种可能性。在模块的处理过程中，总共迭代PLM的次数为256次。所以，在已知消息块输出结果的情况下，预测输入值计算量为128256，满足安全性的要求。

4.4.3 抗伪造攻击分析

伪造攻击指攻击者在已知几对明文和Hash值情况下，通过对这些消息进行组合和排列以实现碰撞。在文献[14]中，采用伪造攻击的方式，实现了对一些基于混沌的并行Hash函数的碰撞。这些基于混沌的Hash函数[15，18]之所以被破解，主要的原因为各明文块之间是相互独立的，没有考虑它们之间的关联与影响。在本文算法中，预处理阶段采取了两个方式来弥补：其一是通过链式结构，借助混沌映射的迭代实现各明文比特之间的关联与扩散；其二是通过最后一个字节的反馈来调整每个块的首字节值，从而强化扩散的效果。所以，本文算法能有效防止伪造攻击。

4.4.4 抗碰撞实验

混沌系统通常定义在实数域，对基于混沌映射的Hash函数，很难从数学上证明它的抗碰撞性。因此，本文根据文献[19]的方法定量分析该算法的抗碰撞性，通过式（14）计算T次实验中相邻Hash值的绝对差异度：

d=∑i=1

T

|t(ei)-t(e′i) （14）其中ei和e′i分别是原消息Hash值和修改消息后Hash值中的第i个ASCII码字符，函数t()将ASCII码字符转换为对应的十进制数值。

以4.3节中的10 000次实验数据作为样例，求得最大、最小绝对差异度如表2所示，以及在相同位置上有相同ASCII码值的个数分布如图7所示。本文算法的平均字符差异度为85.31，非常接近理想状态下[19]的理论值85.33，并且最大的相同字符数为2，说明该算法具有很好的抗碰撞性。

|602 1 365 85.31

表2 两个Hash值之间的绝对差异度d

相同ASCII码值的个数

图7 Hash值中有相同值的ASCII码字符的分布图

4.5 效率分析

在配置为Intel core i3 2120 3.30 GHz，8 GB RAM的计算机中，采用Visual C++6.0实现了本文算法。采用不同的线程数量，对长度不同的明文消息产生其对应的Hash值，测量算法的执行时间，结果如图8所示。计算结果表明，随着线程数量的增加，算法的执行效率明显提高。当线程为4个时，算法的处理速度为102 Mb/s。这表明该算法具有较高的执行效率，能够满足实际应用的需要。

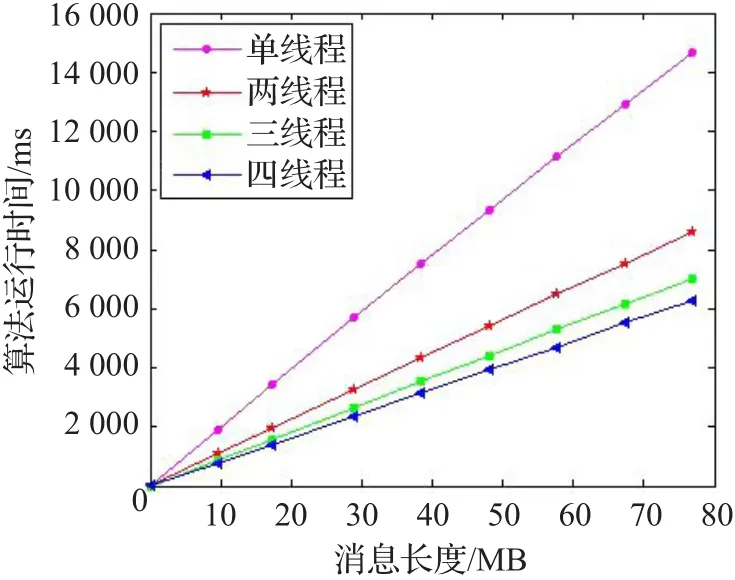
图8 算法的运行时间

4.6 对比分析

从当前国内外发表的文献中，选取类似的采用并行结构的Hash函数算法[12-13，19-21]与本文的算法进行比较。对比的结果如表3所示。

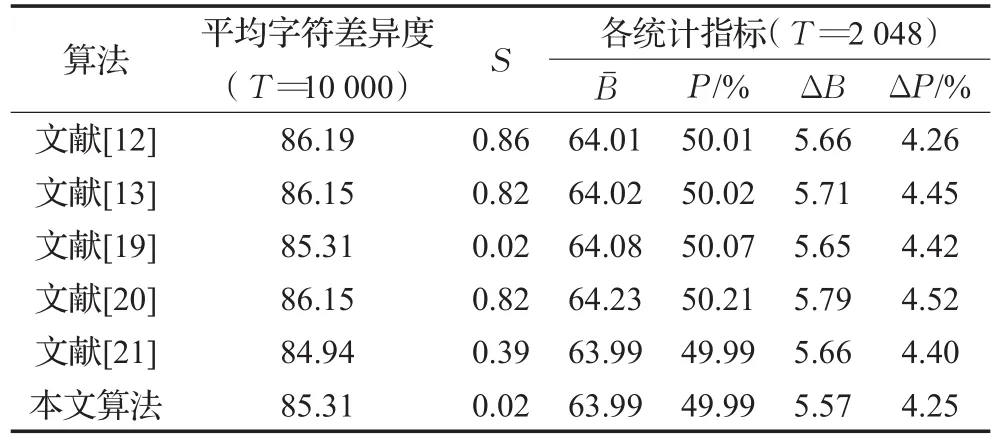
表3 随机测试T次的比较

从表3中可以看出，上述基于混沌的并行Hash函数均具有不错的统计性能和良好的抗碰撞性。与其他算法相比，本文算法的平均字符差异度为85.31，非常接近理论值85.33。在统计指标方面，本文算法的 Bˉ为63.99，P为49.99%与文献[21]中的结果相同，比其他算法更接近理论值64和50%。ΔB与ΔP的值分别为5.57和4.25，在所比较的算法中最小，表明该算法具有更好的混乱和扩散性。

5 结束语

本文利用分段Logistic映射运算速度快且具有良好密码学属性的特点，提出了一种新的并行混沌Hash函数构造算法。在明文预处理过程中，通过对每个消息值做链式变换操作以增强消息块间的扩散效果，从而提高该算法的抗碰撞性。在消息块的处理过程中采用了并行操作，消息块输出结果的合并为简单的异或运算，有效地减少了运算量，使算法在满足安全性的同时，具有很好的运行效率。理论分析与计算机仿真实验的结果表明，该算法能满足Hash函数的各项性能要求，具有良好的应用潜力。