地应力预测技术的研究现状与进展

印兴耀,马 妮,马正乾,宗兆云

(1.中国石油大学(华东)地球科学与技术学院,山东青岛266580;2.海洋国家实验室海洋矿产资源评价与探测技术功能实验室,山东青岛266071)

近年来,煤层气、页岩气、致密气和天然气水合物等非常规天然气资源越来越受到人们的重视,其中页岩气因为不仅具有较大的开发潜力和丰富的资源储量,而且具有分布范围广、开采寿命及生产周期较长等诸多优势,逐渐成为油气勘探开发的研究热点。目前,美国、加拿大、中国以及部分欧洲国家都开展了页岩气勘探、开发和生产等方面的研究工作,其中北美地区已实现页岩气商业开采,其页岩气勘探开发水平处于国际领先地位。

页岩本身的低孔低渗特征,决定了其只有经过大规模压裂改造才能获得商业产能,而地应力是影响压裂改造效果的关键因素,针对页岩地层的特征开展地应力研究是进行页岩储层开采的必要环节。从某种意义上讲,油气勘探开发过程中的油气运移和聚集、钻井过程中井壁的稳定、水平井设计、油层改造以及注水开发中井网的布置等工作都与地应力密切相关,如何有效且准确地预测页岩储层的地应力场对于油气勘探开发有着重要的意义。目前,专家学者们已经普遍认识到地应力在非常规页岩油气勘探开发中的作用,如何有效地进行地应力的研究及应用已成为地球物理领域的研究热点。为了使人们对地应力预测方法有更好的认识和了解,我们从地应力测量方法、地应力测井计算方法、地应力数值模拟方法及地应力地震预测方法四个方面介绍了地应力预测方法的研究现状,着重介绍了地应力的地震预测方法,探讨了如何利用地震数据估算地层的应力,最后对地应力地震预测技术的发展方向和前景进行了展望。

1 地应力测量方法

文献检索表明,国外地应力测量起步于20世纪初,Liearace利用应力解除法对胡佛坝下面的隧道进行了岩石应力测量,这是人类第一次直接对地应力进行测量的实例[1]。20世纪中期,HAST使用应力计对斯堪的纳维亚半岛进行了地应力测量,发现地层浅部垂直应力小于水平应力[2]。20世纪60年代以来,地应力测量方法开始多样化,除发展了扁千斤顶法、孔径变形法、光弹应力计法等平面应力测量方法外,还发展了三维地应力测量技术,通过单孔便可测得介质某一点的空间应力状态。1964年,FAIRHU-RST[3]提出了水力压裂地应力测量法,该方法是目前地壳深部地应力测量应用最普遍的方法。1968年,HAIMSON[4]从实验和理论两个方面对水力压裂地应力测量法做了全面分析。1972年,VON SCHONFELDT等[5]在明尼苏达州开展了真正意义上的水力压裂法地应力测量工作。20世纪80年代,瑞典发明了水下钻孔三向应变计,使用深度可达500m。我国地应力测量技术起步于20世纪四五十年代,1970年以后得到了快速发展,相继成功进行了水力压裂法、改进的深钻孔水下三向应变计等地应力测量,并成功研制了压磁应力解除法、凯瑟效应地应力测试等系统设备。近期,为加大深部资源勘探力度,提高灾害预报能力,我国启动了深部探测技术研究项目[6],这在一定程度上有助于我国地应力测量和监测网的建立。

到目前为止,人们共提出了数十种地应力测量方法,而且分类各异。本文依据测量得到的数据特点,从绝对应力测量和相对应力测量两个方面进行分类,并对其中一些比较常用的地应力测量方法进行阐述。绝对应力测量又可分为直接测量法和间接测量法,直接测量法包括水力压裂法、声发射法(AE法)、地质测绘法等,间接测量法包括套芯应力解除法、应力恢复法、X射线法、地质构造信息法、滞弹性应变恢复法等。

水力压裂法是在目的层段选取一段钻孔,利用一对橡胶封隔器对其进行密封,然后向密封空间中注入高压流体(一般采用比较经济的水),使密封段在流体压力的作用下出现裂缝,据此推测地层应力。该方法的优点是操作简单,适应性强,可对深层地应力进行测量。FAIRHURST[3]总结了水力压裂法的优势。HAIMSON等[7]指出了影响井壁裂缝产生的因素。经过多年的研究,水力压裂法在理论上获得了很大的发展。随后,RALEIGH[8]和HAIMSON等[9]也相继利用水力压裂法开展了地应力实际测量工作。从此水力压裂法逐渐被科学界所认同,在实际工程领域的应用越来越广。水力压裂法分为经典水力压裂法(HF法)和原生裂隙水力压裂法(HTPF法)。HF法是一种平面测量法,假设地层介质为均匀、各向同性、线性弹性、连续介质,同时要求钻孔方向与某一主应力方向相同。当假设不成立时,通过该方法测得的地层压力精度就会受到影响。HTPF法是HF法的发展,适用于原生裂隙较多的岩体[10],可以进行三维应力测量,而且不用考虑破坏准则以及钻孔方向等参数,但其耗时较长,影响计算精度的因素较多。

声发射法是依据Kaiser效应而提出的地应力测量方法。德国科学家Kaiser指出,在发生形变的多晶金属应力释放后重新加载时,若未达到历史最高应力水平,则物体内部很少发出弹性波;若加载的应力达到或超过了历史最高水平,则物体内部会发出大量的弹性波,并可从外部接收到。这一现象被称为Kaiser效应,从少量弹性波发出到大量弹性波发出的临界点被称为Kaiser点。通过实验获得地下岩石的各个方位的Kaiser点,便可得到地下岩石的原始应力状态[11]。

地质构造信息法是依据应力状态与地质构造密切的内在联系进行地应力预测的方法[12]。根据安德森理论,正断层、走滑断层、逆断层所对应的应力状态分别为σV>σH>σh,σH>σV>σh,σH>σh>σV,其中σh,σH依次为水平最小、最大主应力,σV为垂直主应力。同时,最大、最小应力方向与断层走向夹角的内在规律是可循的,所以基于这一规律可推测区域应力场的分布。HILL等[13]指出,利用地表倾斜仪测量地表形变分布并分析其特征,进而推测地下压裂裂缝的分布特征,可得到油区应力场的分布特征。NAKAMURA等[14]指出,可以通过调查火山口或侵入围岩的火山岩脉的分布形式等来推测最大水平主应力和最小水平主应力的方向。

应力恢复法由MAYER等[15]首次提出,先在钻孔孔壁开槽,将压力枕放入槽中,通过加压使槽子两侧测点的应力状态恢复至原始状态,即将测点距离恢复至开槽前的距离,此时的压力值便可看作原始应力值。其后,很多科学家对该方法进行了改进[16-18]。

套芯应力解除法,首先在岩心脱离母岩后发生形变恢复时测得应力解除而导致的弹性形变,然后通过实验测得岩层的弹性模量,最后利用胡克定律推知解除应力前地层的应力状态。该方法按照传感器的安装部位可以分为孔底应变测量法、孔壁应变测量法、孔壁切割测量法和孔径变形法[19-20]。

滞弹性应变恢复法(ASR法),主要方法原理如下:岩心离开母岩后,由于之前所受的地应力突然消失,岩心体积开始恢复,其中一部分为弹性形变,另外一部分为非弹性形变,而且之前各个方向所受的应力与形变恢复量成正比[21]。对岩心各个方向的应变恢复量进行测量,可获得主应变方向,进而推得主应力方向;根据岩性建立本构模型[22-24],便可获得主应力值。

相对应力测量包括钻孔应变测量、差应变曲线分析法(DSCA法)、差波速分析法等,限于篇幅,本文只对差应变曲线分析法作一介绍。差应变曲线分析法的基本过程是在实验室中对岩心定向施加围压,根据岩心各个方向上的应变量来估计地层应力状态[25-26]。REN等[27]通过实验进一步证明了DSCA法估测地应力的有效性和可靠性,并指出了这种方法的经济实用性。THIERCELIN等[28]对差应变曲线分析法做了进一步改进,并将其应用于实际地应力测量。该方法可以不用考虑岩心放置时间对预测结果的影响,与ASR法联合使用可得到更加理想的预测结果。

利用仪器测量得到的地应力比较准确,但数据量太小,成本很高,缺乏连续性,因此不适用于获得大范围的地应力数据。为了降低勘探开发成本,专家学者们研究了利用测井数据确定地层主应力方向并计算其大小的方法。由于测井资料具有测量深度较深、信息量大、数据相对连续等特点,基于测井资料计算地应力具有独特的优势。

2 地应力测井计算方法

据李志明等调研成果,20世纪70年代,斯伦贝谢测井公司开始研究利用测井资料解决地层力学相关问题(地应力是中间过程)的方法,并将其应用到石油勘探开发过程中解释地层坍塌压力、破裂压力以及油层出砂等问题[29]。20世纪80年代,我国各大油田开始应用测井资料计算地应力。20世纪90年代以来,随着国内外测井技术的飞速发展,测井资料越来越丰富,基于测井资料估算地应力的方法也越来越完善。本文从基于成像测井估算地应力、基于地层倾角测井判断地应力方位、基于声波测井估算地应力3个方面,介绍利用测井数据计算地应力的方法。

2.1 基于FMI或CBIL成像测井估算地应力

2.1.1 基于成像测井判断地应力方向

一个圆形井眼的受力情况如图1所示,σH,σh分别为最大水平主应力和最小水平主应力,p为钻井液对井壁的压力,R为井眼半径,θ为钻井液压力方向与最大水平主应力之间的夹角。对于距孔眼中心为r的地层任意点p1,其受力状况为[30]:

式中:σr,σθ,τθ依次为径向主应力、切向主应力及剪切应力。从(2)式可以发现,在最小主应力的方向上,切向正应力最大,此时易产生应力崩塌而形成椭圆井眼,这种现象被称为“井壁崩落”,应力崩塌导致的椭圆井眼长轴指示最小水平主应力方向。同时,在最大水平主应力方向上,切向正应力最小,当钻井液压力较大时,在该方向上的井眼表面会产生拉应力,如果拉应力超过岩石最大承受能力,则岩石破裂,产生诱导压裂缝,诱导压裂缝的走向指示最大水平主应力方向。此外,对于古构造应力未得到释放的地层,一旦钻开,则为构造应力释放创造了条件,有可能产生与之相关的一组裂缝——应力释放裂缝,这种裂缝的走向指示最大水平主应力方向。

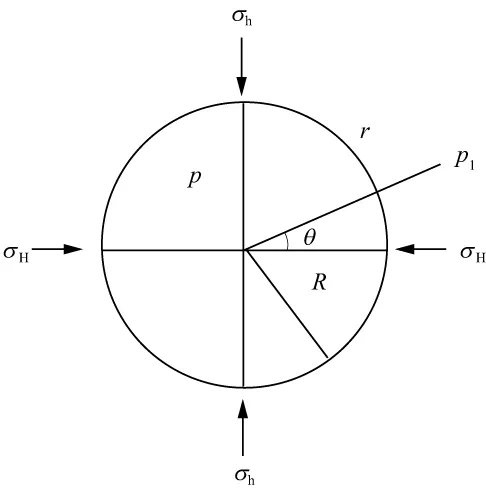
图1 井壁受力情况[30]

2.1.2 基于井眼崩落现象计算地应力大小

赵良孝等[31]、NIKOLAEVSKIY等[32]指出,利用双井径曲线、测井成像图求得井壁崩落的宽度和深度后,依据岩石力学性质,可求得最大、最小水平主应力如下:

σH=2×

(4)

σh=2×

(5)

其中,

式中:Δp=pm-pp,pm为钻井液压力,pp为孔隙压力,τ为岩石的粘聚力,f为岩石的内摩擦系数,C13和C24为不同方位的井径值,u为岩石的滑动摩擦系数,Dmax为最大井壁崩落深度,b为井壁崩落宽度,rw为井眼半径,θφ为井壁崩落与井壁交点的方位角。

最大井壁崩落深度Dmax和井壁崩落宽度b可以利用成像测井图中的暗色条带计算得到,井径值C13和C24可以利用双井径中的1-3井径曲线和2-4井径曲线获得。

(4)～(5)式基于井眼崩落已经稳定的状态而建立,刘之的等[33]据此给出井壁是否达到稳定状态的判别式:

(6)

式中:r1,r2分别为椭圆井眼的短半轴和长半轴;q是岩石自重;τs为岩石的抗剪强度。将成像测井得到的Dmax,b,rw以及计算得到的地应力代入(6)式,若该式成立,则井壁已达到稳定,此时基于井眼崩落现象计算的地应力值是可信的。

2.1.3 基于诱导压裂缝现象计算地应力大小

赵良孝等[31]只利用崩落宽度(不用崩落深度)计算地应力,然后依据井壁上的起始崩落边界点满足的剪切破裂条件建立如下公式:

(7)

式中:Δp=pm-pp,pm为钻井液压力,pp为孔隙压力;τs为岩石抗剪切强度;σH,σh分别为最大和最小水平主应力;θφ为井壁崩落与井壁交点的方位角。τs,θφ分别可由密度、声波测井数据和成像测井数据计算得到。

刘之的等[33]利用成像测井资料确定井壁诱导压裂平衡点,从而建立公式(8):

(8)

联立公式(7)～(8)便可求得最小和最大水平主应力。

2.2 基于声波测井估算地应力

2.2.1 基于多极子声波测井判断地应力方位

横波在因存在不平衡的地应力而产生各向异性的地层中传播时会发生分裂,沿最大应力方向传播速度比较快,即产生快横波。因此,可以在存在因地应力而导致各向异性的地层中用快横波的方位指示最大应力方向[34-38]。一般从多极子声波测井的波形数据中提取快慢横波速度和方位,然后根据快横波的方位确定最大应力方位。

研究表明,不仅不平衡的地应力可以导致地层各向异性,而且地层中发育的裂缝等因素也可以导致各向异性[39-46]。在裂缝地层中,横波的传播也会发生分裂,快横波沿裂缝走向传播,即快横波方位指示裂缝走向方位。所以,只有确定地层各向异性产生的原因,才能根据快慢横波方位正确地判断地应力方位。

刘之的等[33]给出了利用多极子声波测井确定地应力方位的步骤:

1) 从成像测井图中识别各种地质特征;

2) 判断产生地层各向异性的原因,譬如层理、裂缝、地应力等;

3) 根据多极子声波测井资料处理结果获得快横波方位;

4) 排除非地应力因素后,根据快横波方位判断最大主应力方向。

2.2.2 基于声波测井计算地应力大小

利用声波测井得到的纵波时差Δtp,横波时差Δts,加上密度测井得到的地层密度值ρ,可以获得岩石的动态力学参数[47-49]:动态泊松比μd,动态弹性模量Ed,剪切模量G,体积模量K,拉梅系数λ,岩石体积压缩系数Cb,骨架压缩系数Cma,Biot弹性系数α等。岩层中应力的形成、赋存条件更接近岩石静态测试环境,所以地应力大小的计算采用静态力学参数更加准确[50]。研究表明[50-51],可以先利用声波测井资料计算出岩体完整系数,然后求出折减系数,最后将动态力学参数转换为静态力学参数。基于静态力学参数便可求得连续的地应力大小。

1) 垂向地应力。根据密度测井资料可求得由岩石自重产生的垂向地应力[52]:

(9)

其中ρ(h)为随深度变化的地层密度,g为重力加速度,h为地层深度,H为目标计算点的深度。

2) 水平地应力[53-55]。计算水平地应力时,存在两种情况:第一种假设最大和最小水平地应力相等;第二种假设最大和最小水平地应力不相等,即两个水平方向上的应力不相等。第一种情况下建立了金尼克公式和马特威尔-凯利公式;第二种情况下建立了黄氏模型、弹簧模型等。

金尼克公式如下:

(10)

马特威尔-凯利公式如下:

(11)

式中:σv为垂向地应力,μ为岩石静态泊松比,pp为孔隙压力,σH和σh为最大和最小水平主应力。

黄氏模型:

其中,ω1和ω2分别反映两个水平方向上构造地应力的大小,不同地区对应不同值;α为Biot系数;σv为垂向地应力;σH和σh分别为最大和最小水平主应力;μ为岩石静态泊松比;pp为孔隙压力。该模型考虑了构造应力的影响,但是未充分考虑岩性对地层应力的影响,适用于构造平缓的地区。

弹簧模型:对于构造运动比较剧烈的地区,水平地应力的很大部分来源于地质构造运动产生的构造应力,不同性质的地层由于其抵抗外力的变形特点不同,因而其承受的构造应力也不相同。根据组合弹簧的构造运动模型推导的分层地应力计算模型为:

式中:E为静态杨氏模量;εh,εH分别为岩石在最小、最大水平应力方向的应变;σv为垂向地应力;σH,σh分别为最大、最小水平主应力;μ为岩石静态泊松比;pp为孔隙压力;α为Biot系数。该模型并未考虑倾斜地层,存在一定的局限性。

倾斜地层模型:大多数地层为倾斜地层,具有一定倾角和方位角。考虑地层倾角和上倾方位角的地应力计算模型为:

(16)

[σv-αpp)sinφsin(β-β0)+αpp]

(17)

式中:σv为垂向地应力;σH,σh分别为最大、最小水平主应力;μ为岩石静态泊松比;pp为孔隙压力;α为Biot系数;φ指地层倾角;A和B为构造应力系数。

分层地应力计算模式:葛洪魁等[56]针对水力压裂垂直缝和水平缝提出两组地应力计算经验公式。

当水力压裂为垂直缝时:

当水力压裂为水平缝时:

式中:E为静态杨氏模量;σv为垂向地应力;σH,σh分别为最大、最小水平主应力;μ为岩石静态泊松比;pp为孔隙压力;α为Biot系数;H为地层深度;Kh,KH分别为最小和最大水平主应力方向的构造系数;αT为线性膨胀系数;ΔT为地层温度的变化;Δσh,ΔσH分别为考虑地层剥蚀的最小和最大水平附加量。该模型考虑的因素比较全面,更加符合地应力分布规律,而且公式中的参数比较容易获取,因此适用范围更广。

2.3 基于地层倾角测井判断地应力方位

根据地层倾角测井提供的井径曲线和极板方位角曲线,可以判断井壁崩落方位,从而获得地应力方向。

地层倾角测井可以获得不同方位的井径曲线,井斜方位角AZIM,一号极板相对方位角RB,一号极板方位角PIAZ以及井斜角DEVI。以六臂地层倾角测井为例,可测得夹角为60°的1-4极板井径曲线C14,2-5极板井径曲线C25,3-6极板井径曲线C36。测井仪器在测量过程中会随着提升而不断旋转,当测遇崩落井段时,一对测臂将嵌入椭圆井眼长轴方向的槽内,使仪器不再随着提升而旋转,此时测得的大井径即对应着椭圆井眼的长轴。如果井眼崩落是由于地应力不均衡引起的,则椭圆长轴方向对应最小水平主应力方向,即:

当C14最大时,θAZIM(σh)=θPIAZ=θAZIM+arctan(tanθRB/cosθDEVI);

当C25最大时,θAZIM(σh)=θPIAZ±60=θAZIM+arctan(tanθRB/cosθDEVI)±60;

当C36最大时,θAZIM(σh)=θPIAZ±120=θAZIM+arctan(tanθRB/cosθDEVI)±120。

其中,θAZIM(σh)为最小水平主应力方向,θPIAZ为一号极板方位角,θAZIM为井斜方位角,θRB为一号极板相对方位角,θDEVI为井斜角。

引起井壁崩落的原因不仅仅只是地应力不均衡,冲刷崩落、裂缝崩落等都可以形成椭圆井眼[57]。为排除非应力因素导致的地层崩落,赵永强[58]提出了识别应力型椭圆井眼的方法:①井径差较大,即一条井径曲线值显然大于另外两条井径曲线值;②井眼崩落段具有一定长度,长轴方位较为固定;③测遇井眼崩落段,测井仪器基本不再随着提升而旋转。

因此,基于地层倾角测井资料确定地应力方位时,首先应该根据井径曲线和极板方位角的特征确定井壁崩落段,然后根据井径曲线的相对大小和极板方位角判断最小水平主应力方位,最后统计并确定最小水平主应力的优势方位。

目前,已有很多学者将基于测井技术计算地应力的方法应用到实际资料处理中,并取得了很好的效果[59-63],证明了基于测井技术计算地应力的实用性。

3 地应力数值模拟方法

随着计算机技术的迅猛发展,利用数值模拟方法对地下介质地应力分布进行预测成为了可能。BEAUMONT等[64]建立了一套比较完整的数值模拟系统,通过对地质构造成因进行分析,选择适用的边界条件,模拟应力场分布规律。陈书平等[65]通过分析某地区的构造运动演化过程,利用有限元方法模拟每个时期的应力分布规律,总结了应力场与油气分布的关系。杨柯等[66]针对应力函数法存在的问题提出了应变函数法,利用该方法对地下洞室群周围的地应力分布情况进行了分析。曾联波等[67]基于有限元法定性讨论了地应力对油气运移、聚集的影响。PARSONS[68]基于GPS数据分析了目标区的边界约束条件,通过建立有限元模型,对该区的构造应力场特征进行了分析。ECKERT[69]利用有限元软件ABAQUS模拟了美国某工区的三维地应力场,并逐步精细分析了该工区地应力场的特征。MATSUKI等[70]提出了利用接触单元模拟断层的有限元方法,分析了含断层区块的地应力分布情况。刘雄[71]基于Petrel地质模型,利用弹性力学和有限元法开发了地应力数值模拟软件TSM。李亚旭[72]实现了低孔渗气藏三维现今地应力数值计算。本文将从边界位移调整法、边界载荷调整法、位移反分析法、应力函数法和位移函数法等五个方面对地应力的数值模拟方法进行阐述。

3.1 边界位移调整法

郭怀志等[73]提出了通过不断调整边界位移值,使实测点处数值模拟值与实测值相吻合的方法。朱伯芳[74]对该方法进行了改进,指出在设计阶段不用反演地应力的垂直分量,直接采用密度在深度域的积分值代替,这样可以减少回归变量,提高回归精度。具体方法是:首先依据地质调查结果建立研究区域的地质力学模型,然后基于最小二乘原理,运用多元回归分析方法,通过不断调整边界的位移值,使研究区域内地应力实测值与数值模拟值实现最佳拟合,从而获得研究区域的应力分布。应用该方法进行地应力场分析主要受到五个因素的影响[75]:几何模型的形状及大小、区域框架、边界条件的选择、地质力学模型的建立、模拟值与实测值的最佳拟合判断条件。其中几何模型和力学模型的建立基于地质调查和其它先验信息,相对比较简单,而其它三个因素较复杂。区域构造框架的选择需要考虑岩层合并问题和搓动、叠加的构造带、力学结构面的选择问题;边界条件的确定需要考虑其它方法获得的应变、地应力先验信息。

3.2 边界载荷调整法

薛玺成等[76]提出边界载荷调整法,该方法与边界位移调整法相似,通过调整边界载荷的作用方式和大小,使研究区域内地应力实测值与数值模拟值实现最佳拟合,从而获得研究区域的应力分布。

边界位移调整法和边界载荷调整法对边界条件的调整均无规律可循,工作量非常大,在考虑非均匀性等复杂地质情况后,工作量将会更大,而且所假设的应力或位移需要满足变形协调和平衡条件,使问题变得更加复杂。因此,这两种方法比较适用于介质和地应力分布比较简单的情况。

3.3 位移反分析法

位移反分析法主要是利用位移信息反推地下介质的初始地应力或边界载荷[77]。根据地下介质的性质和力学状态的不同,选用不同的应力应变关系进行弹性位移反分析、粘弹性位移反分析、弹塑性位移反分析或黏弹塑性位移反分析,从而获得弹性参数、粘弹性参数、弹塑性参数或黏弹塑性参数。

根据实现过程的差异,数值反分析可以分为逆解法和直接法[78]。逆解法是利用已知的位移信息,基于正分析方程推导得到的逆方程计算得到初始地应力场的方法,仅适用于容易获得逆方程的线性弹性介质;直接法是基于最优化正分析方程建立的目标函数得到地应力分布,其适用范围比较广。在计算工区缺乏地应力资料等情况下,位移反分析法比较实用。

3.4 应力函数法和位移函数法

应力函数法/位移函数法先利用平衡方程、本构方程和实测点的应力/位移测量值、坐标值和应力/位移边界条件构建回归方程,然后利用最小二乘原理确定回归系数,通过回归分析得到应力/应变函数,最后利用有限元法校正回归分析的结果,对回归结果进行改进,得到地下应力场的分布。

张有天等[79]建议使用四次多项式应力函数对地应力分布进行预测,同时推导了三维和二维应力函数,并以实例对其进行了说明。杨柯[66]通过回归分析获得应变函数,并将其应用于地下洞室群周围的应力预测。

应力/位移函数法操作简单,但复杂情况下难以获得较好的结果。其中应力函数法在用于有限元计算时无法直接施加消除模型刚体位移的约束条件,只能通过迭代来消除刚体位移;位移函数法能很好地解决这个问题[66]。

数值模拟地应力分布多以实测数据为基础,同时考虑地形、地质特点,建立模型进行反演回算、模拟。除了以上五种方法外,还有很多其它方法,譬如,李龙林等[80]将灰色系统方法引入有限元模型回归分析中预测地应力分布;石敦敦等[81]研究了人工神经网络结合遗传算法反演岩体初始地应力的方法;GIODA[82]提出了同时确定初始应力场和地层特性参数的优化反演理论。每种方法都有相应的适用条件,在实际资料处理中,应该针对实际情况选用合适的方法。

4 地应力地震预测方法

利用地震数据估算地应力是正在发展的一种地应力预测方法,该方法能够得到某个区域连续的地应力剖面,对地下介质进行全面的地应力预测。

DILLEN[83]建立了反射系数与应力间的关系,为地震数据反演应力分布提供了可能;SARKAR等[84]利用物模多波和各向异性性质反演地层主应力;TIGREK[63]首先利用反射系数反演获得动态参数,然后利用动静态参数之间的关系求得地质力学模型的参数,最后基于地质力学模型求得地应力的分布;SAYERS[85]利用时移地震实现地应力预测;STARR[86]提出了利用地震数据估算闭合应力梯度的方法;HUNT等[87]利用曲率和杨氏模量对地下应力分布进行预测;GRAY[88]考虑了裂缝引起的地下介质各向异性特征,通过建立HTI介质岩石力学模型对HTI介质地应力分布进行了预测,实现了基于地震数据的应力预测。何英[89]推导了基于曲率分析的构造应力场计算公式,利用曲率估算地层的构造应力,克服了构建复杂构造应力场模型的困难;张广智等[90]通过先验信息建立地层岩石物理模型,基于该模型获得地下介质刚度矩阵,根据刚度矩阵计算地下介质应力分布;宗兆云[91]提出了利用裂缝岩石参数预测地应力的方法;马妮等[92-93]同时考虑HTI介质垂直裂缝的影响和VTI介质水平层理的作用,基于正交各向异性介质理论,推导了正交各向异性(OA)介质的地应力表达式,并利用方位叠前地震数据实现了地应力的地震预测;熊晓军等[94]通过叠前地震资料反演、速度分析和层位数据获得地下介质弹性参数、层速度和水平方向构造应变,从而计算得到地应力分布。以下从反射系数反演、地震曲率属性和岩石物理建模三个方面阐述基于地震资料的地应力预测方法。

4.1 基于反射系数反演的地应力预测

TIGREK[63]通过分析PP波反射系数和PS波反射系数大小与地应力之间的关系,建立了如下目标函数:

(22)

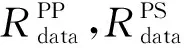
TIGREK指出,地下介质的静态参数可以更好地反映地下介质的应力状态,应该先通过实验测量获得目标区动静态参数比,在反射系数反演的基础上获得静态参数,然后利用静态参数建立地质力学模型,最后基于该模型计算得到地下介质的应力分布。

4.2 基于曲率属性的地应力预测

地层曲率与应变有着密切的关系,胡克定律将应变与应力联系在一起。HUNT等[87]建立了地层曲率与地应力之间的关系,即:

(23)

式中:E为杨氏模量,Kc为曲率属性,h为褶皱岩层的厚度,e为应变,σ为应力。将公式(23)进行简化可得:

(24)

由(24)式可知,利用杨氏模量和曲率的乘积可近似表征地层的应力属性,为裂缝密度的预测提供可靠的依据。

何英[89]在薄板理论的假设下,推导得到基于曲率的地应力表达式。如图2所示,在直角坐标系中,设薄板中面为z=0的坐标面,沿x,y正方向的位移分别为ux,uy,沿z方向的位移为扰度w(x,y),则:

式中:σx,σy和τxy分别为x,y轴方向上的主应力和xy面的切应力;Kx,Ky和Kxy分别为x,y方向的曲率和xy面的扭率;E,υ为杨氏模量和泊松比;t为地震剖面上应变介质上下界面的时差。主应力及其方位为:

式中,σmax为最大主应力,αt为σmax与x轴的夹角。通过地震反演获得地下介质杨氏模量和泊松比,由地震层位数据计算出曲率属性[95],便可预测地下介质的地应力分布。

熊晓军等[94]也给出了基于曲率的地应力预测方法:首先利用地震资料反演地下弹性参数杨氏模量和泊松比;然后利用地震资料和速度分析获得地下介质层速度,进而计算得到地层压力;接着利用叠前地震资料和层位数据计算曲率属性,利用曲率属性计算出水平方向构造应变;最后将以上计算结果代入线性各向同性组合弹簧模型,预测地下应力分布。

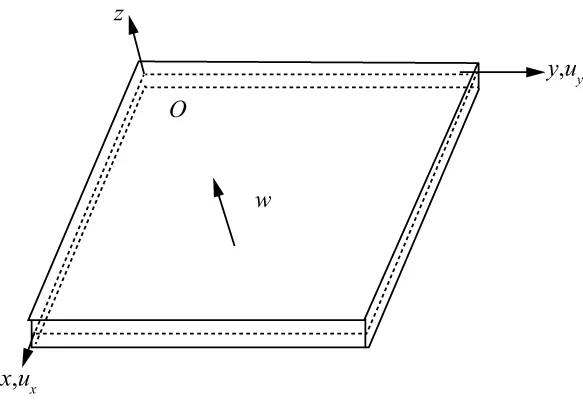
图2 薄板示意[89]

4.3 基于岩石物理模型的地应力预测

岩石物理模型建立了地震数据与储层参数的联系。通过对地震资料以及其它地质、测井资料进行综合分析,获得工区孔隙度、岩性等物性参数,基于此建立岩石物理模型,便可获得地下介质的刚度矩阵,从而实现地应力分布的预测。张广智等[90]对基于岩石物理模型的地应力预测进行了研究。以页岩为例,首先根据地震资料以及其它先验信息,对工区矿物、孔隙度等参数进行综合分析,建立岩石物理模型(图3)。然后基于岩石物理模型计算得到地下介质的刚度矩阵以及纵横波速度等。由于页岩可看作VTI介质,因此可以利用VTI介质模型进行地应力预测。SUAREZ-RIVERA等[96]给出了VTI介质地应力计算公式。

图3 页岩岩石物理等效模型构建[90]

式中:σv为垂直方向的地应力;ρ(h)为随深度变化的地层密度;g为重力加速度;H为测点深度;σH,σh分别为水平方向最大、最小地应力;Eh,Ev为水平方向和垂直方向的杨氏模量;υh,υv为水平方向和垂直方向的泊松比;pp为孔隙压力;εH为水平方向的构造应变。刚度矩阵可以转换成杨氏模量和泊松比,转换后代入(30)～(32)式,实现地应力预测。

根据地下介质的类型,选择相应的地应力计算模式:SAYERS[97]、GOODWAY等[98]、PEREZ等[99]提出的各向同性介质地应力计算方法;SUAREZ-RIVERA等[96]、GRAY[88]、邓金根等[100]给出的线性弹性TI地层地应力计算公式;马妮等[92-93]推导的正交各向异性介质地应力计算公式。GRAY[88]提出一种新的基于各向异性岩石力学模型和地震反演估算地应力的方法,利用岩石力学参数和地层各向异性参数计算地层的主应力:

同时,利用最大水平地应力和最小水平地应力的差异比,即水平应力差异比(differential horizontal stress ratio,DHSR),来衡量储层中容易压裂成网的区域。其公式为:

(35)

式中:σv为垂直方向的地应力;σH,σh分别为水平方向最大、最小地应力;E表示杨氏模量;υ表示泊松比;ZN表示法向柔度。DHSR是指示储层是否易于压裂成网的重要因子,当DHSR为低值时,其所在区域进行水力压裂时容易形成裂缝的网状结构;当DHSR为高值时,其所在的区域进行水力压裂时容易被压裂成定向排列的裂缝,有利于储层中油气的运移和非常规储层的开采。但是该方法基于HTI介质,没有考虑介质的水平层理影响,而实际页岩具有很强的水平层理特征。针对这个问题,马妮等[92-93]根据实际页岩储层的各向异性特征,同时考虑页岩气地层VTI和HTI特征的作用,利用正交各向异性介质岩石物理关系推导了正交各向异性介质的地应力精确计算公式:

式中,sij为OA介质的柔度系数。利用最大水平地应力σH和最小水平地应力σh,可以得到正交各向异性水平应力差异比精确公式(orthorhombic differential horizontal stress ratio,ODHSR):

(38)

根据柔度系数sij与弹性系数cij的关系,可以得到弹性系数表示的正交各向异性水平应力差异比:

(39)

正交各向异性介质的弹性矩阵有9个相对独立的弹性参数,利用TSVANKIN[101]提出的表征OA介质的各向异性参数公式,得到各向异性参数表示的弹性系数,将其代入(39)式得到最终的ODHSR公式。由于地应力精确公式过于复杂不便于实际应用,因此利用线性滑动理论对其进行近似简化:

(40)

(41)

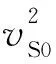
(42)

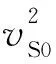
HTI介质方位弹性阻抗公式为:

(43)

式中,a=(1+tan2θ),b=-8g2sin2θ,c=(1-4g2sin2θ),d=sin2θcos2φ(1+tan2θsin2φ),e=cos4φsin2θtan2θ,f=-8g2sin2θcos2φ;θ为地震数据入射角,φ为地震观测方位角;α0,β0和ρ0分别为依据测井数据获得的纵波速度、横波速度和密度平均值;α,β和ρ分别为测井获得的纵波速度、横波速度和密度,ε(V),δ(V)和γ(V)分别为HTI介质的各向异性参数。

将公式(43)两边同时取对数使其线性化可得[102]:

(44)

式中,IE0=α0ρ0。然后建立方位弹性阻抗与裂缝型储层岩石弹性参数之间的方程组:

(45)

将上式改写为矩阵的形式:

(46)

根据测井获得的纵波速度、横波速度、密度以及各向异性参数和井旁道对应各采样点的方位弹性阻抗,求解上述方程得到系数矩阵的各个元素(在储层弹性性质横向变化较小的情况下,可将系数矩阵中的常系数看作是恒定不变的值);然后将反演得到的方位弹性阻抗数据体代入,便可求得工区纵波速度、横波速度、密度以及各向异性参数;接着利用HTI介质与VTI介质各向异性参数之间的关系[103]

(47)

求得VTI介质各向异性参数γ;最后将反演得到的弹性参数和各向异性参数代入公式(42)计算得到正交各向异性水平应力差异比。

选取某工区实际资料进行地应力的地震预测。首先利用6个不同方位、不同入射角的方位叠前地震数据进行叠前方位弹性阻抗反演。如图4所示,不同方位、不同入射角的方位地震数据同相轴相似,但彼此间存在着明显的差异,即地震数据的振幅属性随着方位角和入射角的不同而不同。

图4 某工区不同方位部分角度叠加道集(纵横测线剖面和层切片)[93]

利用叠前方位地震反演得到的弹性阻抗数据体提取储层的弹性参数和各向异性参数,即所需的纵波速度、横波速度、密度和HTI介质的各向异性参数,如图5所示。

根据HTI介质与VTI介质各向异性参数的关系,得到VTI介质各向异性参数,如图6所示。

最后基于ODHSR近似公式,利用叠前方位地震反演方法获得的弹性参数和各向异性参数,计算得到某个区域连续的ODHSR剖面,实现基于正交各向异性介质的地应力地震预测,如图7所示。

由图7可以看出研究区ODHSR值的分布情况,根据ODHSR值的高低可以识别储层中容易压裂成网的区域。在ODHSR低值的区域进行水力压裂容易形成网状裂缝结构,有利于油气的聚集和运移,同时,应该综合应用其它反映岩石脆性、物性和可压缩性等参数[104-110]来指导油气勘探开发。

图5 弹性参数和各向异性参数反演结果(纵横测线剖面和层切片)[93]

图6 VTI介质的各向异性参数(纵横测线剖面和层切片)[93]

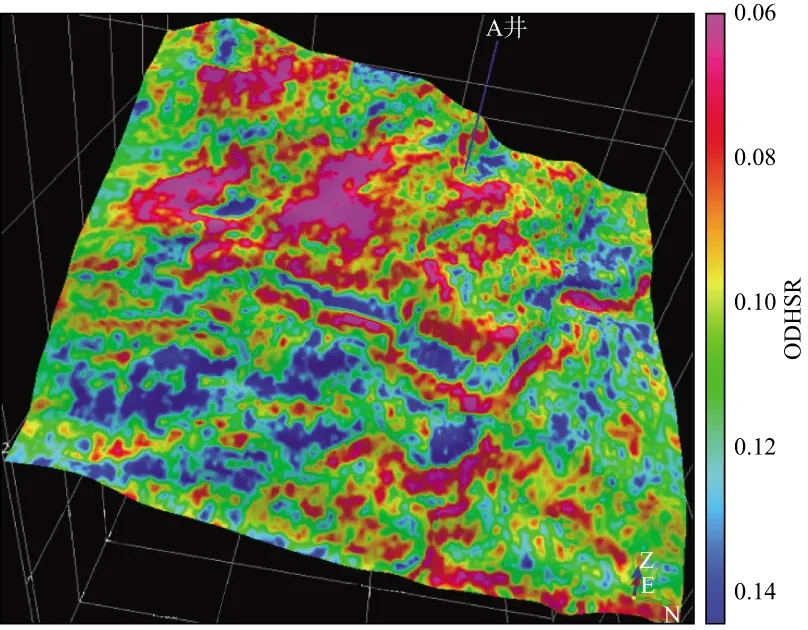
图7 ODHSR的层切片[93]

5 认识与展望

页岩气储层的低孔低渗特点决定了需要对其进行水力压裂改造以形成油气储集和运移的裂缝,而地应力是决定裂缝延伸方向、形状和大小的决定性因素之一,地应力的研究对于油气田的勘探开发有着重要的意义。本文从地应力测量方法、地应力测井计算方法、地应力数值模拟方法及地应力地震预测方法四个方面介绍了地应力的预测方法,以利于人们系统地认识和了解地应力预测方法。地震技术是识别与评价页岩气储层的核心技术之一,如何利用地震数据进行地应力预测是我们研究的重点。介绍了基于反射系数反演的地应力预测、基于曲率属性的地应力预测和基于岩石物理模型的地应力预测方法,其中提到了水平应力差异比(DHSR)的概念,它是储层进行水力压裂时容易产生网状裂缝的区域指示因子,能够指导油气田的勘探与开发。在未来的地应力地震预测方法研究中,还需要考虑构造应力、孔隙压力等参数对地应力的影响。关于如何利用地震技术估算这些参数用于校正地应力、如何推导出更加准确的地应力地震预测计算公式、如何在实际资料中更好地应用这些理论和方法等研究,还有很长的路要走。地应力的预测准确与否,直接影响着储层裂缝密度预测的准确性、井位部署的合理性及钻井优化设计的完善性等,因此如何在理论方法及生产实践中探索出更好的地应力地震预测方法是我们今后需要研究的重点方向。