一种补偿介质吸收叠前时间偏移技术

陈树民,刘礼农,张剑峰,裴江云,陈志德,王 成

(1.中国石油天然气股份有限公司大庆油田有限责任公司勘探开发研究院,黑龙江大庆163712;2.中国科学院地质与地球物理研究所中国科学院油气资源研究重点实验室,北京100029)

地震波传播过程中,一部分能量会转化为热能,相应的地震波的幅值产生衰减效应,该过程称为吸收。地震波不同频率成分的幅值衰减是不同的,频率越高,衰减越快,这是因为高频成分的波长相对低频成分的波长较短,对于一个固定的传播距离,相当于低频成分少个波长,高频成分则多个波长,而地震波每传播一个波长的距离,能量损失的程度恒定。这也导致接收到的反射地震资料的有效频带随反射深度增大逐渐变窄;而不同频率成分以不同的速度传播,也导致了地震子波的频散,且反射层位越深,频散越严重。由于常规偏移方法没有补偿黏性吸收导致的幅值衰减,也没有校正频散,因而使得偏移成像结果的分辨率较低,反射层位越深,分辨率越低。油气勘探中,对薄砂体、小断层的识别是认识油气疏导体系、识别有利储层的重要环节。因此,在油气勘探中,提高地震成像分辨率一直是反射地震资料处理过程中的一个重要研究内容。

提高地震成像分辨率的方法很多,包括针对叠后剖面的谱白化反褶积[1]、非稳态反褶积[2-3]、基于统计假设或测井资料的各类拓宽频带技术以及反Q滤波[4-5]和黏弹性叠前深度偏移[6-8]等。谱白化反褶积可在有效频带内将振幅谱拉平,但其提高分辨率的效果较大程度上依赖于是否获取了合适的参数[1]。各类拓频技术通过引入地震记录以外的信息来提高地震方法的分辨率,在获得更高视分辨率的同时,也需对地震数据基本频带进行提高信噪比的处理;此外,各类拓频技术使用的前提是地震记录的子波是时不变的,因此即使应用此类技术,也必须在预处理中首先补偿地震波的吸收衰减,实现地震子波的一致性[9]。

非稳态反褶积是针对黏性吸收导致的地震分辨率降低而发展的提高分辨率方法。该方法基于严谨的物理基础,但在估计空变的非稳态子波方面存在较大困难,且通常不能同时实现频散校正。目前,非稳态反褶积仅在叠加剖面上能得到较好应用效果。稳定性和噪声放大是该方法在实际应用中面临的问题。

反Q滤波可同时应用于叠前和叠后地震资料。该方法从补偿地震波幅值的黏性吸收出发,具有坚实的物理基础。反Q滤波应用于叠前地震资料时忽略了地震波传播路径对幅值衰减的影响,用于非均匀Q值模型时存在较大误差;应用于叠后地震资料时可处理层状Q值模型情况,但由于叠加过程已将不同偏移距或者入射角的地震道进行了叠加,此时,应用反Q滤波是将存在不同程度吸收衰减的幅值作同一处理,因而并不能完全消除吸收衰减的影响。

为了补偿地震波吸收衰减,提高地震成像分辨率,在偏移成像过程中恢复地震波被衰减的高频成分是提高地震成像分辨率的关键。恢复地震波被衰减的高频成分可真正地提高地震勘探方法对小断层和薄砂体的识别能力。

黏弹性叠前深度偏移准确考虑了地震波的传播和黏性衰减过程,理论上可较好地补偿地震波的黏性吸收,但黏弹性深度偏移方法需要深度域地层Q值模型,难度更大,因此黏弹性深度偏移的实际应用还存在较大的困难。

叠前时间偏移是叠前偏移成像中的另一种重要方法。该方法可对断层较为复杂但速度横向变化不是很剧烈的地质构造进行较好的成像。与叠前深度偏移方法相比,除具有较高的计算效率外,其主要优点是只需使用叠加(均方根)速度,这样可简单地通过速度扫描等方式得到合适的偏移速度模型,回避了使用叠前深度偏移方法面临的层速度建模困难的问题。因此,叠前时间偏移方法已成为地震勘探领域广泛应用的关键技术之一。但现在常用的叠前时间偏移方法不具有补偿地震波吸收衰减的能力,所以如何结合叠前时间偏移过程恢复地震波被衰减的高频成分,成为一个具有重要应用价值的问题。

近年来,通过结合叠前深度偏移和叠前时间偏移方法,人们提出了一系列基于等效参数的广义叠前时间偏移方法[10-13],在叠加速度的基础上引入新的等效参数,拓宽了现行叠前时间偏移方法解决实际复杂问题的能力和范围。通过引入第二个描述黏性吸收的等效Q值参数,提出了可直接补偿吸收衰减的叠前时间偏移方法[11-12],用较简单的技术方案实现了补偿地震波传播过程中吸收衰减的目标。本文详细阐述了这一结合叠前时间偏移过程恢复地震波被衰减的高频成分的方法,以及在保持偏移计算稳定性、介质吸收参数建模、补偿噪声压制以及计算效率提高等方面提出的一系列技术方案。

1 补偿介质吸收叠前时间偏移

在提高地震数据分辨率的研究中,通常假定品质因子Q与频率无关或者随频率弱变化[14],这便是恒Q模型,在地震学观测频率范围内(0.001～100.000Hz),Q值可以近似看作常数。基于此,引入复速度c(ω)与实速度vr(ω)表达式[15]:

式中:ω是角频率;ωc是高截频;j为虚数单位。当频率趋向于ωc时,实速度将趋近于常值。在此,用主频ω0来代替高截频ωc,原因在于主频对应的实速度恰是我们通过速度估计方法可以得到的。作如下代换和近似:

(2)

将(2)式代入(1)式得:

(3)

式中:v为常规的偏移速度;Q代表与频率无关的恒Q值。

若将单个地震道看作是仅有一个接收道的单炮记录,则其炮域偏移的炮点至成像点的正传波场为[11]:

(4)

检波点至成像点的反传波场为:

(5)

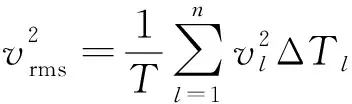
实际上,我们无法知道准确的S(ω),而现行的处理流程中的反褶积处理可以认为是已剔除了S(ω)·[ω/(2π)]exp(jπ/2)这些有关震源子波的影响。因此,忽略震源子波的影响,应用反褶积成像条件,可得单道数据的成像结果,也即脉冲响应,即:

(6)

式中:(τs/τg)2是成像权系数,它补偿了地震波的球面扩散影响。公式(6)表明,成像点处的等效Q值唯一决定该点的成像幅值。因此,我们可以采用类似于确定均方根偏移速度的方法,用扫描方式来确定该点的等效Q值。

(7)

式中:f′(t)为该地震道的一阶导数。

当Qeff不随时间深度和水平位置变化时,若假设:

(8)

则(6)式可写为:

(9)

由(8)式可知,G(t)恰好是该地震道的反Q滤波结果。(9)式表明,“反Q滤波+叠前时间偏移”是补偿吸收衰减的偏移方法在均匀Q值情况下的特例。这为我们应用扫描方法快速建立等效Q值模型提供了理论基础。

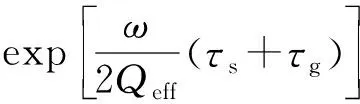
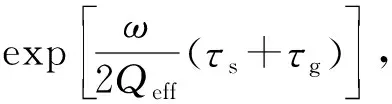
φ(η)=exp(η),η≤lnG

(10a)

φ(η)=G[1-lnG-2.5(lnG)2]+G(1+5lnG)η-

2.5Gη2, lnG<η≤lnG+0.2

(10b)

φ(η)=1.1G,η>ln(G)+0.2

(10c)

式中:η=ω(τs+τg)/(2Qeff);G为给定的阈值。

2 等效Q值估计

Q值估计涉及到随频率变化的幅值,与偏移速度估计相比困难得多,目前主要是利用透射波的信息求取,即利用上行波的VSP测井资料或者井间资料,根据主频移动、频谱形状等信息确定Q值。在实际应用中,其局限性很明显:通常情况下,地震勘探目标工区的井资料有限,难以建立非均匀的Q值模型,此外,Q值是一个与地震信号主频相关的变量,将依据透射资料得到的Q值模型应用到反射地震资料时,因为地震反射波与透射波主频不同,还需做进一步校正。为此,我们发展了利用反射资料根据补偿效果和频带宽度确定等效Q值的方法。

由(9)式可知,“反Q滤波+叠前时间偏移”是补偿吸收衰减的叠前时间偏移方法在均匀Q值情况下的特例,而其计算量仅是后者的几十分之一,我们只需对预先给定的等效Q值序列分别进行“反Q滤波+常规叠前时间偏移”计算,就可得到进行等效Q值扫描的基础数据集。而在实际地震处理中确定合适的等效Q值时,往往是在信噪比可接受的前提下追求频谱的最宽,因此,在每一分析时窗内,我们以频谱的最宽化作为等效Q值选取的准则。

具体来讲,在每个等效Q值拾取窗口,对系列Q值中的Qi,从其成像剖面最终结果中计算频谱包络,拾取-20dB对应的最大和最小频率f1a和f1b(工业中通常认为-20dB以下的信号不再有效,这一分贝值在软件实现时可作为参数由用户设置)。为了防止-20dB遇到频谱凹陷,采用分贝区间[d1,d2]代替-20dB点。区间[d1,d2]包含-20dB,d1和d2围绕-20dB上下分布,如果频谱上下震荡比较剧烈则d1和d2波动也较大,将区间等间距的分为N份,那么第i个点值是d1i=d1+(i-1)×(d2-d1)/(N-1),此时-20dB对应的最大、最小频率即为di对应的频率平均值。

(11)

式中:f1ai,f1bi分别表示d1i对应的最大、最小频率。同样,设f2a和f2b分别表示-10dB对应的最大和最小频率,用区间[d3,d4]代替-10dB点,区间等间距分为N份,第i个点值为d2i=d3+(i-1)×(d4-d3)/(N-1)。那么-10dB对应的最大、小频率即为di对应的频率平均值。

(12)

式中:f2ai,f2bi分别表示d2i对应的最大、最小频率。

从小偏移距的部分偏移叠加剖面的频谱包络中,拾取-10dB对应的最大和最小频率f2a1和f2b1,从大偏移距偏移叠加剖面的频谱包络中,拾取-10dB对应的最大和最小频率f2a2和f2b2,计算频率偏差;基于f1ai,f1bi和f2ai,f2bi得到4条随1/Q变化的曲线,首先厘定较小的区间,在该区间中,主要观察-20dB对应的高、低频曲线,寻找将高频提高得最多同时低频损失较少的那个Q值,这样才能确定Q值达到了提高有效频带的目标,最终确定该Q值窗中心处的Q值。如图1所示,这是某一窗口的高、低频曲线,两条红线(或蓝线)之间的宽度就是-20dB(或-10dB)对应的频谱宽度。图1中,绿线对应的横坐标表示所确定的Q值,此时高频较高,同时低频损失较少。

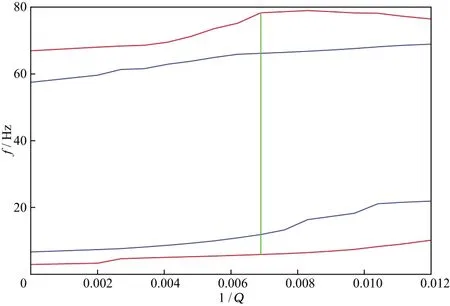
图1 某一分析时窗不同分贝下的频带曲线 图中,红线为-20dB对应的最大、最小频率随1/Q变化的曲线，蓝线为-10dB对应的最大、最小频率随1/Q变化的曲线。

3 结合稳相偏移方法压制偏移噪声

针对偏移噪声压制,基于菲涅耳带叠加实现偏移成像就是一个最佳选择,这也是各类偏移方法一直努力的目标[16-18]。由于实际地质构造中速度和反射界面的复杂性,直接从地质模型出发估计准确的菲涅耳带几乎不可能实现。针对这一问题,我们在偏移过程中构建倾角域偏移道集,直接将菲涅耳带形象地展示在这一偏移道集中,可容易地从中确定菲涅耳带。

3.1 倾角道集

如图2所示,I为成像点,s和g分别代表炮点和接收点,v和vrms分别为成像点I处的层速度与均方根速度,n为反射界面法向量,p和q分别为成像点I处的入射向量和反射向量,dx和dy分别为反射界面与xOz平面和yOz平面的交线。定义反射界面在xOz平面的视倾角为θx,其旅行时相关的视倾角为φx;反射界面在yOz平面的视倾角为θy,其旅行时相关的视倾角为φy,则有:

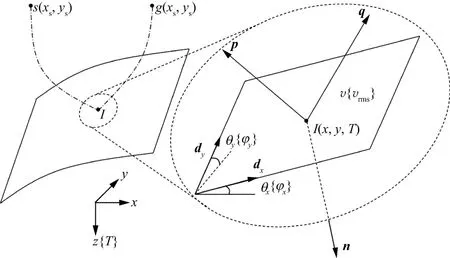
图2 倾角道集计算示意

若在每一成像点,不考虑偏移距,仅将偏移结果按φx和φy的大小进行分选和叠加,就可在每个水平位置(即CRP点)形成一对分别针对沿测线方向倾角和与测线垂直方向倾角的一维倾角域偏移道集I(x,y,T0,φx),I(x,y,T0,φy):

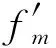
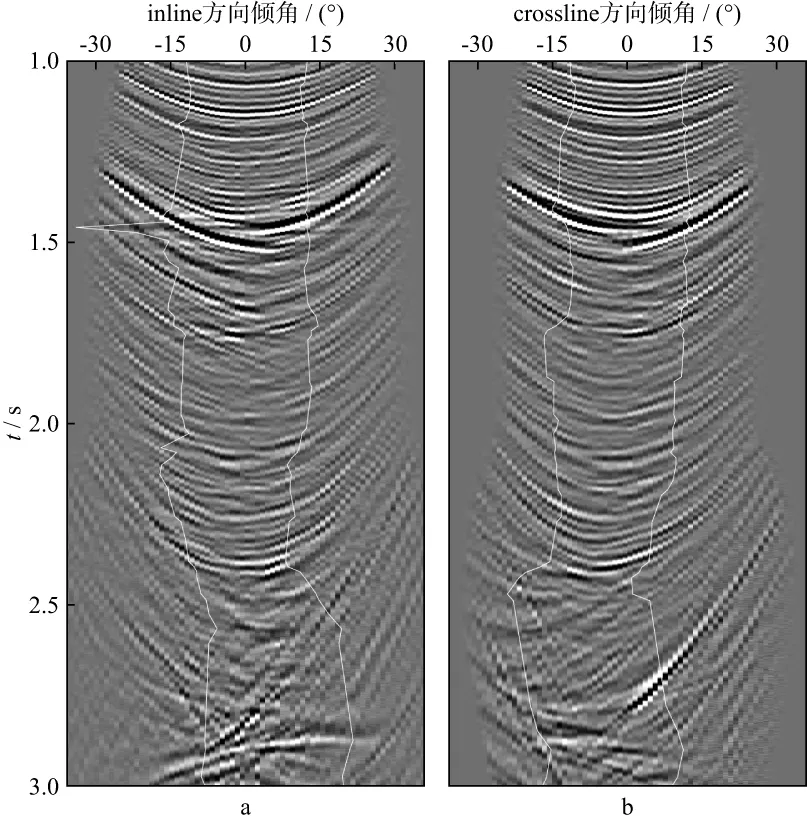
图3 某CDP点的inline方向(a)与crossline方向(b)的倾角道集(图中白线为拾取的菲涅耳带边界)

3.2 结合稳相偏移压制噪声

在三维补偿介质吸收叠前时间偏移计算中,通过计算拟成像反射界面的倾角来判断倾角是否在菲涅耳带内,若在菲涅耳带内,则参与稳相叠加,从而实现稳相叠前时间偏移。这样,可保证仅是菲涅耳带内的结果参与偏移成像。如此,既可避免常规偏移中采用较小的偏移孔径导致的陡倾角构造成像缺失,又可避免采用过大的偏移孔径带来的偏移成像低信噪比问题,实现基于菲涅耳带的最优孔径成像[12]。

与常规叠前时间偏移相比,稳相叠前时间偏移在对每一地震道的偏移计算中,先利用倾角公式((13)式和(14)式)计算在每一成像点处的与旅行时相关的倾角,同时读取该成像点的菲涅耳带在两个倾角方向上的上、下界角度。当该地震道在这一成像点处的与旅行时相关的倾角在菲涅耳带内时,将计算结果累加到存放成像点I(x,y,T0)上,否则不参与成像,这样可得到仅对倾角域偏移道集中的菲涅耳带部分叠加成像的高信噪比偏移结果。图4给出了未结合和结合稳相算法的补偿介质吸收叠前时间偏移成像的水平切片,可以看出,稳相偏移水平切片在保持构造形态不变的情况下信噪比得到很大提高。此外,需要指出的是,稳相偏移不但可以实现合理的偏移孔径空变以得到复杂构造高精度精细成像结果,而且还可以提高偏移计算的效率。图4所示的补偿介质吸收叠前时间偏移计算实例,结合稳相偏移方案可节约30%左右的计算时间。

图4 叠前时间偏移的水平切片a 结合稳相算法的补偿介质吸收; b 未结合稳相算法的补偿介质吸收

4 基于GPU加速和异步双缓存的并行计算

补偿介质吸收叠前时间偏移是在频率域内进行,较常规时间域偏移而言,计算量明显增加。增加的计算量主要体现在两个方面:一是频率域的补偿算法包括相位校正、振幅补偿,且这些计算大多都是对数和指数运算,对应多个计算机指令,耗时较长;二是与常规叠前时间偏移相比,这一偏移算法在频率域进行,幅值信息必须将所有频率成分分别计算得到的结果累加。因此,我们基于GPU技术提高其计算效率[19-21]。

由于实际三维地震资料数据量庞大,地震道数多,采用前文所述的单道成像方案会使数据在CPU和GPU之间频繁拷贝,而且数据处理的前置准备工作也不可避免,其中包括数据从硬盘读入内存、导数求取、能量调节等,针对单个地震道而言,这些环节和核心成像过程必须串行,并行效率低。为此,我们提出采用多流技术的异步双缓存方案,该方案是在原始单道成像基础上,采用单次批量进入多道数据,多条成像线结果输出。这样在GPU进行成像计算时,由于异步执行,所以CPU是就绪状态的,可以准备第二道数据的前置计算,这样就使得CPU的前置工作和实际GPU成像(频率域累加)并行执行。对用户而言,隐藏了CPU的工作时间,使得GPU可以充分发挥其计算性能,将必要的CPU工作掩盖在GPU的工作过程中。

由于拷贝和核函数的异步执行可能会导致程序中不同流之间成像孔径的计算拷贝及成像计算产生错误,因此,我们提出了双缓存方案。通过增加一个变号器,在每一次异步拷贝时用变号器控制成像孔径拷贝,保证了随后成像计算的正确进行。

5 大庆油田实际应用

为推动补偿介质吸收叠前时间偏移技术的工业应用,我们集成上述理论研究成果,开发了一套大规模实用化的地震叠前高分辨率成像GPU软件系统,解决了应用中面临的参数选择、数据多样性、资料噪声、海量数据存取与计算以及鲁棒性等问题。该偏移成像方法已在大庆油田广泛应用,及时有效地指导了大庆油田扶余油层致密油的勘探部署。

大庆油田扶余油层以陆相河流—三角洲沉积体系为主,埋深超过1500m,砂体厚度薄(单层厚度2～5m),横向速度变化快(河道宽度小于600m),扶余油层致密油水平井勘探主要针对2～5m单砂体。上覆地层为砂泥岩薄互层,地层压实程度低、非均质性强。上覆地层对地震波的吸收是影响地震资料分辨率和保真度的关键因素。

图5为永乐工区1085线常规叠前时间偏移剖面和补偿介质吸收叠前时间偏移剖面。图5中方框区域放大结果如图6所示。可以看出,本文方法有效消除了地层吸收衰减的影响,提高了地震资料的纵向分辨率,从而提高了该区地震资料刻画薄储层的能力。图7 为放大结果对应的频谱,可以看出,补偿介质吸收叠前时间偏移在振幅-20dB处频谱展宽20Hz。

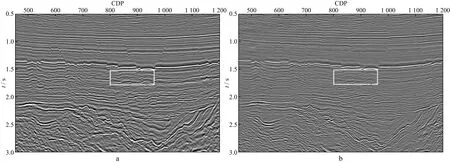
图5 常规叠前时间偏移(a)和补偿介质吸收叠前时间偏移(b)剖面对比

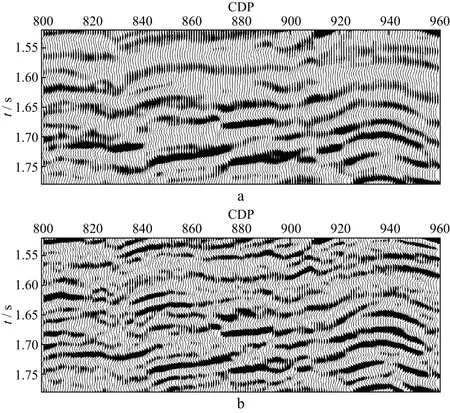
图6 常规叠前时间偏移(a)与补偿介质吸收叠前时间偏移剖面(b)局部放大显示

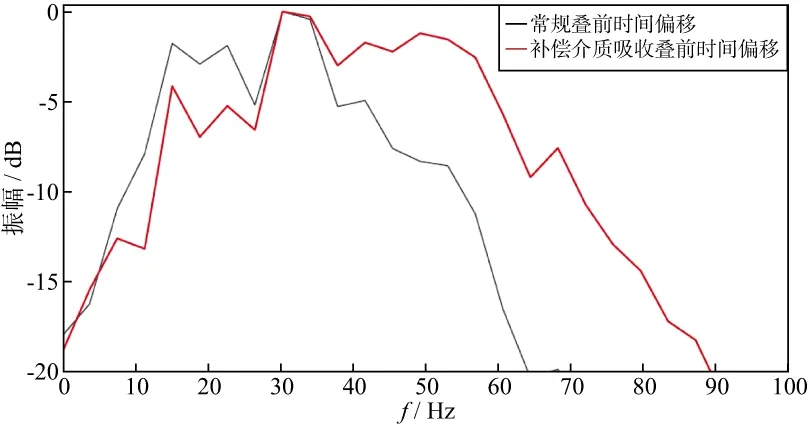
图7 常规叠前时间偏移与补偿介质吸收叠前时间偏移剖面局部放大结果对应的频谱分析曲线

大庆油田三肇地区扶余油层垂向上在T2反射层以下100ms之内,是目前致密油勘探水平井部署的重点区域。图8是针对扶余油层3～5m甜点目标部署的水平井ZP15井的常规叠前时间偏移剖面与补偿介质吸收叠前时间偏移剖面。部署的主要参考直井为Z9-38井和Z57-F1井,甜点层在剖面1.48s的位置,地震反射特征对应中强反射轴。在水平井轨迹的位置(A,B,C,D分别代表水平井轨迹4个控制点,A点为入靶点)。常规叠前时间偏移剖面上,扶余油层的频带为6～70Hz,垂向分辨率低,不能识别位于T2反射下波谷内的F11-3油层组目标砂岩。补偿介质吸收叠前时间偏移剖面上扶余油层的频带为6～90Hz,垂向分辨率提高,F11-3油层组目标砂岩对应于T2反射下的第一个波峰位置,可以连续追踪。振幅横向变化能够反映砂体厚度的横向变化。依据补偿介质吸收叠前时间偏移成像资料,指导了ZP15井水平井钻探,ZP15井在A靶点准确入靶,水平段长度1050m,其中,砂岩1010m,泥岩40m,砂岩钻遇率达93.16%。

补偿介质吸收叠前时间偏移成像方法已在大庆油田累计完成16个三维井区合计590km2的目标处理,提交16口水平井部署设计,已实施的9口水平井均准确入靶,水平段平均砂岩钻遇率达到86.0%,比前期应用常规偏移结果提高了15.1%,油层钻遇率提高了14.4%,有效地支撑了大庆油田扶余油层致密油勘探。

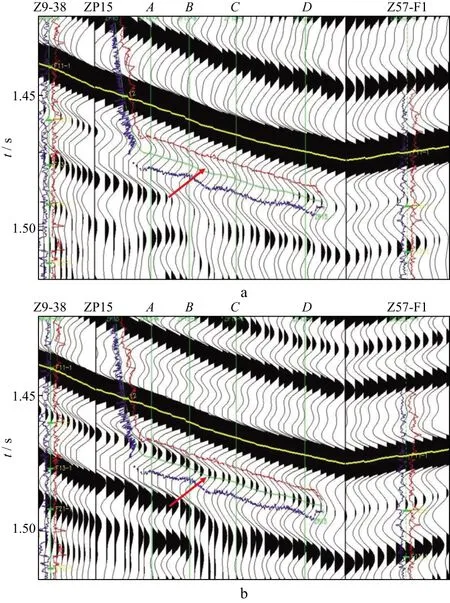
图8 常规叠前时间偏移(a)和补偿介质吸收叠前时间偏移(b)过ZP15井剖面

6 结论

本文介绍了补偿介质吸收叠前时间偏移技术及其在大庆油田的应用实践。等效Q值参数的引入和对应的基于地表观测数据的等效Q值建模方法,解决了黏性偏移应用中的Q值模型建模的困难;利用黏性补偿因子的阈值稳定性控制方法,解决了黏性吸收补偿的稳定性问题。将基于倾角道集的稳相(菲涅耳带叠加)偏移方案结合到黏弹性叠前时间偏移方法中,有效地解决了黏性补偿导致的偏移噪声放大问题;而偏移实现GPU算法的优化也较大程度地提高了这一补偿算法的计算效率。大庆油田多个三维实际地震资料的处理结果证实,本文方法在保持反射振幅关系的前提下展宽地震频带20Hz,有效提高了地震资料的垂向分辨率,是松辽盆地中浅层薄互层地质条件下高分辨率成像的有效技术。