基于支持向量机的交互检验储层预测

张向君,张 晔

(1.大庆钻探工程公司物探研究院,黑龙江大庆163357;2.东北石油大学,黑龙江大庆163318)

支持向量机(SVM)是一种基于统计学习理论的学习方法[1],在理论研究和实际应用两个方面均已成为人工智能和机器学习领域的热点[2]。支持向量机方法最早是针对模式识别问题提出来的,随着VAPNIK等对ε不敏感损失函数的引入[3],支持向量机应用由模式识别领域推广到回归估计领域,并展现出很好的学习性能,在建模、预测等方面取得了很好的效果[4-7]。支持向量机方法在理论上能够保证找到的极值解就是全局最优解而非局部最小值,因此对未知样本有较好的泛化能力[8]。

在地震储层预测中,常用的储层参数预测方法大多建立在线性模型基础上,是对实际模型一定程度上的近似,而一些非线性方法则存在许多影响预测效果的问题[9]。支持向量机方法采用了与传统方法完全不同的思路,在井资料比较少的情况下也能够描述储层物性和地震数据之间的非线性关系,使得建立的预测模型具有较高的拟合精度[9-10]。充分发挥SVM的优良性能,提高储层预测精度,关键在于两个方面:一是样本的优选,样本优选的目的在于选出对储层敏感、彼此相关性不强的样本,舍弃那些对噪声敏感的样本[11-16];二是支持向量机的惩罚因子及核函数参数设置,这两个参数影响着支持向量机的泛化能力和储层预测精度。本文通过交互检验方法优选支持向量机的惩罚因子及核函数参数,提高支持向量机储层预测精度。

1 方法原理

1.1 支持向量机方法原理

给定样本集{(xi,yi),i=1,2,…,m},其中xi∈RN是输入值,yi∈R是对应的目标值,m是样本数,N是样本集的维数。定义ε不敏感损失函数为:

(1)

其中f(x)是通过对给定样本集的学习而获得的回归估计函数,y是x所对应的目标值,ε>0是与函数估计精度相关的参数。学习的目的是使构造的回归估计函数f(x)与目标值y的距离小于ε。

在样本集是非线性的情况下,可以通过非线性函数φ(x)将样本集数据x映射到一个高维的线性空间,在高维线性空间中完成回归函数的构建,即:

(2)

式中:ω是权值向量,b是偏置参数。

基于统计学习理论的结构风险最小化思想,支持向量机可以采用极小化优化模型来构建回归函数[2,17],即

(3)

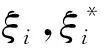
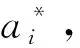
(4)

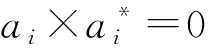
(5)

其中,

(6)

式中:NNSV为标准支持向量数量。由(5)式和(6)式知,非线性函数可以将样本数据从低维空间映射到高维空间,但在计算回归估计函数时只需计算核函数,并不需要显式计算该非线性函数,因此不会造成高维特征空间的维数灾难问题。选择核函数需满足Merce条件,本文选择径向基函数:

(7)

可见,在支持向量机计算过程中涉及到两个主要参数,即惩罚因子C和核函数参数g。

1.2 基于交互检验的参数优选方法

惩罚因子C用于控制目标函数中两项之间的权重,C取得过小或过大,都会使估计函数的泛化能力变差。若核函数参数g选得很小,则高次特征衰减得很快,实际上降低了空间维数;若g选得过大,则会出现过拟合现象。在实际应用中,对同一区块不同层位进行储层预测时,C和g的取值是完全不同的,即使是对同一层位进行储层预测,在不同区块C和g的取值也是不同的,而且没有规律可循。

本文通过交互检验选取参数C和g,优选步骤如下:

1) 初始化参数Cstart,Cend,ΔC,gstart,gend,Δg。其中,Cstart和Cend是参数C的优选范围,ΔC是参数C的优选步长,gstart和gend是参数g的优选范围,Δg是参数g的优选步长。

2) 将样本{(xi,yi),i=1,2,…,m}随机划分为均等的n组,令C=Cstart,g=gstart,k=1。

3) 令j=1。

4) 选取第j组作为检验样本,余下的n-1组作为训练样本。

5) 用(1)～(7)式计算损失函数|y-f(x)|的均方误差ej。

6) 令j=j+1,若j≤n,则转向步骤4),否则转向步骤7)。

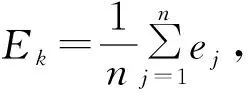
8) 令C=C+ΔC,k=k+1,若C≤Cend,则转向步骤3),否则转向步骤9)。

9) 选择最小误差minEk所对应的C和g为最优参数值。

2 应用实例

某油田开发区块P油层砂岩具有较好的物性,砂岩分布及砂岩厚度预测是该区块开发的关键。区块内有25口井,在P油层处的砂岩厚度均小于13m,将各井在P油层处的砂岩厚度及地震属性作为样本,用本文方法进行砂岩厚度预测。利用该区块三维地震资料提取了振幅、频率、相位等20种地震属性,采用基于核相似性度量的特征选择方法[11],优选出平均绝对振幅、功率谱总能量、功率谱峰值频率、瞬时相位等4种地震属性。为了验证储层预测效果,选用Well-sh401井、Well-sh29井、Well-sh60井作为后验井,将其余22口井及优选出的平均绝对振幅、功率谱总能量、功率谱峰值频率、瞬时相位等4种地震属性作为样本,用于砂岩厚度预测。参数C和g的选取采用交互检验的方法进行,取n=4,依照前述参数优选流程,计算得到最优C,g的值为:C=92,g=49。

图1是选用C=92,g=49时预测的砂岩厚度图。表1给出了后验井砂岩的实测值和图1的预测值,相对误差都在11.59%以下。若使用非优选出的参数C和g,砂岩厚度的预测精度就会受到影响。

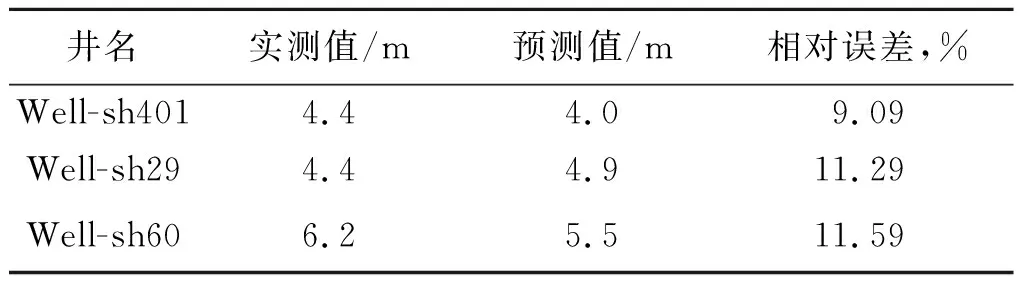
表1 图1砂岩厚度统计表

图2是非优选参数C=92,g=33预测的砂岩厚度图,预测精度有所降低。表2给出了后验井砂岩的实测值和图2的预测值,相对误差都大于13.64%。可见,通过交互检验优选参数C和g,可以提高储层砂岩厚度的预测精度。

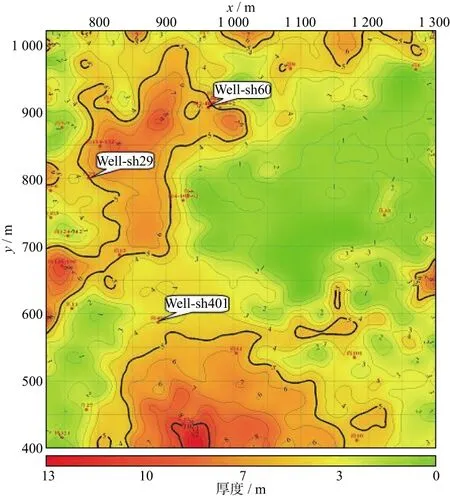
图1 砂岩厚度预测结果(C=92,g=49)

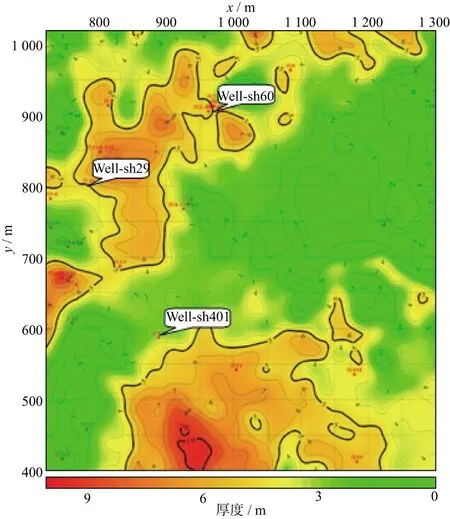
图2 砂岩厚度预测结果(C=92,g=33)

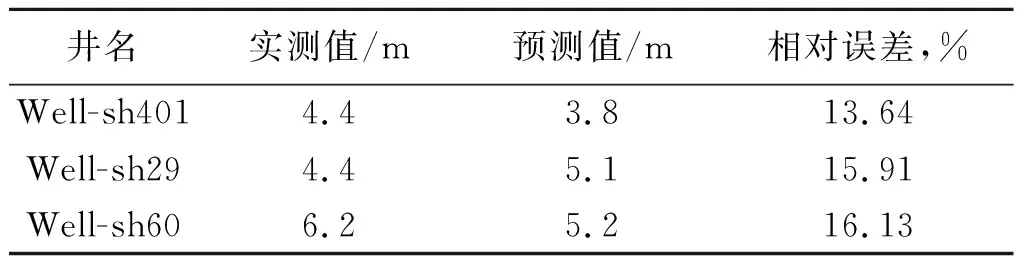
井名实测值/m预测值/m相对误差,%Well-sh4014.43.813.64Well-sh294.45.115.91Well-sh606.25.216.13

3 结论

支持向量机是有限样本情况下的机器学习方法,具有较好的学习、预测性能。支持向量机应用于储层预测时,惩罚因子及核函数参数的设置非常关键,设置过大或过小都会降低储层预测的精度。通过交互检验优选支持向量机的惩罚因子及核函数参数的方法在地震储层预测中具有较好的实用性,能够提高储层预测精度。