基于压缩感知的地震数据重建
舒国旭,吕公河,吕 尧,石太昆,邸志欣,霍守东
(1.油气资源研究院重点实验室,中国科学院地质与地球物理研究所,北京100029;2.中国科学院大学,北京100049;3.中国科学院地球科学研究院,北京100029;4.中石化石油工程地球物理有限公司,北京100020;5.中石化石油工程地球物理有限公司研发中心,北京100020)
传统的地震数据采集遵循Shannon-Nyquist采样定理,即:若要使采集到的数据能不失真地保持原信号中的信息,采样频率必须是原信号频带宽度的两倍以上。随着地震勘探目标日趋复杂,对于地震成像的精度要求越来越高,需要采集更高质量的地震数据。“两宽一高”地震数据采集技术在提高地震资料品质,改善复杂构造区成像质量方面有着明显的技术优势。然而,在应用该技术的同时也意味着激发点以及采集道数的急剧增加,在采集时间大大增加的同时也使得采集成本急剧增加。此外,由于勘探工区地表环境的影响,比如河流、村庄和道路等,使得我们往往无法根据设计的观测系统布置炮点及检波点,也就无法采集到完整的地震数据,进而影响后续的地震成像及解释。因此,“两宽一高”地震采集技术虽然是高精度成像的重要保证,但是要实现该技术的工业化应用,还面临着巨大的挑战。
近年来发展起来的压缩感知理论[1-2],为“两宽一高”采集技术的工业化应用难题提供了解决思路。压缩感知理论指出,在信号是可压缩的或者在某个变换域是稀疏的前提下,可采用随机非规则采样的方式将信号由高维空间投影至低维空间,之后通过求解一个稀疏约束的优化问题重构原始信号。在压缩感知理论中,核心思想是将信号的采样以及压缩同时进行,信号采集时采样点数远小于Nyquist定理所要求的采样点数,因而使得采样成本大大降低。在地震勘探中,可通过设计随机非规则观测系统(炮点及检波点均少于Nyquist定理所要求的数量)有效地避开河流、村庄等障碍物,而后通过重建算法恢复完整的地震波场。因此将压缩感知理论运用到地震勘探中,可有效解决“两宽一高”采集技术所面临的难题,具有广阔的应用前景。
目前,压缩感知理论在地震数据去噪、地震数据重建以及反演等方面都有广泛的应用[3-8],但是将其应用于地震数据采集方面还处于初步研究阶段。HENNENFENT等[9]提出将抖动随机采样应用于地震数据采集。不同于完全随机采样,抖动随机采样在保持随机采样性质的同时,能够使采样点更加均匀分布,并且有利于控制采样点之间的距离,从而为后续的地震数据重建算法提供更有利的条件。MILTON[10]讨论了随机采样思想在地震观测系统设计中的应用,指出随机采样可以有效提高地震数据采集效率以及降低采集成本。MOSHER等[11-12]分别于2012年和2014年提出并完善了一种在观测系统设计中基于约束条件的更优选择激发点和接收点位置的非均匀采样方法。
基于压缩感知的地震采集技术,获得的数据需要利用一定的技术进行重建[13-14]。HENNENFENT等[9]于2008年提出通过抖动欠采样进行地震数据采集,并基于曲波变换进行数据重建;LI等[15]于2012年提出基于插值压缩感知(interpolated compressive sensing)的数据重建方法,设计了非均匀优化采样观测系统(non-uniform optimal sampling,NUOS),并进行了地震数据重建,分别在海上和陆上获得了良好的试验效果;国内学者对于基于压缩感知的地震数据重建也进行了一系列的研究。孔丽云等[16]讨论了压缩感知理论在地震数据重建中的应用,并指出曲波变换相较于傅里叶变换更具有优势。ZHANG等[17]在傅里叶域中利用迭代凸集投影算法(POCS)进行缺失地震数据重建。本文通过降低感知矩阵的最大互相关值,进行非规则观测系统的优化设计,然后通过L0正则化和L1正则化混合迭代的方法进行欠定采样矩阵的求解,完成地震数据的重建。
1 压缩感知基本理论
压缩感知的基本思想是当信号是稀疏的或者具有稀疏表达时,可以利用远少于Nyquist所要求的采样数量的线性、非自适应的测量值无失真的重建。压缩感知理论的核心思想是将压缩与采样合并进行,其优点是信号的投影测量数据量远远小于基于Nyquist定理的传统采样方法所获得的测量数据量,从而在数据采集时节省大量成本。但与此同时,必须采用适当的重构算法恢复原始信号。
已知一个测量矩阵Φ∈RM×N(M≪N)以及某未知信号x∈RN在该测量矩阵下的线性测量值y∈RM:
(1)
现在需考虑由测量值y重构恢复原始信号x。由于M≪N,因此问题是一个欠定问题,有无穷多个解,即很难进行原始信号的重构恢复。但是如果信号x是稀疏的,即x=Ψθ,通过求解原始信号的稀疏系数进而重构恢复原始信号。测量过程可写为:
(2)
其中,A=ΦΨ为M×N的矩阵,称为感知矩阵。此时,如果矩阵A满足约束等距性质,可以首先通过求解L0范数约束优化问题:
(3)
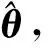
(4)
然而求解L0范数约束最优化问题是一个NP-hard问题,几乎不可能求解。CANDES等[2]通过证明指出在一定条件下L0范数约束优化问题与L1范数约束优化问题是等价的,此处的条件就是有限等距性(RIP)条件以及零空间性质。因此,L0范数约束优化问题可由下述L1范数约束优化问题代替,即:
(5)
2 基于压缩感知的重建方法
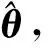
优化问题可通过硬阈值迭代算法进行求解,但是收敛速度慢且不稳定,并且需要信号的稀疏度信息。考虑到软阈值算法能快速确定解的支撑集,本文在进行硬阈值迭代算法之前,首先利用软阈值迭代获取信号的稀疏度信息,并为下一步迭代获取好的迭代初值,而后再进行硬阈值迭代算法求解优化问题。具体算法流程如下。
1) 初始化:x=0,k=1。
2) 执行软阈值迭代算法,获取信号的稀疏度信息,并为下一步迭代提供初值,即:
(6)
其中,Hs为软阈值函数,即:
(7)
3) 执行硬阈值迭代算法:
(8)
其中,HM为保留xn+1中最大的M项。
4) 满足迭代停止条件则停止迭代,否则k=k+1,返回第3)步。
3 模型数据测试
本文采用Marmousi模型验证上述重构算法的有效性。首先利用基于压缩感知的非均匀观测系统设计方法指导数据采集,而后进行数据的重建恢复。图1为Marmousi的速度模型,从图中可以看出,该模型中间有着非常复杂的高陡构造。
图2a为原始单炮数据,总道数为1181道,道间距为10m;图2b为利用65%的道数进行非规则设计后获取的不完整地震记录,图2c为使用本文算法恢复的地震记录。对比重构地震记录(图2c)与原始记录(图2a)可以看出,两者同相轴清晰,连续性好,振幅一致性准确,重构误差小。

图1 Marmousi速度模型
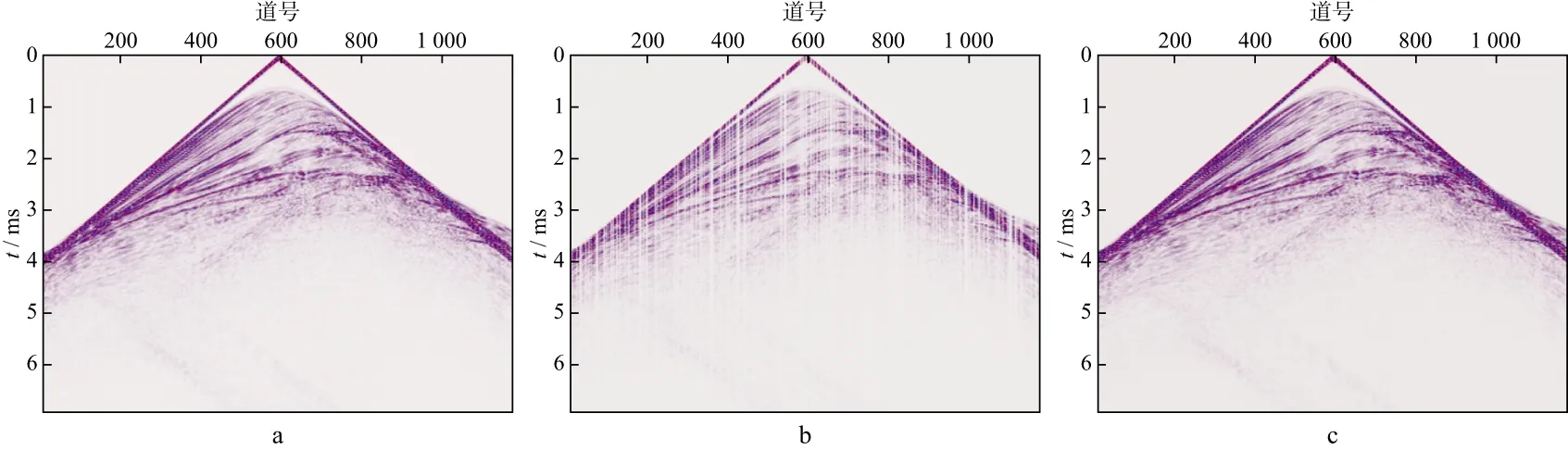
图2 理论模型地震记录重建结果的对比a 原始地震记录; b 随机缺失的地震记录; c 重建结果
图3是该测试数据记录响应的频谱。原始地震数据频谱(图3a)和重构地震数据频谱(图3c)可以看出,两者之间的频谱非常相近,误差很小,进一步表明了本文算法的数据重构的良好效果。以上均表明,通过基于压缩感知理论的重构模型,缺失的地震数据可以得到很好的恢复。
为了进一步验证重建效果,本文将原始数据与重建数据进行偏移成像,图4为对原始所有炮数据进行偏移而得到偏移剖面,图5为重建之后的数据进行偏移得到的偏移剖面。可以看出,经过重建之后,获得了高质量的偏移剖面。相较于原始数据偏移剖面,两者之间几乎没有差异,因此可以证明本文提出的算法具有良好的重建效果。

图3 与图1对应的地震记录的频率-波数谱a 来自原始地震记录; b 来自随机缺失的地震记录; c 来自重建结果
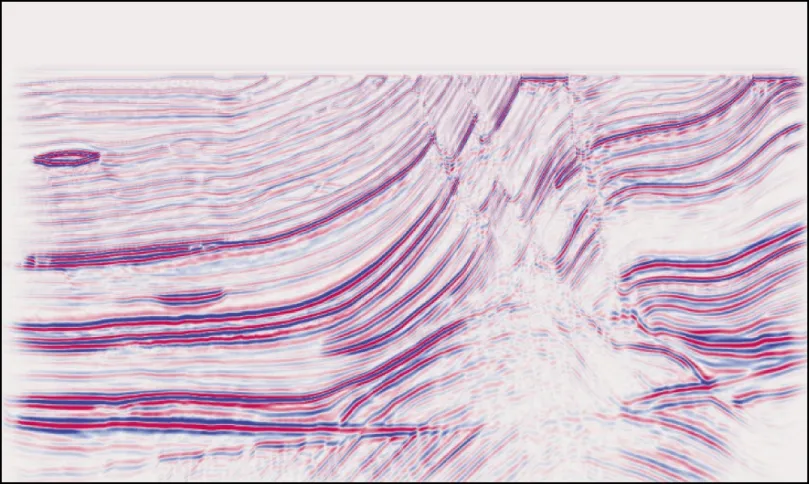
图4 原始数据偏移剖面

图5 重建数据偏移剖面
4 实际数据应用
为了验证压缩感知理论在实际地震勘探中的效果。在TFT地区进行了基于压缩感知的非规则观测系统设计(如图6所示),所选工区范围为14km×8km,检波点布设到整个工区范围,炮点区域为10km×2km。实际采集共部署炮点1760个,铺设33条常规检波器线,每条检波线365道。为了便于参照,增加了一条单点高密度检波线,2880道接收,道距5m。数据采集完成后,首先对非规则采集数据进行重建,重建的目标网格为42条接收线,线距180m,每条线465道,道间距15m。重建完成后,将本区域常规采集数据、基于压缩感知采集重建数据和高密度采集数据进行偏移成像的对比。图7a为常规采集数据偏移剖面,图7b为基于压缩感知采集数据偏移剖面,图7c为高密度采集数据偏移剖面,从图中可以看出,通过重建可使压缩感知采集数据达到了高密度采集数据的效果,比常规采集数据偏移剖面在分辨率和信噪比上都有很大的优势,且偏移剖面细节更加丰富。在小规模的测试试验中,本文的方法就节约了大量的固定投入和采集施工成本。
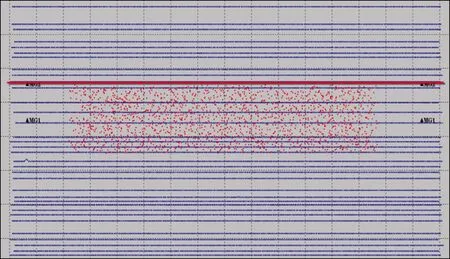
图6 优化设计的非规则观测系统(图中红点表示炮点位置,蓝点表示检波点位置)
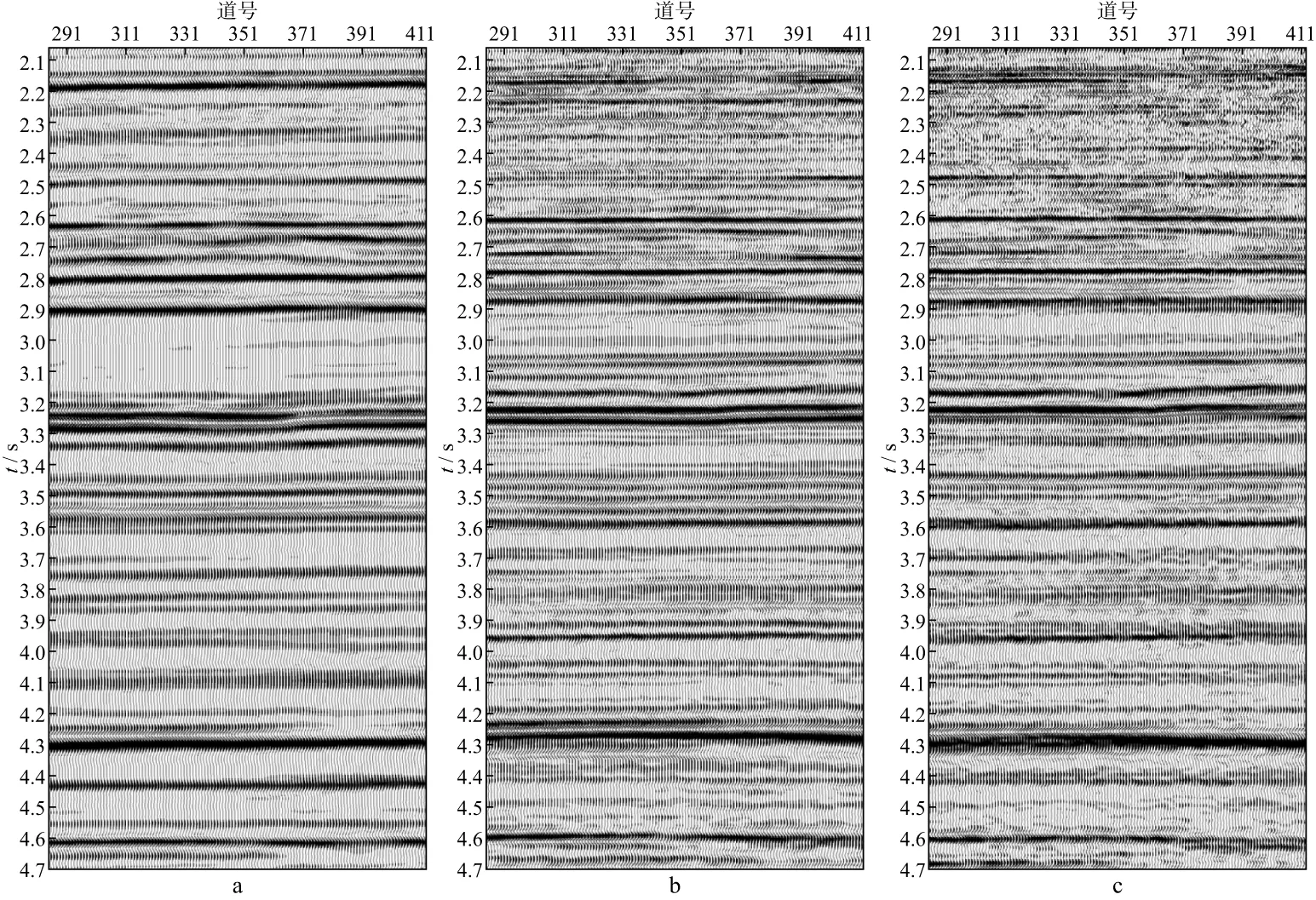
图7 偏移剖面对比a 常规采集偏移剖面; b 压缩感知采集偏移剖面; c 高密度采集偏移剖面
具体而言,综合采集成本可降低60%,而采集效率可提高6倍。在这样小的成本下,基于压缩感知的地震勘探方法还取得了更好的效果,所以该方法意义重大。
5 结论
基于压缩感知理论,本文提出利用软硬阈值混合迭代的方法进行地震数据的重建,获得了良好的效果。通过对实际工区基于压缩感知采集数据重建,获得了高质量的偏移剖面,信噪比与分辨率与高密度采样数据偏移剖面大致相同,明显优于常规采集数据偏移剖面。目前随着地震勘探开发的不断深入,勘探目标逐步由简单构造油气藏转变为岩性油气藏、断块油气藏以及火成岩油气藏等复杂构造油气藏,因而对地震勘探精度的要求不断提高。“两宽一高”(宽方位、宽频带、高密度)采集技术应用越来越广泛,该技术的应用可得到更加完整、更高精度的地震波场信息,在解决复杂构造成像、精细刻画油气藏以及各向异性研究等方面具有明显优势。但“两宽一高”采集时间及采集成本急剧提升。基于压缩感知的地震资料采集可以在较低的平均采样率下通过重建算法获得高精度的地震数据,从而有效降低地震数据采集的成本。对“两宽一高”地震勘探具有重要意义。
——工程地质勘察中,一种做交叉剖面的新方法

