Wallis和MASK匀光算法处理无人机影像比较研究

陈永星

(郑州市规划勘测设计研究院，郑州 450000)

0 引言

遥感影像获取过程中，由于摄影角度、大气效应、太阳光照、摄影时间长短、影像成像方式、曝光差异等多种因素的干扰，导致影像内部和影像之间出现亮度分布不均和色彩差异，影响影像质量和人眼目视判读，也影响遥感影像的后续应用[1]。随着无人机航摄的广泛应用，无人机影像的不均匀光照现象影响着无人机航摄的应用推广，因此，为了获取高质量的无人机航摄图像，必须对无人机影像进行匀光处理。

单幅影像的色彩一致性处理主要有两种方法：一是模拟光照法，即通过建立数学模型来模拟亮度分布，针对影像中亮度过暗或过亮的区域进行补偿。文献[2]给出了国外软件ERDAS Imagina 8.5提供的4种模拟光照模型；文献[3]中提出一种自适应模板算法进行匀光处理，但无法模拟影像不规则的亮度区域的亮度变化。另外一种是基于低通滤波器的自动匀光法。文献[2]提出了基于MASK原理的差值匀光法；文献[4]中先将原始影像按房屋和植被进行图像分割再分别进行低通滤波，最终合成背景影像；文献[5]中用小波分解保留低频系数，再小波重构得到背景影像；文献[6]中利用小波变换后不同子带图像上的频率特点，采用归一化方法生成背景影像；文献[7]中将小波系数进行自适应拉伸来模拟亮度分布；文献[8]中提出的基于非线性的MASK匀光处理算法，能够解决传统MASK算法中细节易损失的缺点。另外，还有基于Wallis滤波器的方法：文献[9]中指出，Wallis变换能够在增强局部反差的同时抑制噪声，起到色彩均衡的作用；文献[10]中提出将Wallis变换应用到基于小波变换的影像融合中，较好地把携带细节信号的小波分量分离出来；文献[11]中提出的一种基于Wallis滤波器的影像匀光算法，是通过对影像的合理分块自动统计标准均值和方差的反差一致性匀光处理算法；文献[11]中为了解决边缘扩张、灰度过饱和等问题，在此基础上提出了一种改进的自适应Wallis滤波算法；文献[12]还介绍了针对图像处理的Retinex法，Forsyth色域映射等方法。

遗憾的是，现有理论均针对传统的数字射影像图(DOM)匀光进行了探讨分析，但对无人机影像的匀光处理还鲜有研究。

论文分析了单幅影像Wallis匀光方法和MASK匀光方法在无人机影像匀光处理中的应用。采用Wallis匀光方法对无人机影像进行分块处理，通过Wallis滤波器使每块影像都具有大致相同的均值与方差，从而实现整幅图像的匀光。在MASK匀光方法中，探讨截止频率与对比度拉伸参数对图像的影响，从而得到最佳的匀光方案。最后，对这两种不同的算法得到的结果影像进行定量分析，实验表明，无论在定性和定量上，MASK匀光法的处理效果均较好。

1 分块处理的Wallis匀光法

Wallis是一种特殊的线性滤波器，通过局部变换，计算出不同影像整体的均值与方差，再利用Wallis滤波器使图像之间的均值与方差趋于一致，从而实现匀光。目前已广泛运用到图像处理领域。Wallis滤波器的一般形式如式(1)：

(1)

式中:g(x，y)为原始影像灰度值；f(x，y)为Wallis滤波之后的影像灰度值；mg为原始影像的灰度均值；mf为滤波后影像的灰度均值；sg为原始影像的局部灰度方差；sf为滤波后影像的灰度均值；c∈[0，1]为影像方差拓展常数；b∈[0，1]为影像亮度系数。当b无限接近于1时，影像均值趋向于mf；当b无限接近于0时，影像均值趋向于mg。所以，为了尽量保持原始影像的均值，应当设置较小的b值。

论文针对无人机单幅影像，提出了分块处理的Wallis匀光算法。首先，将原始无人机影像进行分块，分别求取每块影像的均值与方差；然后，选取所有分块影像中光照分布最均匀、均值最高的影像块作为基准影像，记录该块影像的均值与方差，将其运用到整块影像。这种分块算法的实现步骤如下所示：

1)将原始影像分成不重叠的若干块，分块多少可以依据影像的实际来定，计算每块影像的均值与方差。分块影像的均值公式如下：

(2)

分块影像的方差公式如下：

(3)

2)自动选取基准块影像。由于光照条件不同导致不同地区的亮度分布不同，所以灰度均值是选取基准块影像的标准。选取均值最大的影像块代表了光照条件最好，分布最均匀的部分，将其自动作为滤波用的标准方差。

影像的均值为mf=max(mgi)(i代表分块数)，

影像的方差为

(4)

3)对原始影像进行Wallis滤波处理。

2 MASK匀光法

MASK匀光法又称模糊正像匀光法，借鉴传统光学相片的晒印原理演变而来。该方法使用一张模糊的透明正片作为遮光板，将模糊透明正片和负片按轮廓线叠加在一起进行晒像，得到一张反差较小而密度比较均匀的相片，然后用硬性相纸晒印，增强整张相片的总体反差，最终得到晒印的光学相片。

对于存在不均匀光照的数字航摄影像采用下面的数学模型进行说明：

I′(x，y)=I(x，y)+B(x，y)，

(5)

式中：I′(x，y)代表需要匀光处理的原始影像；I(x，y)代表理想的光照均匀的相片；B(x，y)表示反映亮度分布的背景影像。由式(5)可知，影像之所以存在不均匀现象，是由于背景影像的不均匀导致的，如果能够合理地提取出背景影像，再将它与原始影像做减运算，就可以得到光照均匀的影像[13]。该公式还有另外一个形式：

Iout=Iin-Iblur+offset，

(6)

式中offset代表灰度偏移量，它表示处理后影像的平均亮度。通常用整幅影像的平均亮度表示，原始影像与背景影像的相减结果再加上偏移量，使得结果影像的灰度值处于合理亮度范围之内。

如何获取背景影像是MASK匀光算法中的关键步骤，一般是将原始影像进行快速傅里叶变换(FFT)，从时域转换到频域后经低通滤波得到，因此，选取合适的滤波器至关重要。目前，常用的频率域低通滤波器有理想低通滤波器、Butterworth低通滤波器和高斯低通滤波器等。目前存在的问题是低通滤波器是带通滤波器，需要不断地实验从而得到最合适的带宽，具有极大的不确定性，因此，选取合适的带宽对MASK匀光法是一个难题。

将原始影像与得到的背景影像做减运算，得到的影像会使得整体亮度的反差较小，有时不能很好地反映出图像的整体信息。为了突出图像的细节反差，解读出更多的图像信息，就需要对匀光处理后的结果图像进行拉伸处理。

王密与潘俊给出了一种拉伸模型[2]：

(7)

式中value为对比度拉伸参数，其取值范围为(-127，127)。存在两种特殊情况，如果处理后影像的值小于0，那么就把它定值为0，同样，如果大于255，那就定值为255。

3 实验分析

论文实验数据为某区域无人机航摄影像，图像特点是左上角偏亮，其余大片林地，存在阴影，整体偏暗，分辨率为1 024×1 024像素。为了验证上述方法对无人机影像的有效性，本次实验分别编写了分块处理的Wallis匀光算法和MASK匀光算法，对同一幅影像进行了实验，并进行质量评价。

3.1 分块处理的Wallis匀光法实验

原始实验数据如下，设置分块为4×4，、8×8、16×16 3种形式。

(a)原始影像

(b)分块数4×4

(c)分块数8×8

(d)分块数16×16

由图1可以看出，影像在4×4时匀光效果最好，整体亮度得到了提升的同时影像的整体色调也比较一致。

对分块为4×4的图像进行分析，由表1可知，经过Wallis滤波后，与原始影像的均值与方差相差较大，但是3通道之间相差不大，理论上实现了匀光，但是匀光的效果不理想，原始影像的整体色调偏暗，当分的块数变多时，就会使影像变得过亮，所以，该算法有一个弊端，当亮度过亮或者亮度过暗的面积超过一半时，如果不能合适地分块，自动选取出的基准影像就不会具有代表性，这样，影像的整体色调会发生巨大变化，且影像匀光结果中块与块之间存在边界，如何解决“块效应”还有待研究。

表1 匀光前后影像信息比较(分块为4×4)

3.2 MASK匀光法实验

目前有3种常见的滤波器：理想低通滤波器、Butterworth低通滤波器和高斯低通滤波器，效果较好的是高斯低通滤波器[2]，本文实验选取高斯低通滤波器，并通过对比实验选出最合适的截止频率和对比度拉伸参数。

3.2.1 不同截止频率的选取

选取合适的截止频率对MASK匀光法至关重要，目前还没有能够自动选取滤波器尺寸的方法，同时设置高斯低通滤波器和对比度拉伸参数为20保持不变。由图2可以看出，截止频率为1和2时，图像整体偏亮，跟原始影像差别较大，截止频率为2到4时，效果较好，截止频率为10时，由于滤掉了过多的低频信息，导致边缘突出，影像整体的色调太暗，匀光效果较差。

(a)原始影像

(b)截止频率=1

(d)截止频率=3

(e)截止频率=4

(f)截止频率=10

3.2.2 不同对比度拉伸参数的设置

为了突出影像的细节纹理，需要设置合适的对比度拉伸参数，实验的参数区间为[-40，40]，同时设置高斯低通滤波器和截止频率为3保持不变。

由图3可知，当拉伸参数为负时，影像整体偏白，拉伸参数为正时，匀光效果较好，但参数太大时，如拉伸参数=40，细节纹理太突出，不符合实际情况，因此，参数选择应该在合理范围之内，经过目视判读，参数为20时效果最好。

(a)原始影像

(b)拉伸参数=0

(c)拉伸参数=-20

(d)拉伸参数=20

(e)拉伸参数=-40

(f)拉伸参数=40

3.2.3 最佳匀光方案

经过3组实验，对比选出高斯低通滤波器、截止频率为3和对比度拉伸参数为20作为MASK匀光法的最佳方案，并对原始图像进行实验。

(a)匀光处理前

(b)匀光处理后

图5为匀光前后的灰度直方图，可以清楚地看到影像的灰度变化范围变大，直方图的起伏比匀光前减小，匀光效果较理想，主观上和客观评价上都证实了MASK匀光法的可行性。

3.3 两种匀光法的对比

在取得了两种匀光影像后，为了定量分析匀光后的影像质量，本文从亮度均值、标准差、信息熵和平均梯度4个方面对影像的内部和整体进行了质量评价[14]。

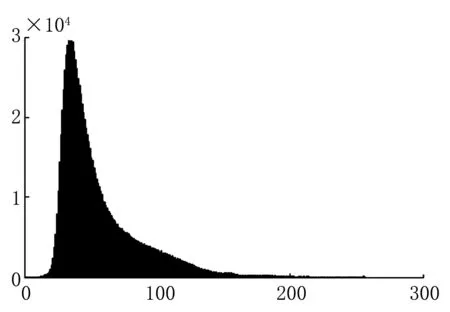
(a)匀光处理前

(b)匀光处理后图5 MASK匀光前与匀光后的灰度分布直方图

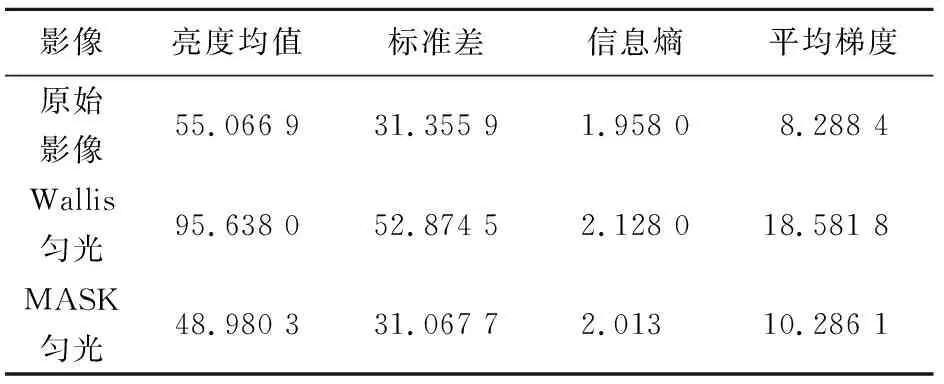
影像亮度均值标准差信息熵平均梯度原始影像55.066 931.355 91.958 08.288 4Wallis匀光95.638 052.874 52.128 018.581 8MASK匀光48.980 331.067 72.01310.286 1

从上表数据分析可知，Wallis匀光法处理后的影像亮度均值增加幅度最大，但是太亮不符合实际，MASK匀光法亮度均值减小，但与原始图像相差不大；MASK匀光法标准差基本不变，Wallis匀光法的标准差增幅很大，说明其对比度增大，这与目视判读结果是一致的；同时，两种算法的信息熵都有所增加，说明两种算法都丰富了影像的纹理信息；最后，两种算法的平均梯度增加，代表了影像的清晰度都得到提升。

综合以上目视观察和客观评价指标可以看出，两种算法都能对影像进行一定程度的匀光处理，但Wallis匀光法处理过的影像整体太亮，MASK匀光法的处理效果明显更好，在亮度均值和方差与原始影像大致保持一致的同时丰富了纹理信息，提高了影像质量，与目视判读的结论一致。

4 结语

为了对无人机影像进行匀光处理，首先进行了分块处理的Wallis的匀光法，理论上实现了匀光，但是目视上效果一般，主要原因是由于基准影像选取不合理导致，且存在“块效应”，所以还需要对其不断地完善。然后对经典的MASK匀光算法进行编程实现，针对影响MASK匀光结果的参数进行多组对比实验，找出最合适的匀光方案。对两种方法的结果影像进行质量评价，数据表明MASK匀光法效果更好，消除了影像亮度反差，使整体色调趋于一致，在亮度均值和方差与原始影像大致保持一致的同时丰富了纹理信息，提高了影像质量，效果更好。