一道初中数学联赛试题的题源及另解

☉安徽省南陵县春谷中学 傅昌平

☉安徽省南陵县春谷中学 邹守文

2014年全国初中数学联赛初二有这样一题：

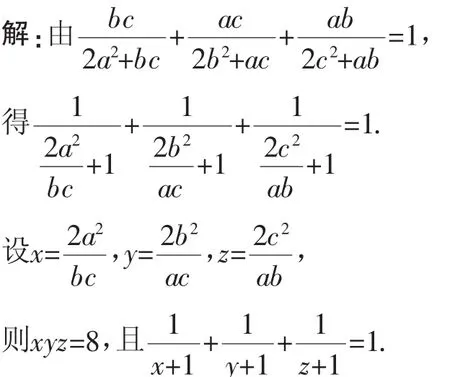
通分即得（y+1）（z+1）+（x+1）（z+1）+（x+1）（y+1）=（x+1）（y+1）（z+1），

展开后整理得xyz=x+y+z+2，所以x+y+z=6.

（a+b+c）［（a-b）2+（b-c）2+（c-a）2］=0.

又a，b，c不全相等，所以（a-b）2+（b-c）2+（c-a）2≠0，故a+b+c=0.

一、题源

所以原题等价于

题1是1995年江西景德镇市初中数学竞赛一题的逆向思考.

题2也曾作为1994年广西梧州初中数学竞赛试题.

由前面的变形，不难得到.

由原题的解题过程可以发现原题的本质.

题4是下面题目的逆命题：

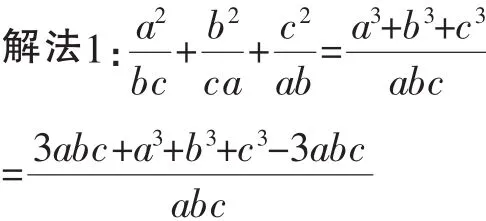
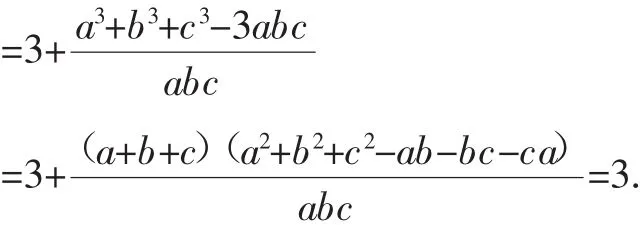
由于现在的初中教材已经删除了立方和公式，学生对于公式a3+b3+c3-3abc=（a+b+c）（a2+b2+c2-ab-bc-ca）不太熟悉或者根本不了解，怎么办？

通过变形，有

也可以这样变形：

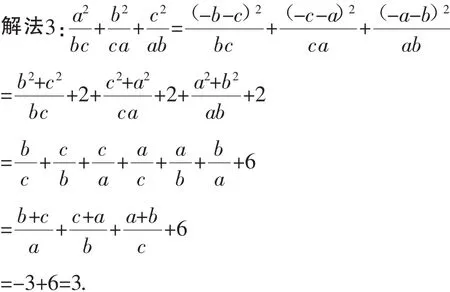
对题6的一个隐含条件题进行变式，有下题：

题7（2007年全国初中数学竞赛试题）已知三个关于x的一元二次方程ax2+bx+c=0，bx2+cx+a=0，cx2+ax+b=0恰有一个公共实数根，则的值为（ ）.

A.0 B.1 C.2 D.3

解：设x0是它们的一个公共实数根，则

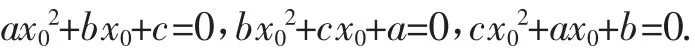
把上面三个式子相加，并整理得

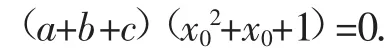
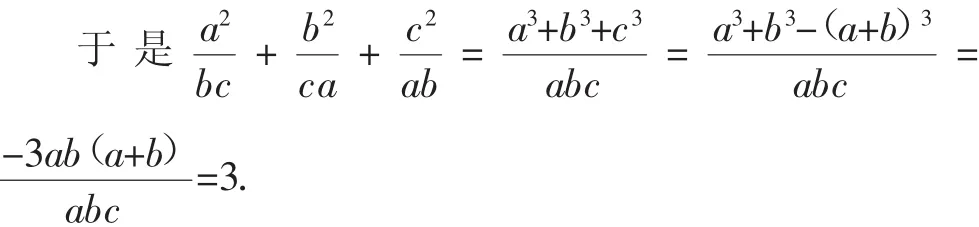
二、原题另解

即（2+y）（2+z）+（2+z）（2+x）+（2+x）（2+y）=（2+x）（2+y）（2+z），

以下同原题解答过程.

点评：另解1和原题的解如出一辙，可以看作是“姊妹”解法.但这里的变形技巧性更强.

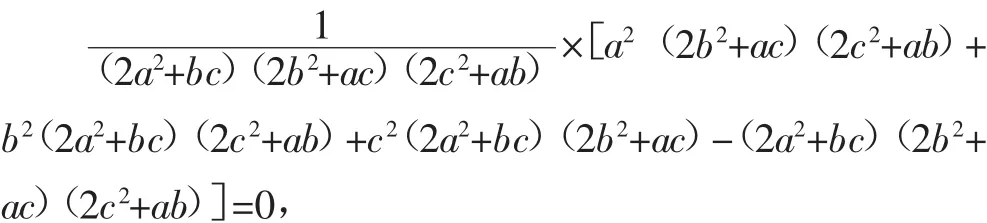
即a2（2b2+ac）（2c2+ab）+b2（2a2+bc）（2c2+ab）+c2（2a2+bc）（2b2+ac）-（2a2+bc）（2b2+ac）（2c2+ab）=0，

化简得3a2b2c2-abc（a3+b3+c3）=0.

于是有a3+b3+c3=3abc.

以下同原题解答过程.

点评：另解2尽管很“暴力”，但却是一种基本的思考问题的方法，很多学生由于运算的“暴力”而中途放弃，显得有点可惜.采用这种“暴力”运算的方法完全类似的可以证明题2.这样我们就可以找到两题的统一解法.