基于新型自适应遗传算法的混合可靠性优化模型

安海，阎朝一，孙鹏，尹瑰巧

哈尔滨工程大学 航天与建筑工程学院，哈尔滨 150001

遗传算法(Genetic Algorithm，GA)是由Holland[1]创立的一种模仿生物自然进化的优化算法。能够根据种群中个体适应度大小作为评判标准，利用类似于遗传学中的遗传算子对个体进行选择、交叉和变异，优胜劣汰从而逐代产生适应度更高的种群，在达到标准的末代种群中选择最优个体通过解码，即得到所求解问题的近似最优解。

标准遗传算法(Standard Genetic Algorithm，SGA)存在着诸如全局搜索能力差、收敛速度慢、对于不同问题要单独设置固定的交叉和变异概率以及难以解决复杂的优化问题等缺点。针对上述问题，人们已经提出许多改进方法。Moon和Linninger[2]应用了小生境技术来定位多模态优化问题中的所有解。Paszkowicz[3]将动态罚函数应用在遗传算法中。Hwang和He[4]将遗传算法与模拟退火相结合，使得全局搜索能力显着提高。

除了这些方法之外，Srinivas和Patnaik[5]提出的交叉率和变异率能进行线性的自适应调整的自适应遗传算法(Adaptive Genetic Algorithm，AGA)，被大量文献证明能够提升遗传算法的性能。然而，AGA也存在着诸如稳定性差和容易陷入局部最优解等问题。

针对以上问题，国内外许多学者从不同角度对其进行了改进，王小平[6]和任子武[7]等针对交叉和变异算子对其进行了线性型改进，使群体中最大适应度的个体交叉率和变异率不为零，使优良个体不处于停滞状态，从而使算法跳出局部最优解。石山等[8]结合余弦函数对交叉和变异算子进行了非线性调整，对接近最优值的个体采用较大的交叉、变异率，提高了搜索速度，对接近最优值的个体采用较小的交叉、变异率，保证不收敛于局部最优解。邝航宇[9]、Li[10]和张玉萍[11]等结合神经网络sigmod函数对交叉和变异算子进行了非线性型改进，使得算法在群体平均适应度和最佳适应度相差较大时，也能保持更快的收敛速度并且不收敛于局部最优解。除此之外， Ye等[12]提出了种群扰动方法来避免局部最优解。陈超[13]引进了相似系数来刻画当前一代种群个体之间的相似程度，并与Logistic函数结合对算法进行了改进，提高了算法的稳定性。José-Revuelta[14]引入个体适应度的信息熵概念，使得交叉概率和变异概率由信息熵决定，从而使种群规模降低，减小工作量，提高算法速度。Bingul[15]提出了动态适应度函数以解决动态环境下的多目标问题。

本文针对截尾随机-模糊-区间3种变量同时存在情况下的混合可靠性模型的优化问题，提出了一种针对交叉算子和变异算子形式调整的新型自适应遗传算法。概率与非概率混合可靠性模型[16-21]具有高维、非凸性、非线性、离散性的特点，针对该类模型的优化问题，优化过程中种群个体情况较为复杂，个体间的平均适应度与最佳适应度的差值较大，用现有的自适应遗传算法进行求解，容易陷入局部最优解中。本文结合Logistic函数和余弦函数，对交叉、变异算子曲线进行非线性化处理，使得在种群演化过程中最佳个体能够得到更好的保留，提高了全局搜索能力、收敛速度和精确度，有效地跳出局部收敛，避免早熟现象发生。并基于新型自适应遗传算法和混合可靠性模型，提出以混合可靠性指标作为优化约束条件的混合可靠性优化模型，以某型飞机同步器系统的优化设计为算例，验证了该模型的有效性。

1 自适应遗传算法

1.1 传统的自适应遗传算法

Srinivas和Patnaik[5]提出的AGA的交叉算子和变异算子为

(1)

(2)

式中：Pc为交叉算子；Pm为变异算子；fmax为种群的最大适应度值；favg为种群的平均适应度值；f′为参与交叉两个个体中较大的适应度值；f为变异个体的适应度值；k1、k2、k3和k4取[0,1]区间内的值。

此种动态调整Pm与Pc的方法，在群体进行进化的后期是比较适用的，然而对于尚处于进化初期阶段的种群是不利的。因为种群中较为优良的个体在种群进化初期基本没什么改变，但是这时得到的最优个体并不一定是原问题的全局最优结果。因此，这种动态调整方法很容易导致种群进化进入局部最优，最后得到的优化结果也不是最优解。

针对上述存在的问题，文献[6]给出了AGA的线性改进算法LAGA，对这种动态调整方法做出进一步的改进。LAGA中使种群中适应度为最大适应度值个体的交叉率和变异率取值大于0，把他们的值适当增大到Pcmin和Pmmin。这种调整方法能够保证种群中当代的优良个体不被破坏，使遗传操作能够持续进行，最终获得对原问题的最优结果。

经过上述的进一步改进，Pc、Pm的表达式可修改为

Pc=

(3)

Pm=

(4)

式中：Pc max为最大的交叉率;Pc min为最小的交叉率；Pm max为最大的变异率;Pm min为最小的变异率。

由式(3)和式(4)可知，当种群中有更多个体的适应度接近平均适应值时，这些个体具有相同的模式，并占据了种群中的大多数。 当平均适应度接近种群的最大适应度值时，交叉概率和变异概率差别很大，导致大多数个体只有较低的交叉概率和变异概率，进化变得停滞不前。另一方面，它也难以淘汰局部最优个体，使算法的全局搜索能力变差。

1.2 余弦改进型的自适应遗传算法

为防止交叉率和突变率选择不当，导致算法过早收敛或收敛速度慢的现象。交叉算子和变异算子的选择不能简单地随着适应度线性变化，而应该进行非线性调整。其中比较典型的改进算法是文献[8]提出的余弦改进型的自适应遗传算法(CAGA)，构造的自适应遗传算子为

(5)

Pm=

(6)

CAGA相对LAGA而言，适应度处在区间[favg,(favg+fmax)/2]的个体的交叉率和变异率有所提高。 由于适应度处于favg附近的个体并不理想，做出这种改进，可以使这类个体得到进化。 CAGA降低了适应度处在区间[(favg+fmax)/2,fmax]内个体的交叉率和变异率，这有助于种群中的优良个体得以保留。

CAGA中，因为Pc min和Pc max取值范围均为[0,1]，所以它们的差值|ΔPc|≤1，同样，Pm min和Pm max之间的差值|ΔPm|≤1。但是对于不同的种群来说，favg和fmax之间的差值|Δf|差别会很大。当|Δf|较大时，CAGA的自适应调整曲线如图1所示。

如图1所示，当favg和fmax之间的差值|Δf|较小时，CAGA相较于LAGA的优势明显，可以提高种群中早期个体突变率和交叉率，同时是种群中后期的优良个体得到保留；但是当favg和fmax之间的差值|Δf|较大时，CAGA的表现与LAGA基本相当，失去了非线性改进的优势。

1.3 构造新型自适应遗传算法

针对上述存在的问题，文献[8-9]相关方法，对这种动态调整方法做出进一步的改进，基于Logistic函数和余弦函数，改进了一般自适应算法的交叉算子和变异算子，构造了一种新的自适应遗传算子，从而提出一种新型自适应遗传算法(New Adaptive Genetic Algorithm，NAGA)。

为了避免在算法演化过程中出现停滞现象，克服自适应调整曲线在favg和fmax相差较大时自适应调整曲线与LAGA相接近甚至部分重合，首先，应该让交叉算子和变异算子的函数在favg附近保持较高的值，并且进行缓慢地变化，从而大范围地使适应度处于favg附近的个体拥有较高的交叉率和变异率；其次，为了避免陷入局部收敛，应该让交叉算子和变异算子的函数在fmax附近保持不为0的较低的值，适应度处于fmax附近的个体拥有大于0的交叉率和变异率，从而让优良个体得以保留的同时不出现局部最优解。由以上可知，整个交叉算子和变异算子函数的曲线在种群演化的前期和后期保持平滑。

考虑到以上交叉率及变异率需满足的特点，现引入简化的Logistic函数，该函数的具有以下两个优良的性质，一是具有更平滑的底部和顶部，更加满足交叉率和变异率的要求，二是函数值域范围限定为[0,1]，能够更加方便地构造交叉算子和变异算子公式。

Logistic方程的积分形式为

(7)

式中:N为生物量、生长量或其他数量指标；t为时间序列；r为常数，为自然增长率或瞬时增长率；K为常数，称为环境负载力或容纳量；a为积分常数。式(7)即为S形Logistic累计分布曲线方程。

在式(7)的基础上，令K=1,a=0,r=1,N=φ(x),t=x，即得到简化的函数方程为

(8)

如图2所示，式(8)函数的顶部和底部和余弦函数相比更加的平滑。由文献[10]可知，φ(x)有以下性质：当x≥9.903 438时，φ(x)接近1；当x≤-9.903 438时，φ(x)接近0。

考虑非线性的调整方法，将φ(x)中的自变量x用式(5)中的余弦函数部分Acos[π(f′-favg)/(fmax-favg)]替换，其中由于f′的变化范围为区间[favg,fmax],Acos[π(f′-favg)/(fmax-favg)]在此区间的取值范围为[0,1]区间，由上述φ(x)的相关性质可得，要使φ(x)的值域范围在[0,1]，则设定A=9.903 438。构造的以个体适应度f′为自变量的Logistic函数和余弦函数的复合函数为

(9)

对式(9)关于f′求导，易知函数φ(f′)的导数在[favg,(favg+fmax)/2]∪[(favg+fmax)/2,fmax]区间的导数接近于0，说明该复合函数和单独的Logistic函数与余弦函数相比，在顶部和底部都更加的平滑，也能够表明由此复合函数构成的自适应遗传算子的性能更加优良。

最终可得交叉算子和变异算子的函数表达式分别为

Pc=

(10)

Pm=

(11)

式中:交叉算子Pc的取值范围是0.5～0.9，Pc max为最大的交叉率，取Pc区间范围内较大的值，Pc min为最小的交叉率，取Pc区间范围内较小的值；变异算子Pm的取值范围是0.01～0.1，Pm max为最大的变异率，取Pm区间范围内较大的值，Pm min为最小的变异率，取Pm区间范围内较小的值。

对应的交叉算子和变异算子的函数图像如图3所示。

由式(10)和式(11)可知，本算法可以根据平均适应度favg与最大适应度fmax之间的个体适应度，利用由Logistic函数和余弦函数组成的复合函数非线性地调整交叉率和变异率。由图3可得，当种群中的大部分个体具有相似的适应度，并且平均适应度接近最大适应度时，大部分个体的交叉率和变异率得以增加。同时，对于适应度在最大适应度值附近的个体，使它们的交叉率和变异率降低并且大于0，从而使优良个体得以保留，并使算法跳出局部最优解。

当求解最小优化问题时，自适应遗传算子的函数表达式为

(12)

(13)

对应的交叉算子和变异算子的函数图像如图4所示。

当求解最大优化问题中种群的favg和fmax相差较大时，LAGA、CAGA和NAGA交叉算子/变异算子的函数图像对比如图5所示。

与传统的自适应遗传算子调整方法相比较，这种调整方法能够更好地提高种群中适应度处于区间[favg,(favg+fmax)/2]的个体的交叉率和变异率，从而使自适应遗传算法的收敛速度更快；也在降低了种群中适应度处于区间[(favg+fmax)/2,fmax]的个体的交叉率和变异率的同时，使得个体交叉率和变异率大于0，从而使种群保留优良个体的同时不陷入局部最优解。并且，如图5可知，NAGA的图像更加地平滑，当favg和fmax之间的差值|Δf|较大时，NAGA的交叉/变异算子函数图像，无论|Δf|的值有多大变化，都不会出现与CAGA及LAGA接近甚至重合的现象。这样，对于求解种群中个体差异较大的复杂优化问题时，既能加快算法的收敛速度，又能够跳出局部最优解，提高了算法的精确度和稳定性。

1.4 计算验证

为验证算法的稳定性和收敛性，将SGA、LAGA及本文提出的NAGA进行比较，3种算法均采用二进制编码及经典的轮盘赌选择策略，下面通过求解最小优化问题的测试函数，验证NAGA算法的性能。

1.4.1 线性测试函数验证

1) 算例问题描述

设实际的目标函数为

f(x)=5x1+4x2+6x3

(14)

该目标函数的相应约束为

(15)

要求：求解目标函数f(x)的最小值。

2) 算例分析

分析算例问题的目标函数和相应约束，用经典的优化算法容易得到，目标函数f(x)在约束内的极小值为0，即fmin=0，此时x1=0,x2=0,x3=0。这是一个经典问题，下面通过SGA、LAGA和本文所提出的NAGA程序对该实际问题进行优化计算，可得出最后的优化结果。

3) 参数设定(如表1所示)

表1 线性测试函数下算法参数值的设定

4) 3种优化算法优化结果对比(如图6所示)

针对上述优化问题，用SGA得到的最佳适应度值为9.314 2，相应的最佳个体取值为x1=0.899 5,x2=0.546 9,x3=0.438 1，从优化结果看和实际结果有较大出入；用LAGA得到的最佳适应度值为0.488 5，相应的最佳个体取值为x1=0.051 7,x2=0.024 2,x3=0.022 2，其优化结果和实际的结果还是有一定的差距。而用NAGA得到的最佳适应度值为0.083 0，相应的最佳个体取值为x1=0.006 3,x2=0.008 2,x3=0.003 1，其优化结果和实际结果差别不大，在误差范围内。从上述结果的简单对比分析可知，NAGA在求解优化问题时得到的结果更精确。

由图6可知,SGA得出的结果和实际结果不符合，且陷入了局部最优。而且NAGA收敛性明显比SGA和LAGA的收敛性好，收敛速度更快，根据图6可知NAGA对于同样的问题在迭代60次时，优化结果已经趋近于实际结果。

1.4.2 非线性测试函数验证

1) 算例问题描述

设目标函数为

f(x,y)=x2+2y2-0.4cos(3πx)-

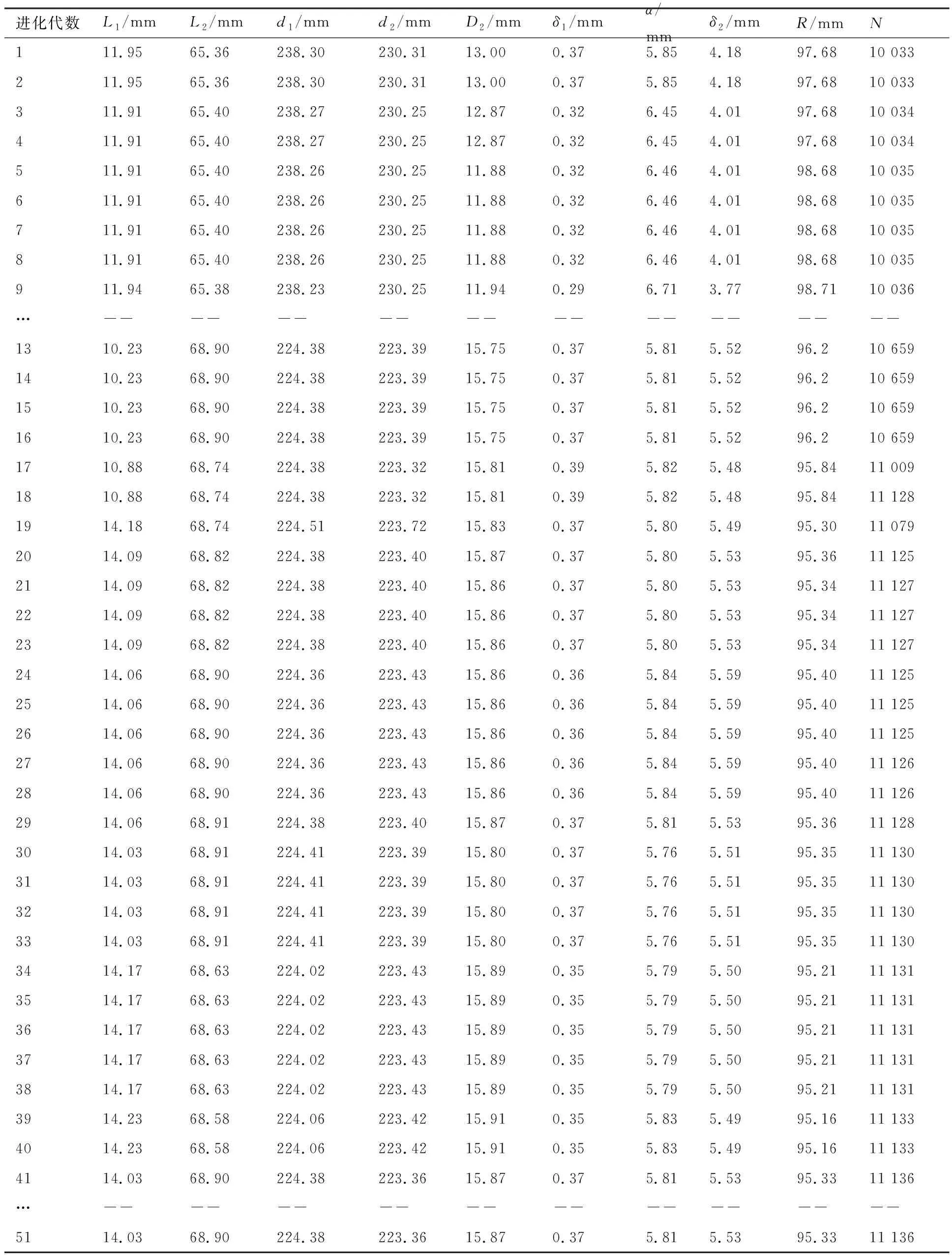
0.6cos(4πy) -10

(16)

要求：求解目标函数f(x,y)的最小值。

2) 算例分析

测试函数f(x,y)是一个多极小值函数，只有一个全局最小点(0,0)，此时函数的最小值为-1，每一个谷底都是一个局部最小点，因此优化过程中算法很容易在这些局部最小点形成局部收敛。该函数是检验遗传算法全局搜索性能的一个经典函数，函数图像如图7所示。

下面通过SGA、LAGA和NAGA程序对该实际问题进行优化计算，得出最后的优化结果。

3) 参数设定(如表2所示)

4) 3种优化算法优化结果对比(如图8所示)

由图8可知，用SGA得到的最佳适应度值为-0.428 0，相应的最佳个体取值为x=0.021 8,y=0.436 2；用LAGA得到的最佳适应度值为-0.520 1，相应的最佳个体取值为x=0.002 3,y=0.477 5；而用NAGA得到的最佳适应度值为-0.962 5，相应的最佳个体取值为x=-0.033 3,y=-0.018 6，其优化结果和实际的结果差别不大，在误差范围内。从上述结果的简单对比分析可知，SGA和LAGA陷入了局部最优。而NAGA收敛性明显比SGA和LAGA的收敛性好，收敛速度更快，在进化代数15代时，优化结果已经趋近于实际结果。

表2非线性测试函数下算法参数值的设定

Table2Algorithmparametervaluessettingofnonlinearfunctiontest

参数种群大小最大进化代数PcmaxPcmaxPmmaxPmmin值50300.850.50.10.02

2 基于NAGA的混合可靠性优化模型

2.1 截尾随机-模糊-区间变量混合可靠性模型

工程中往往是截尾随机变量、模糊变量与区间变量混合存在的。文献[18]应用经典的应力-强度模型来描述这一问题，此时可得其结构安全余量函数为

(17)

当强度R与应力S不相互干涉时，很显然此时的强度R始终大于应力S，那么结构的概率可靠度值应为1,此时可将截尾随机变量当作区间变量，即只用到其上下界，不考虑其内部分布。因为在不发生干涉时其内部分布信息是不会对可靠性度量结果产生影响的，因而可采用非概率指标可靠性指标η进行此时的可靠性度量，非概率指标可靠性指标η应用序列二次规划法求解。η的表达式为

(18)

式中:Δv′为从截尾随机变量转化来的标准区间向量；m为截尾随机变量的个数；n为区间变量的数量；δi为截尾随机变量在标准区间扩展空间中的第i个标准区间变量；δj为区间变量在标准区间扩展空间中的第j个标准区间变量。

当强度R和应力S相互干涉时，应用概率可靠性指标β来对结构此时所处的状态进行可靠性度量，可靠性指标β可用改进的一次二阶矩法求解。β的表达式为

(19)

综上所述，应用混合可靠性指标κ来对此时结构所处的状态进行可靠性度量:

(20)

2.2 优化步骤

1) 建立结构系统的优化设计模型

分析结构系统的各个变量类型并判定变量的取值范围，确定优化问题的目标函数表达式。确定结构系统的失效模式，并得出失效面方程，分析失效面方程中各个变量的类型并相应标准化。

基于本文提出的NAGA，并结合混合可靠性指标求解方法，给出一般情况下基于新型自适应遗传算法的混合可靠性优化设计模型：

(21)

式中:X为优化设计变量向量；f(X)为待优化的目标函数；κj为第j种失效面方程对应的系统可靠性指标；κj 0为第j种失效面方程对应的系统可靠性指标的设计值；gj(X,u,Δv)=0为第j种失效面方程；uR、uL分别为组合向量的上下限；Δv为标准化后的区间向量；XR、XL为优化设计变量的上下限。

2) 目标函数到适应度值函数转化

若目标函数为最小值问题

(22)

式中:cmax为一个比较大的数，近似可取f(x)的最大估计值。

若目标函数为最大值问题

(23)

式中:cmin近似可取为f(x)的最小估计值。

3) 初始种群的产生

根据所优化的问题选择种群规模n,随机产生初始化种群，采用十进制编码方法对各个变量进行编码。

4) 系统混合可靠性指标κ的求解

根据系统优化设计模型中的失效面方程，求解混合可靠性指标κ，分两种情况：

情况1当η>1时，根据文献[18]混合可靠性指标的定义，此时κ=η。把混合可靠性优化问题中的约束极限状态方程表示成式(18)所示。针对式(18)的可靠性指标表达形式，求得的非概率可靠性指标η即为混合可靠性指标κ的值。

情况2当η≤1时，需要求解可靠性指标β来表示结构系统的可靠程度，此时的混合可靠性指标κ=Φ(β)。对β的求解，需要将约束中的极限状态方程表示成式(19)所示，然后应用改进的一次二阶矩法对概率可靠性指标β求解。

5) 初始化种群中各个体适应度值的计算

按照式(22)或式(23)计算种群中个体的适应度值。

6) 用迭代终止条件对运行过程进行判断，若满足迭代终止条件，则停止迭代。迭代终止条件是最佳适应度值进化10代内变化幅度不超过10-5。

7) 寻找并记录最佳个体

在当代种群个体中寻找适应度值最大的那个个体作为最佳搜索个体，并记录保留到后代。

8) 运行选择算子程序

应用轮盘赌策略对种群中的个体进行选择，个体所占概率越大，越容易被选中到下一代中。具体选择方法如下：若种群规模为n，第i个个体适应度值为f(xi)，那么该个体被选择到下一代的概率为

(24)

9) 交叉和变异

根据式(10)和式(11)或式(12)和式(13)进行交叉和变异操作，其中Pc max=0.85,Pc min=0.5,Pm max=0.1,Pm min=0.02。

10) 针对交叉和变异后的个体，计算其最佳适应度值，同时剔除最差个体。若最佳适应度值不如父辈则被替代，记录最佳适应度值在种群中的位置。

11) 形成新的一代种群，然后返回至第4步继续。

根据上述过程可以得到基于NAGA的混合可靠性优化算法运行计算流程图,如图9所示。

3 基于NAGA的同步器系统可靠性优化设计

某型飞机变速箱同步器系统中的滑块磨损与同步器体锥面磨损是两个主要的失效模式，失效模式表达式中包含多种不确定变量。下面给出同步器系统的可靠性优化模型。

1) 同步器系统不确定参数类型确定

分析同步器系统各个设计参量，根据设计经验和实验模拟可以得到同步器参数的不确定性类型，如表3所示。

2) 同步器滑块可靠性优化模型

滑块磨损是同步器系统磨损中主要的失效形式，为了减少滑块磨损量，提高同步器寿命，提出了对滑块磨损的关键结构进行可靠性优化。滑块主要由拨叉带动，将力传递给拨叉环，从而进行换挡操作。因此进行优化的主要部件即滑块与拨叉环。

表3 同步器系统不确定参数Table 3 Indeterminate parameters of synchronizer system

图10为拨叉环与滑块的结构简图。图中:L1、L2分别为滑块的高和宽；D1=130 mm为滑块上端到轴心的距离，该距离由拨叉环与轴的相对位置确定；d1、d2分别为拨叉环的外、内圈的直径，外圈直径最大值为以不与拨叉产生干涉为准，其中内圈最小值由其内部的同步器体限制。因此同步器滑块可靠性优化模型的设计变量和约束条件如下：

① 设计变量

滑块高度：L1∈[5,20] mm；滑块宽度：L2∈[35,70] mm；拨叉环外圈直径：d1∈[220,258] mm； 拨叉环内圈直径：d2∈[220,258] mm。

② 约束条件

(25)

单次磨损量h1表示为[23]

(26)

(27)

式中：K为滑块磨损系数，该系数由仿真试验结果得到，由于试验拟合得到的数据存在一定离散性，因此其为区间变量，区间为[2.39×10-7,2.51×10-7];ρ=7.8×103kg/m3表示滑块密度；H=45～52 HRC，表示接触材料硬度，可取为区间变量[45,52] HRC;F为正压力，具有随机性，均值为μF=1 850 N，标准差为σF=79 N，截尾区间为[1 613, 2 087]N;L为相对滑动距离，L=2πωr·t=(πω(d1+d2)·t)/2(L求解表达式中，t为同步时间，t=1.3 s;ω为相对速度，ω=1 600 r/min;r为接触半径，r=(d1+d2)/4))；单个滑块接触面积A的求解表达式为

(28)

(29)

3) 同步器体锥面可靠性优化模型

为了减少同步器体磨损量，提高同步器寿命，提出了对同步器体锥面磨损的关键结构进行可靠性优化。在同步过程中，同步器体与主动齿轮的锥面接触摩擦，产生力矩迫使输入齿轮与输出轴速度同步，因此锥面处容易造成磨损。

(30)

D2为锥面宽度，其尺寸受主动齿轮的影响，

可以在范围内微调，R为锥面最小半径，其尺寸即要求主动齿轮内侧与输出轴齿轮啮合的内齿轮干涉，同时还要保证为内齿轮留有足够齿厚以保证啮合强度。

因此同步器滑块优化结果如下：

① 设计变量

锥面宽度：D2∈[10,20]； 锥面间隙：δ1∈[0.1,0.4]；锥面半锥角：α∈[5°,10°]；齿套与啮合齿的间隙：δ2∈[2,6]；锥面最小半径：R∈[90,100]。

② 约束条件如下

(31)

式中:ρ=7.8×103kg/m3为同步器体密度；t=1.3 s为同步时间;F为轴向换挡力，具有随机性，均值为μF=3 000 N，标准差为σF=30 N，截尾区间为[2 010, 3 090]N;υ0为相对转速，具有一定随机性，均值为μυ0=4.5 m/s，标准差为συ0=0.2 m/s，截尾区间为[3.9, 5.1] m/s。锥面面积S的计算过程如下：

由锥面宽度D2、锥面最小半径R和锥角α可知，锥面最大半径R1为

R1=R+D2tanα

(32)

可以求得锥面最大直径与锥面最小直径对应的圆锥母线长度分别为(将锥面展开后为扇形)

(33)

因此可以求得圆锥锥角β′为

β′=2πsinα

(34)

可以求得锥面面积为

(35)

s.t.

(36)

4) 同步器系统可靠性优化模型

综合同步器滑块与同步器体锥面的可靠性优化模型，得到同步器体系统的可靠性优化模型如下:

(37)

采用NAGA对式(37)的优化模型进行求解，算法控制参数如表4所示。其中迭代终止条件为：最佳适应度值在10次遗传代数内，变化不超过10-4。那么，经过51代的进化迭代得到最终优化结果统计如表5所示，图12为最佳适应值的迭代过程。

应用NAGA对混合可靠性优化模型进行求解，最终得到同步器系统的最优设计尺寸为L2=68.90 mm,L1=14.03 mm,d1=224.38 mm,d2=223.36 mm,D2=15.87 mm,δ1=0.37 mm,α=5.81°,δ2=5.53 mm,R=95.33 mm,N=fbest=11 136次。

表4 NAGA参数值设定

表5 NAGA优化结果Table 5 Optimization results of NAGA

注：表格中--符号表示数据与之前数据一样

4 结 论

1) 本文通过对交叉算子和变形算子线性改进型自适应遗传算法(LAGA)以及余弦改进型自适应遗传算法(CAGA)进行分析，指出了传统自适应遗传算法收敛性和稳定性不足的原因。结合Logistic函数与余弦函数对交叉算子和变形算子进行了非线性自适应调整，提出一种新型自适应遗传算法(NAGA)。通过求解最小优化问题的测试函数验证可知，新算法比常用的自适应算法具有收敛性好，收敛速度更快，稳定性高，能够很快跳出局部收敛的优点。

2) 针对实际工程中含有多种不同变量的机械可靠性优化问题，提出了基于新型自适应遗传算法(NAGA)的混合可靠性优化模型，并应用于同步器系统的可靠性优化问题中。通过算例，给出同步器含有截尾随机-模糊-区间3种变量同时存在的混合可靠性优化模型，并求解出优化结果，表明了该模型在工程实际中具有良好的应用性。

3) 新算法采用轮盘赌法进行种群选择，适应度函数的构造也采用了较为简单的方法，可能会导致最后的优化结果有一定的偏差。因此，对新型自适应遗传算法(NAGA)的适应度函数构造方法和种群选择的方法优化有待进一步深入研究。