考虑第一类两难区的黄灯信号时长优化

张亚平, 温 良，祁首铭，莫 琼

(哈尔滨工业大学 交通科学与工程学院，黑龙江 哈尔滨 150090)

0 引 言

交叉口是城市道路中发生车流冲突的主要区域，其中直行车流和左转车流是冲突产生的主要因素。为了减少车流冲突对交叉口交通的影响，保证交叉口行车安全，多数信号控制交叉口均采用设置左转专用相位的方式，从运行时间上分离冲突车流，同时配合专用车道，有效提高了交叉口的运行效率，减少了因为车流冲突发生交通事故的可能性。信号控制方式的引入特别是黄灯信号的应用，产生的两难区问题却成为诱发交叉口交通事故的潜在不安全因素。合理设置黄灯信号时长，对于消除第一类两难区，确保交叉口车辆运行安全至关重要。

目前，对于左转专用相位的黄灯信号时长设置，通常与直行相位相同。北京地区基本采用4 s，美国采用3～6 s，德国根据进口道限速值的不同，分别取3、4和5 s[1]。现有的黄灯信号时长计算模型中涉及到驾驶人决策行为的变量，例如行驶速度、加速度以及感知反应时间往往取定值[2]。运用这些模型计算出来的黄灯信号时长并不能与驾驶人的决策行为相适应，有可能会导致车辆陷入第一类两难区，增加交通事故发生的可能性。国内对于黄灯信号时长的研究不多，关于左转专用相位的黄灯信号时长研究更是少之又少。采用视频观测法对限速值为60 km/h的城市干道典型信号交叉口直行相位和左转专用相位黄灯期间进口道车辆进行观测，基于观测数据对直行相位和左转专用相位第一类两难区进行建模，研究黄灯期间车辆运行状态，以期为直行相位和左转专用相位黄灯信号时长优化设置提供理论依据。

1 数据采集

选取哈尔滨市学府路-保健路和学府路-学府东四道街两个十字信号交叉口作为视频观测点，其直行与左转相位黄灯信号时长均为3 s。观测点满足以下条件：交叉口限速值为60 km/h；进口道信号有左转专用相位和左转专用车道；进口道视距良好、无遮挡；进口道上游有人行天桥作为摄像机架设点。

在进口道上游天桥选择最佳位置，架设摄像机，记录目标车道交通流状态。视频观测如图1。为了避免天气等其他因素干扰观测结果，观测时间选定为天气晴朗工作日下午14:00—18:00，每个交叉口连续观测3个工作日。

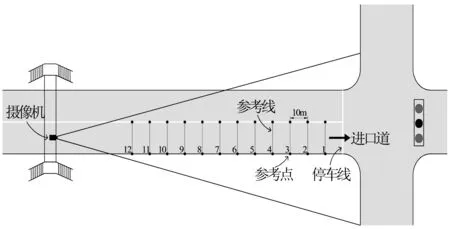
图1 视频观测示意Fig. 1 Video observation

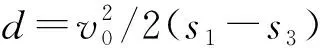
2 第一类两难区建模

对黄灯信号时长、行驶速度、周期时长与感知反应时间、制动减速度、行驶加速度分别做相关性检验后发现，只有行驶速度为显著因素。因此应用SPSS分析软件选择线性函数、对数函数、倒数函数、幂函数、S型函数、指数函数分别构建制动反应时间-行驶速度模型、制动减速度-行驶速度模型、行驶加速度-行驶速度模型。

根据文献资料显示，制动反应时间随黄灯启亮瞬间车辆与停车线之间距离增大而减小[4]。因此选择黄灯启亮时不同速度到达的车辆至停车线距离最小的47组直行首停车和29组左转首停车数据作为模型构建的数据。拟合结果如表1。

拟合结果表明：线性函数和指数函数分别可以较好地表征直行首停车和左转首停车制动反应时间与行驶速度之间的关系。拟合得到的模型与文献[4]研究结果感知反应时间随行驶速度增大而减小相一致。因此直行和左转制动反应时间-行驶速度模型可以分别表示为

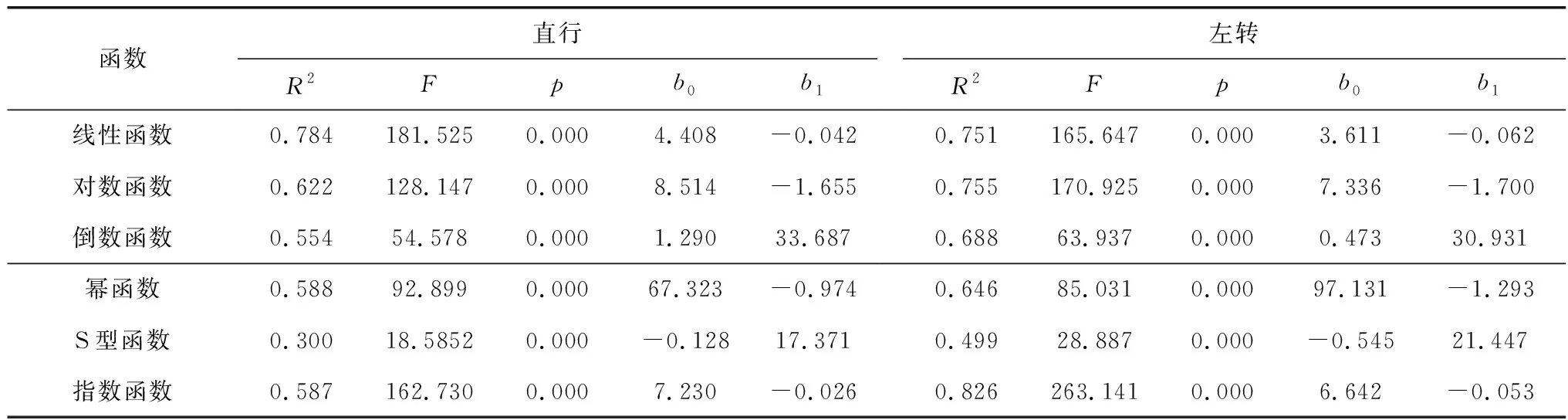
表1 制动反应时间-行驶速度模型拟合结果Table 1 Fitting results of braking response time and running speed model

δS=4.408-0.042V0

(1)

δL=6.642e-0.055 3V0

(2)

现有研究成果表明：制动减速度随黄灯启亮瞬间车辆与停车线之间距离增大而减小[5]。因此仅选择黄灯启亮时不同速度到达的车辆至停车线距离最小的65组直行和31组左转首停车数据作为模型构建的数据。拟合结果如表2。

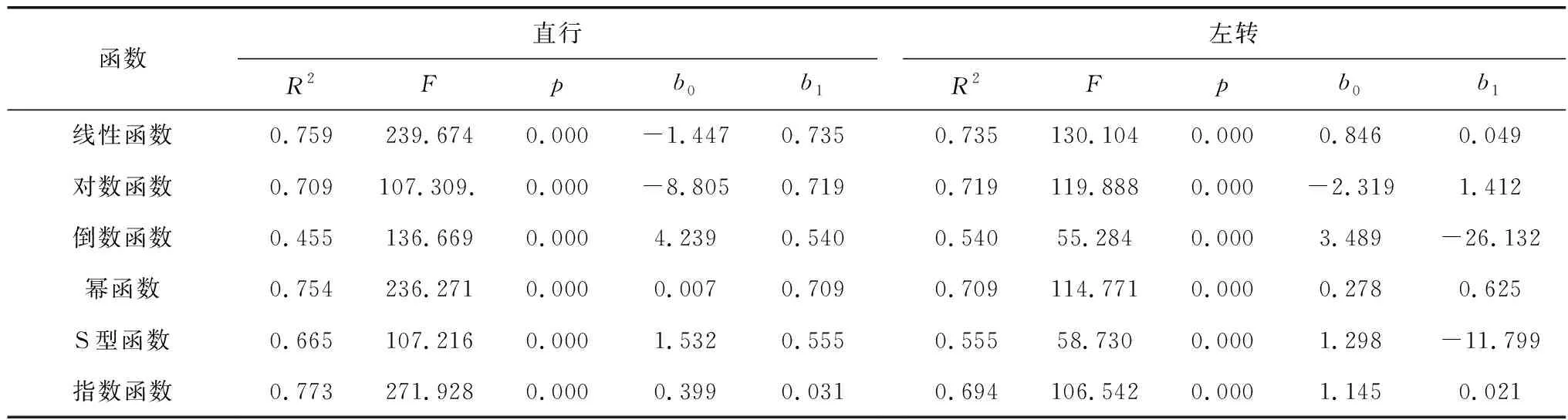
表2 制动减速度-行驶速度模型拟合结果Table 2 Fitting results of braking deceleration and running speed model

拟合结果表明：指数函数和线性函数分别可以较好地表征直行首停车和左转首停车制动减速度与行驶速度之间的关系。拟合得到的模型与文献[5]研究结果制动减速度随行驶速度增大而增大相一致。因此直行和左转制动减速度-行驶速度模型可以分别表示为

dS=0.399e0.031V0

(3)

dL=0.846+0.049V0

(4)

统计资料表明，行驶加速度随黄灯启亮瞬间车辆与停车线之间距离增大而减小[6]。因此仅选择黄灯启亮时不同速度到达的车辆至停车线距离最小的75组直行和28组左转末行车数据作为模型构建的数据。幂函数、S型函数和指数函数具有非负性不适用加速度为负值的情形。拟合结果如表3。

表3 行驶加速度-行驶速度模型拟合结果Table 3 Fitting results of running acceleration and running speed model

拟合结果表明：线性函数和对数函数可以较好地表征直行末行车和左转首停车行驶加速度与行驶速度之间的关系。拟合得到的模型与现有研究结果行驶加速度与行驶速度存在负相关关系相一致[6]。因此直行和左转行驶加速度-行驶速度模型可以分别表示为

aS=7.254-0.117V0

(5)

aL=3.187-0.932lnV0

(6)

第一类两难区经典GHM模型[7]：

(7)

式中：XS为黄灯启亮时车辆开始制动至完全停止的最小距离；XC为黄灯时间内车辆行驶的最大距离V0为黄灯启亮时刻瞬间速度；δ为制动感知反应时间；d为制动减速度；a为行驶减速度；τ为黄灯信号时长。

将公式(1)～式(6)分别代入式(7)，得到直行相位和左转专用相位第一类两难区模型：

(8)

(9)

3 黄灯信号时长优化

根据第一类两难区的定义：当XC小于XS时形成第一类两难区[8]。为明确限速值为60 km/h交叉口第一类两难区分布情况，以及两难区与黄灯信号时长和行驶速度之间的关系，利用MATLAB绘制XC-XS函数图像，如图2和图3。

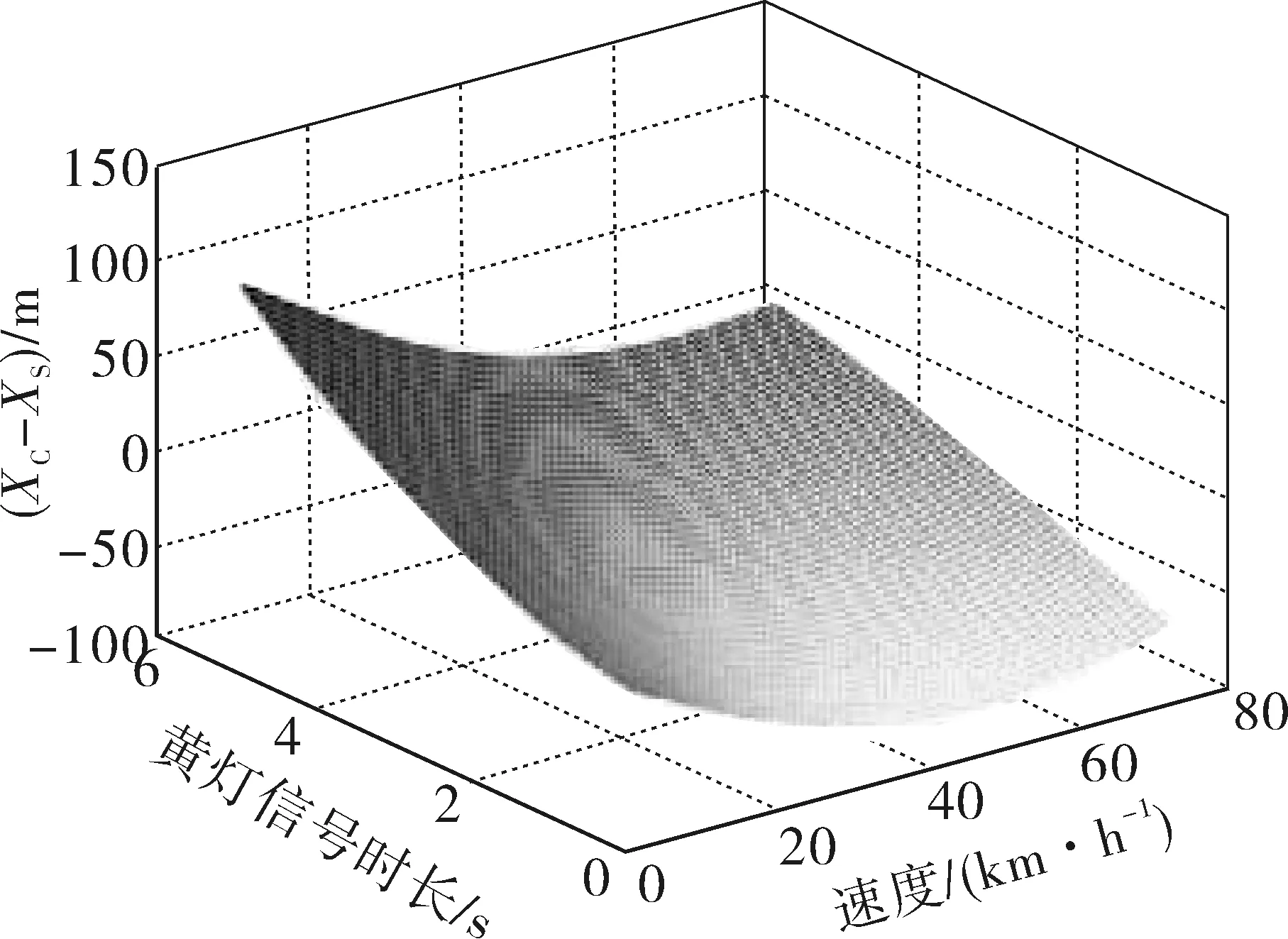
图2 直行相位第一类两难区分布Fig. 2 TypeⅠdilemma zone distribution of the straight phase

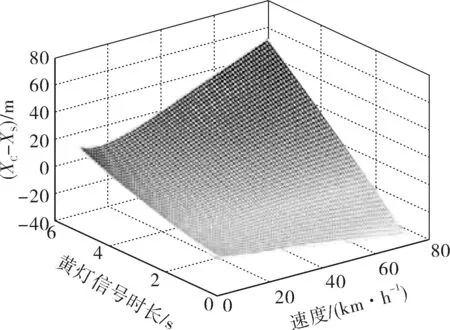
图3 左转专用相位第一类两难区分布Fig. 3 TypeⅠdilemma zone distribution of the exclusive left-turn phase

从图中可以看到，不论是直行相位还是左转专用相位第一类两难区的速度分布区间随着黄灯信号时长的增加而变小，这表明延长黄灯信号时长可以有效消除第一类两难区。当黄灯信号时长一定时，驾驶人陷入第一类两难区的风险随着速度的增加先增大后减小。当直行相位黄灯信号时长大于4.9 s时，可以完全消除第一类两难区；当左转专用相位黄灯时长大于3.4 s时，可以有效消除第一类两难区。

为进一步确定合理的黄灯信号时长，分别给出黄灯信号时长为3、4、5 s时的两难区边界曲线，如图4和图5。

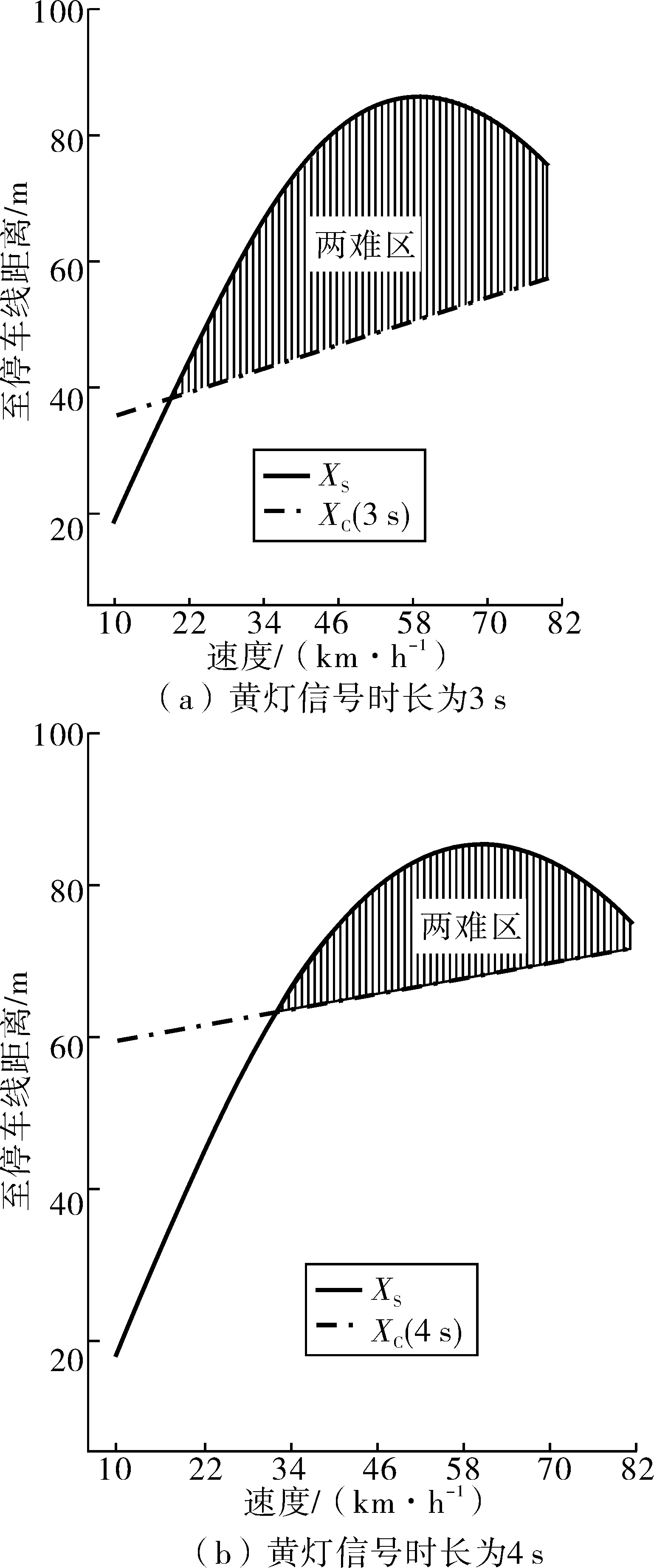
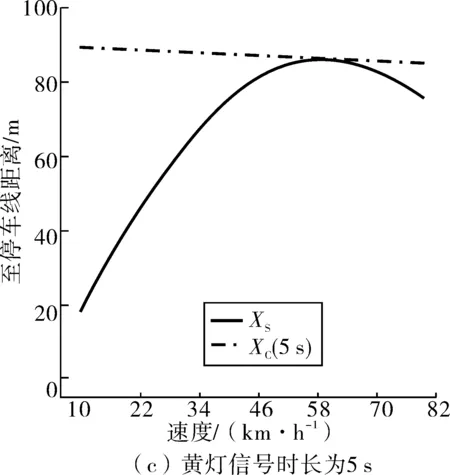
图4 不同黄灯信号时长下直行相位第一类两难区边界Fig. 4 TypeⅠdilemma zone boundary of the exclusive left-turn phase with different yellow signal duration

当黄灯信号时长为3 s时，位于直行车道上的驾驶人只有当驶入交叉口进口道速度小于19 km/h时，才能有效避免陷入第一类两难区。而对直行车行驶速度的统计分析发现，首停车15%位车速为20.54 km/h，末行车15%位车速为20.65 km/h，即若黄灯信号时长为3 s，则只有少于15%的驾驶人可以在不调整车辆行驶状态的条件下避免陷入第一类两难区。当黄灯信号时长为4 s时，位于直行车道上的驾驶人只有当驶入交叉口进口道速度小于32 km/h时，才能有效避免陷入第一类两难区。而对直行车行驶速度的统计分析发现，首停车50%位车速为30 km/h，末行车50%位车速为32.20 km/h，即若黄灯信号时长为4 s，则只有少于50%的驾驶人可以在不调整车辆行驶状态的条件下避免陷入第一类两难区。当黄灯信号时长为5 s时，可以完全保证驾驶人不陷入第一类两难区。故对限速值为60 km/h交叉口，直行相位黄灯信号时长宜设置为5 s。

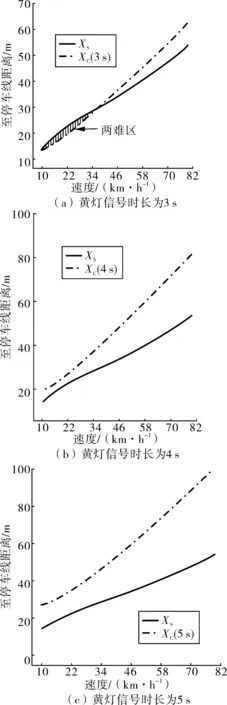
图5 不同黄灯信号时长下左转专用相位第一类两难区边界Fig. 5 TypeⅠdilemma zone boundary of the exclusive left-turn phase at different yellow signal duration

当黄灯信号时长为3 s时，位于左转车道上的驾驶人只有当驶入交叉口进口道速度大于38 km/h时，才能避免陷入第一类两难区中。对比左转车行驶速度的统计分析结果，首停车和末行车分别只有30.8%和29.7%行驶速度大于38 km/h，即若黄灯信号时长为3 s，则只有少于31%的驾驶人可以在不调整车辆行驶状态的条件下避免陷入第一类两难区。当黄灯信号时长为4 s时，位于左转车道上的驾驶人可以有效避免陷入第一类两难区中。当黄灯信号时长为5 s时，驾驶人也可以有效避免陷入第一类两难区的风险，但考虑到左转转用相位黄灯信号时长为4 s时已经可以保证驾驶人不陷入第一类两难区，继续延长黄灯信号时长可能增加驾驶人紧张和焦虑情绪，增大交叉口停车延误[9]，因此不建议将左转专用相位黄灯信号时长设置为5 s。故对于限速值为60 km/h交叉口，左转专用相位黄灯信号时长宜设置为4 s。

综上所述，在考虑第一类两难区的条件下，限速值为60 km/h信号交叉口直行相位黄灯信号时长优化取值为5 s，左转专用相位黄灯信号时长优化取值为4 s。

4 结 语

在采集实测数据的基础上，构建了直行相位和左转专用相位的第一类两难区模型。通过模型仿真表明：第一类两难区的速度分布区间随着黄灯信号时长的增加而变小，即延长黄灯信号时长可以有效消除第一类两难区；当黄灯信号时长一定时，驾驶人陷入第一类两难区的风险随着速度的增加先增大后减小。对于限速值为60 km/h的信号交叉口，黄灯信号时长设置为3 s时，驾驶人陷入第一类黄灯困境的风险较高，在直行相位黄灯信号时长为5 s和左转专用相位黄灯信号时长为4 s的情形下，可以有效避免驾驶人陷入第一类黄灯困境。

受数据采集的限制，笔者仅对限速值为60 km/h的信号交叉口黄灯时长优化问题进行研究，模型的实用性需要更多的实测数据进行验证，如针对限速值为50 km/h和70 km/h的交叉口开展实证研究。同时，信号灯倒计时、过街行人、交叉口的交通状态等因素都可能影响驾驶人的决策行为，从而导致车辆行驶参数发生变化，后续需要扩大样本，对相关因素进行深入研究，以完善模型参数。