基于巢式Logit模型的城际交通方式研究
江登英, 余 玲
(武汉理工大学 理学院, 湖北 武汉 430070)
0 引 言
随着经济和科技的迅速发展,目前,我国基本上形成了京津冀、长三角、珠三角以及海峡西岸、辽中南、武汉、江淮等城市群[1],城市群的轨道交通系统的发展将影响着我国城市发展的整体水平。因此,分析城际轨道交通方式划分,对城际轨道交通客流预测起到关键作用。
在现有研究中,国内外学者主要采用非集计方法对交通方式划分进行研究[2]。非集计模型是基于效用最大和随机效用原理,将出行者特性与交通方式特征进行结合,对交通方式划分有着十分广泛的应用。彭辉等[3]利用非集计Logit模型对城市群城际运输通道的旅客运输方式进行了研究;杨利强等[4]运用Mixed Logit模型主要研究了轨道交通出行旅客的时间价值;孙启鹏等[5]运用随机效用理论和非集计理论,基于Logit模型建立了基于动态广义费用的交通方式;陈喜春等[6]考虑了出行目的、旅客收入等多因素影响下铁路旅客出行时间价值的确定方法,建立了基于不同目、不同收入的效用函数;安文娟等[7]利用MD模型法对区域交通方式进行了研究;张宁等[8]运用多项Logit模型对居民出行方式选择行为进行建模;T.SATIENNAM等[9]利用BRT公交系统,对城市内汽车和摩托车进行评估,建立划分模型,对出行者选择进行分析。
笔者主要利用非集计理论与随机效用理论,从经济性、快速性、方便性、舒适性方面讨论了交通服务特性,建立效用函数,利用极大似然估计法对问卷调查数据进行处理并计算了效用函数参数;根据效用函数建立改进的巢式Logit模型,并用该模型对武汉至咸宁的城际交通方式进行研究。同时,将改进的巢式Logit模型与计算结果进行对比分析,从而深入探索改进模型的可行性与优越性。
1 城际旅客出行特征分析
城际轨道交通是城市群系统内新型的交通方式,其市场分担额不仅与轨道交通和其他交通方式的服务水平和技术经济特征有关,而且还受到城际旅客出行特征的影响。
城际旅客出行过程中,主要是从始发城市选择某种交通出行方式到达目的地城市,选择的交通方式有高速铁路、普通铁路、城际轨道、小汽车和城际客车等方式。旅客出行方式选择与城际交通方式服务属性、旅客自身经济水平和出行特征等因素有关,其中服务特性包括旅行的速度、票价、舒适性和便捷程度等;旅客自身经济特性主要体现在旅客收入情况和社会地位等,笔者主要考虑收入水平对出行选择的影响。随着科技发展,各交通运输方式性能越来越好,安全系数也越来越高,旅客在城际交通方式的选择上主要从经济性、快速性、便捷性、舒适性这4个方面进行考虑。
2 效用函数建立与模型分析
根据随机效用理论,旅客总是选择效用最大的方式出行。假设出行者n选择方案的集合为An,选择其中方案j的效用为Ujn,则该出行者从An中选择方案i的条件如式(1):
Uin>Ujn
(1)
式中:i≠j,j∈An。
根据效用最大化理论,出行者n选择交通方式i的概率Pin如式(2)。
Pin=Prob(Uin>Ujn)=Prob(Vin+εin>Vjn+εjn)
(2)

令Vin=θinXin;εin服从二重指数分布,则各概率项ε1n,ε2n, …,εjn的分布函数为F(ε1n,ε2n,L,εjn),概率密度函数为f(ε1n,ε2n,L,εjn)。这里假设f(εjn)服从二重指数分布,笔者采用Logit模型进行分析。
2.1 效用函数
效用值中固定项一般采用费用值表示,主要根据旅客经济属性、出行特征及出行方式特征综合衡量。参照研究中对效用函数因素的综合考虑,笔者主要从经济性、快速性、方便性、舒适性进行衡量。
2.1.1 经济性Ei
笔者主要考虑出行者所花的费用,其中高速铁路、普通铁路、城际轨道、城际客车的费用即为票价,小汽车的费用包含燃油费和过路费。
2.1.2 快速性Si
笔者主要考虑城际交通方式的在途时间,由于城际交通按时刻表出发且有专门的运输通道,不必考虑在途延误时间,可用运输过程中的时间与时间价值乘积来衡量快速性指标,如式(3):
Si=W(t)×(Li/Vi)
(3)
式中:W(t)为旅客出行时间价值;Li为选择第i种交通方式的出行距离;Vi为交通方式的运行速度。
2.1.3 便捷性Ci
便捷性主要考虑起止点城市及中途换乘城市的便捷程度,用费用Ci表示,如式(4)。
Ci=(ti1+ti2+ti3+Tig+Tih)W(t)
(4)
式中:ti1、ti2、ti3分别为第i种交通方式在起止点城市及换乘城市的换乘时间;Tig为第i种交通方式平均购票时间;Tih为第i种交通方式平均候车时间。
2.1.4 舒适性Gi
根据易富君等[10]的研究发现:旅客经过一定时间旅行后会产生生理和心理疲劳,消除疲劳感则需要时间来恢复。因此,舒适度可用疲劳恢复时间来衡量,如式(5):
(5)
式中:tmax为恢复疲劳所需最长时间;t为乘车时间;ai为无量纲参数;bi为单位旅行时间内的恢复时间强度系数,取值越大,表明恢复时间越长。根据实际情况,ai和bi的取值如表1。

表1 疲劳恢复时间参数Table 1 Time parameter of fatigue recovery
令tmax=15 h,并将相关参数代入式(5),可计算出疲劳恢复时间,并绘制疲劳恢复曲线,如图1。

图1 不同交通方式的疲劳恢复曲线Fig. 1 Fatigue recovery curve of different traffic modes
根据上述4项指标及效用函数中固定效用的线性函数关系,建立效用函数表达式Ui和固定效用函数表达式Vi分别为如式(6)、(7):
Ui=Vi+εi=θ1+θ2Ei+θ2Si+θ4Ci+θ5Gi+εi
(6)
Vi=θ1+θ2Ei+θ2Si+θ4Ci+θ5Gi
(7)
式中:εi为选择第i种交通方式的随机变量;θ1~θ5分别为效用函数固定项系数。
2.2 时间价值
旅客时间价值客观上反映了旅客在旅行过程中所耗费的时间成本,涵盖许多对旅客起决策作用的因素,成为影响旅客决策关键性指标。笔者根据问卷调查,采用工资法计算时间价值,如式(8):
ti=Ii/dp
(8)
式中:Ii为旅客的月收入;d为工作天数;p为每天工作时间。
3 改进巢式Logit模型
利用非集计理论,对城际交通方式划分进行研究。常用的非集计模型是Logit模型,包括多项Logit模型、巢式Logit模型等。由于多项Logit模型(MNL模型)有自身的假设条件,各选择枝之间必须相互独立,而城际交通系统中小汽车和城际客车之间、普通铁路和高速铁路之间存在较大相关性,因此不能直接利用MNL模型进行求解。为避免MNL模型的IIA特性并弥补模型的不足,对MNL模型进行改进,将具有相关性的交通方式置于同一巢内,相互独立的则置于不同巢中,各巢之间相互独立。这里主要利用巢式Logit模型[11]对城市群城际交通方式进行划分。层次划分正确性主要是通过指标IV(包容值)[12]的参数值大小来确定,IV参数值应该处于0和1之间,否则表明层次划分不合理,构建的分层树状结构如图2。

图2 城际不同交通方式树状结构Fig. 2 Tree structure of different intercity traffic modes
根据巢式Logit模型结构图,利用条件概率计算各选择枝的分担率。
3.1 改进巢式Logit模型
笔者选择巢式Logit模型对城际各运输方式的客运分担率进行确定,为消除指数级增长而导致结果差异扩大,故采用改进巢式Logit模型。
假设在虚拟选择枝A下,选择交通方式i的概率为P(i|A),其中第i种交通方式的固定效用为Vi。当i=1、2、3时,则有式(9):
(9)

对于虚拟选择枝B,同样可求出各选择枝的概率。当i=4、5时,则有式(10):
(10)


(11)

(12)
式中:i=1、2、3;j=4、5;a、b、μ分别为参数。
3.2 模型参数求解
对于效用函数的参数,笔者采用极大似然估计法进行求解。若出行者n的固定效用Vin=θinXin,则有θin=(θ1in,θ2in,θ3in,θ4in,θ5in),Xin=(1,Ein,Sin,Cin,Gin)T,θin为参数向量。令样本数目为N,则定义:
则似然函数L*有式(13):
i∈An)
(13)
对式(13)两边取对数,结合Pin求对数似然函数如式(14):
(14)
式中:J=A、B。
若出行者选择虚拟选择枝A下交通方式,当i=1、2、3时,则有式(15):
(15)
若出行者选择虚拟选择枝B下交通方式,当i=4、5时,则有式(16):
(16)

4 实证分析
笔者以武汉城市群中武汉至咸宁的城际旅客为例,对城际各交通客运方式划分模型的可行性和有效性进行研究。
结合武汉至咸宁城际运输系统实际情况,主要考虑高速铁路、普通铁路、城际轨道、小汽车、城际客车等客运分担率。首先通过问卷调查,分别利用改进巢式Logit模型和巢式Logit模型确定不同收入出行者对各因素的权重,计算出两种模型对应的效用值;然后根据改进巢式Logit模型和巢式Logit模型不同效用值计算对应的分担率;最后将两种模型计算的分担率与实际分担率进行对比,通过分析来指导以后武汉城际交通方式的管理和划分。
4.1 效用函数值计算
笔者结合调查,确定不同交通方式对应的各影响因素,根据极大似然估计法分别计算改进巢式Logit模型和巢式Logit模型的固定效用函数系数,并根据相关数据进一步计算相应效用值。
4.1.1 效用函数影响因素
问卷调查中,笔者将旅客的月收入分为4类:3 500元以下、3 500~5 000元、5 000~8 000元、8 000元以上。2016年—2017年期间,在不同季节的不同时间段,同时对不同交通方式出行者共进行了100次问卷调查,从调查结果中选取8 000个有效调查结果,统计收入等级、乘车方式、买票时间、票价、车内时间、候车时间及换乘费用,并将相关数据代入式(3)~(5),计算出对应的经济性、快速性、便捷性、舒适性指标。
由于不同收入旅客的时间价值不同,经济性用票价表示,快速性用在途时间表示,便捷性用换乘时间、平均购票时间和平均候车时间表示,舒适性用疲劳恢复时间表示,则不同交通方式中各影响因素对应数据如表2。
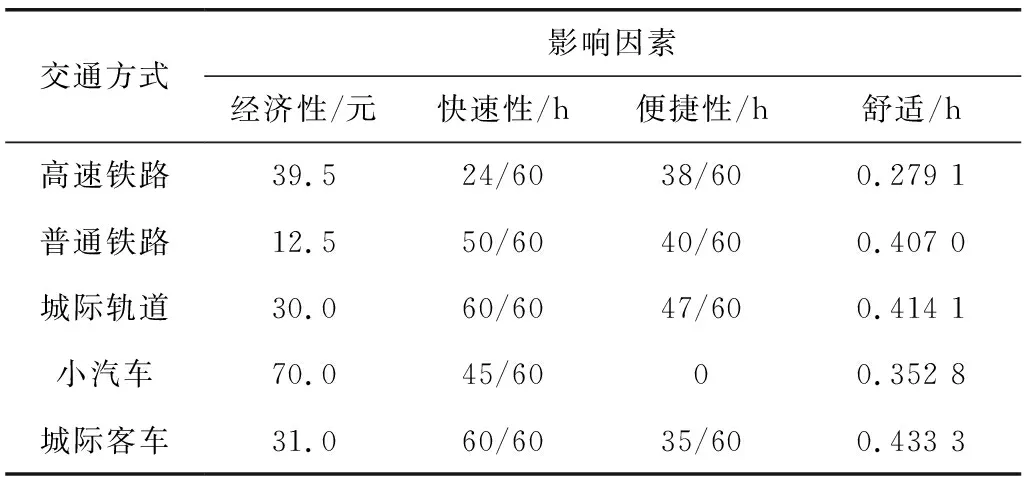
表2 不同交通方式各影响因素Table 2 Impact factor of different traffic modes
假设每天工作时间为8 h,每月工作22 d,将月收入小于3 500元的人群记为3 500,大于8 000元的记为8 000,其他取两者的算数平均值,将相关时间和收入代入式(8),计算出对应时间价值如表3。

表3 不同收入旅客的时间价值Table 3 Time value of travelers with different income
4.1.2 权重系数
对固定效用的系数,笔者结合调查结果及表2相关数据,根据式(13)~(16),运用极大似然估计法对改进巢式Logit模型的固定效用函数系数进行计算,得到相应权重系数如表4;运用极大似然估计法根据调查结果和表2相关数据,令a=b=1,计算巢式Logit模型固定效用函数的系数,得到相应权重系数如表5。

表4 改进模型的固定效用权重系数Table 4 Fixed utility weight coefficient of the improved model

表5 巢式Logit模型的固定效用权重系数Table 5 Fixed utility weight coefficient of nested Logit model
4.1.3 固定效用值
根据表2~4相关数据及式(7),计算改进巢式Logit模型中不同收入等级的出行者在选择不同交通方式出行时对应的费用值(即效用的相反数),得到费用值如表6;根据表2、3、5的相关数据及巢式Logit模型,在模型计算中令a=0.038,b=0.036,μ=0.05,得到相关费用值如表7。

表6 改进模型的相关费用值Table 6 Cost value of the improved model

表7 巢式Logit模型相关的费用值Table 7 Cost value of nested Logit model
4.2 分担率计算
将表6中固定效用值代入改进巢式Logit模型中,结合式(9)~(11),分别计算不同收入者的各交通方式分担率,如表8;结合表7中固定效用值和巢式Logit模型的规则,计算对应的分担率,如表9。
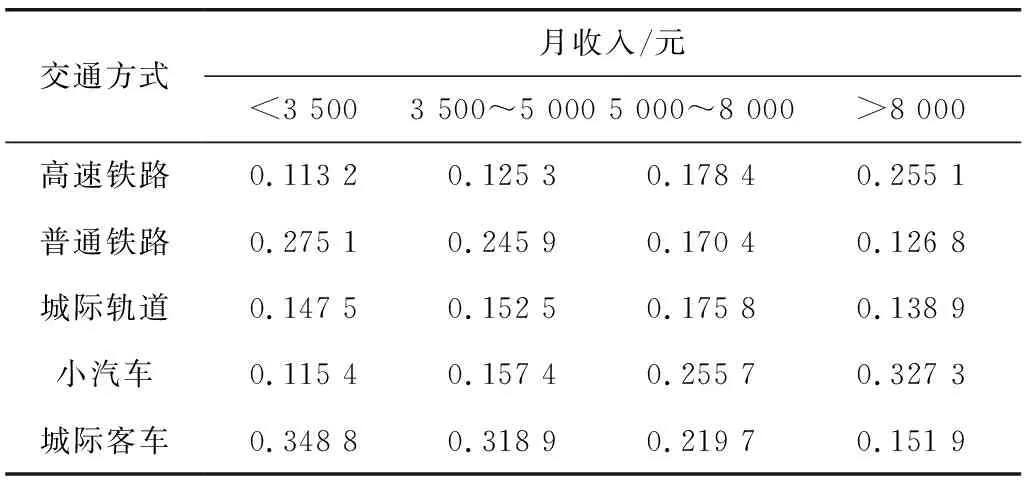
表8 改进模型的相应的分担率Table 8 Corresponding share rates of the improved model

表9 巢式Logit模型相应的分担率Table 9 Corresponding share rates of nested Logit model
为分析各交通方式总体分担率的情况,笔者根据对应模型计算各交通方式的分担率,再将2016年—2017年期间武汉至咸宁的实际客流量与两种模型预测结果进行对比分析,如表10。

表10 分担率对比分析Table 10 Comparative analysis of the share rates %
通过对比分析发现:两种模型计算结果与实际调查结果基本保持一致,原模型(巢式Logit模型)在部分交通方式上虽比改进模型(改进巢式Logit模型)更加接近实际统计结果;但由于改进模型在利用极大似然估计法确定固定效用函数系数时,根据对城市群的城际交通方式进行层次划分特点,各选择枝采用改进的概率计算方法,从而确定模型相关权重系数;此外,在计算模型效用值时,充分考虑模型整体性及不同交通方式之间的关联性,用相对效用代替绝对效用,避免了普通铁路和城际轨道陷入局部孤立的变化中。比较发现:目前普通铁路、城际轨道和城际客车在人们出行中占重要地位;未来城际轨道、小汽车及高速铁路分担率将会增大;普通铁路和城际客车分担率将会减小,这与目前武汉城际交通方式发展趋势一致,对未来武汉和其他城市群的城际交通建设和规划有着重要参考价值和指导作用。
5 结 语
笔者根据非集计理论建立改进的巢式Logit模型,用相对效用来代替绝对效用,从而对巢式Logit模型进行改进。将城际出行者特征与交通方式特征结合,从经济性、快速性、便捷性、舒适性这4个方面建立效用函数。用改进巢式Logit模型和巢式Logit模型预测武汉至咸宁各交通方式的分担率,并与实际客流量进行对比,验证了改进巢式Logit模型用于城际各交通方式划分及预测的可行性和优越性,这对未来武汉城市群及其他省市城际交通合理规划起着重要作用。
在后期研究中,根据研究结果,笔者将进一步研究城际各交通方式在不同时期客流量预测的相关问题,对相应交通工具分配方案进行优化,从而达到节约能源、降低费用和碳排放量的目的。

