An Optimal Charging/Discharging Strategy for Smart Electrical Car Parks

(School of Electrical and Data Engineering, University of Technology Sydney, Ultimo, NSW, Australia)

Abstract: This paper presents a smart electrical car park model where the power flows among electrical vehicles(EVs) as well as between EVs and the main grid. Based on this model, an optimal charging/discharging scheme is proposed. The fluctuation of hourly electricity rates is considered in this strategy to select a proper charging/discharging rate for each EV with less expenditure during each charging period. The proposed smart electrical car park is able to buy or sell electricity in the form of active and/or reactive power, i.e. kWh and/or kVARh, from or to the main grid to improve the power quality. According to the current state of charge of the EV’s battery bank, customers and the grid demands,a control center makes the decisions and sends the instructions of specific charging/discharging mode to each charging station. The performance of the proposed charging/discharging algorithm is simulated in Matlab. A comparison between the proposed and the unregulated charging/discharging strategies has been implemented. The results demonstrate that the proposed scheme can achieve better economic profits for EV customers and increase the commercial benefits for the car park owner.

Keywords: Smart car park, charging/discharging method, V2G.

1 Introduction

Due to the fast depletion of fossil fuels and large quantities of greenhouse gas emissions, efficient and clean electric vehicles(EVs) have drawn great attention recently[1-2]. No doubt, they will be widely used in the near future. Furthermore, the battery banks of EVs consume huge amounts of electricity from the power grid. New vehicle-to-grid(V2G) and vehicle-to-vehicle(V2V) technologies are being developed to store the energy in these rechargeable batteries[3-4]. This helps balancing of the power grid between the demand and supply, and delivering the energy among EVs[5-7].

Compared with EVs used in public transportation,personal EVs are much larger in number, but are employed for only around 4% of the day for transport[8].Since they are parked for about 96% of the time, it would be a good idea to develop their energy storage capability to provide secondary service in the electricity market[9-12]. A smart electrical car park, with a large number of parked EVs, can be regarded as a large capacity energy storage unit. Taking advantage of the new V2G technology and appropriate economic strategy,this car park is able to yield profits by providing effective services to the EV customers and the electricity supplier[13-16]. Inspired by this issue, we propose an approach of a smart electrical car park to enable the personal EVs to participate in the energy market.

In recent electric vehicles literature, considering the EV batteries as controllable parts in the power system,numerous papers pay attention to optimizing EVs charging and discharging modes to participate in ancillary services in the smart grid[17]. Some works have been studied to minimize the expense for EVs’ owner or reduce the total cost of the aggregator separately. The work of [7,18] and [19] indicate that the proposed charging strategies using the real realistic analysis of EVs driving profiles can cut down the charging cost for EV owners. In [1], Nguyen et al. proposed a smart charging and discharging method for multiple plug-in hybrid electric vehicles(PHEVs) in a building car park to optimize the energy consumption for this building. An energy cost-sharing model and a distributed algorithm were presented to minimize the peak load and the total energy cost at the same time.

With bidirectional chargers, the EV batteries can exchange the active power with the utility grid in G2V and V2G operations. The EV batteries can also meet the reactive power command from the grid, which is known as vehicle-for-grid (V4G). In this operation mode, EV batteries function as static var compensators, capacitor banks, etc. In this paper, the proposed car park system also benefits from supplying the reactive power to the grid with the agreed annual rate.

In general, novelties of this paper can be summarized as follows:

(1) Taking the real hourly electricity rate and EVs batteries constraints into consideration, the proposed smart car park system can minimize the expenditure for EV owners and reduce the cost for the car park operators at the same time.

(2) The proposed control method enables the EVs to be plugged in the grid during the off-peak hours.Meanwhile, the EVs discharge the power to the grid during the peak hours to balance the loads. The model with the optimal charging scheme is simulated in Matlab with an optimization problem solver named Cplex.

(3) Apart from G2V and V2G operations, the new V4G operation achieves the bidirectional reactive power flow between the grid and the smart car park system. An extra economic benefit can be obtained for the system operator.

The rest of this paper is organized as follows.Section 2 sketches the smart electrical car park model.An optimal charging strategy is proposed in Section 3,which calculates the charging rates of EVs during one-time slot economically and reasonably. Section 4 investigates the possible parking hours and charging demands of EVs. Section 5 presents and discusses the simulation results pertaining to the costs of EVs customers and the benefits of car park owners with the proposed optimal charging/discharging method. Finally,conclusions are drawn in Section 6.

2 System modelling

In this section, a smart electrical car park model is introduced. As shown in Fig.1, this smart electrical car park system is composed of numerous smart charging stations, a center controller and energy storage devices.The smart charging stations have touch screen panels to interface with the customers, which enables the customers to type their demands and special needs.These touch panels are connected with a control center via either cable or Wi-Fi[13]. The central controller collects the basic information from the main grid and EVs. The EVs’ information includes battery capacity characteristics (i.e., rated capacity, available capacity,voltages, expected charging and discharging currents),the initial state of charge(SOC), the final SOC, the parking time(arrival and departure time), etc. The charging rates of EVs obtained from the charging scheme are sent to the chargers by the controller every time slot. With the G2V and V2G technologies, EV batteries can exchange the active power with the main grid. However, the active power commands from the EV batteries and the utility grid might be different sometimes. Therefore, energy storage devices, such as super-capacitor banks, are used to compensate the power difference between the grid and the EV batteries within its capacity. It is of great assistance to keep the balance of the active power for the grid[20].

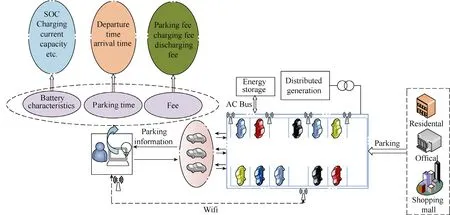
Fig.1 Framework of the smart car park system

Apart from delivering the active power, this car park can supply the reactive power to support the grid in the V4G operation. During this operation, EV batteries function as static var compensators. It is important to note that the EV batteries lifetime cannot be reduced during the reactive power operation[21]. Other components,such as the dc-link capacitors might be affected due to the increasing charging-discharging cycles.

This kind of smart electrical car parks can be located in office, shopping mall, and residential community in the future. According to the charging time in the report[22], 30 minutes is the minimum charging period for EVs parking in office, home, public or commercial parking lots. Therefore, in our paper, the time slot (Δt) is set as 30 minutes. Note that the time slot can be adjusted according to different requirements from different types of smart car parks.

Based on the designed time slot, the working time of smart electrical car parks is divided into several control periods. A single decimal number between 0 and 24 is used to represent the time. For example, if the car park opens from 7 A.M. to 9 P.M., it is divided into 28 time blocks (N=28) with each time block equal to 30 minutes. For easy reference, all the major notations are listed in Table 1.

Table 1 Major notations

2.1 Range of charging/discharging powers

In order to avoid overcharging or over-discharging of EV batteries, the charging power constraint for each EV should be considered before participating in the G2V and V2G process. Since the charging rate varies depending on the types and conditions of EV batteries,EVs are divided into several categories according to the initial SOC, the final SOC, the charging type and the parking time. The information can be set by the customers through the touchscreen panels.

A parameter L is introduced to represent the charging type, defined as

Some of EVs only park for a short time, thus, the priority objective is to meet the demand of customers rather than to charge more economically. In order to solve this problem, the maximum idle parking time for mth EV tm,p,maxis employed, which is calculated as

where tm,pis the parking time, Em,needthe needed charging/discharging energy, and pm,maxthe maximum charging/discharging power, for mth EV. If the maximum idle parking time tm,p,maxis less than one-time slot Δt, the charging or discharging rate is set to the maximum value.

Finally, according to the above analysis, the charging power range of EVs is summarized in Table 2.

2.2 Electricity price

The hourly electricity price is a function of the time,which can be denoted as f(t). Specifically, the hourly electricity prices in NSW, Australia during one month(January 1 ～ 31, 2015) were obtained from Australian Energy Market Operator(AEMO)[23], which is responsible for the National Electricity Market of south-eastern Australia. Average hourly electricity prices over a month, used for simulation during the car park opening hours from 7 A.M. to 10 P.M., are presented in Fig.2. It is used to calculate the electricity fee for the EVs drivers and the car park owner.

The car park owner purchases the electricity from the grid at a wholesale rate, as well as selling it to the grid[5]. Meanwhile, the EV customers buy or sell it at a general price as individuals. Therefore, four pricecoefficients (δ1, δ2, δ3and δ4), are introduced to describe the prices for EV customers and car park owners buying and selling electricity, respectively.

The prices of EV customers and car park owners charging and discharging electricity can be formulated as

Table 2 Range of charging/discharging power

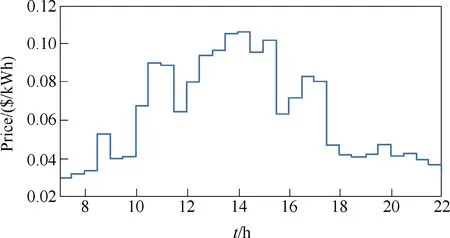
Fig.2 Average hourly prices of electricity in NSW

where k=1 means EV customers charge the electricity from the grid, then δ1is equal to 1, as the EVs act as individual customers; K = 2 means EV customers discharge the electricity to the grid; K = 3 or 4 means the car park charges electricity or discharges energy,respectively. Normally, δ3is less than or equal to δ1since the car park buys electricity at a wholesale price.δ2is less than or equal to δ4because the car park has the ability to sell a large amount of electricity to the grid according to its demands, while an EV customer just sells quite little electricity to the car park as an individual at random periods of time.

2.3 Grid demand

Another benefit for this smart electrical car park is that it provides the stored energy to the grid during peak hours and behaves as a load during off-peak hours.

Fig.3 exemplifies the relationship between the total electricity demand and the average regional reference price during one day, which is also obtained from AEMO[23]. It can be observed that the electricity price is high when the demand is increasing, and vice versa.Therefore, it can be assumed that the electricity demand of the main grid is proportional to the electricity price generally. This means that if EVs discharge the energy to the main grid during periods of high loading (e.g.,8～24h), it can relieve the pressure on the grid. On the other hand, more EVs can be connected to the grid to be charged during off-peak hours (e.g., 0～8h).

2.4 Profits of smart electrical car parks

The profit of a smart electrical car park is composed of two parts, as depicted in Fig.4. One is the electricity price gap by exchanging the active power between the EVs and the grid. Another is the income by working as a static var compensator to provide the reactive power.The profit of exchanging the active power can be divided into two subparts: the charging profit and the discharging profit.

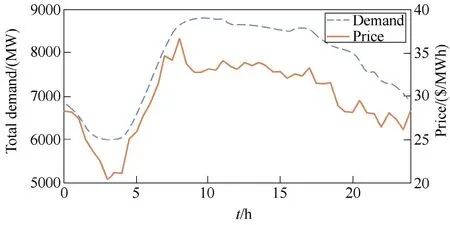
Fig.3 Electricity demand and average electricity price

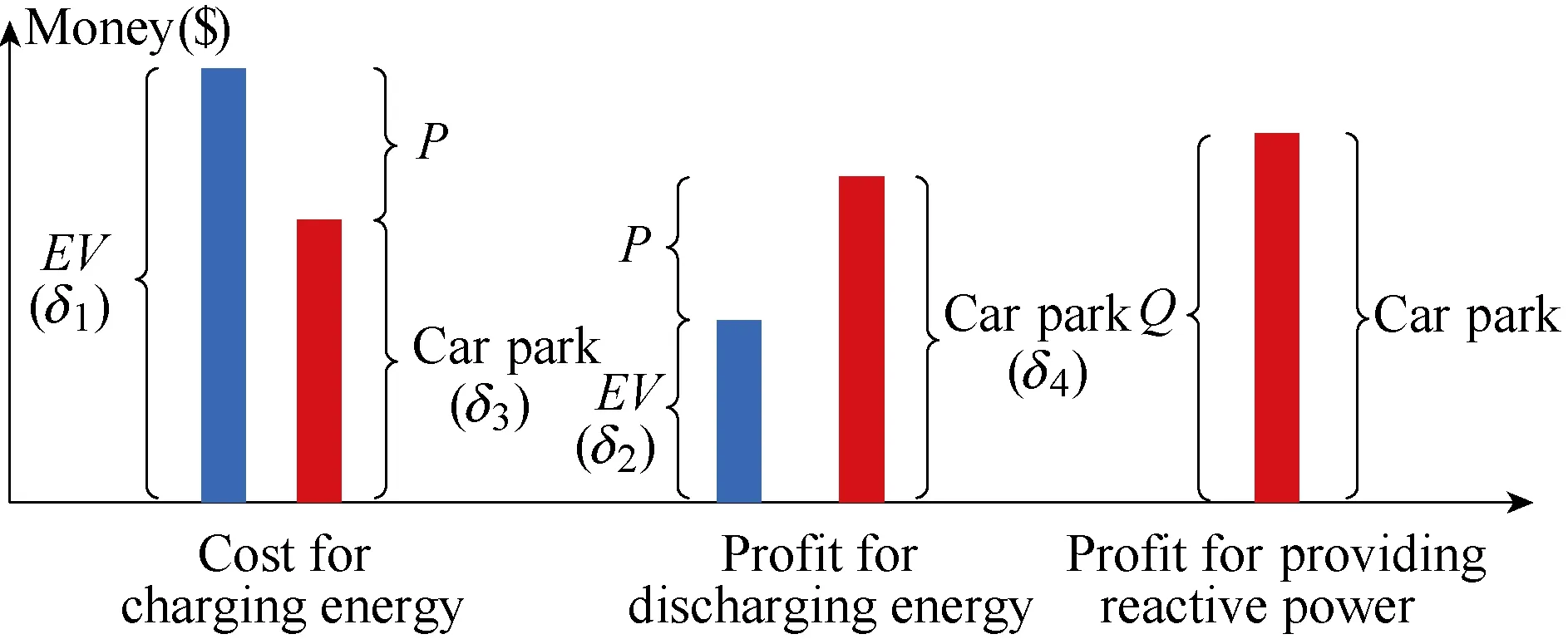
Fig.4 Main profits of smart electrical car parks

The profit of providing the active power to the grid can be calculated as

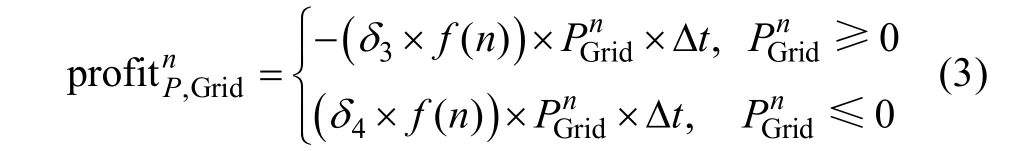
Due to the energy storage devices, the active power provided by the grid during nth time slot can be calculated as

Then, taking (2)～(4) into consideration, the total profit for the car park selling or buying the active power among the grid and EVs can be calculated as where M is the total number of EVs parking during an nth time slot, N the total number of periods during

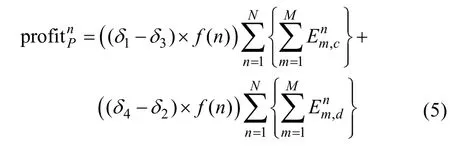
the opening time for the car park,andthe charging or discharging energy for mth EV during nth time slot, respectively. Then, this profit is the sum of the charging and discharging income from the grid and EV owners.

The second profit of providing the active power to the grid is shown as

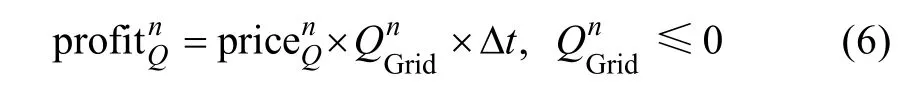
Then according to (5) and (6), the overall profit for the car park during nth time slot can be calculated as:

3 Proposed charging/discharging scheme

3.1 Objective function

In this section, an optimal charging scheme is proposed to solve the problem.

In this model, the electricity price, charging time and desired SOC are all taken into consideration to allow EVs to participate in the V2G/G2V system. Note that the reactive power reference is set to be zero to operate at the unity power factor normally. In this operation, no reactive power profit is made. When the main grid hungers for the reactive power, the car park provides the reactive power to the grid as requested or at the maximum supply value. It can clearly be seen that the reactive power profit is always larger than or equal to zero for the car park. Therefore, the reactive power can be regarded as a constant factor in the charging/discharging scheme. Then, according to (7), the objective function J at any time slot n can be described as

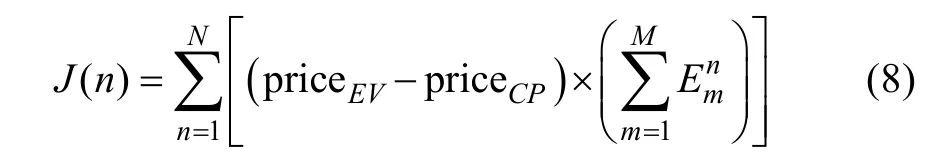
where priceEVand priceCPare the electricity prices for EV customers and the car park owner, respectively.Based on (2), they can be calculated as:

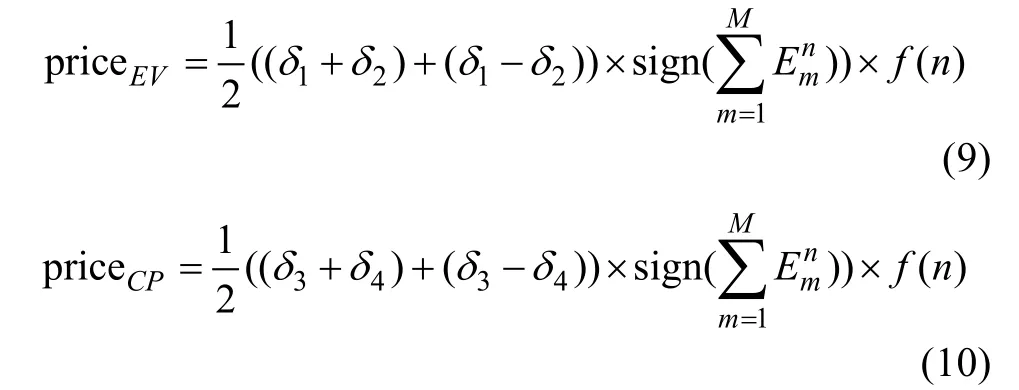
Substituting (9) and (10) into (8) yields (11)

We assume that the electricity price for purchasing and selling are the same in the simulation (i.e., δ1= δ2.and δ3= δ4). Under this operation, the profit for the EV driver is at a most conservative state. With increasing of the electricity price gap between the charging and discharging, the benefits for EV drivers and the car park will increase. Then, the objective function J can be rewritten as

3.2 System constraints

The following constraints are defined for the proposed algorithm.

Constraint (13) ensures that the charging rate calculated by the optimal charging scheme will remain within the range of the charging power. Constraints(14)～(16) assign the charging energy during each time slot and show the current energy stored in batteries. In this way, EVs can be charged or discharged to the anticipated value. Constraint (17) is proposed to avoid overcharge or over-discharge. In order to extend the battery lifetime, the range of SOCs is set as a default range between 20% and 90% by the car park if car owners do not set it[23], as shown in constraint (18).However, if the final SOC is set out of the range by customers, the EVs should be charged or discharged to the desired values. For example, if an EV customer set the final SOC as 100%, the range of this EV’s SOC will be updated between 20% and 100%. Constraints (19) ～(20) show that the storage device is designed to compensate the active power difference between the EVs and grid demands within its maximum capacity.

3.3 Algorithm

The mathematics model is set up in Matlab by using Yalmip Wiki and the optimization problem is solved by the solver-IBM ILOG Cplex Optimizer 12.6.1.

At the beginning of one day, the central controller updates the system information, such as the amount of the energy stored in energy devices. Then, at the beginning of a time slot Δt, the central controller performs the following actions, as presented in Fig.5.

4 Parking hours and charging demands of EVs

4.1 Distribution of EVs’ parking time

Fig.5 Flow chart of the algorithm

In order to develop an accurate car park system model, the probability density function of EVs parking information is required. An office-type car park, located in the underground level of Building 10 at the University of Technology Sydney(UTS), is investigated. Its opening hour is from 7 A.M. to 10 P.M. from Monday to Friday with 150 parking positions. The survey on this UTS car park during a normal working week indicates the parking time of vehicles, as depicted in Fig.6, which is a normally distributed random variable with μ=8.299h and σ=1.814h. The distribution function for parking hours is given by

As shown in Fig.6, most of the vehicles will park more than 3 hours. Their parking duration times are enough to enable EVs to participate in secondary service in the electricity market.

Similarly, arrival and departure times follow normal distributions as well, as depicted in Figs.7 and 8,respectively. Table 3 lists the distribution parameters of them.

Fig.6 Distribution of parking duration time

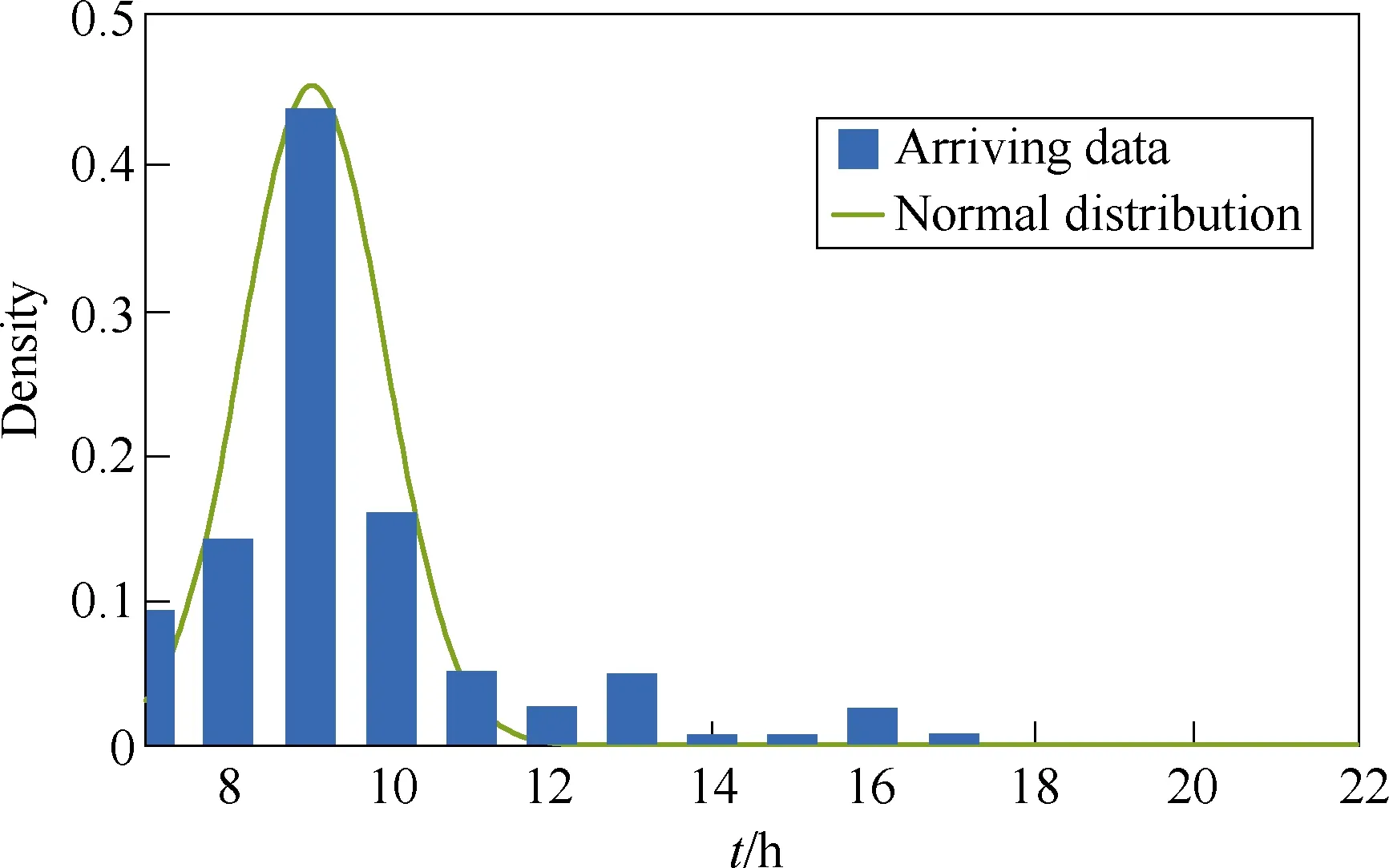
Fig.7 Distribution of arriving time

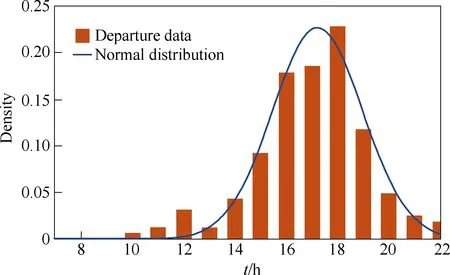
Fig.8 Distribution of departure time

Table 3 Distribution parameters of arriving and departure times

Although these cars are traditional vehicles, it is reasonable to assume that the behaviours for divers would change little in the future. Therefore, the information from the survey can be utilized as the EV parking information.

4.2 Simulation settings

All EV customers are assumed to have set their demands via the touch screen panels after parking, such as SOCm,fin, L, tm,p, pm,c,max, pm,d,max. According to the behavior of drivers[1], Table 4 tabulates the range of initial SOCs, the range of final SOCs and the range of capacity of EVs. Meanwhile, four electricity price coefficients (δ1, δ2, δ3and δ4) are set as well.

5 Results and discussions

In this section, the simulations are performed by the proposed charging algorithm and the results running in the car park with sizes of M = {100, 200, 300, 400, 500}are presented, respectively.

Table 4 Simulation settings

Fig.9 compares the curve of desired SOCs and final SOCs. It can be seen that all of the EVs are charged to the desired SOCs prior to their departure times.

Three EVs (EV 17, EV 53 and EV 84) are chosen randomly to observe their SOCs and the variation of their SOCs along with the fluctuation of hourly electricity prices, as shown in Fig.10. EV 53, which comes to the car park at 1:30 P.M. and leaves at 2:30 P.M., can only be discharged. It is parked for only 1 hour which includes only two time slots. During these two time slots,the curve of its SOC shows that it is discharged at a larger rate during the second time slot, which has a higher price for the selling electricity than the first one.

Similarly, EV 84, which can only be charged,comes in at 2:30 P.M. and leaves at 4:30 P.M. During the parking periods, it is charged quickly from 3:30 P.M to its departure time, because the electricity price is much lower during this period. The EV 17, with the charging type L set to zero, is set to be charged and discharged several times during the parking period and leaves at the desired SOC value. It is also set to be charged during low-price periods and be discharged during high-price periods.

An unregulated charging/discharging scheme is used to compare with the proposed method. With this method, EVs will be charged/discharged with an average power rate during the parking hours. The power rate is calculated by using the expected charging/discharging energy divided by the parking time. It can be seen from Figs.11 and 12 that the costs for EVs customers and the car park owner with the charging scheme are much lower than the ones with the traditional scheme,respectively. Specifically, the costs for customers can be reduced by 47% on average, compared with the unregulated charging method.

Fig.9 Curve of final SOCs and desired SOCs

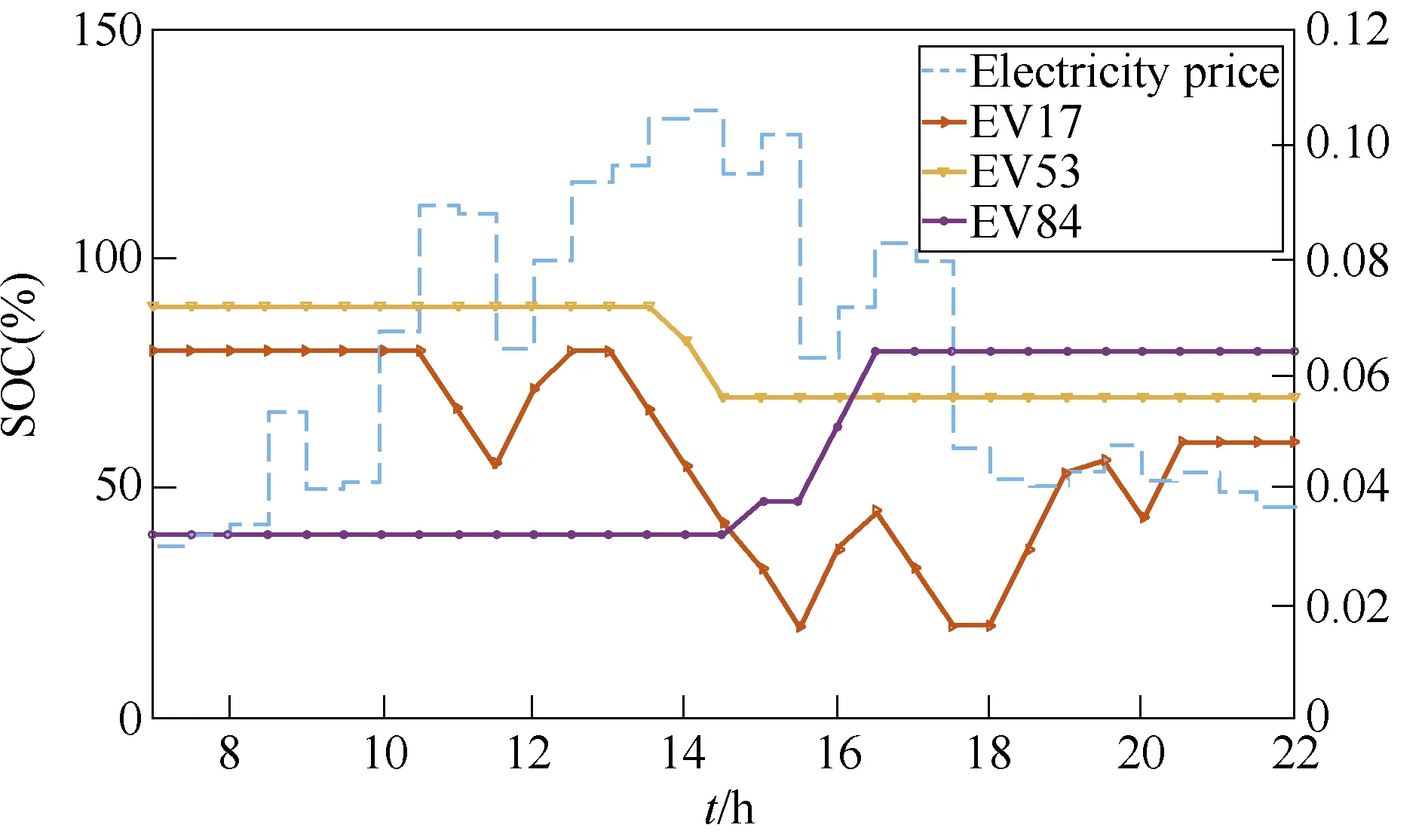
Fig.10 Three EVs’ SOCs and hourly prices

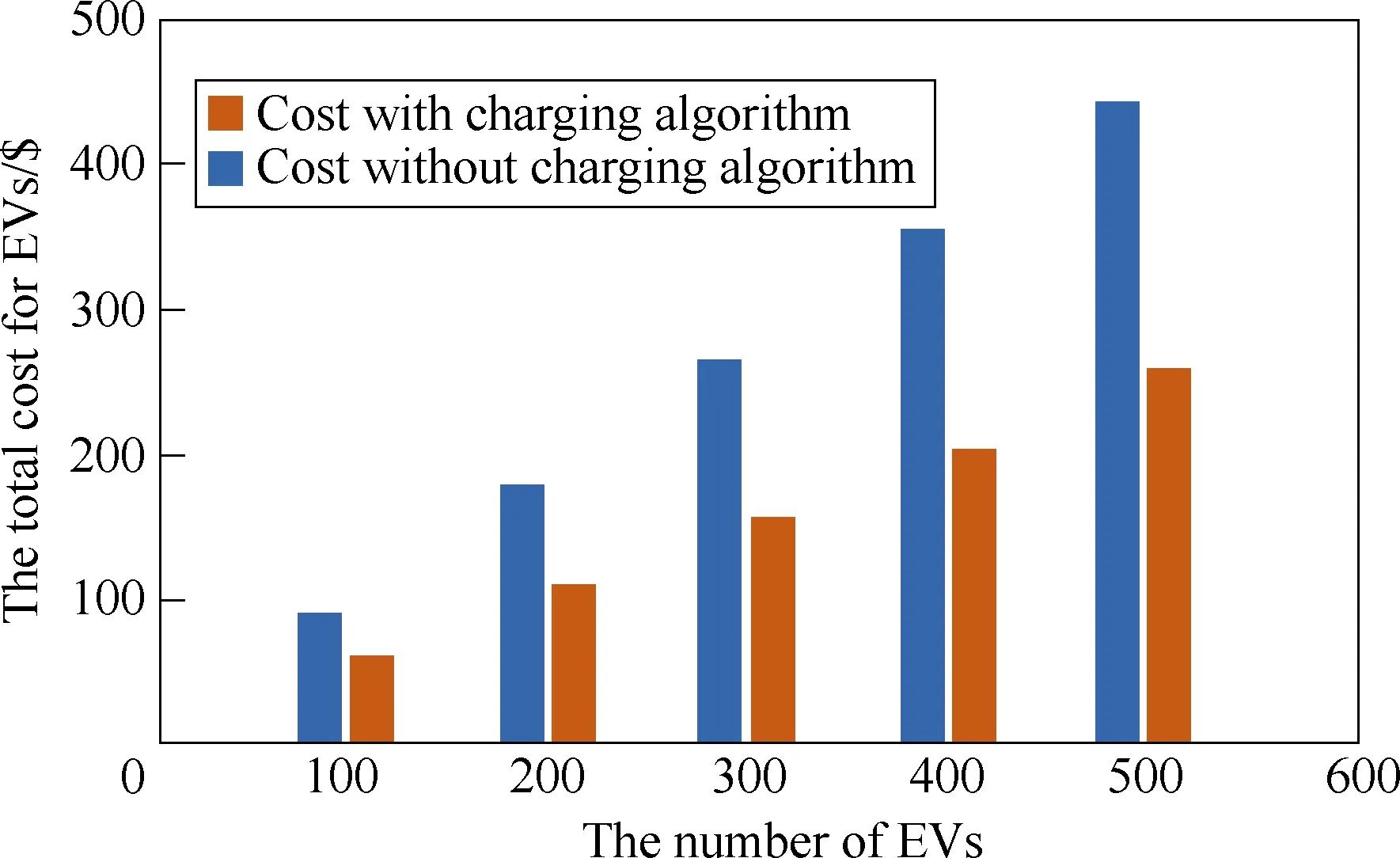
Fig.11 Total costs for EVs

Fig.12 Total costs for car park

Fig.12 shows that the cost of the car park with the optimal scheme are negative, which means that the car park does not have to pay money to the power grid even when charging energy from it.

In Fig.13, the profits for the car park using the proposed charging method are around 3 times of that obtained by unregulated charging with different car park sizes M.

6 Conclusion

This paper presents a smart electrical car park model involving the V2G and G2V technology, which enables the bidirectional power flow. In order to calculate the optimal charging powers, the real hourly electricity price is collected and analysed. An optimal charging scheme has been proposed. It aims at making profits for the car park owner and minimizing the cost for EV customers. The simulation is performed in Matlab with the real-world parking information collected from an underground car park at UTS.Compared with the results of the conventional charging algorithm, the simulation results show that the benefit of the car park owner can be increased by approximately 300%. Also, the related costs for EV customers is reduced by 47% on average. At the same time, the SOCs of EVs at their departure times can reach the expected values set by customers. Furthermore, this system provides the solution that is very close to optimal, which can be of great benefits to customers, car park owners and the main grid simultaneously.

Fig.13 Profits of car park