开发教学资源,构建高效课堂
江苏泰州市康和实验小学(225300) 朱月萍
苏教版小学数学教材从2013年开始,启用了新的版本,通过前十多年的教学实践,教师对于“用教材教”的理念已有深刻的认识,深深认识到教材是我们进行教学活动的一个重要资源。在平时教学中我们既要基于教材,同时又要对教材进行科学的二次开发,这样才能使我们的教学适应学生的学习需求,从而有效促进学生的发展。本文就教材中的例题、活动问题等素材,谈谈如何对教材实施有效的二次开发,构建高效课堂。
一、调整例题难度,贴近学生实际
教材是教材编写组统一开发的文本资料,虽经过专家、一线教师反复研究,但学生的学习基础存在地域、认知等差异,对此,教材根本无法兼顾不同学生的需求。作为一线教师的我们,应针对学生的差异性,对例题进行一系列的调整,使例题教学更加贴近学生的实际。
【案例1】苏教版教材小学数学第十册第三单元例9。
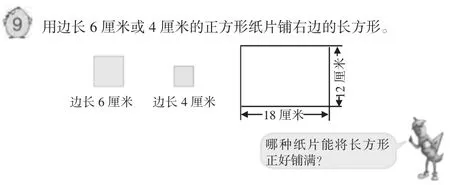
原题分析:本例题的设计意图有如下5个方面。(1)让学生用边长6厘米或者4厘米的正方形纸片铺长18厘米、宽12厘米的长方形。在学生活动、交流后得出边长6厘米的纸片可以铺满长方形,而边长4厘米的纸片却不行。同时呈现这两种正方形铺长方形的示意图。(2)引导学生观察上述示意图,具体分析长方形长和宽与正方形边长之间的关系,并通过相应的除法算式具体说明,让学生初步感知公因数的含义。(3)组织讨论还有哪些边长是整厘米的正方形纸片也能正好铺满,使学生明白:只有边长的厘米数既是12的因数,又是18的因数,才能正好铺满。(4)让学生再具体说一说 1、2、3、6 与12、18 的关系,由此得知:1、2、3、6 既是 12 的因数,又是18的因数,因而它们是12和18的公因数。(5)引导学生说说4为什么不是12和18的公因数,让学生在讨论中进一步完善对公因数的认识。
例题开发(改进原题):
(1)将长12厘米、18厘米的两条线段分成长度相等的若干份,各有几种分法。
________________12厘米
________________18厘米
(2)将长12厘米、18厘米的两条线段分成相同长度的线段,有几种分法。
教学思考:线段是一维的,而长方形有长和宽,是二维的。对学生来说,线段比长方形简单,将线段分成长度相等的若干份容易操作,这样改动,降低了学生的学习起点和操作难度,使学生可以更多地将注意力集中到对公因数的认识中来。通过问题(1),学生体会到了分成长度相等的线段的长度的厘米数应该分别是12的因数和18的因数。通过问题(2)将12厘米、18厘米的两条线段分成相同长度的线段,学生很容易想到等分线段长度的厘米数必须既是12的因数,又是18的因数,只能是1、2、3、6这四种,这时揭示公因数的概念,学生也比较容易理解。
原例题是让学生从正方形铺长方形的角度去理解公因数,既要考虑长方形的长,又要考虑长方形的宽,属于二维问题,思维起点较高,有相当一部分学生不能理解。改动后的两个问题,只要从线段的角度考虑即可,属于一维问题,学生比较容易理解。
二、优化数学活动,关注思维发展
教学的有效方式是数学活动,数学活动是思维的活动。有效的思维活动过程,既是师生、生生之间互动与交流的过程,又是教学流程的推进与学生认知活动的展开、契合、共振的过程。教师应关注学生的年龄和身心特征,对教学资源进行适度改编,以有效的活动促进学生思维的发展,实现数学知识与方法的有效迁移,提高课堂教学的有效性。
【案例2】苏教版教材小学数学第十册第六单元例2。

原题分析:本例题通过组织学生进行一些简单的操作活动,引导学生探索并发现圆的一些主要特征。例题首先给出了研究的方法和途径,让学生把任意画出的圆作为研究对象,采用折、画、比的方法展开探究。任意画的圆意味着每个学生手中的圆各不相同,这为得到一般性的结论奠定了基础,而折、画、比既是发现圆的特征的方法,也是验证圆的特征的手段。
例题开发(改进原题):
在刚才画圆的过程中,你发现圆的半径有怎样的特征?圆的直径又有怎样的特征?说说你的理由。
教学思考:教材上介绍了实物画圆、圆规画圆、绳笔画圆三种方法,三种方法如下图所示。

在圆规画圆、绳笔画圆两种方法中,学生观察并总结了两种方法的相同点:定点、定长。在此基础上,引出圆心、半径两个相关的概念。这两种画圆的方法中,绳笔画圆最能体现圆的本质特征——一中同长。
数学教学要力求让学生将已有的“日常生活经验”转化成真正的数学知识。而真正的数学知识不能只靠动手画一画、折一折、比一比、量一量来获得,还要借助活动经验展开数学的想象,由动手转向动脑,进而抽象归纳出相应的数学知识。在本节课中,我在画圆的基础上,让学生想象圆的半径的特征,同时进行一些简单的说理,并归纳出直径的特征。这些特征的得出完全可以借助在画圆的过程中定点、定长等经验得出。在得出这些结论后,再借助课前准备的圆形纸片,验证刚才分析的各个特征。总之,随着年级的升高,学生的思维会产生很大的变化,到了高年级阶段,学生既需要动手操作也需要动脑思考,两者相辅相成,这是我们二次开发教材时需要重点思考的。
三、设计问题串,构建知识体系
数学教材上的练习题,大多只是考查一两个知识点,而数学知识是前后联系比较大的一门学科,因此在平时教学中我们可以对其进行二次开发,将一些有着密切联系的知识点,开发成系列练习题,让学生在解决这些问题的过程中,理解数学,体会数学知识间的联系。
【案例3】苏教版教材小学数学第七册第三单元“整理与练习”第11题。
11.把下面两根彩带剪成同样长的短彩带且没有剩余,每根短彩带最长是多少厘米?

原题分析:本题是求最大公因数的应用问题,解决好此问题有三个关键的地方。(1)对“没有剩余”的理解:即短彩带的长度数必须是45的因数和30的因数。(2)对“同样长”的理解:短彩带的长度数是45和30的公因数;(3)对“最长”的理解:短彩带的长度数是45和30的最大公因数。理解了这三点,才可以很好地解决问题。教学时要逐步设问,让学生充分理解这三点,从而培养学生分析问题、解决问题的能力。
例题开发(改进原题):

有两根长分别为45厘米、30厘米的彩带。
(1)将45厘米的彩带剪成相同长度的短彩带且没有剩余,短彩带的长度分别是多少?有多少种不同的剪法?换成30厘米的彩带,情况又如何?
(2)将两个彩带剪成相同长度的短彩带且没有剩余,剪成后短彩带的长度分别是多少?有多少种不同的剪法?
(3)在所有的剪法中,最长的彩带长度是多少?
(4)最少可以剪成多少段?需要剪多少次?
教学思考:本题是关于求最大公因数的典型问题。关于最大公因数,有这样一条知识链:因数——公因数——最大公因数,知识链中的三个知识点是紧密联系的,同时这三个知识点的要求又是逐渐提高的。因数可以对于一个数而言的,而另外两个则是相对于两个以上的数而言的。在问题解决的过程中,如能将这些知识点进行串联,让学生对这些知识点进行比较,学生就能在比较中认识知识点的异同,同时体会知识生成的过程,从而加强对数学知识的理解,形成良好的知识结构。本题改动后,分别考查了如下的知识点:问题(1)考查了一个数的因数以及因数的个数;问题(2)考查了两个数的公因数以及公因数的个数;问题(3)考查了两个数的最大公因数;问题(4)是在(3)的基础上考查了“段数=长度÷每段的长度”这一数量关系,同时考查了“植树问题”这一数学模型。该问题串全面考查了一系列有着紧密联系的知识点,让学生在联系中加深对数学知识的理解,从而构建恰当、合理的数学知识结构。
总之,我们在平时的教学中,要做到合理使用教材,但又不局限于教材,要从学生、数学知识的角度,对教材进行二次开发,使教学更加贴近学生的学习水平,促进学生思维的发展。

