基于频响曲线稀疏表示的变压器绕组变形模式识别方法*
刘云鹏,程槐号,胡焕,张重远
(华北电力大学 河北省输变电设备安全防御重点实验室,河北 保定 071003)
0 引 言
电力变压器是供电系统中必不可少的设备之一,其健康的运行状态是供电系统具有安全可靠性的重要前提[1]。而变压器在运输中受到的碰撞、在运行中遭受的短路电流冲击及绝缘老化受损等各种情况都可能造成绕组不同程度的变形[2]。虽然早期的绕组变形缺陷一般不会导致重大事故,但是绕组的变形程度会随着设备的持续运行而逐渐加深,严重时可能就会造成变压器主绝缘击穿等后果。因此,提高电力变压器绕组状态监测水平对电网的安全运行有着重要的意义。
由于频率响应法(Frequency Response Analysis, FRA)[3]具有重复性好、灵敏度高等优点,因此现场常用FRA来诊断变压器绕组是否变形。但是该方法目前主要是应用于离线情况,存在检测不及时的不足。因此,国内外学者进行了许多关于利用FRA带电检测变压器绕组状态的研究,并提出了不少可行方案[4-7]。由于变压器频响曲线具有在线获取潜力,所以如果可以从变压器频响曲线中提取出可靠的特征值来实现变压器绕组变形故障分类,就能为变压器绕组的在线监测提供一种新思路。
信号稀疏表示是过去近20年来信号处理界一个非常引人关注的研究领域。其具有表达方式简洁、重构信号能力强等优点,目前已经普遍应用于图像去噪[8]、人脸识别[9]、信号识别[10-11]和非平稳信号分析[12]等诸多领域。但是将该理论应用于变压器频响曲线拟合及绕组变形模式识别中的研究目前尚未见报道。文中首次将稀疏表示理论应用于绕组频响曲线拟合及绕组变形模式识别中,提出了一种基于频响曲线稀疏表示的变压器绕组变形模式识别方法。该方法将频响曲线在Gabor原子的过完备原子库上进行稀疏拟合,然后从大量的匹配Gabor原子中提取出有效的特征向量,进而利用支持向量机实现基于稀疏分解结果的变压器绕组变形模式识别。最后还与采用频响曲线相关系数作为特征向量的模式识别试验结果进行了对比,验证了所提出方法的优越性。
1 稀疏表示及其匹配追踪算法
1.1 基本原理
稀疏表示的思想被引入到信号处理领域是近20年的事情,Coifman和Hauser[13]、Mallat和Zhang[14]等做出了重要的工作。1993年,Mallat和Zhang首次提出了应用匹配追踪(Matching Pursuit,MP)算法对信号进行稀疏分解的思想。匹配追踪算法是典型的贪婪算法,这种方法追求每次迭代的误差信号能量下降最大。其基本原理为:
假设待分解的信号为S,其长度为N;假定H为Hilbert空间,在这个空间H中,由一组已做归一化处理的向量{gq,q=1,2,…,Q} 构成一个集合H,并有Q>>N,则称集合D为过完备原子库,元素gq为其原子。基于MP算法的信号稀疏分解过程如下:
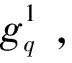
(1)
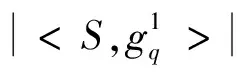
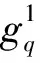
(2)
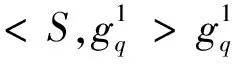
(3)
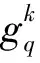
(4)
(5)
1.2 Gabor原子字典的构建及离散化
Mallat和Zhang提出匹配追踪算法时构造了一个包含了Gabor基、δ函数和复正弦基的过完备原子字典,称为Gabor字典。Gabor原子是一种广泛应用的原子,其数学表达式为:
(6)
式中g(t)=e-πt2为高斯窗函数;γ=(s,u,ξ)是原子参数;其中,s为尺度因子;u为位移因子;ξ为频率因子。
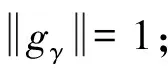
γ=(aj,pajΔu,ka-jΔξ)
(7)
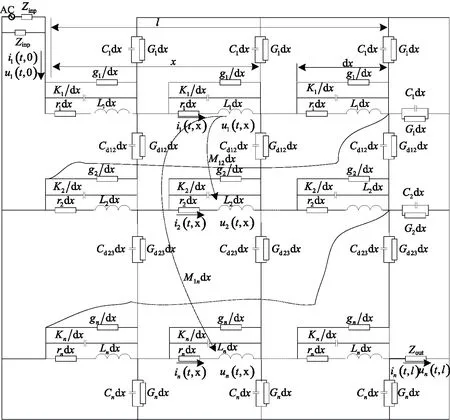
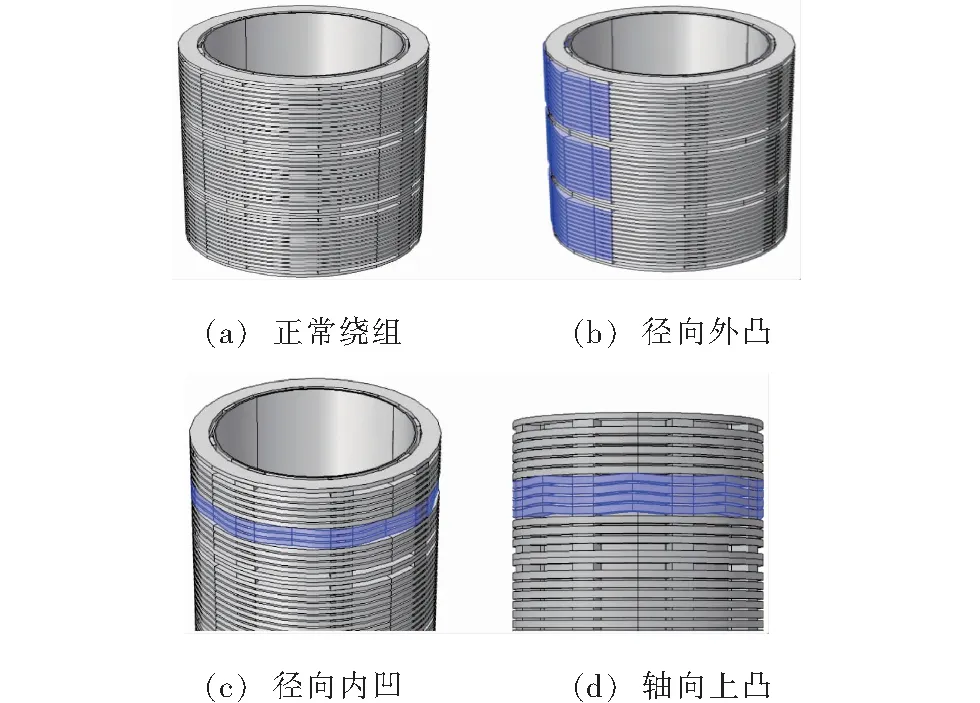
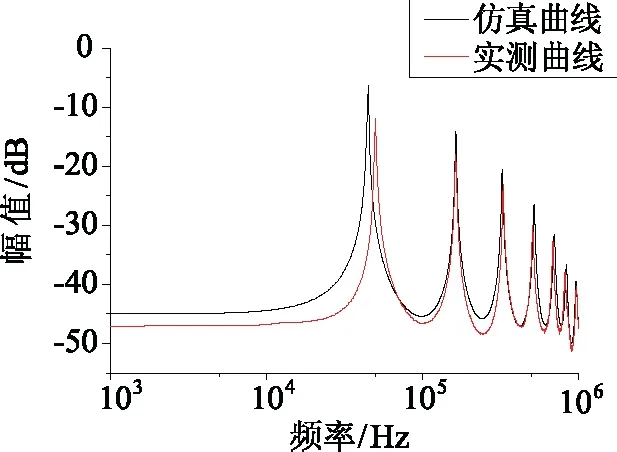
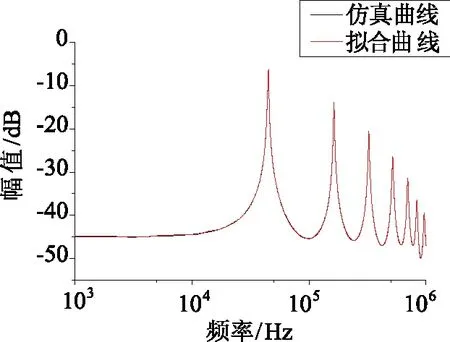
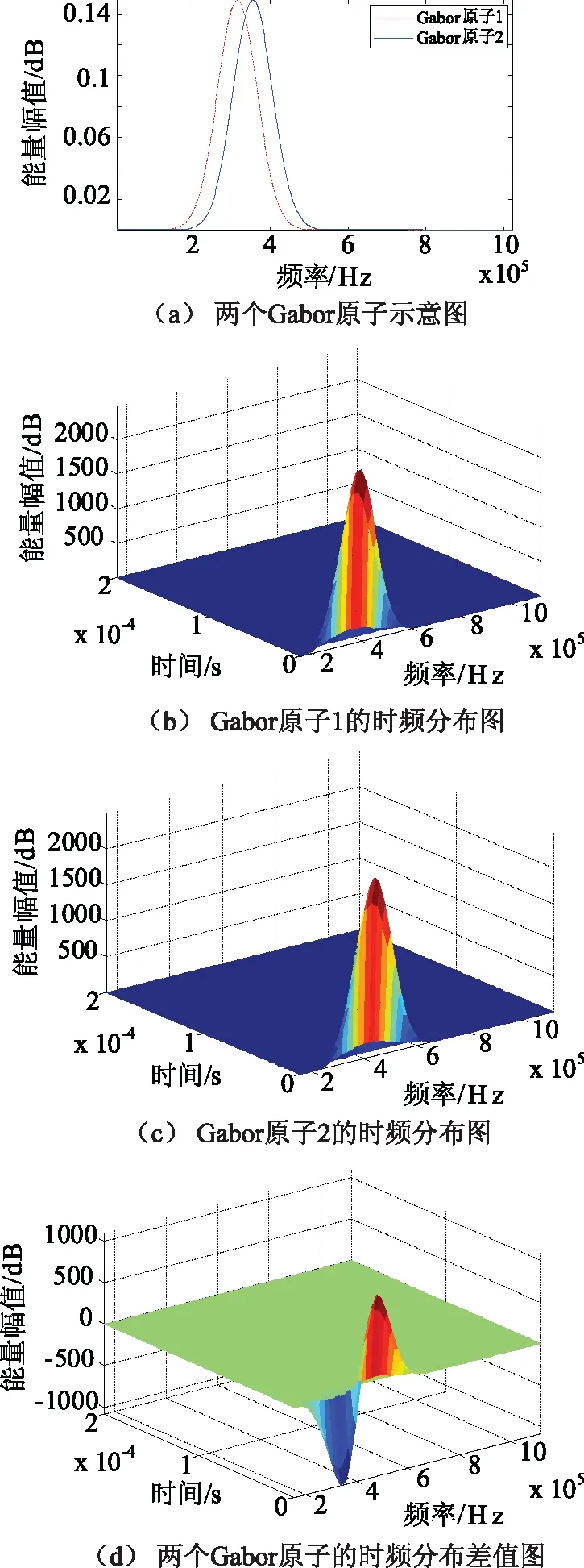
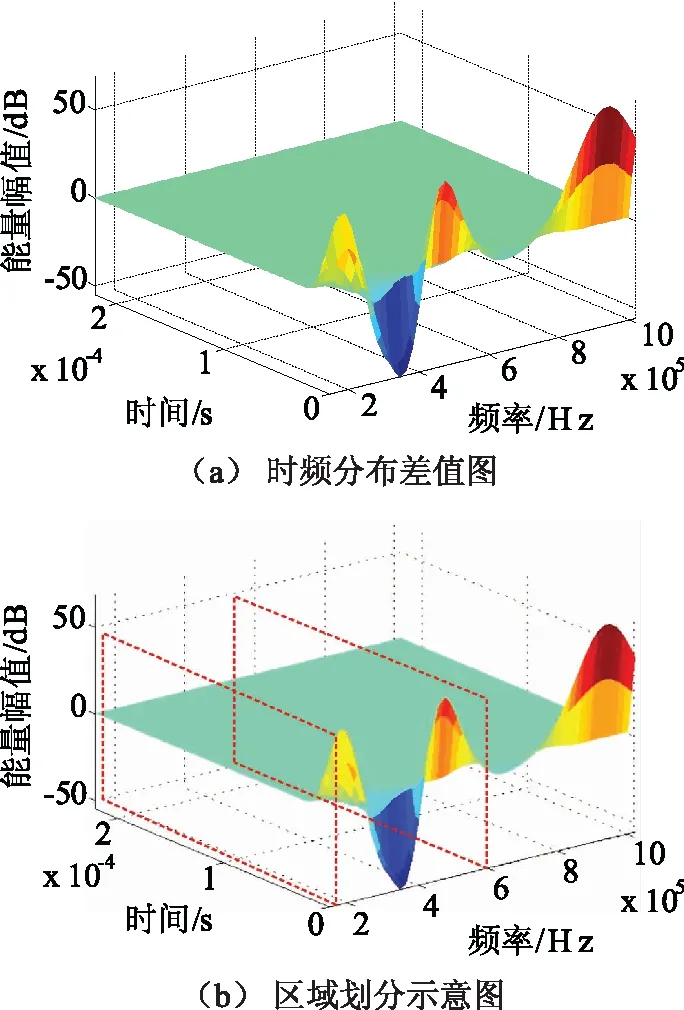
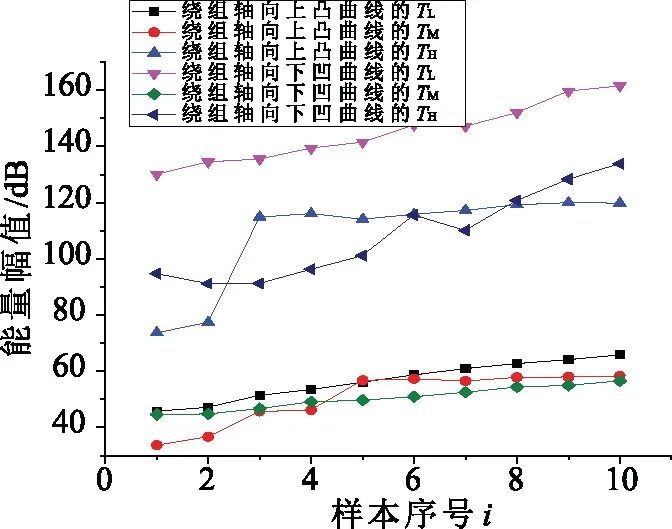
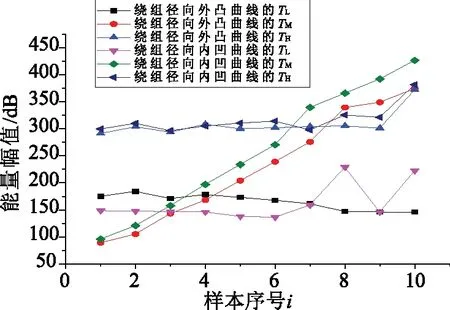
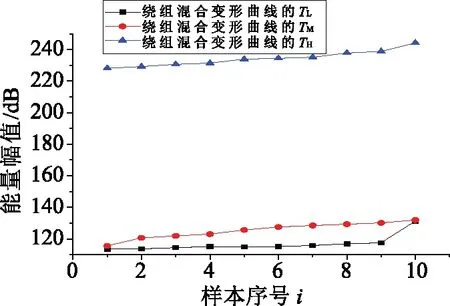
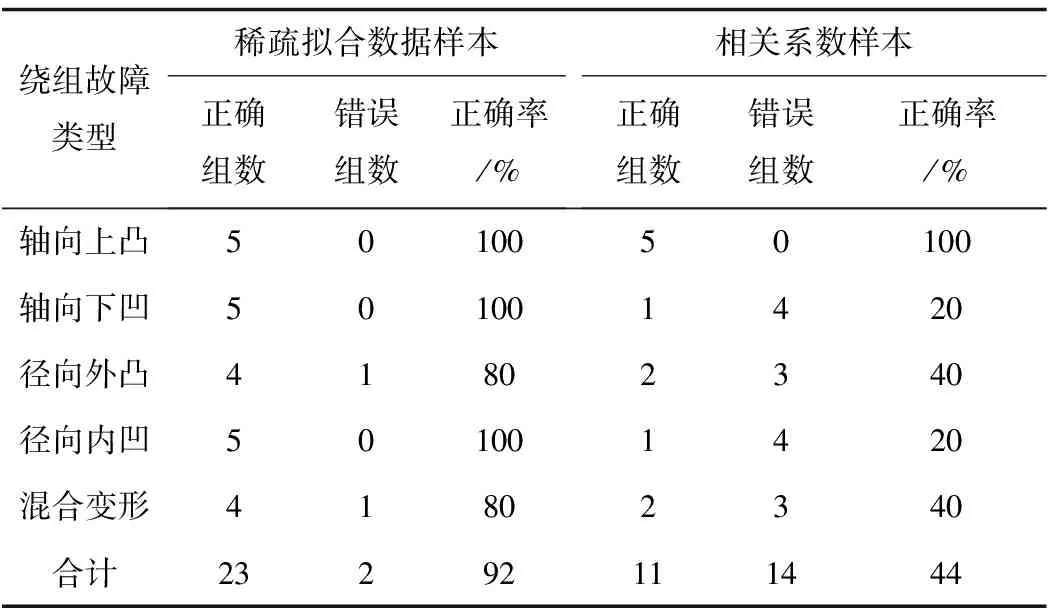
式中a=2;Δu=1/2;Δξ=π;0 图1给出了这种离散Gabor字典原子对空间的采样。由图1可以看出,随着倍频程值j的增加,位移参数u的扫描间隔变得越来越稀疏,而频率参数ξ的扫描间隔变得越来越密集。 图1 离散Gabor字典的空间采样 匹配追踪算法的本质是一种在局部寻找次最优解的贪婪算法。在迭代的每步,该算法致力于在给定原子字典中寻找与残留信号相对匹配的原子,保证算法的收敛。但是给定原子字典数目巨大,计算时间在这种条件下过长,这也是阻碍信号稀疏表示理论在实际中应用的一个关键因素。如果能够在一个相对较小的子字典中寻找与残差信号最匹配的原子,那么算法的计算复杂度将会显著减小。本文根据残差信号的特点构造了这种分解子字典。 (8) 基于离散自适应Gabor子字典的匹配追踪算法的具体步骤如下: (9) 式中IFFT(·)为傅里叶逆变换;Conj(·)为取共轭;FFT(RmS,N)可以直接利用第二步保存的结果。 (2)令Rm+1S=RmS- 匹配追踪算法有硬阈值法和软阈值法两种不同的终止条件。硬阈值法是指给定算法的迭代次数为K,只用K个Gabor原子的组合来表示原信号。这种方法的缺点就是K值不好确定,K值过大或过小都不能较好地表示原信号。软阈值法是指当残差信号的能量低于某一个阈值时终止算法。这种方法的缺点是,当信号信噪比较低时,残差信号能量可能会始终高于所设阈值,算法无法终止。 文献[16]给出了一种基于残差比的阈值终止条件,较好地减弱了噪声对阈值判定的影响。设RkS和Rk+1S分别为第k次和第k+1次的残差信号,则残差比q(RkS)为: (10) 文中以一个具有36饼,每饼10匝的变压器绕组为建模对象,通过结合多导体传输线模型和分布参数电路对该绕组进行了建模仿真。所用复合模型通过多导体传输线模型考虑了每饼中的匝间效应以提高模型的精度,再由所得传输线模型建立分布参数电路,如图2所示。 变压器绕组仿真电路的R、L、C等分布参数通过有限元软件COMSOL Multiphysics在静电场、磁场等多个物理场中进行求解[17-18],由此获取的参数较传统解析公式法更为精确。所研究的绕组变形类型包括绕组轴向上凸、绕组轴向下凹、绕组径向外凸、绕组径向内凹和绕组混合变形,正常及部分变形绕组仿真模型如图3所示。 图2 变压器绕组等效电路 图3 变压器绕组仿真模型 通过将正常绕组的实测与仿真频响曲线进行对比,验证了模型的有效性。曲线对比图如图4所示。 图4 实测频响曲线与仿真频响曲线对比图 利用信号稀疏表示理论拟合的绕组频响曲线如图5所示。由图5可以看出,拟合曲线具有很高的拟合精度,而且基于稀疏表示理论的拟合方法对于多峰值的频响曲线也可以实现全频段拟合,克服了传统拟合方法对于多峰值频响曲线需要分频段拟合的缺点。 图5 拟合频响曲线 由于支持向量机(SVM)特别适用于小样本数据的模式识别[19-20],而电力变压器绕组变形故障恰恰属于样本数量较少的类型,所以采用支持向量机模型对绕组变形故障类型进行识别。 支持向量机的主要思想是建立一个分类超平面作为决策曲面,使得两种不同类型数据之间的隔离边缘被最大化,从而区分不同类型的数据。对于样本数据线性可分的情况,SVM的最优分类超平面在原空间求取;对于样本数据线性不可分的情况,需要采用核函数Φ(·)映射的方法把样本转化到高维度空间中,转化后的样本是线性可分的,然后在这个高维度空间求取SVM的最优分类超平面。 最早的SVM算法只适用于二值分类问题,后来为了将SVM算法应用于多类问题,研究学者构造了SVM多类分类器。目前,最常用的SVM多类分类器构造方法有两种:一种是直接法,将多个分类面的待求参数整合到同一个目标函数中,通过求解该目标函数的最优化问题“一次性”实现多类分类。但是这种方法计算复杂,较难实现,一般只适合应用于小型问题;另一种是间接法,是通过组合多个二分类器来实现多分类器的构造,间接法主要又可分为以下两种: (1)一对多法:对于含有k个类别的训练样本,依次按照把某一类别的样本看做一类,剩余训练样本看做另一类的分类方法进行训练,这样就需要构造k个SVM。对未知样本进行分类时,取具有最大分类函数值的那一类为所求样本的类别; (2)一对一法:从含有k个类别的训练样本中任意选取其中两类样本构造一个SVM,那么k个类别的训练样本就要构造k(k-1)/2个SVM。利用该方法进行分类时,取得票最多的那一类为所求样本的类别。 可以实现SVM的工具箱有很多,文中采用的是台湾大学林智仁教授等设计的LIBSVM工具箱。这是一个操作简单、功能完善和能够快速实现SVM模式识别的软件包。使用LIBSVM可以轻松实现基于一对一算法的SVM多类模式识别。 要想实现基于频响曲线稀疏表示的变压器绕组变形故障模式识别,就必须要提出一个从大量的匹配Gabor原子中提取出特征向量的方法。提取特征向量的方法如下: 假设用于拟合某条频响曲线的匹配Gabor原子有N个。对每个Gabor原子按照式(11)进行短频傅里叶变换。 (11) 式中x(ω)是某个频域信号;W*(ω-ω0)是频域窗函数的共轭,随着ω0的改变,就可以得到频域信号x(ω)的时频分布。 需要说明的是,通过短频傅里叶变换得到的时域信息并无实际物理意义,作短频傅里叶变换的目的是得到Gabor原子的时频分布。之所以想要得到Gabor原子的时频分布,则是因为Gabor原子有很好的时频聚集特性,其时频分布具有较好的时频分辨率,能够灵敏地反映两条不同拟合频响曲线之间的细微变化。 图6(a)所示为两个形状相同,但位置有细微差别的Gabor原子;图6(b)及图6(c)为两个Gabor原子分别经过短频傅里叶变换后得到的时频分布图;图6(d)为两个Gabor原子时频分布的差值图。由图6可以看出,Gabor原子的时频分布差值图可以灵敏地反映出Gabor原子本身细微的变化。当变压器绕组发生变形故障时,其频响曲线的部分频段曲线也会发生相应变化,此时必然会导致拟合该频段曲线的Gabor原子发生改变,而这改变程度可以由Gabor原子的时频分布差值图得到。 图6 Gabor原子的时频分布 在分别得到N个匹配Gabor原子的时频分布后,再叠加N个原子的时频分布值就可以得到所拟合曲线的等效时频分布图,进而就可以获得正常绕组频响曲线与变形绕组频响曲线的时频分布差值图,如图7(a)所示。 由于绕组变形故障对频响曲线的影响仅会涉及到部分频段,所以为了提高特征值的灵敏度,按照国标DL/T 911-2016[21]中0~100 kHz为低频段,100 kHz~600 kHz为中频段,600 kHz~1 MHz为高频段的标准,将时频分布差值图分为三个区域,如图7(b)所示;然后分别求取各区域中数据点Z轴数值平方和的平方根作为反映低频段、中频段和高频段变形程度的指标TL、TM和TH。取绕组变形故障模式识别的特征向量为T=[TL,TM,TH]。 图7 频响曲线时频分布差值图 提出的基于频响曲线稀疏表示的变压器绕组变形模式识别方法的具体步骤如下: (1)在得到正常绕组频响曲线及各类变形绕组频响曲线的前提下,将所有频响曲线在过完备Gabor原子库上进行稀疏表示,得到各曲线的所有最优匹配Gabor原子; (2)对所有匹配的Gabor原子进行短频傅里叶变换,得到其时频分布值,然后分别叠加各曲线对应的最优匹配原子的时频分布值,得到各曲线的等效时频分布值; (3)计算正常绕组频响曲线与各类变形绕组频响曲线之间的时频分布差值,按上小节所述方法提取特征向量T=[TL,TM,TH],得到训练样本的特征向量集; (4)将样本特征向量集输入多分类SVM模型中,建立特征指纹库; (5)对待识别的绕组频响曲线进行同样处理,得到其特征向量T,并输入SVM模型中进行模式识别,最后得出诊断结果。 为了验证提出的变压器绕组变形模式识别方法的准确性,分别对正常绕组及不同变形情况绕组进行建模仿真,获取了绕组不同状态下的频响曲线,结合仿真曲线和交叉验证(Cross Validation,CV)方法进行了验证试验。 设置了绕组轴向上凸、绕组轴向下凹、绕组径向外凸、绕组径向内凹和绕组混合变形这5种故障类型,每种类型计算10组不同变形程度的数据,所以一共有50组样本。根据交叉验证法原理,每种故障类型选取其中的5组数据作为训练样本,剩下的5组作为检验样本。变压器绕组变形仿真曲线的特征向量样本值如图8~图10所示。 图8 绕组轴向上凸和下凹变形故障曲线样本值 图9 绕组径向外凸和内凹变形故障曲线样本值 图10 绕组混合变形故障曲线样本值 为了验证所提出的绕组变形模式识别方法的优越性,增加了以频响曲线低频段、中频段和高频段的相关系数为特征向量值的样本作为对比项。利用LIBSVM工具箱对训练样本进行归一化缩放、参数寻优和分类训练等处理,从而建立了基于稀疏拟合数据样本和基于相关系数样本的多分类SVM故障诊断模型。最后,分别将基于稀疏拟合数据的检验样本和基于相关系数的检验样本输入SVM故障诊断模型中进行了识别,结果如表1所示。 表1 多分类SVM模型分类结果 从表1可以看出,提出的绕组变形模式识别方法的准确率达到了92%,要明显高于以各频段相关系数为特征向量的模式识别方法。这说明基于时频分布差值的特征值比相关系数更能反映不同绕组变形故障下频响曲线的变化规律。至于其它变形故障的识别,只需要有新的训练样本输入到SVM模型中,通过训练形成新的分类器即可对其进行模式识别。 为了提高电力变压器绕组状态监测水平,提出了一种基于频率响应曲线稀疏表示的绕组变形模式识别方法。该方法将信号稀疏表示理论应用于绕组变形模式识别中,为绕组变形模式识别方法提供了一种新思路。 通过结合多导体传输线数学模型和分布参数电路模型对变压器绕组进行按饼建模仿真,得到了绕组在正常及不同变形故障情况下的频率响应曲线作为模式识别样本。针对电力变压器绕组变形故障样本属于小数据样本的特点,应用多分类SVM模型对经所提出方法处理后的样本进行了模式识别。试验结果表明,所提出的绕组变形模式识别方法的准确率高达92%。这验证了所提出方法的有效性,但是该方法在工程应用中的准确性还需大量的现场实验来验证。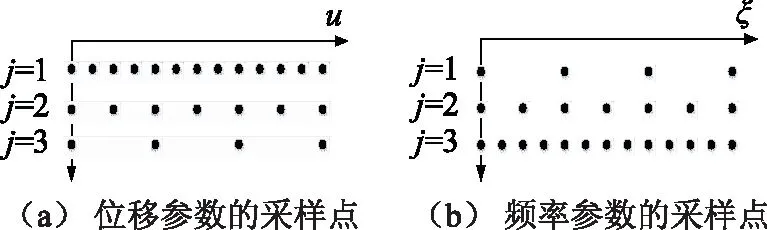
1.3 离散自适应Gabor子字典的匹配追踪算法
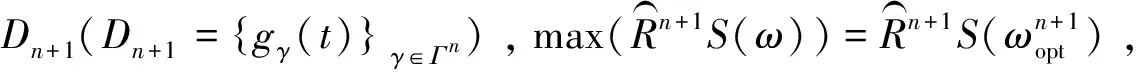
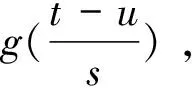
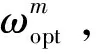
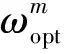
1.4 MP算法阈值终止条件
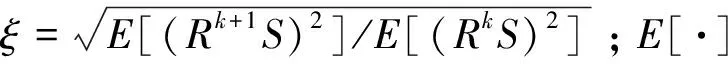
2 变压器绕组变形仿真及拟合曲线
2.1 变压器绕组变形仿真模型
2.2 基于信号稀疏表示的变压器绕组频响曲线拟合
3 基于频响曲线稀疏表示的模式识别实现方法
3.1 支持向量机的分类原理
3.2 基于稀疏分解信号的特征向量提取
3.3 基于稀疏分解的绕组变形模式识别方法步骤
4 试验结果与分析
5 结束语

