继电保护装置的一种新型评估方法*

徐岩，王士铭，刘婧妍，叶远波，谢民，黄太贵

(1.华北电力大学 新能源电力系统国家重点实验室，河北 保定 071003；2. 国网安徽省电力公司电力调度控制中心，合肥 230022)

0 引 言

随着我国智能电网的高速发展，计划检修制度已不能够满足电网安全稳定需求，状态检修成为一种发展趋势[1]。通过对正在运行设备的状态监测、分析和诊断，从而确定设备维修的工作内容和时间，相比于事后被动维修，状态检修不仅能够避免扩大事故产生的设备损失和停电损失，还能在一定程度上提高维修计划性[2]。与定期检修相比，状态检修根据装置状态制定检修策略，避免了多余的维修[3-5]。在确保电力系统运行安全稳定的前提下，经济效益也逐渐被放在了同等重要的地位，全生命周期成本(Life Cycle Cost，LCC)作为一种先进、科学的管理成本的理念逐渐应用于国内各大工程领域，华东电网从2003年启动了全寿命周期成本系列课题至今，已有较多基于输变电等大型一次设备的LCC研究模式，通过实际管理获得成功[6]。但是目前针对继电保护装置将状态监测与LCC管理相结合依据经济效益推算出其剩余寿命的研究尚不多见，因此，该方面的研究有待于进一步开展。

文献[7]根据保护系统状态检修所需的可靠性指标，利用Markov模型评估系统在给定条件下的检修需求，但并未考虑到可靠性与寿命的关系；文献[8]提出一种采用粒子群优化模糊神经网络的变电站LCC估算模型，根据前期投资成本及同类型设备的经验参数进行总成本估算，未能体现出设备个体差异性；文献[9-10]提出电力变压器的经济寿命评估模型，通过比较检修与更换设备下的年均最大收益值，做出适用决策；文献[11]根据历史故障率记录数据并基于Marquardt法构建了设备失效模型，分析了继电保护装置生命周期成本各项因素，由于当时状态监测发展尚不完善，导致其故障率数据信息不具有时效性，且失效样本数据较少，所得出的故障率模型难免出现较大误差。

文中首先基于状态评价数据的继电保护实际故障率模型，建立保护状态量与实际故障率之间的关系；其次通过优化极大似然法拟合继电保护装置随役龄变化的失效率曲线，符合Weibull分布函数；最后以全生命周期成本理论为依据，构建继电保护装置全寿命周期内日平均成本模型，当成本费用最小时为最佳退出役龄。

1 基于健康指数的设备可靠性分析

由文献[11]所得故障率，是建立在从保护装置投运一直到退役，期间对装置的实际运行状况进行记录，并针对故障次数综合统计所得到的，鉴于我国电力系统一直以安全运行为基本出发点，且设备更新换代速度较快，运行中发生失效的保护装置样本很少，用这种方法得到的失效率相对目前来说精度较低。并且此方法是基于故障发生后对样本进行统计分析，并不适用于目前状态检修的大环境。目前的研究成果指出，健康指数与装置的故障率之间所符合的函数关系，并不止适用于输变电等一次设备，继电保护装置也同样适用。

1.1 继电保护装置状态评价内容

继电保护装置的健康指数HI(Healh Index)是用来描述设备状态的劣化程度。任意一台保护设备通常都是由多个部件组成，每个部件均由若干个状态量共同决定，因此，设备的基础状态量的采集变得十分必要。离线试验技术又称预防性实验，需要定期在设备停役时进行实验，状态评价的结果往往不能反映当前设备运行的真实状态。带电检测和在线监测是目前掌握设备实时状态的关键技术，目前成熟的方法有紫外电晕检测、红外检测测、局部放电检测等。在线监测是基于智能变电站，通过连续检测特征量进而提取出部件的状态量，使基础数据更加准确，更加具有时效性[12]。

参考IEC 62059《电测量设备-可信性》，其中第21部分描述关于使用抽样检验和现场失效报告来进行失效数据的分析整理的方法。主要从以下四个分类中收集数据：装置复杂性定义；失效的分类；从故障装置中；抽样方案。

国网公司于2015年颁布了继电保护状态评价导则(Q/GDW 11285—2014)，针对继电保护的保护装置本体及二次回路规定了具体评分标准(如表1所示)，结合实际电力公司附加评价量及权重分值便可计算出设备健康指数。

表1 继电保护状态评价量及分值

1.2 健康指数与当前状态的故障率推导

老化健康指数是指继电保护装置在当前运行的情况下，依据老化原理计算得来的理论老化值，随着役龄增加，继电保护装置的健康状态下降，依据设备的老化原理，总结出式(1)来描述设备状态随时间变化：

HIa=HIa0×eB(T2-T1)

(1)

(2)

式中HIa是老化健康指数；HIa0是区域内老化健康指数的投运时的初始平均值；B为老化系数；Ti为新设备投运年份；T2为所要计算老化健康指数的年份。

研究表明，设备的健康指数与实际故障率之间存在如下关系：

λ=K·eC·HI

(3)

式中λ设备故障率；K为比例系数；C为曲率系数；HI为继电保护装置的健康指数，数值范围为(0～100)。按照文献[13]的分类统计方法，每10分为一个等级，将健康指数一共分为十级，当样本数据较少时，可利用至少两年的设备健康指数和设备平均故障率数据代入式(4)进行反演计算获取比例系数K值和曲率系数C值，K=86.39，C=-0.160 1。

(4)

式中P为保护装置年平均故障概率；i为健康指数区间分类，i=1～10；Ni为第i个健康指数区间保护装置总台数；HIi为对应分类的HI平均值。当K、C值确定后，即可由式(3)求得基于设备健康状态的实际故障率[14]。

1.3 加速寿命试验

按照IEC 62059可信性标准，其中可靠性加速试验作为一种较为实用的方法在实验室中得到了广泛的应用。相较于常规寿命试验耗时久、耗资大的缺点，它在不引入新的失效机理前提下采用加大应力的方法使得样品在短时间内失效，达到预测设备在正常情况下的寿命的效果。但实际运行中不可预测因素较多，难以作为寿命评估的最终依据。

但是可靠性加速试验可以使装置缺陷提早出现，指导其在投入使用前消除固有设计缺陷，从而提高装置的可靠性及耐久度。

2 基于Weibull分布的失效率模型

2.1 浴盆曲线

工程实践表明，保护装置和一般的工业产品类似，故障率会随时间的推移而改变，其失效率符合“浴盆曲线”的特性，如图1所示。

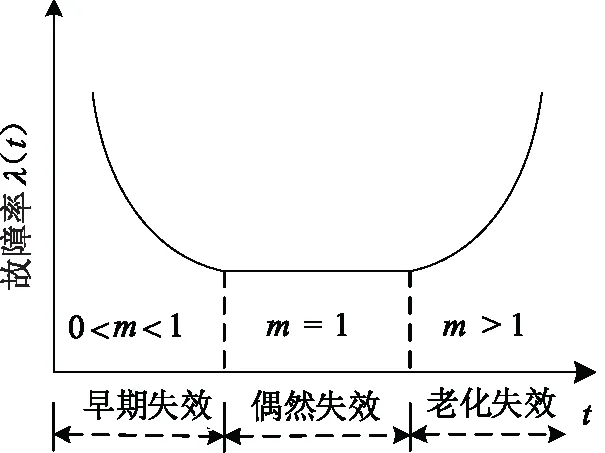
图1 装置浴盆曲线

浴盆曲线按早期失效期、偶然失效期、老化失效期分为三段。初期装置失效率较高并随着工作时间迅速下降，其原因在于产品设计与制造的缺陷，按照要求，一般制造商对未出厂的产品要进行厂内测试及“火烧”等工艺来及时发现并度过早期失效期之后才交付使用。偶然失效是指由于外界环境因素如雷击、信号干扰等引起保护装置故障，通常情况下，偶然失效率较低并可以近似地看做一个常数。老化失效期又称损耗失效期，随着元器件老化、磨损，故障率随设备役龄急剧增加，此时老化失效率占绝对主导地位。

2.2 Weibull分布失效率曲线

在工程应用中，常用的设备故障分布形式有指数分布、正态分布、伽玛分布以及Weibull分布等，其中指数分布和Weibull分布最为广泛。对于保护设备来说，Weibull分布具有形状参数β，可以全面描述浴盆曲线的三个阶段，符合设备全寿命阶段变化。因此，本节采用二参数Weibull分布函数拟合保护装置故障率曲线。

二参数Weibull分布的可靠性分布函数为[15]：

(5)

故障密度函数为：

(6)

-ln(1-F(t))=λt

(7)

式中t取值均≥0；m为形状参数；γ为尺度函数；F(t)为故障累计分布函数。

故障率函数为：

(8)

当01时，失效率随时间逐渐递增，函数为正指数的幂函数，是典型的损耗效应，可以用来模拟设备老化、部件磨损等。

估计模型参数前，需要对统计样本进行适当的前期处理，尽量选择设计相同，运行环境相似的保护装置，有助于排除其他不定因素。最小二乘法法具有精度高、拟合较为贴近的优点，因此，采用该方法对模型中参数进行估算。

3 继电保护装置全寿命周期成本

3.1 LCC构成

全寿命周期成本1904年萌芽于瑞典铁路系统，后在国防建设，航空行业中逐渐被利用，创造了巨大的经济价值。20世纪80年代，国际电工委员会颁布了《全寿命周期费用评价》标准，电力行业通常将其划分为：初始投入成本CI，运行成本Co，检修成本CM，故障成本CF和退出成本CD。根据保护装置实际运行情况，考虑设备互联将对整个系统影响所产生的成本，对其进一步分解，得到LCC的详细构成，如图2所示[16]。

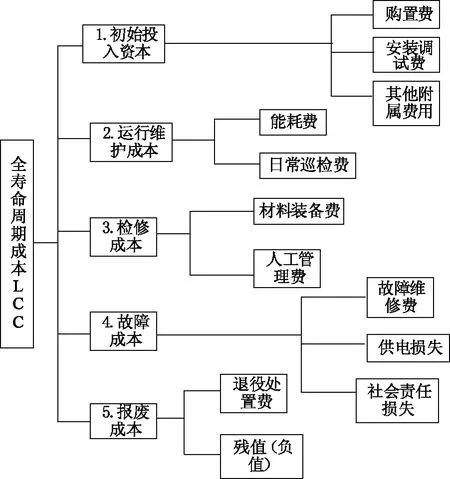
图2 保护装置LCC

LCC计算可表示为：

LCC=CI+CO+CM+CF+CD

(9)

(1)初始投入资本CI

投资成本CI是指在保护装置投运之前，在工程建设与安装调试期间所花费的总费用。主要包括设备购置成本、安装调试费用和其他与系统相关的附属成本，如研究设计费、培训费等。对于继电保护装置来说，安置空间较小，因此便不考虑土地购置等成本。此类成本为固定成本，不会随时间及故障率变化而变化，可以直接获取且计算较为简单。

(2)运行维护成本CO

运行维护成本指的是保护装置日常运行产生的费用，包括能耗费、日常巡视检查费等其他费用。常规巡视主要是指工作人员按照计划进入现场对装置巡视及时发现故障，其中人工管理、材料消耗是主要的成本所在。二次设备能耗费用一般只包括损耗的电费，年损耗费可视为基本不变。因此我们假设随着保护装置运行役龄的增加，年度例行运行维护成本采用以下估算模型：

CO=100T

(10)

(3)检修成本CM

对于可修复的设备来说，当出现故障时，要有相关工作人员对故障设备进行计划维修。目前数字化继电保护装置一般均由插件组成，通过更换故障插件即可完成检修目的。因此检修成本指的是保护装置在检修时所需材料、配件、装备、人工、管理等成本失费用的总和。因为是计划检修，便不考虑因为停电造成的风险成本。同样，我们这里假设随着保护装置的役龄增加，检修成本线性增加。

(11)

式中CMb为单次检修的基本费用，基于变电站长期经验积累获得数据。

利用目前状态检修的成果及故障率曲线估算出检修次数，从而取代之前周期性检修所计算的固定次数费用，随着设备役龄的延长，设备失效率逐渐升高，导致相对应的检修成本也会逐渐增加。

(4)故障成本CF

故障成本也可看作是一种事故风险惩罚成本，保护装置作为电力系统中的重要设备，一旦发生故障势必会对供电可靠性造成影响，使系统无法正常运行，由此可能造成的直接和间接经济损失，包括供电损失、故障修复费用以及相应的社会责任损失费用等。文中为方便而不失一般性地反映缺点影响，同时考虑可靠性的影响，构造一种断供成本的估算方法：

CF=POTF×LOTF

(12)

式中CF指的是保护装置的风险值，单位是元；POTF是变压器的故障发生概率；LOTF是变压器发生故障后的经济损失。文中LOTF主要包括发生故障情况下系统停止供电造成的系统缺损失及用户缺电损失。

LOTF=(e+c)EENS

(13)

式中EENS—可靠性指标电量不足期望值，它指的是研究时间段内由于电网供电不足造成用户减少用电量的期望值；e为单位电价；c为用户缺电单位损失[17]。

(14)

(5)报废成本CD

报废成本包括设备退出运行时报废处理成本和残值，处置成本指保护装置报废后拆除和运输及人工成本；残值指的是保护装置报废后可回收利用的费用，属于可收入型成本。

CD=CD T-CD R

(15)

式中CD为报废成本；CDT为退役处置费；CDR为设备退役时的残值；一般根据经验来说，退役处理费按照设备安装直接工程费的32%计算，由于保护装置为材料密集型产品，其中含有较多的金属材料，因此按照设备购置费的5%进行计算。

3.2 模型搭建

经过上述分析得知，成本中一共分为两类，一类是随役龄增长故障率的上升导致成本不断升高，另一类则是与故障率无关的成本包括初始投资成本，运行成本，退役处置费和残值，运行成本作为可变成本，随着运行时间的延长，其成本不断增加，但同时平均至每一天时成本也会不断变化。假设到第T天的时候设备退出运行，所得出的平均成本模型如下：

(16)

4 算例分析

4.1保护装置失效率估算

以安徽某110 kV数字变电站为例，对其役龄内全部数据进行汇总，根据平时对装置的健康状态评估得出设备健康指数，按照式(3)计算可得出以其役龄为时间的实际故障率，记录如表2所示。

依据表2中实际故障率数据，采用最小二乘法法估计Weibull分布函数中的未知参数；m=5.847，γ=4 679。因此，根据日常监测所得偶然故障率为1.74×10-5可知，保护装置的实际失效率模型为：

(17)

表2 健康指数及实际故障率

故障率曲线分布如图3所示。

图3 保护装置故障率曲线

4.2 经济寿命预测

以该变电站中的某保护装置为例，根据运行经验所得各部分经济指标如表3所示。

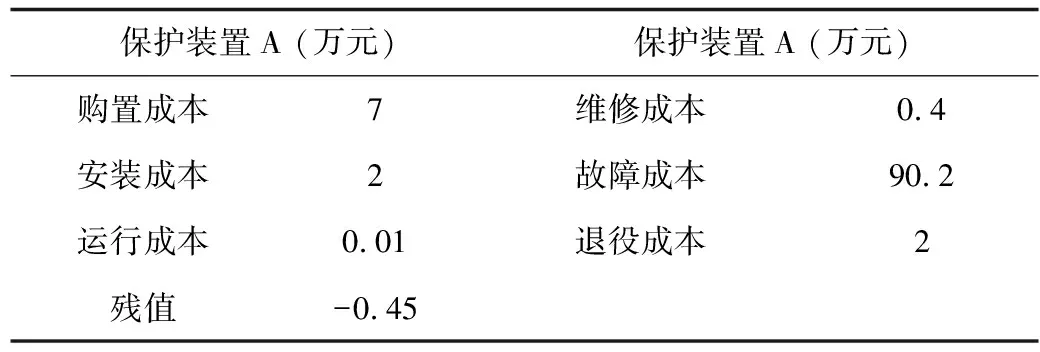
表3 保护装置经济指标

根据以上基本数据，将其代入到式(16)的模型中进行计算，通过Matlab进行仿真可以得到保护装置日平均成本值见图4。

由图可知，在投运初期的时候，装置处于偶然失效期，很少发生故障事件，因此其投资成本对曲线起到了决定性作用，日平均成本随着运行时间逐渐下降；此后，随着装置役龄增长，老化现象逐渐显露，故障率呈指数上升，与其相关的维修和故障成本快速升高，而其投资成本已经很低，所以总平均成本呈增大的趋势。使得保护装置平均成本曲线最低点出现在第2 470天左右，所对应的成本费用为167.47元。

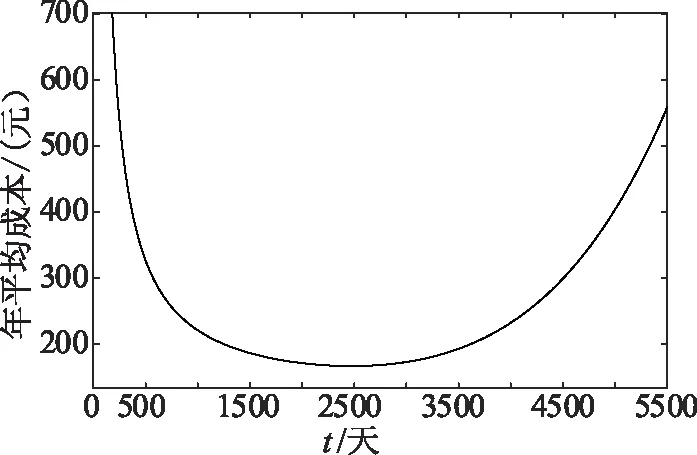
图4 装置日平均消耗变化曲线

根据前面的分析，故障率是装置经济寿命的决定性因素，若是保护装置在日后能维持一个较低的故障流程水平，其最佳经济寿命便可以延后；若按现状发展，则在第2 470天时退役较为合适。对比于当今的主流退役模式，其具有更大的灵活性。

5 结束语

在将新的故障率算法应用于全生命周期成本理论的计算，搭建了继电保护装置经济寿命评估预测模型，该方法通过分析装置随运行时间的增加其日平均成本的变化来预测装置的最佳退出运行的时间。通过引入健康指数的概念，并依据《继电保护状态评价导则》进行评分，通过计算得出装置的实际故障率。以110 kV变电站为例，考虑其各项的成本因素得出的平均成本模型曲线先快速下降到达一段平稳期，随着故障率的提高曲线呈上升趋势，可以得到日平均成本最低的时间点，验证了所建立的经济寿命评估模型对实际装置的运行规划具有指导意义。此外，本模型依据经济效益所得出的装置最佳退役时间也可以作为状态检修的决策手段之一，具有发展意义。