基于混合H2/H∞控制理论的交直流并联系统机网阻尼协调控制*

张爽，曾雪洋，摆存曦，田蓓，李保宏，刘天琪

(1. 国网宁夏电力有限公司电力科学研究院，银川 750001； 2.四川大学 电气信息学院，成都 610065)

0 引 言

如今，我国已经形成了大规模跨区域交直流混联的复杂电网，电网建设过渡期，“强直弱交”特征明显[1-3]，交直流系统相互影响严重，区域间低频振荡现象逐渐增多[4-5]。电力系统稳定器(PSS)和高压直流输电(High Voltage Direct Current，HVDC)附加阻尼控制器均可以有效地抑制电力系统低频振荡[6-11]，文献[6]考虑PSS的相位补偿特性和幅频特性，提出了抑制共振机理低频振荡的方法。文献[7]分析了有功型 PSS抑制低频振荡的机理，文献[8]基于鲁棒控制理论设计了孤岛运行方式下用于同时抑制低频振荡和次同步振荡的多通道HVDC鲁棒控制器，文献[9]提出一种计及时延的互联电力系统分散式阻尼控制策略。以上文献仅单独采用PSS或HVDC的附加阻尼控制器抑制低频振荡，均没有统一协调二者。虽然文献[10]基于线性最优控制理论提出了一种PSS与HVDC协调的交直流低频振荡附加阻尼控制器，但PSS主要用于抑制区域内的低频振荡，并且也没有和传统附加阻尼控制器进行对比。文献[11]提出了一种基于ERGA和混合H2/H∞方法的交直流并联系统的分散控制方法，但发电机附加阻尼控制也主要用于抑制区域内部振荡。

提出一种基于混合H2/H∞控制方法的交直流并联电网机网阻尼协调控制策略，首先采用最小二乘-旋转不变(TLS-ESPRIT)算法辨识出系统振荡模式和开环降阶传递函数模型，结合混合H2/H∞控制方法在HVDC和发电机励磁中设计附加阻尼鲁棒控制器，最后在PSCAD/EMTDC中搭建仿真算例，并与传统附加阻尼控制器对比，仿真结果验证了附加鲁棒阻尼控制器抑制区域间低频振荡的准确性、有效性。

1 混合H2/H∞控制理论

交直流电网的状态方程和输出方程可以描述为：

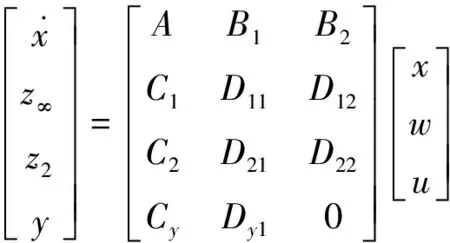
(1)

式中x为状态向量；u为控制信号；w为外部干扰；y为观测信号；A、B1、B2、C1、C2、Cy、D11、D12、D21、D22、Dy1均为状态方程的参数矩阵；以z∞衡量控制器的鲁棒性；z2衡量控制器的输出代价。

输出反馈控制器K(s)可写为状态空间方程形式：

(2)

式中η为控制器的状态；AK、BK、CK和DK为控制器的参数矩阵。

联立式(1)和式(2)，消去变量u和y，可得原系统和控制器组成的闭环系统为：

(3)

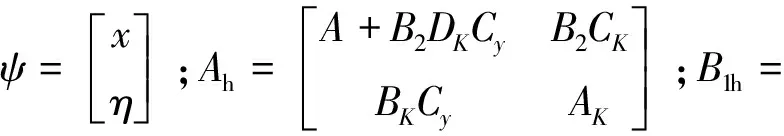
标准的H2/H∞控制问题如图1所示[8,12]。其中，G(s)为被控系统；W1(s)、W2(s)、W3(s)为加权函数；z∞=[z∞1z2]T。

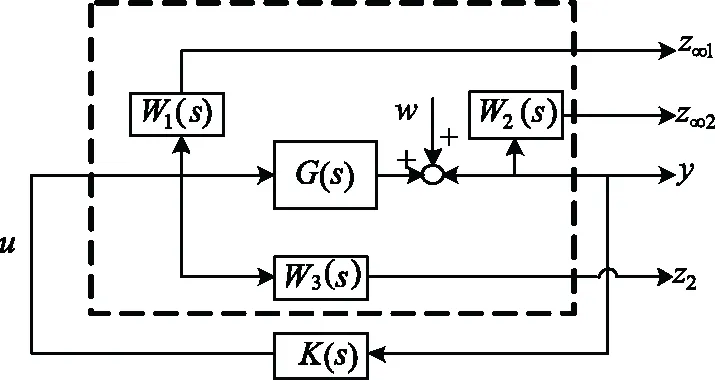
图1 H2/H∞控制问题

定义Twz∞为从w到z∞的闭环传递函数；Twz2为从w到z∞的闭环传递函数。那么，控制器K(s)设计条件如下：

若Ah稳定，即当且仅当存在对称正定矩阵X1，使得：

(4)

若Ah稳定，即当且仅当存在对称矩阵X2>0及Q，使得：

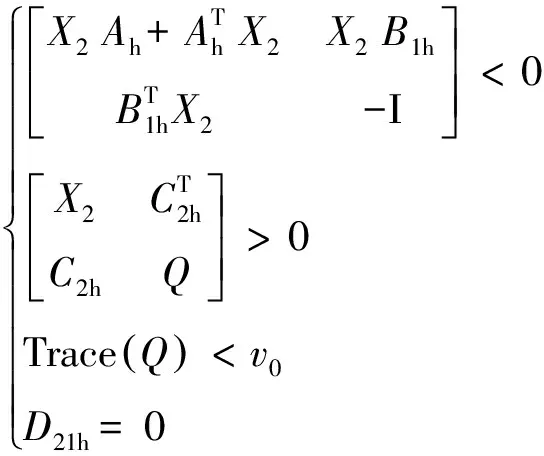
(5)

(3)闭环系统极点位于某一给定的线性矩阵不等式(Linear Matrix Inequalities，LMI)区域D，并且满足如下性能指标：

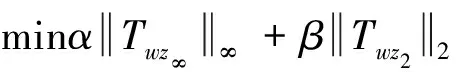
(6)

条件(1)可保证闭环系统对由w=Δ进入的不确定性具有鲁棒性；条件(2)保证用H2范数度量的系统性能较好(如：噪声输入w，z2具有较小的稳态方差；脉冲输入w，z2具有较小的能量)；条件(3)则通过将系统极点限制在复平面上的一个恰当区域中，使阻尼比和振荡频率满足给定的界限，保证其具有期望的过度过程特性。

LMI区域定义为：

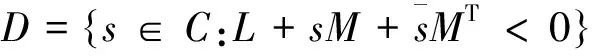
(7)

式中L=LT，M为确定的实数矩阵。当且仅当某些包含Ah的线性矩阵不等式可解时，矩阵Ah的全部特征值位于LMI区域D。区域D具有多种类型，其中比较典型为如图2所示的阻尼比ξ大于cosθ的锥形区域[8,12]。

图2 极点配置区域D

为满足上述条件，并便于计算处理，需强制X1=X2=X3，从而基于线性矩阵不等式法联立求解式(4)～式(7)构成的不等式组。

2 附加鲁棒控制器设计

2.1 系统模型

在PSCAD/EMTDC中搭建如图3所示的四机两区域仿真系统。图3中，区域1和区域2之间由双回交流与单回直流并联连接，其中HVDC整流侧定直流电流控制、逆变侧定熄弧角控制，HVDC传输有功功率为Pdc=198 MW，交流通道输送功率Pac=209 MW。四台发电机都为汽轮机，均装有调速器、励磁器，仅发电机G2装有PSS1A型PSS，其余三机未装PSS。区域1的负荷PL1=302 MW，区域2的负荷PL2=556 MW。

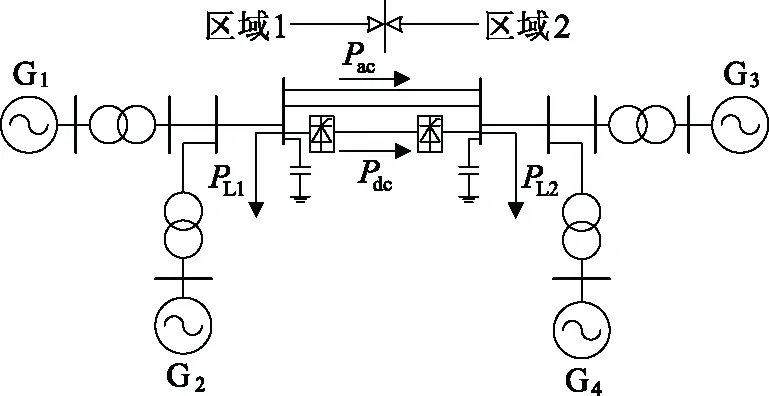
图3 四机两区域系统模型

2.2 TLS-ESPRIT振荡模式辨识

TLS-ESPRIT算法是一种基于子空间技术的高分辨率信号参数估计方法，在电力系统的谐波检测、暂态信号分解、分布式电源解列等场合得到广泛应用[10-13]。与传统的Prony算法相比，它具有更强的抗干扰、抗噪能力和更高的计算效率，适用于对系统输入输出间的传递函数模型辨识[10-16]。

对图3所示的四机两区域系统采用TLS-ESPRIT算法辨识系统的振荡模式。取发电机G1为激励点时，辨识得到区域1与区域2之间存在0.72 Hz阻尼比为4.31%的区域间低频振荡模式；取发电机G3为激励点时，辨识得到区域1与区域2之间存在0.72 Hz阻尼比为4.28%的域间低频振荡模式。因此可以在HVDC整流侧定电流控制和发电机励磁中设计附加鲁棒阻尼控制以抑制区域间的低频振荡。

2.3 HVDC附加鲁棒阻尼控制器

(8)

结合混合H2/H∞控制理论，设计出HVDC附加鲁棒阻尼控制器，如图4所示。

图1中的加权函数确定为：

(9)

(10)

W3(s)=10

(11)

设置式(6)中的α=β=0.5，基于线性矩阵不等式法联立求解式(4)～式(7)构成的不等式组，便可以得到控制器。为满足工程实际，采用平衡截断法降阶，降阶后的附加鲁棒阻尼控制器为：

图4 HVDC附加鲁棒阻尼控制器

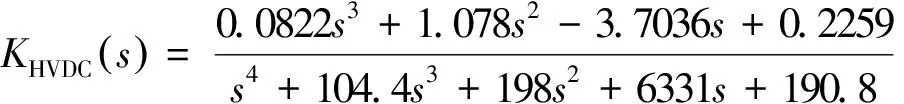
(12)

图5为HVDC引入附加鲁棒阻尼控制器KHVDC(s)前后辨识得到系统振荡特性。由图5可知引入附加鲁棒阻尼控制器后，系统的振荡特性明显改善。

HVDC安装附加鲁棒阻尼控制器后，在发电机G3励磁系统施加阶跃扰动，以发电机G3和G1转子角速度的偏差Δω31为输出，Δω31经带通滤波器后，基于TLS-ESPRIT算法辨识得到开环传递函数GG3(s)，如式(13)所示。其中带通滤波器为高通滤波器，即：

10s/1+10s。

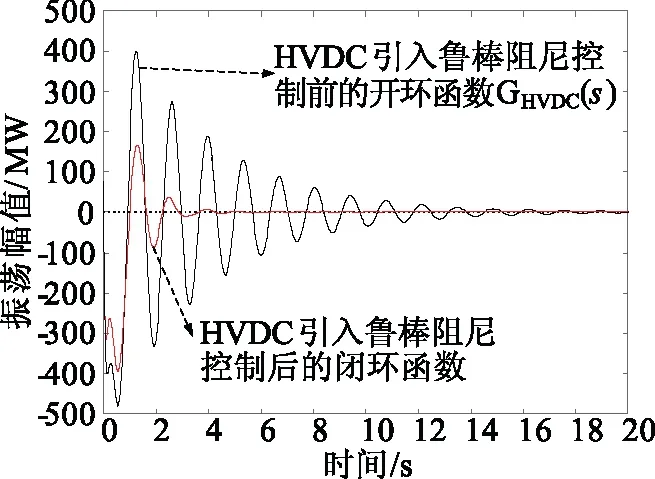
图5 HVDC引入反馈前后系统振荡特性

2.4 发电机附加鲁棒阻尼控制器

为进一步提高交直流输电系统稳定性，抑制区域间低频振荡，使用HVDC鲁棒控制器设计方法，设计发电机励磁附加鲁棒阻尼控制器，以协调2.3节设计的HVDC附加鲁棒阻尼控制器，实现机网阻尼协调控制。

(13)

参照HVDC附加鲁棒阻尼控制器的设计方法，令α=β=0.5，设计出如图6所示的发电机G3附加鲁棒阻尼控制器。

图6 发电机G3附加鲁棒阻尼控制器

加权函数确定为：

(14)

(15)

W3(s)=10-5

(16)

采用平衡截断法降阶，得到发电机G3附加鲁棒阻尼控制器KG3(s)：

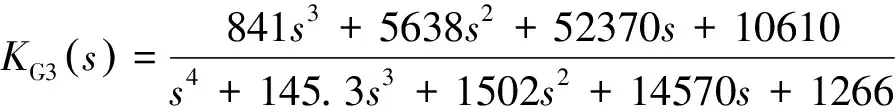
(17)

图7为发电机G3引入附加鲁棒阻尼控制KG3(s)前后，辨识得到系统振荡特性。由图6可知引入鲁棒控制环节后，系统的振荡特性明显改善。

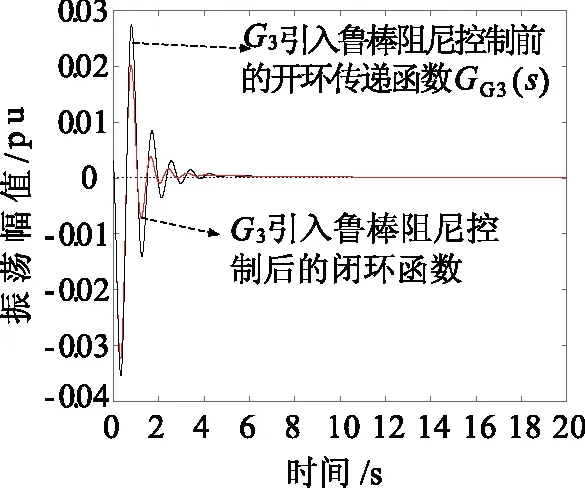
图7 G3引入反馈前后系统振荡特性

3 时域仿真分析

3.1 传统控制

为对比附加鲁棒阻尼控制器的控制效果，将其与传统附加阻尼控制器对比，其中传统附加阻尼控制器参考美国太平洋直流经典的附加直流阻尼控制器和IEEE的PSS1A设计，其结构和参数如图8和图9所示[11]。

图8 直流传统附加阻尼控制器

图9 发电机G3的PSS

3.2 直流鲁棒附加控制器验证

在图2所示的四机两区域仿真模型中施加如下的两种扰动方式：t=3 s时HVDC受到一个扰动，整流侧定电流控制的电流参考值由1 p.u增加至1.02 p.u；t=3 s时，区域2发电机G4的高压母线侧发生三相金属短路接地故障，接地电阻0.01 Ω，3.1 s故障清除。

以交流线路输送有功功率Pac和发电机G3与G1转子角速度偏差Δω31为评价指标，两种扰动下的仿真结果如图10所示。

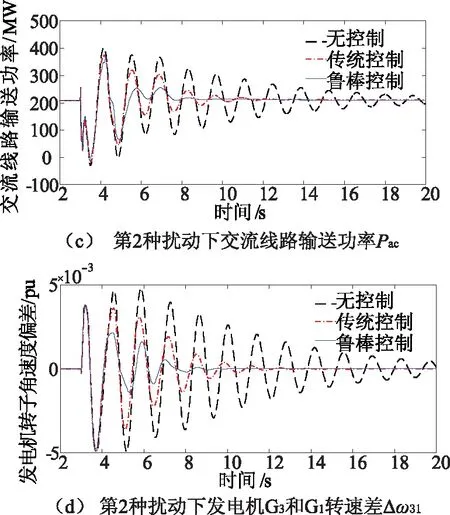
图10 直流传统控制与鲁棒控制的控制效果对比图

从图10可知，不同的扰动方式下，与无附加控制相比，HVDC传统附加阻尼控制能够抑制区域间的低频振荡，降低首摆幅度，增加后续摆动的阻尼，而文中的HVDC附加鲁棒阻尼控制器，降低首摆幅度和增加后续摆的阻尼明显优于传统附加阻尼控制，系统恢复稳定运行的速度更快，鲁棒性更强。

3.3 发电机励磁鲁棒附加控制器验证

在HVDC安装附加鲁棒阻尼控制器后，在发电机G3励磁控制系统分别安装PSS1A传统控制器和附加鲁棒阻尼控制器，施加扰动2，验证发电机附加鲁棒阻尼控制器和文中机网阻尼协调控制的有效性，仿真结果如图11所示。

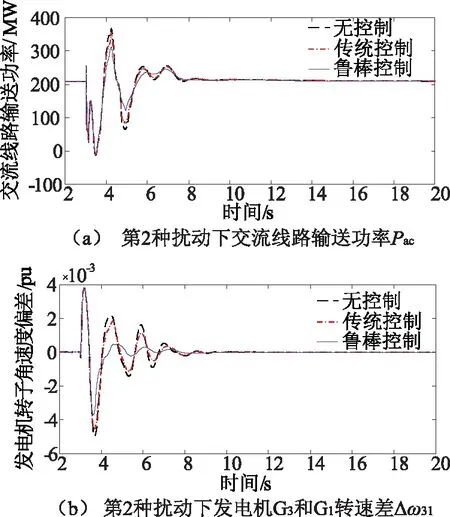
图11 发电机G3传统PSS控制与附加鲁棒控制的控制效果对比

可见，在扰动(2)下，发电机励磁传统控制器对区域间的低频振荡有一定的抑制作用，但控制效果不明显。而本文的发电机励磁附加鲁棒阻尼控制器能够明显地提高后续摆动的阻尼，加快系统恢复稳定运行的速度。在HVDC安装附加鲁棒阻尼控制器后，发电机安装附加鲁棒阻尼控制器能够进一步抑制区域间的低频振荡。相比仅HVDC安装鲁棒控制器，发电机励磁和HVDC都安装鲁棒控制器的系统稳定性更高，对区域间低频振荡抑制效果更好，能进一步提高系统暂态稳定性，从而验证了文中机网阻尼协调控制的正确性、有效性。

4 结束语

(1)运用TLS-ESPRIT算法辨识出系统的振荡模式和低阶开环模型，结合H2/H∞控方法在HVDC和发电机设计了附加鲁棒阻尼控制器，用于抑制区域间的低频振荡。该方法采用线性矩阵不等式的求解方法和输出反馈设计控制器，求解容易，控制器设计简单，便于工程实践；

(2)时域仿真表明，附加鲁棒阻尼控制器对区域间的低频振荡抑制效果良好，具有较强的鲁棒性，在降低首摆幅度、增加后续摆的阻尼和恢复系统稳定运行的速度等方面明显优于传统附加阻尼控制器；

(3)发电机附加鲁棒阻尼控制器能进一步抑制区域间的低频振荡，增加后续摆的阻尼，提高系统稳定性，从而验证了文中机网阻尼协调控制的有效性，可为实际工程的机网阻尼协调提供参考价值。