一种基于自适应滤波器的改进ip-iq无功电流检测方法*

孙曙光，刘建强，杜太行，刘旭林

(河北工业大学 控制科学与工程学院，天津 300130)

0 引 言

随着电力电子的飞速发展，各种电力电子装置以及其他非线性负荷投入电网中，由此产生了大量的无功，对整个电网的安全以及经济运行造成严重的影响。因此，电力部门对用户电能质量提出了越来越高的要求。准确和快速检测无功电流是实现补偿无功的关键环节[1-2]。目前在三相电路中，ip-iq无功电流检测方法，由于其检测方法简单，计算量少，实时性高等优点而得到了广泛的应用[3-4]。但是，低通滤波器(LPF)对这种检测方法有很大的影响，传统低通滤波器在响应速度与检测精度上很难同时兼顾[5-6]，近几年，如何设计一种既能满足检测精度又能提高响应速度的滤波器成为了研究的热点。文献[7-10]提出了把自适应滤波器作为检测方法中的低通滤波器，通滤波器，提高了无功电流检测的精度和响应速度。但是，该种自适应滤波器在采用传统变步长时，在收敛速度、跟随性能与稳态精度方面存在矛盾。对此，学者们提出了许多可以调整迭代步长的自适应滤波器[11-13]，以改善自适应滤波器的性能。

在以上研究的基础之上，文中采用变步长最小均方(LMS)自适应滤波器取代传统的低通滤波器，进行无功电流的检测，对其检测原理进行分析，同时引入洛伦兹(Lorentzian)函数进行步长的调节，在对其步长调节特性进行分析的基础之上，对整体无功电流检测方法进行了MATLAB仿真与DSP实测实验分析，并与其它方法进行对比分析。

1 无功电流检测原理

1.1 ip-iq检测方法原理

ip-iq检测方法基本原理图，如图1所示。

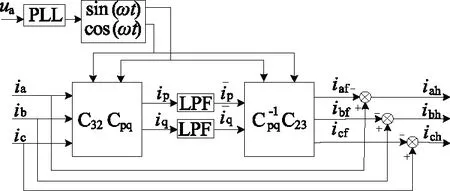
图1 ip-iq检测方法原理图

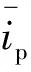
1.2 自适应滤波器原理

针对传统低通滤波器的不足，采用自适应滤波器替代传统的低通滤波器。自适应滤波算法由于其结构简单、计算量小、易于实现等优点而被广泛应用[10-11]，自适应滤波器最常用的是横向FIR结构,如图2所示。

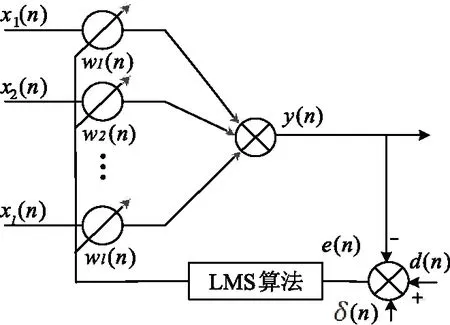
图2 自适应滤波器原理图

其中d(n)表示滤波器在n时刻期望值;y(n)为自适应滤波器在n时刻输出值;e(n)是d(n)和y(n)之差，作为自适应滤波器的反馈信号。X(n)为参考输入信号矢量;W(n)为滤波器输入值的权值。X(n)和W(n)计算如下：

X(n)=(x1(n)，x2(n)，…，xl(n))T

(1)

W(n)=(w1(n)，w2(n)，…，wl(n))T

(2)

滤波器输出与期望输出的误差号：

e(n)=d(n)-y(n)=d(n)-WT(n)X(n)

(3)

其均方差为：

J=E[e2(n)]=E[d2(n)]-

2E[d(n)WT(n)X(n)]+E[WT(n)X(n)XT(n)W(n)]

(4)

应用最速下降算法，搜寻性能曲面的最小点，计算权向量的迭代公式为：

W(n+1)=W(n)+μ(-▽J)

(5)

式中μ为正常数，称为步长因子。

在最速下降算法中，为了进一步获得系统的最佳维纳解，必须要得到输入和期望信号的相关信息，当期望信号未知时，就不能确定它们的相关特性，需要估计梯度向量。LMS自适应算法运用瞬时均方误差对瞬时抽头权向量求梯度：

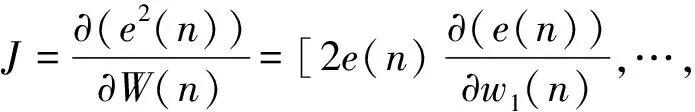
(6)

由式(5)、式(6)可得到向量更新方程：

W(n+1)=W(n)+μ(-▽J)=W(n)+2μe(n)X(n)

(7)

由此可以推出滤波器算法的流程：

y(n)=WT(n)X(n)

e(n)=d(n)-y(n)

W(n+1)=W(n)+2μe(n)X(n)

(8)

式中期望信号d(n)可能会受到噪声信号干扰，当接近最佳权系数值时，会有较大波动，这将导致较大失调[7]。在ip-iq法无功电流检测中，自适应滤波器的应用原理如图3所示[3,7]。

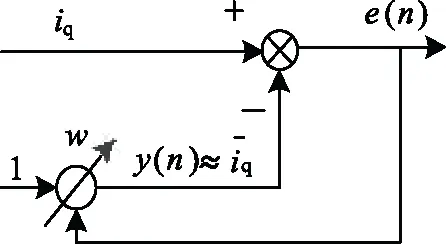
图3 用于无功电流检测的自适应滤波器原理图

在滤波器中，输入信号iq(n)表示pq坐标系下q轴负载电流的采样值，参考输入信号为直流量1，代表参考输入信号的权值，自适应滤波器最终输出为y(n)，e(n)是iq(n)和y(n)之差，作为自适滤波器的误差反馈信号。所以ip-iq法无功电流检测中自适应滤波器算法流程如下：

y(n)=w(n)·1

e(n)=iq(n)-y(n)=iq(n)-w(n)

w(n+1)=w(n)+2μe(n)

(9)

将iq(n)中的直流分量视为期望信号，其他视为干扰信号。权值w(n)由误差反馈信号e(n)进行调节，权值w(n)跟踪最佳权值变化时，输出信号也就跟随直流分量变化，因此可以将iq(n)中的直流分量检测出来。

2 自适应滤波算法步长因子分析

步长因子μ需要同时使响应速度和稳态失调达到平衡。在满足收敛条件的LMS算法中，当离最佳值较远时，要提高算法迭代收敛速度的充要条件是选择较大的迭代步长；当离最佳值较近时，选用较小的迭代步长。基于此，文献[14]提出了基于Sigmoid函数的变步长LMS自适应滤波器(SVSLMS)，将步长因子μ(n)与误差信号e(n)建立Sigmoid函数形式的关系，函数表达式为：

(10)

式中α控制S函数的形状，决定曲线上升的快慢，β控制S函数的取值范围。由于μ(n)随着e(n)的减小而减小，当e(n)为零时，μ(n)也减小为零。

该算法可以解决LMS算法在响应速度和稳态失调之间的矛盾，但是在接近于稳定时，即在e(n)接近于零的时候，步长因子μ(n)变化较慢，LMS算法达到稳态时需要较长的时间，稳定性较差，并且Sigmoid函数结构较为复杂，在实时系统中需要高性能的处理器。因此，文中采用了一种Lorentzian函数的变步长LMS自适应滤波器[15]，函数表达式为：

(11)

式中 参数α用于控制收敛速度，其值越大，收敛速度越快；参数δ用于控制稳态阶段函数的形状，即误差信号接近零时步长因子的变化程度。变步长因子融合了前后两次误差e(n)和e(n+1)，降低了外部噪声对步长因子的影响，具有更强的抗干扰性能。

根据公式中各个参数对函数性能的影响，文中设定Sigmoid函数参数α=0.06，β=0.037，Lorentzian函数中参数α=0.006，δ=0.01。图4分别是Sigmoid函数与Lorentzian函数的μ(n)响应曲线。

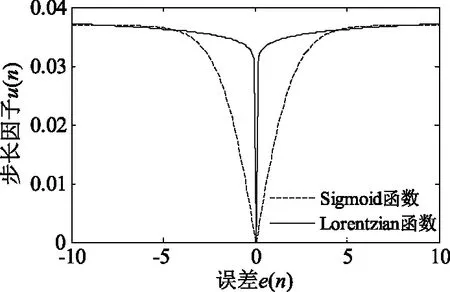
图4 Sigmoid函数与Lorentzian函数的步长响应

由图4可以看出，在收敛的初始阶段，Lorentzian和Sigmoid函数的步长因子μ(n)都可以到达最大值，随着收敛过程的进行，e(n)不断减小，当收敛进入稳态阶段时，Sigmoid函数的步长因子μ(n)收敛速度较慢，而Lorentzian函数的步长因子μ(n)能够快速收敛，因此Lorentzian函数对应的步长参数响应速度比Sigmoid函数对应的步长参数响应速度快。

基于上述分析，文中采用Lorentzian函数的变步长LMS自适应滤波器。同时为了保证算法的稳定性，对步长因子μ(n)进行限幅：

(12)

为了保证算法的快速性，μmax应选择不大于1的正数，μmin的选择选择满足收敛速度和稳态失调的要求，应选取一个较小的正数。文中取μmin=0.001，μmax=0.1。

3 仿真及实测实验结果与分析

3.1 仿真结果与分析

仿真实验中电网电压为220 V/50 Hz，接入由带阻感负载的三相不控整流桥，其中直流侧负载L=1 mH、R=2.5 ，图5为三相负载电流。

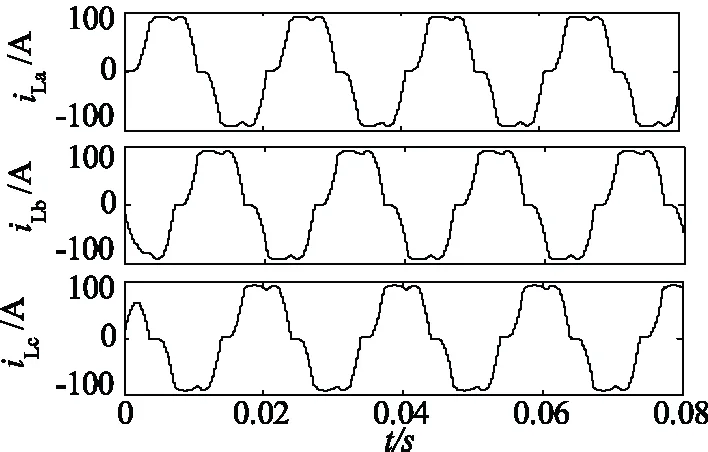
图5 三相负载电流

针对传统ip-iq法无功电流检测，文中设计了二阶Butter worth低通滤波器，但低通滤波器的截止频率带来如下的问题，截止频率小可保证稳态时失调小，但是响应速度慢；截止频率大可使响应速度快，但是稳态时失调变大。因此，需要对传统ip-iq法进行仿真分析，得到最佳截止频率。图6为选择不同的截止频率而得到的iq中的直流分量。

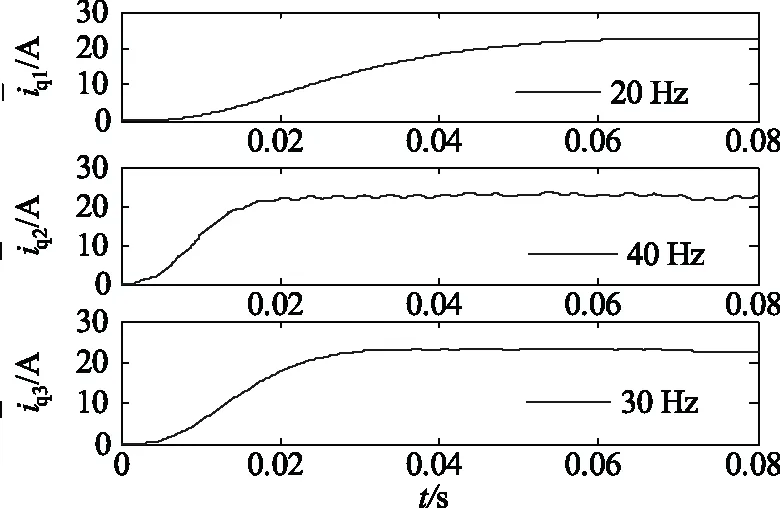
图6 不同截止频率下iq的直流分量

由图6可以看出截止频率为20 Hz时，稳态失调最小，但是响应速度最慢，截止频率设置为40 Hz时，响应速度最快，但是稳态失调程度最大，截止频率为30 Hz时可兼顾响应速度和稳态失调。因此，文中截止频率设置为30 Hz。

选定低通滤波器最优参数后，分别对传统ip-iq无功电流检测方法、基于Sigmoid函数变步长自适应滤波器的无功电流检测方法、和基于Lorentzian函数变步长自适应滤波器的无功电流检测方法的检测结果进行比较。根据上文对步长因子对函数动态响应性能的影响，设置Sigmoid函数中设置α=0.06，β=0.037，Lorentzian函数中设置α=0.006，δ=0.01。

利用FFT分析A相负载电流并通过计算得到A相理论的基波无功电流iaqf。

图7分别是传统ip-iq检测方法、Sigmoid函数检测方法以及Lorentzian函数检测方法得到的三相中A相的基波无功电流iaqf1、iaqf2和iaqf3，表1分别是三种检测结果的幅值，并与理论值比较。

由图7可以看出iaqf1约在0.02 s ～0.03 s趋于稳定，iaqf2约在0.02 s趋于稳定，iaqf3约在0.01 s趋于稳定。由表1可以看出文中采用的方法得到的基波无功电流的精度最高。

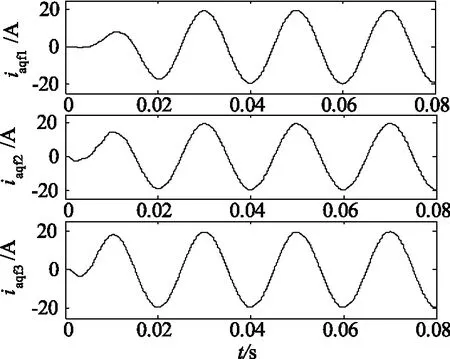
图7 A相基波无功电流

基波无功电流iaqfiaqf1iaqf2iaqf3幅值/A19.5018.4319.4519.47

3.2 实测实验结果与分析

在实际测试实验中，电网电压为220 V/50 Hz，接入非线性负载，由带阻感负载的三相不控整流桥产生，其中直流侧负载L1=10 mH、R1=20 Ω。采用TMS320F28335 DSP 芯片作为核心控制器，设计了无功电流检测的实验系统，系统结构如图8所示。

图8 基于DSP无功电流检测系统

将检测的电网电压和负载电流的信号，经过信号调理电路，对信号进行放大和滤波，通过DSP中A/D完成信号采集；采用LM393芯片，实现电网A相电压的过零检测，经过CD4046实现相位同步，通过DSP的ECAP功能捕捉锁相电路的输出信号，完成锁相功能。在DSP中经过算法程序得到检测结果，并通过触摸屏进行显示，为了对实验结果分析，同时将检测结果经过D/A输出，用示波器对其采集并且分析，文中对实验结果分析均采用该种方法。

在实验中，分别对三种方法进行测试，通过触摸屏设置的按钮切换检测方法中的三种滤波器，检测过程如图9所示。

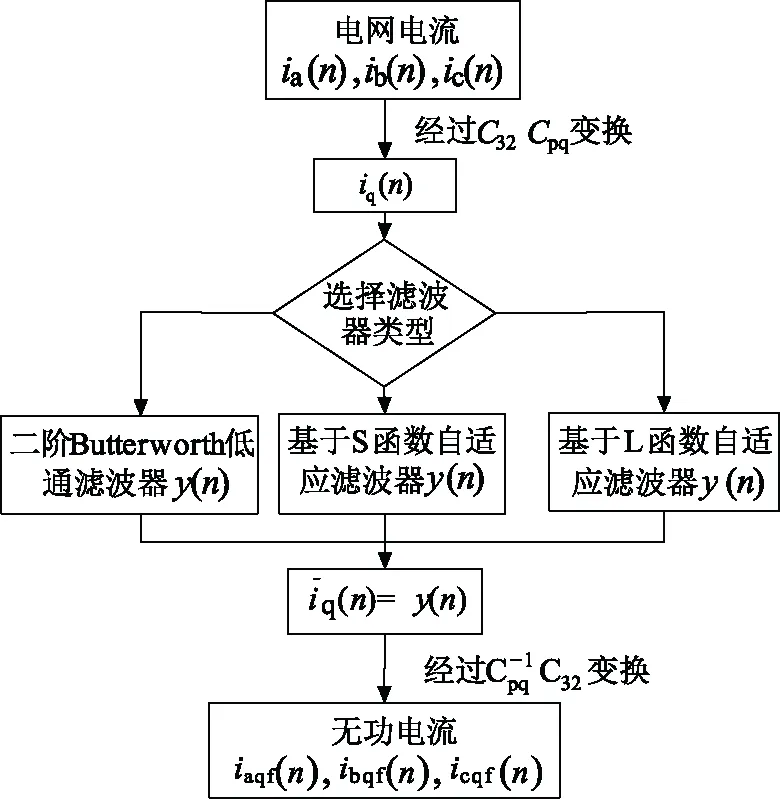
图9 检测方法实现过程

利用锁相环，在A相电压过零点时，开始检测负载电流，并且计算无功电流。图10为A相负载电流。

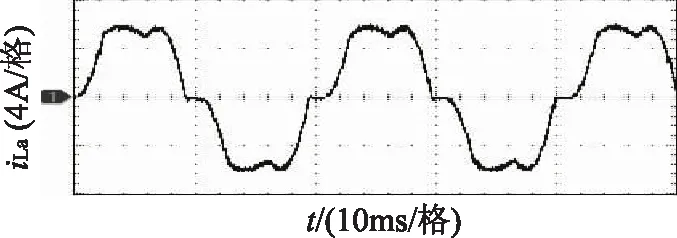
图10 实测实验A相负载电流

在实测试验中，为了测试每种检测方法的运行效率与速度，计算了每种方法进行一次采样计算无功电流瞬时值所需要的时间，通过对程序运行所需时钟周期的计算得到程序运行所需时间，传统ip-iq检测方法所用时间为3.73×10-5s, Sigmoid函数检测方法所用时间3.93×10-5s，Lorentzian函数检测方法所用时间2.67×10-5s，很明显文中采用的方法所需时间最少。

在DSP中，首先利用FFT方法分析A相负载电流，并且通过计算得到A相理论上的基波无功电流iaqf。

图11分别是传统ip-iq检测方法、Sigmoid函数检测方法以及Lorentzian函数检测方法得到的三相中A相的基波无功电流iaqf1、iaqf2和iaqf3，表2是基波无功电流检测结果的幅值。

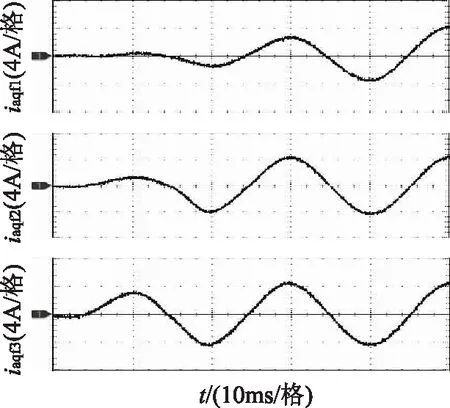
图11 实测实验A相基波无功电流

基波无功电流iaqfiaqf1iaqf2iaqf3幅值/A4.434.264.284.39

4 结束语

首先对传统ip-iq无功电流检测方法中的低通滤波器进行改进，将基于Lorentzian函数的变步长自适应滤波器作为检测方法中的低通滤波器。经过MATLAB与实测实验分析表明，与传统ip-iq检测方法相比，采用变步长自适应滤波器的方法在保证检测精度的前提下明显提高了响应速度；同时将采用的方法与基于Sigmoid函数变步长自适应滤波器的检测方法相比，具有更快的响应速度；再者文中采用的无功电流检测方法运算速度更快，可保证检测的实时性，具有实际应用价值。在此基础之上，针对所选方法中关键参数的选取对不同检测对象适用性问题的研究是今后需要努力的方向。