基于注入信号与小波能量的小电流接地故障选线研究

王建元，张峥

(东北电力大学 电气工程学院，吉林 吉林 132012)

0 引 言

在我国3 kV～66 kV中低压配电网中，其中性点一般选取不接地或者经消弧线圈接地的小电流接地方式。当出现最常见的单相接地故障(约占所有故障80%)，网络线电压依然对称，故障零序电流甚小，故可带故障运行1 h ～2 h。但为了避免故障进一步扩大，造成更为严重的两相或者多点接地短路，必须尽快选出故障线路，排除故障。文献[1]指出系统故障信号微弱，实际线路结构复杂，故障情况多变，目前选线效果并不理想，因此如何精准快速的识别故障线路便成为我们研究的重点。

近年来，研究学者热衷于利用小波变换良好的时频特性对暂态分量进行精细分析，可以克服稳态算法灵敏度低，受消弧线圈影响等问题，文献[2-3]体现了小波工具在处理不规则、不稳定、突变的暂态信号时拥有着出色的能力，但故障的暂态分量存在周期较短，提取困难等问题。文献[4-6]提出故障发生后利用母线电压互感器(PT)向网络中导入特殊频率(220 Hz)的信号，将能够被信号探测器捕捉到的线路选为故障线路，但由于PT容量受限，入住信号能量较小，当存在较大过渡电阻时，健全馈线也会有分流的注入信号，导致探测器捕捉到多条线路无法进一步选线。文献[7-8]提出一种基于HHT小电流接地故障选线与在线故障定位的方法，但实际应用并不理想。

鉴于上述原因，提出利用小波工具对各条馈线中的注入信号进行低频能量计算，通过比较能量的大小进行选线。在大量的仿真实验过程中，考虑了可能影响选线结果的因素，例如故障点距离母线的长度，线路参数的大小，中性点的接地方式以及故障合闸角的大小等。充分利用提取的稳态注入信号，克服了暂态分量存在时间短、难以提取的问题，并成功的解决了注入法在存在过渡电阻时信号分流无法选线的问题。

1 注入信号法

1.1 注入信号法原理

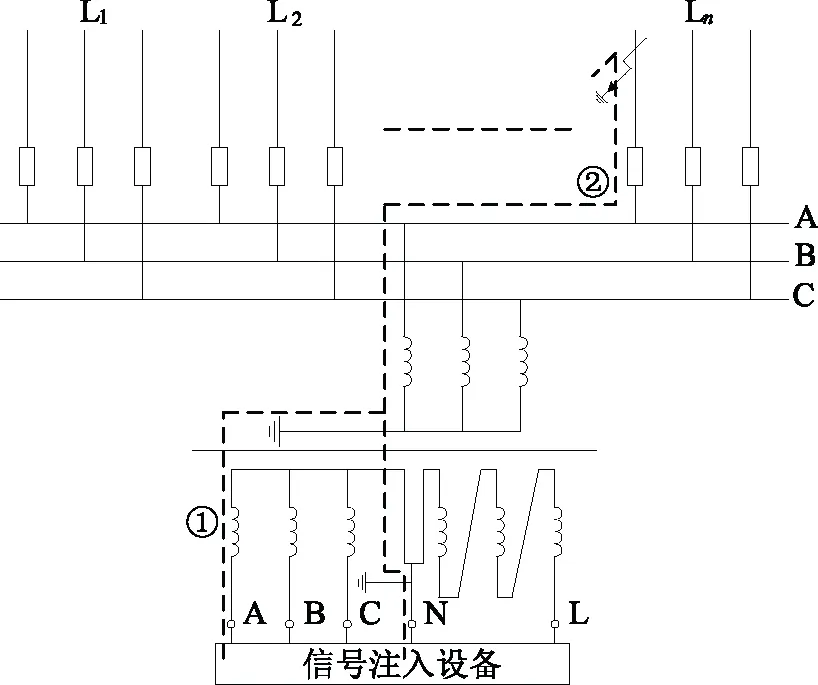
图1 信号注入原理图

当信号注入设备探测到以上电压大小的改变后，锁定出故障相A，然后迅速在A与N的线端中间自动接入信号发生源，因此，注入的特殊频率信号通过绕组互感经过图1中虚线①、②的路径流入大地，最后利用线路中的探测装置即可选线。

1.2 注入信号频率

为了不对配电网的正常运行造成过多影响，我们所注入信号的能量越小越好，但是配电网络是一种高电压、大电流的非线性强电系统，其中存在着大量的工频及各次谐波信号，即便某些谐波含量较低，但它的能量也会远远大于注入信号的能量。因此，为了避免被网络中已经存在的信号所掩盖，我们必须使注入信号具有特殊性、单一性，易于探测器的检测。经过综合考量，为了保证选线结果不被工频基波及其各次谐波所影响，选择频率在工频N次和N+1次谐波之间的特殊电流信号作为注入信号。本文选取f=220 Hz的电流信号作为注入信号，由于利用小波工具分解信号所得到都低频系数a对应的频率范围在0 Hz ～312.5 Hz，所以在计算小波能量时只需计算各条线路的低频能量即可。

2 小波能量法

2.1 小波变换简介

小波变换(WT)是一种继Fourier之后能够通过缩放与平移来细分信号的多分辨率分析手段，对于处理复杂多变的局部信号方面，其拥有着优越的时频特性。利用传统暂态小波变换法去解决配电网选线问题是因为在接地故障发生瞬间，系统馈线中的暂态零序电流具有非线性、不稳定的特点，这种信号非常合适小波工具提取及细化分析。

小波变换是以多尺度分析(MRA)理论作为基础结构，满足如下的双尺度差分方程：

(1)

(2)

式中φ(t)为尺度函数；ψ(t)为小波函数；h(n)和g(n)为小波分解滤波器组系数。

为了能在各种范围内由粗至细，由轮廓到细节上洞察波形的特征，离散型小波函数通过塔式多尺度分析与快速重构的马拉特(Mallat)算法把原始函数进行变换，在此过程正如反复利用一组低通与高通的滤波器，得到输入信号的低频与高频分量，各占信号频带的一半。采样频率在每次分解中缩短至原来的1/2，低频分量被反复分解，得到一层又一层的低频与高频分量。

2.2 小波能量

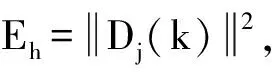
3 仿真验证

配电网发生单相电阻性接地故障的示意图如图2所示，此仿真模型为一所具有3条代表性馈线的110 kV/10 kV变电站，各条馈线正序、负序参数[9]如下：

架空线：R1=0.414 1 Ω/km，R0=0.564 1 Ω/km,

L1=1.079 mH/km，L0=7.392 4 mH/km,C1=10.74

nF/km，C0=4.209 nF/km;

电缆：R1=0.305 0 Ω/km，R0=0.453 23 Ω/km,

L1=0.305 3 mH/km，L0=6.672 7 mH/km,C1=196.2

nF/km，C0=196.2 nF/km。

其中将线路L1设置为15 km电缆线路;L2为20 km架空线路;L3为4 km电缆与6 km架空线的混合线路，变压器采用Y/Yn接线[10]。馈线末端负荷的大小并不能影响选线结果，故全部选用ZL=300+j100 。

考虑中性点接地方式以及消弧线圈的补偿作用对该方法选线结果的影响，将开关K跨接在变压器低压侧中性点与消弧线圈之间，当开关K断开时，表示中性点不接地系统，当开关K闭合时，表示谐振接地系统。消弧线圈电感LN的大小为：

(3)

式中fN为50 Hz工频；l为系统线路的总长；C0为馈线的零序电容；v为失谐度，它的大小代表了不同的补偿度，v=(IC-IL)IC。通过Simulink构建系统仿真模型，为了验证该方法具有较广泛的适用范围，仿真过程中组合各种不同的故障情况，故障时刻统一设置为0.05 s，选线结果如表1所示。

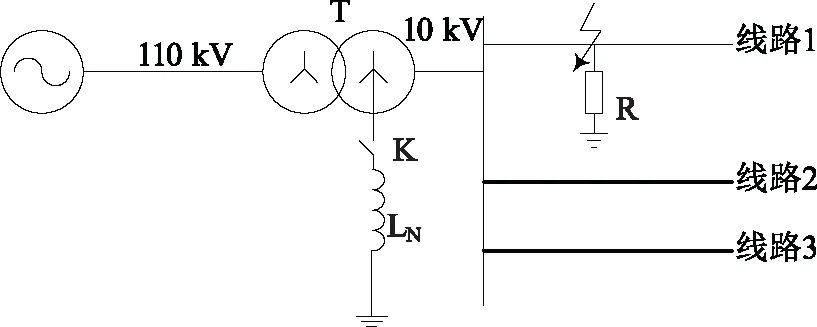
图2 配电网单相接地故障示意图

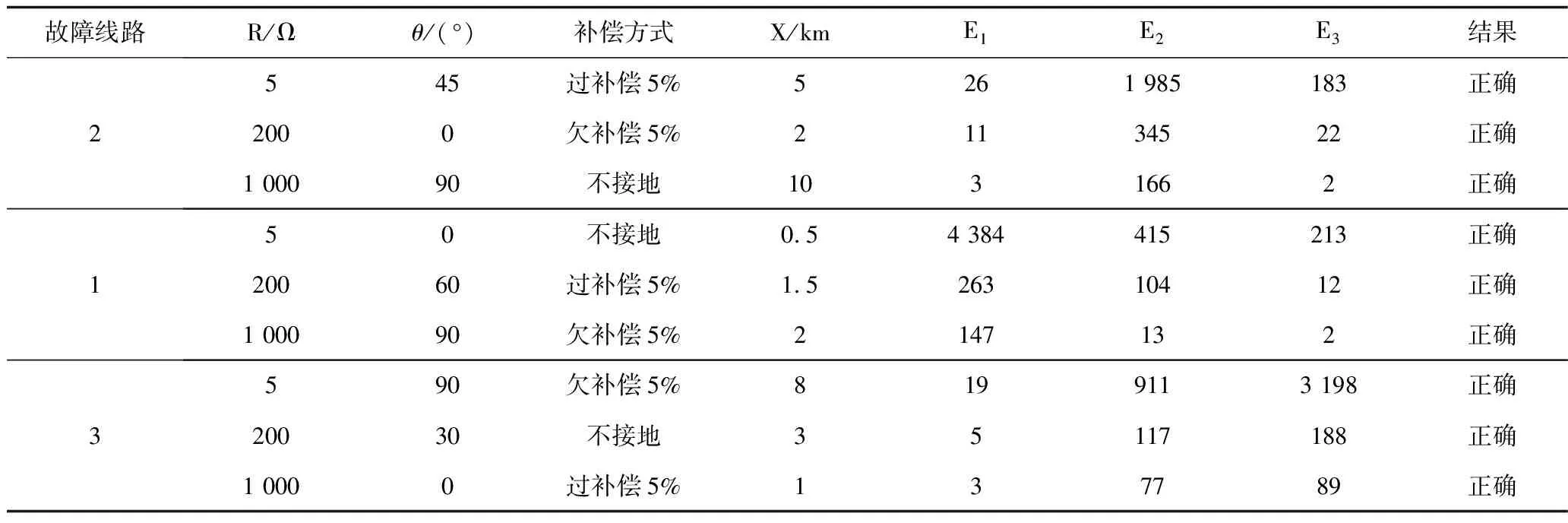
故障线路R/Ωθ/(°)补偿方式X/kmE1E2E3结果2545过补偿5%5261 985183正确2000欠补偿5%21134522正确1 00090不接地1031662正确150不接地0.54 384415213正确20060过补偿5%1.526310412正确1 00090欠补偿5%2147132正确3590欠补偿5%8199113 198正确20030不接地35117188正确1 0000过补偿5%137789正确

在系统模型发生故障的同时，向网络中注入f=220 Hz能量较弱的低频电流信号，通过设置在各条馈线上滤波器的提取，利用db5小波工具对其进行变换得到对应的低频系数a1～a5，并计算出低频能量，比较三条线路稳态低频能量E的大小，能量较大的选作为故障线路。由表2可知，选线结果均正确，成功解决了当存在过渡电阻时传统注入法存在信号分流无法选线的问题，同时也克服了暂态方法存在的难题，该方法不受故障合闸角、补偿类型、故障距离的影响，并具有一定的抗过渡电阻能力，可靠性高，能够准确选择出故障线路，但随着过渡电阻的增加，各条线路所计算出的低频能量也在随之减小，且它们之间的能量大小也越来越接近。

4 算法适应性分析

4.1 抗干扰能力

在实际的配电网故障情况中，往往存在一定的噪声干扰，在此情况下，该方法仍然可以选择出故障线路。向注入信号中叠加平坦的白噪声，其讯噪比设为25 dB，在不同合闸角及补偿度的情况下馈线2距离母线1 km处发生单相接地故障，接地电阻200 Ω，选线结果见表2。

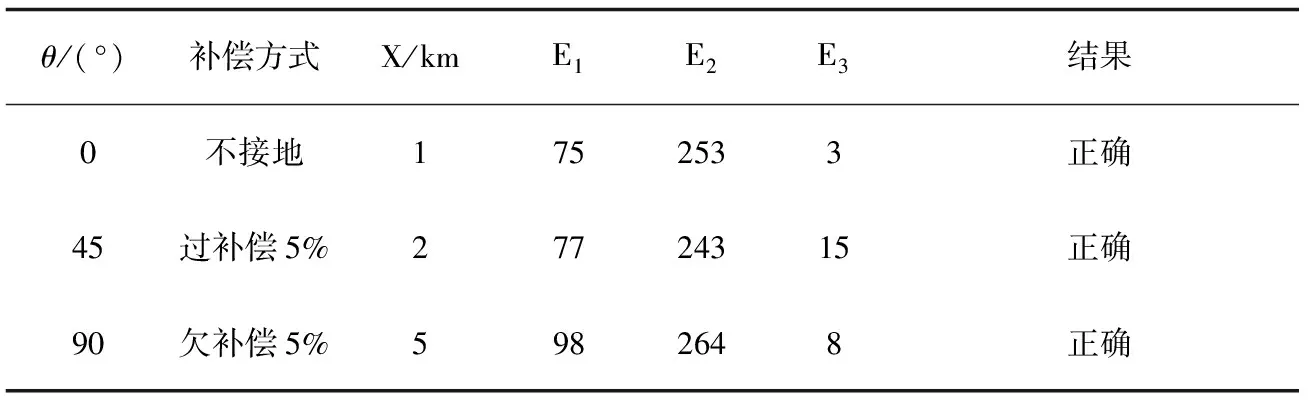
表2 噪声干扰下的选线结果

4.2 抗过渡电阻能力

以架空线路为例，当馈线2发生低阻性接地，其过渡电阻50 Ω，合闸角0 Ω，过补偿5%，接地点距离母线5 km，故障时刻设在0.05 s，仿真过程中各线路注入电流波形如图3所示。

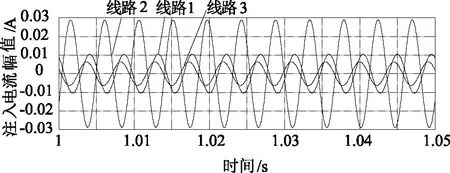
图3 馈线2低阻50 Ω接地时各馈线注入电流波形

对图3中提取的各条馈线1 s ～2 s稳态注入电流进行小波变换，将低频系数通过公式计算得到各线路小波能量E，结果如图4所示。当发生接地电阻为50 Ω的单相故障时，选线成功。

当馈线2发生高阻性接地，过渡电阻1 500 Ω，合闸角30 Ω，中性点不接地，接地点距离母线3 km，故障时刻设在0.05 s，仿真过程中各线路注入电流波形如图5所示。

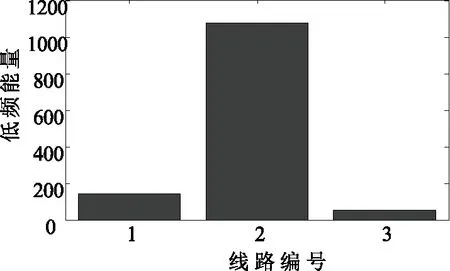
图4 各馈线稳态低频小波能量

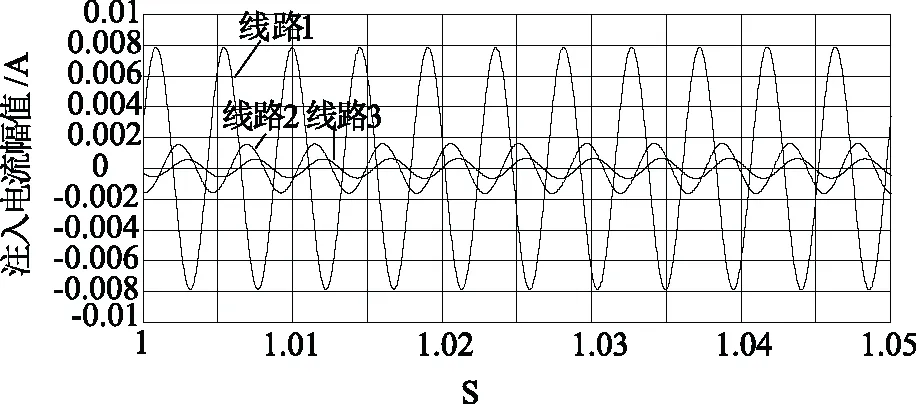
图5 馈线2高阻1 500 Ω接地时各馈线注入电流波形

由于过渡电阻过高，造成健全馈线1中的注入信号能量高于故障线路2，选线失败，如图6所示。由此可知，该方法针对于架空线路虽然具有一定的抗过渡电阻能力，但当接地电阻过高时失效。

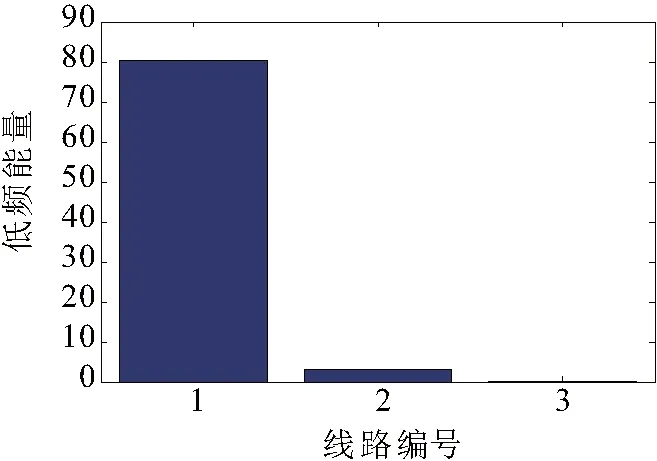
图6 各馈线稳态低频小波能量

为了解决这一问题，我们可以选择通过比较各条馈线所提取注入电流的相位的方法进行选线，如图7所示。

图7 各馈线注入信号相位对比

5 结束语

在分析注入法与小波能量法选线原理基础上，提出了将两者结合的选线新方法。通过对各条馈线中220 Hz稳态注入信号的低频能量计算、分析及比较成功解决了高阻性接地系统注入信号分流的无法正常选线问题，并克服了已往小波能量对于暂态能量计算时，暂态信号存在时间短，难以提取等问题。通过搭建系统模型，针对各种不同故障情况进行了大量的仿真实验，验证该方法不受合闸角、故障点距母线距离、补偿方式等因素的影响，并对其进行了抗干扰及抗过渡电阻能力的适应性分析，可以准确选线。