广义Gauss-Seidel迭代法的预测-校正方法

伊马木·麦麦提 阿布都热西提·阿布都外力 娜扎开提·阿迪力

(新疆大学数学与系统科学学院，新疆 乌鲁木齐 830046)

1 引 言

考虑线性方程组

Ax=b,

(1.1)

其中A是n×n的非奇异矩阵，b是n维向量.

将系数矩阵A进行分裂为A=D-L-U，其中D是对角矩阵，L是下三角矩阵，U是上三角矩阵.则经典的Gauss-Seidel迭代法为

x(k+1)=(D-L)-1Ux(k)+(D-L)-1b，

k=1,2,3,…,

(1.2)

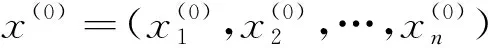
对部分线性方程组而言，用经典Gauss-Seidel迭代求解，敛速度不理想，为了解决该问题，本文推出了广义Gauss-Seidel(简称为广义G-S)迭代法和它的预测-校正方法.

2 广义G-S迭代法

将系数矩阵A进行分裂为A=Dm-Lm-Um，其中Dm是带状对角矩阵，带宽为2m+1,Dm的各元素是

(2.1)

其中m=0,1,2,…,(n-1)/2，Lm与Um是矩阵A-Dm的严格上下部分，Dm,Lm,Um分别为

Dm=

如果取矩阵Dm-Lm作为迭代矩阵(Dm-Lm)-1Um，则得到文献[1]中的广义G-S迭代方法.迭代公式是

x(k+1)=(Dm-Lm)-1Umx(k)+(Dm-Lm)-1b，

k=0,1,2,….

(2.2)

若分裂矩阵中取矩阵Dm-Um作为迭代矩阵(Dm-Um)-1Lm，则推出的迭代方法是

x(k+1)=(Dm-Um)-1Lmx(k)+(Dm-Um)-1b，

k=0,1,2,….

(2.3)

当m=0时式(2.2)与(2.3)表示的是正，反方向的经典G-S迭代法，计算公式分别为

(2.4)

(2.5)

3 广义Gauss-Seidel迭代法的预测-校正方法

为了改进广义G-S迭代法的收敛速度,将两种广义G-S迭代方法相匹配，生成广义G-S迭代法的预测-校正方法：

(3.1)

本方法先用(2.2)的广义G-S迭代法预测y(k+1)的值， 然后用(2.3)的广义G-S迭代法校正x(k+1). 当m=0时，预测公式和校正公式的分量形式分别为

(3.2)

4 收敛性分析

迭代法的收敛性依赖于迭代矩阵，设迭代矩阵为G,则迭代法收敛的充分必要条件是ρ(G)<1(其中ρ是迭代矩阵的谱半径)，充分条件是‖G‖<1(其中‖‖表示为任意范数).下面给出了一些比较容易验证的充分条件.

引理1[3]若M=(Mij)和N=(Nij)都是n×n的矩阵，并且M是严格对角占优矩阵，则矩阵M-1N的特征值满足

(4.1)

定理1如果A为严格对角占优矩阵，则新广G-S迭代法是收敛.

证明将严格对角矩阵A分裂为A=M+N，其中M=Dm+Um,N=Lm并且M是严格对角占优矩阵.从上述的引理可得

其中

(4.2)

我们先证:ρ=maxρi<1, 因为A是严格对角占优矩阵，所以满足

(4.3)

由式(4.3)可以推到

(4.4)

由不等式(4.4)可得ρ(M-1N)<ρ<1.据代法收敛的充分必要条件，新广义G-S迭代法是收敛.

定理2[2]如果A为不可约弱对角占优矩阵,则新的广义G-S迭代法是收敛.

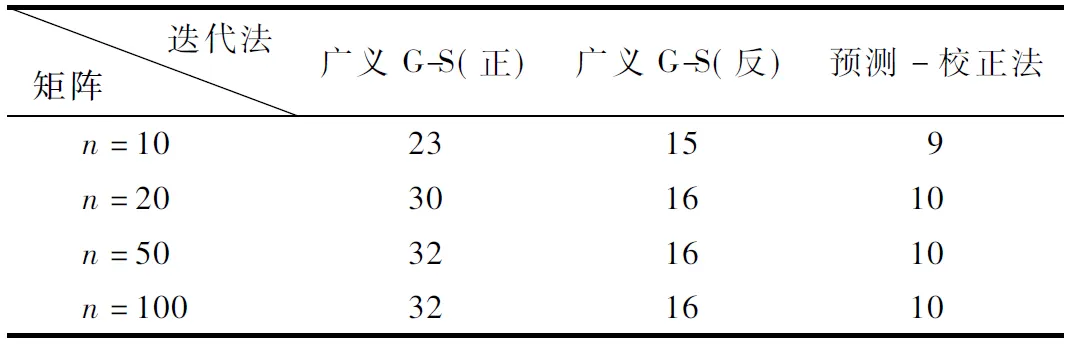
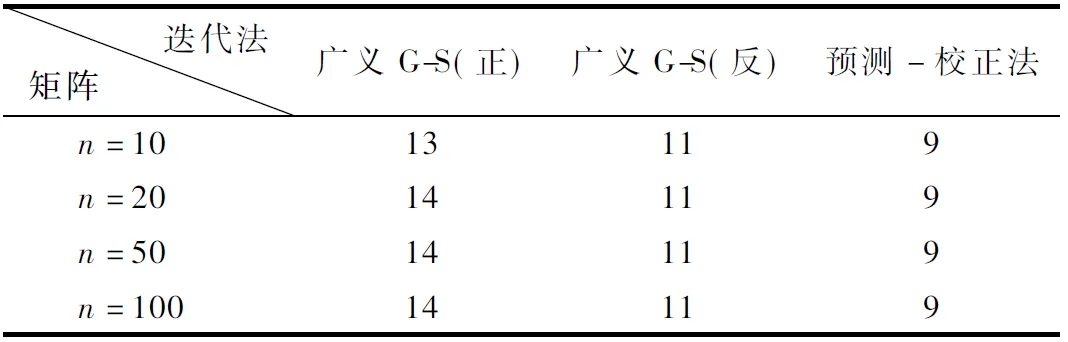
定义设A=(aij),B=(bij)是n×n的矩阵，如果aij与bij满足aij≤bij(aij≤bij)，则矩阵A与B 的关系表示为A≤B(A

定理3[4]设矩阵A=(aij)，B=(bij)若A≤B，bij≤0，且A是M-矩阵，则B也是M-矩阵.

定理4[4,5]若A∈Zn×n，则以下命题相互等价(其中0是零矩阵)：

(1)A为非奇异M-矩阵；

(2)A是非奇异，且A-1≥0;

(3)存在A的一种分裂A=P-Q(正则分裂),使得P-1≥0，Q≥0,且ρ(P-1Q)<1;

定理5如果A是M-矩阵，则新广义G-S迭代法是收敛.

证明设矩阵A分裂为A=P-Q,其中P=Dm-Um，Q=Lm.

因为A是M矩阵，显然，P≥A，Q>0，由定理3可知分裂矩阵P也是M-矩阵.

又因为P是M-矩阵，根据定理4的命题(2)，(3)可知P是非奇异，P-1≥0，且ρ(P-1Q)<1，所以迭代矩阵的谱半径满足条件：ρ(P-1Q)<1，若系数矩阵A为M-矩阵，则新广义G-S迭代法是收敛.

定理6广义G-S预测-校正法收敛的充要条件是ρ(G正·G反)<1,收敛的充分条件是‖G正·G反‖<1.

证明用预测-校正公式(3.1)很容易推到:

x(k+1)= (Dm-Um)-1Lm(Dm-Lm)-1Umx(k)+

(Dm-Um)-1Lm(Dm-Lm)-1b+

(Dm-Lm)-1b.

(4.5)

由迭代式(4.5)可知预测-校正方法的迭代矩阵为G=(Dm-Um)-1Lm(Dm-Lm)-1Um，

根据矩阵的运算性质，可得迭代矩阵G刚好为两种迭代矩阵的乘积，即G=G正·G反，因此预测-校正方法收敛的充要条件是：ρ(G正·G反)<1,收敛的充分条件是：‖G正·G反‖<1.

由上面所述的一些定理可知，如果系数矩阵是对角占优矩阵，不可约弱对角占优矩阵，M-矩阵等情况下解线性方程程组的广义G-S预测-校正法是收敛的.

5 数值实验

为了比较迭代法的收敛速度，下面给了数值例子，根据其结果，说明这些方法的优缺点.

例1[5]设线性方程组(1.1)中A，b值分别为

此线性方程组的精确解是x*=(1,1,…,1)T,迭代初始向量是x(0)=(0,0,…,0)T.

表1 当m=0时各种迭代法的迭代次数(经典G-S法)

表2 当m=1时各种迭代法的迭代次数

由表(1),(2)可知，广义G-S迭代法及预测-校正方法解线性方程组(1.1)均收敛，而反方法的收敛速度比正方法较快，预测-校正算法的收敛速度比两个方法都快(即取n相同值时，达到同样精度所需迭代次数较少).当参数m取不同值时，三种迭代方法的迭代效果也不相同，m的值越大三种迭代格式的收敛速度越快，迭代次数越少.

6 结 语

以上介绍了基于Gauss-Seidel迭代法的三种广义迭代方法.并在理论和数值计算方面证明了本文中的迭代法是有效的.若三种迭代法均收敛，则正反广义Gauss-Seidel迭代的收敛速度基本相同，预测-校正方法的收敛速度要比这两种广义迭代法更快一些.本文中迭代法的收敛速度依赖于带宽因子m,因此m取的值越大收敛速度也是越快.