共振条件下具有奇异性和无界扰动Duffing方程的周期解(下)
马田田 张铁荟 黄 艳
(1.首都师范大学,北京 100048; 2.济宁学院初等教育学院, 山东 曲阜 273165; 3.枣庄职业学院基础教学部,山东 枣庄 277800)
3 相关引理的证明
3.1 引理2.4的证明
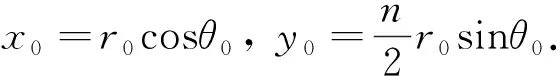
则
因此, 对任意t,s∈[0,2π],

进而可得
η(0)-υ≤u(t)≤u(0)+υ,t∈[0,2π].
由此可知
t∈[0,2π].
由于当x>0充分大时,F(x)是严格递增的, 故对充分大的正数c, 存在a=a(c),b=b(c)(0 从而有 (8) 及 由此可知存在ξ∈(a,b)使得 由条件(h4) 和 (h5) 可知存在正常数ζ使得当c>0充分大时, |b-a|≤ζ. (9) 进而有 |c-a|≤ζ,|b-c|≤ζ. (10) 由(8)可知 2F(a)≤y2(t)+2F(x(t))≤2F(b),t∈[0,2π]. (11) 根据(11)可得F(x(t))≤F(b),t∈[0,2π]. 由于当x>0充分大时,F(x)是递增的, 故当cosθ(t)≥0且c充分大时, 0≤x(t)=r(t)cosθ(t)≤b,t∈[0,2π]. 由 (11)式进一步可知 n2a2+8G(a) ≤4y2(t)+n2x2(t)+8G(x(t)) ≤n2b2+8G(b),t∈[0,2π]. 因此, n2a2+8G(a) ≤n2r2(t)+8G(r(t)cosθ(t)) ≤n2b2+8G(b),t∈[0,2π]. 进而有 t∈[0,2π]. (12) 由条件(h4) 和(h5) 可知对任意ε>0, 存在正常数c1,c2使得当x∈[0,+∞)时, -c1≤G(x)≤εx2+c2. 从而当t∈[0,2π] 且cosθ(t)≥0时, -c1≤G(r(t)cosθ(t))≤εr2(t)+c2. (13) 由(12)和 (13)可得 (14) 根据(9), (14) 和(h5)可知存在0<μ1<1, 0<μ2<1使得当cosθ(t)≥0且c>0充分大时, (1-μ1)a2≤r2(t)≤(1+μ2)b2,t∈[0,2π]. 成立. 证明由[15]中的结果可知当c→+∞时,估计式 t2-t1=o(1) 对任意(x0,y0)∈Γc一致成立. 下面, 我们将给出t2-t1的更精确估计. 为此,仍用引理2.4中的记号.令 不失一般性,假定 f(x)<0,x∈(-1,0). 因此,对任意充分大的c>0, 存在唯一的d(c)∈(-1,0)使得 F(d(c))=F(c). 从而,存在-1 F(d(a))=F(a),F(d(b))=F(b), 这里a和b是引理2.4中给出的常数. 从 (11)可以得到 2F(d(a))≤y2(t)+2F(x(t))≤2F(d(b)), t∈[0,2π]. 故有 2(F(d(a))-F(x(t))) ≤y2(t)≤2(F(d(b))-F(x(t))). (15) 设ta,t*∈[t1,t2] 满足ta 从而 (16) 记 接下来,我们分别估计I1和I2. 因为g(x) 是局部李普西茨连续的, 所以g(x) 在(-1,0)上几乎处处可导并且g′(x) 在(-1,0) 的任一个闭子区间上勒贝格可积.由I1的表达式可知 由[3]的结果可知 这里 因此, 从而有 又由于a (17) 根据I2的表达式可知 从而 这样,我们得到 (18) 根据条件(h5)可得 (19) 从而,根据(18)和(19)可得 进而,当c→+∞时, (20) 根据(17)可知当c→+∞时, 结合(20)可得 (21) 由 (16), (17)和 (21)可知当c→+∞, 估计式 (22) 对于任意 (x0,y0)∈Γc和λ∈[0,1]一致成立.接下来估计t*-ta. 因为x′(t*)=y(t*)=0, 所以对于t∈(ta,t*), 由此可得 ≥ 2(F(x(t*))-F(x(t)))+ 2‖p‖∞(x(t*)-x(t)), 这里 ‖p‖∞=max{|p(t)|:t∈[0,2π]}. 因此,对于t∈(ta,t*), -x′(t)≥ 进而, ≥1. 积分可得 ≥t*-ta, (23) 结合(23)得到 (24) 由(22)和 (24)可知当c→+∞时, 估计式 关于任意 (x0,y0)∈Γc和λ∈[0,1]一致成立. 类似可得 因此,估计式 关于任意 (x0,y0)∈Γc和λ∈[0,1]一致成立. 证明定义W:(-1,+∞)×R→R, 设t*∈(t1,t2) 满足x(t*)=max{x(t)|t1≤t≤t2}. 则 y(t*)=0;y(t)≥0,t∈(t1,t*); y(t)≤0,t∈(t*,t2). 因此,对于t∈(t1,t*), 有 W′(t)=(λp(t)+‖p‖∞)y(t)≥0. 从而W(t)在区间(t1,t*)上是递增的.于是, 当t∈(t1,t*)时, w(t)≤w(t*), 由此可知 y2(t)≤2(F(x(t*))-F(x(t)))+ 2‖p‖∞(x(t*)-x(t)). 这样,当t∈(t1,t*)时, x′(t)≤ 进而, ≤1. 在区间(t1,t*)上积分上述不等式可得 ≤t*-t1, 这里x*=x(t*). 由条件(h5)可推知当x*→+∞时, (25) 记 则当t∈(t1,t*)时, 由此可知当t∈(t1,t*)时, y2(t)≥2(F(x(t*))-F(x(t)))- 2‖p‖∞(x(t*)-x(t)). 进而, x′(t)≥ 因此, 在区间(t1,t*)上积分上述不等式可得 ≥t*-t1. (26) 因为当x*→+∞时, (27) 所以, 类似可得 因此,当x*→+∞时, 根据引理2.4可知 (28) 从而当c→+∞时, 由条件(h4) 可知对于任何充分大的常数A>0, 存在a>0使得 g(x)≥A,x≥a. 记 =J1+J2, 这里 下面分别估计J1和J2. 首先,易知当x*→+∞时, (29) 对于x∈(a,x*), 有 2(F(x*)-F(x))-2‖p‖∞(x*-x) 因此, 通过直接计算可以得到 和 (30) 根据 (26), (29) 和 (30),我们得到 类似地可得 因此,当x*→+∞时, (31) 由于B=2(A-‖p‖∞) 而A是一个可任意大的常数,故由(28)和 (31)可知对任意充分大的α>0, 存在c0>0 使得对任意c≥c0, 有 证明我们将应用引理2.1 来证明定理1.1. 为此,只需证明存在一个正常数ζ 使得若x(t)是方程(5)的一个2π周期解, 则有 x(t)≤ξ,t∈[0,2π]. (32) 令α(>5) 是一个固定常数. 由引理2.6可知当k充分大时, (33) (34) 根据(33)和 (34), 对于充分大的k, 由此可知j>n. 另一方面, 由引理2.5和引理2.6可得 故有j

3.2 引理2.5的证明


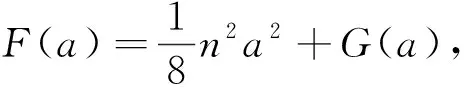



3.3 引理2.6的证明

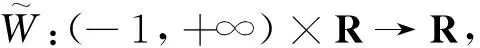






4 定理1.1的证明



