有限大蜂窝格子伊辛模型的边缘效应
王海钦 南云程
(1.北京师范大学物理学系,北京 100875; 2.中国科学院高能物理研究所,北京 100049)
1 计算方法
VCE(variational cumulant expansion)方法,又叫变分累积展开法.基本计算过程如下:统计物理中正则系综的配分函数可以写为:
(1)

(2)
因此自由能F写成:
F=-kBTlnZ=-kBTlnZ0-kBTln
(3)
选择合适的S0使S-S0为小量则可将(3)展开为
(4)
其中:F0=-kBTlnZ0,一级近似时忽略(4)中高阶项得到
F1=F0-kBT
(5)
N个格点的伊辛模型哈密顿量为:
(6)
本文只讨论铁磁耦合(JA>0)的情况.μ0代表一个格点的磁矩,B是外加磁场.用VCE方法求解伊辛模型,试探波函数选为:
(7)

根据(7)式得:
其中NA代表A晶格上原子总数,则
F0=-kBTNAln(2coshξ).
(8)
把(6)式代入(1)式中:
根据(2)中
(9)
F1= -kBTNAln(2coshξ)-JA(tanhξ)2σA-
μ0BtanhξNA+kBTξtanhξNA.
(10)
热力学平衡时自由能取极小值,应用变分原理
(极值条件),
(11)
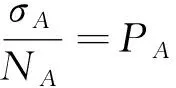
(12)
根据热力学公式,代入公式(10)得到系统磁化强度:
(13)
利用(12)和(13)两式可以计算B=0时的自发磁化.如果外场B不为0,可以得到磁化公式.为此画出外场随变分参数ξ的变化情况,如图1所示.
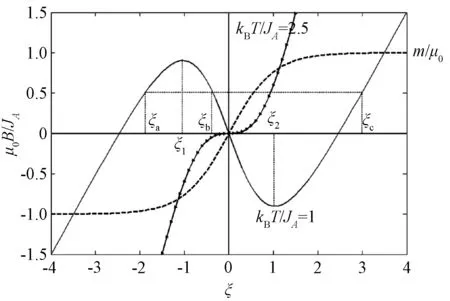
图1 磁化强度、外场随变分参数ξ的关系,取d模型, PA=2.5,kBT/JA=1,2.5

(14)
ξC=ξ1
(15)
(16)
这就是矫顽力的表达式.
利用(12)和(13)两式可得到磁化率的公式.由定义:
则系统磁化率为:

由于磁化率是在临界点之上,根据公式(12)的数学意义,因为在居里温度及其更高温度,ξ=0, 所以coshξ=1则:
(17)

2 有限二维蜂窝结构伊辛模型的数值计算
2.1 有限单层蜂窝结构的分类
根据不同的边缘结构可将蜂窝结构分为如下四种情况,分别如图2(a)、2(b)、2(c)和2(d)所示.

图2 单层蜂窝结构四种情况
如上图,以a模型(偶偶)为例,从蜂窝格子中心来看,设横向有2k个蜂窝,纵向有2n个蜂窝,这类结构,简称a模型(偶偶).其中黑点代表格点,上图中当k=1,n=2,表示横向有2个蜂窝,纵向有4个蜂窝,同理,b模型、c模型和d模型以此类推.对四种模型的最近邻对数σA、格点总数NA、平均格点配位数PA分别计算可得如下一览表.

表1 四种模型的σA、NA、PA一览表
2.2 热力学量的数值计算
利用公式(12)和(13)两式,取外场为零,数值计算得到自发磁化曲线如图3所示.首先,分析四种蜂窝模型自发磁化性质的共性.所有曲线在一定温区都有不为零的值,说明这些结构都有自发磁化.同时,对每一个结构,自发磁化都随着温度的升高而降低,最终为零,这时的温度就是临界点(即居里点).这是由于温度升高,热运动使自旋由有序趋于无序的结果[4].四种结构还有一个共同点,随着结构的增大,自发磁化都在增大,临界点也在升高,而且最终的临界点都趋于相同值3.这是由于尺寸增大造成原子数增加,处于边缘的原子数按线性规律增加,内部原子按平方规律增加,造成平均配位数增加,最终使得边缘效应小到可以忽略.这个最终临界点3正是无限大蜂窝结构的配位数,这个结果与平均场近似一致[5].
为了深入了解蜂窝模型的其他性质,我们选取d模型为研究对象.图4给出了蜂窝结构d模型在不同尺度(n=k=1、n=k=2、n=k=3和n、k为无限大)时矫顽力μ0B/JA随温度T的变化曲线.可以由图中内插图看出,当二维尺寸一定时,矫顽力随温度的升高而减小,最终为零,这时的温度正达居里点.原因是温度越高,磁化强度越小,越容易受到磁场的影响[5].温度到达居里点时,自发磁化消失,系统从铁磁相变为顺磁相,磁滞曲线的面积为0[9],矫顽力为0.此外可看到,二维尺寸越小,μ0B/JA-kBT/JA曲线越下凹,变化越快,且温度相同,二维尺寸越大时,矫顽力越大.

图3 单层有限蜂窝结构自发磁化,其中(a)、(b)、(c)、(d)分别对应图2中的(a)、(b)、(c)、(d)四种结构

图4 蜂窝结构d模型矫顽力μ0BC/JA随kBT/JA的变化,分别取n=k=1、n=k=2、n=k=3和n、k为无限大时
3 无限大二维平面与无限大圆筒形伊辛模型比较
有限大蜂窝状圆筒伊辛模型的推导和计算同二维平面一样,同样推广到无限大模型.
当模型尺寸较小时,边缘原子多.这些边缘原子的最近邻原子相对较少,当然耦合成铁磁相的“束缚力”就较小,整个系统就不稳定,自发磁化易遭破坏;当模型尺寸趋于无限大时,结构铁磁耦合较强,临界点就高.此时边缘原子比例可以忽略,边缘效应逐渐消失. 如图5显示,两条曲线高度重合,并且临界点相同.因为模型尺寸无限大时,边缘效应逐渐消失,此时圆筒就相当于一个无限大二维平面.

图5 无限大二维平面和圆筒的自发磁化
图6中曲线a是无外场的自发磁化曲线.特别值得注意的是曲线e、f和g,它们加的是反向磁场.首先看到的是,在一个温度下这些曲线可能给出两个数值,说明数学上有两个解.第一个数值表示温度升高磁化强度下降,这是合理的.另一个较低的数值显示相反的规律,这不符合物理规律,须舍弃;第二,尽管较高的数值曲线段是合理的磁化强度,但是仍被外场压制而降低了;第三,对于某一曲线,当温度升高到一定数值时,两个解重合,过了这个点就没有解了.这说明正向磁化强度没有了.曲线e、f和g对应的反向图就分别是曲线b、c和d关于温度轴的镜面反射图.换句话说,曲线e、f和g的最右端就是矫顽力.

图6 无限大二维平面和圆筒的磁化强度随外场的变化曲线,图中曲线a、b、c、d、e、f和g分别对应μ0B/JA=0、0.5、1、1.5、-0.5、-1和-1.5
利用公式(16)计算矫顽力得到曲线如图7所示.可得到二维无限大平面和圆筒的曲线高度重合,原因是两个模型在趋于无限大时,平均配位数相等,使得磁化强度被矫正的程度一样.

图7 矫顽力随温度的变化关系
当磁化强度达到饱和值时,减小磁化场,磁化强度的变化滞后于外场的变化;当外场减小到零时,磁场强度并不为零;当反向磁场增大到μ0B/JA时,磁场强度立刻减小到零,形成一支曲线.磁场减小并再反向时,得到另一支曲线,共同组成磁滞回线.而极限磁滞回线上的μ0B/JA称为矫顽力.随着温度的升高,磁滞回线宽度越来越窄.当温度在临界温度之上时,磁滞现象消失,产生的曲线呈顺磁性.当温度在临界温度之上时,铁磁体从铁磁相变成顺磁铁,发生了二级相变.因此,磁滞回线宽度消失,变成一条曲线.且两个无限大模型的磁滞回线高度重合.综上所述,无限大二维平面和无限大的圆筒模型各热力学性质基本相似.

图8 kBT/JA=1.5, 2,3时二维无限大平面和圆筒的磁滞回线
4 总 结
本文通过VCE方法,得到二维有限蜂窝结构铁磁耦合伊辛模型的自由能等各热力学量的表达式.以单层蜂窝状结构的四种模型为基础,对其自发磁化强度进行分析与比较,得到了尺寸对于热力学性质的影响规律.系统的二维限度越大,居里点越大,且不超过该晶格结构的配位数.比较了无限大二维平面和无限大圆筒模型的各热力学性质,得到无限大的二维石墨烯结构和单层碳纳米管的热力学性质基本相似.

