系泊系统在不同海况下的适应性分析与设计*
麻 云 张 霞 刘 明 盛延亮 汤镟蓉 张泽彬 刘家辰
(天津工业大学,天津 300387)
0 引 言
随着科技的发展,人类对海洋的开发利用也加快了脚步.任何形式的开发利用都离不开工程设备,如水下探测器、海底观测站、海洋平台等.所有这些设备都需要系泊定位,才能长期可靠地工作[1].近浅海观测网的系泊系统由钢管、钢桶、重物球、电焊锚链和锚组成.水声通讯系统安装在一个密封的圆柱形钢桶内.当钢桶与竖直方向角度超过一定角度时,设备工作效果较差,因此对系泊系统进行合理的设计及显得尤为重要.
某型传输节点的浮标系统可简化为圆柱体,系泊系统由钢管、钢桶、重物球、电焊锚链和特制的抗拖移锚组成,如图1所示.为保证设备的工作效果,要求钢桶的倾斜角度(相对于竖直方向)不超过5°,锚链末端与锚的连接处的切线与海床的夹角不超过16°.因此,系泊系统的设计问题就是确定重物球的质量,使得浮标的吃水深度和游动区域及钢桶的倾斜角度尽可能小.
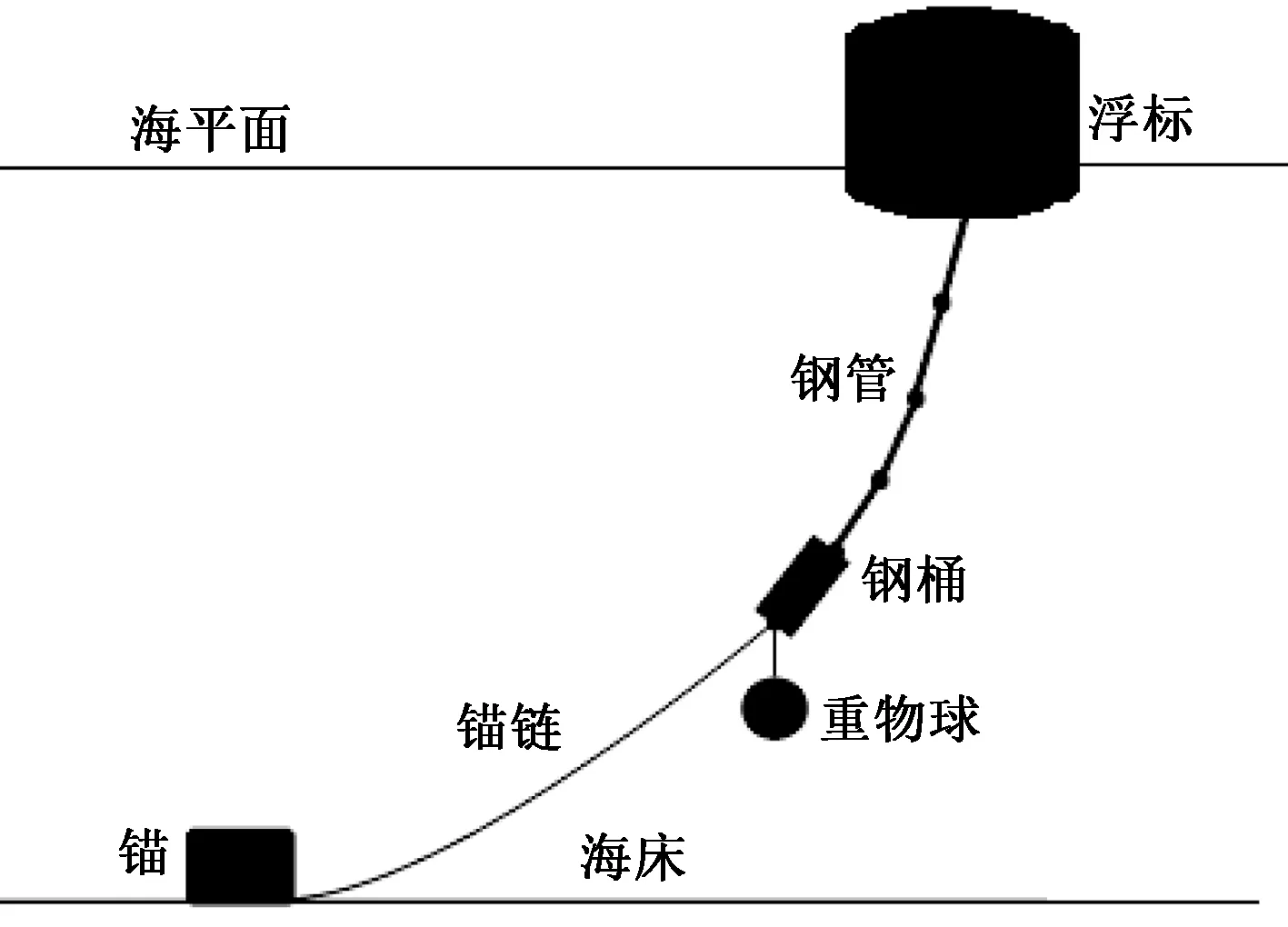
图1 水声通讯系统中系泊系统组成
1 符号说明
符号说明见表1.
2 系泊系统模型的建立
2.1 改进的悬链线方程
锚链结构复杂,形状不固定,难以直接对其进行受力分析.考虑到在对海水中锚链各参数的研究中,悬链线模型是一种被广泛用的模型,因此本文用悬链线方程对锚链进行分析,查阅文献得到一般情况下的悬链线公式如下[2]:

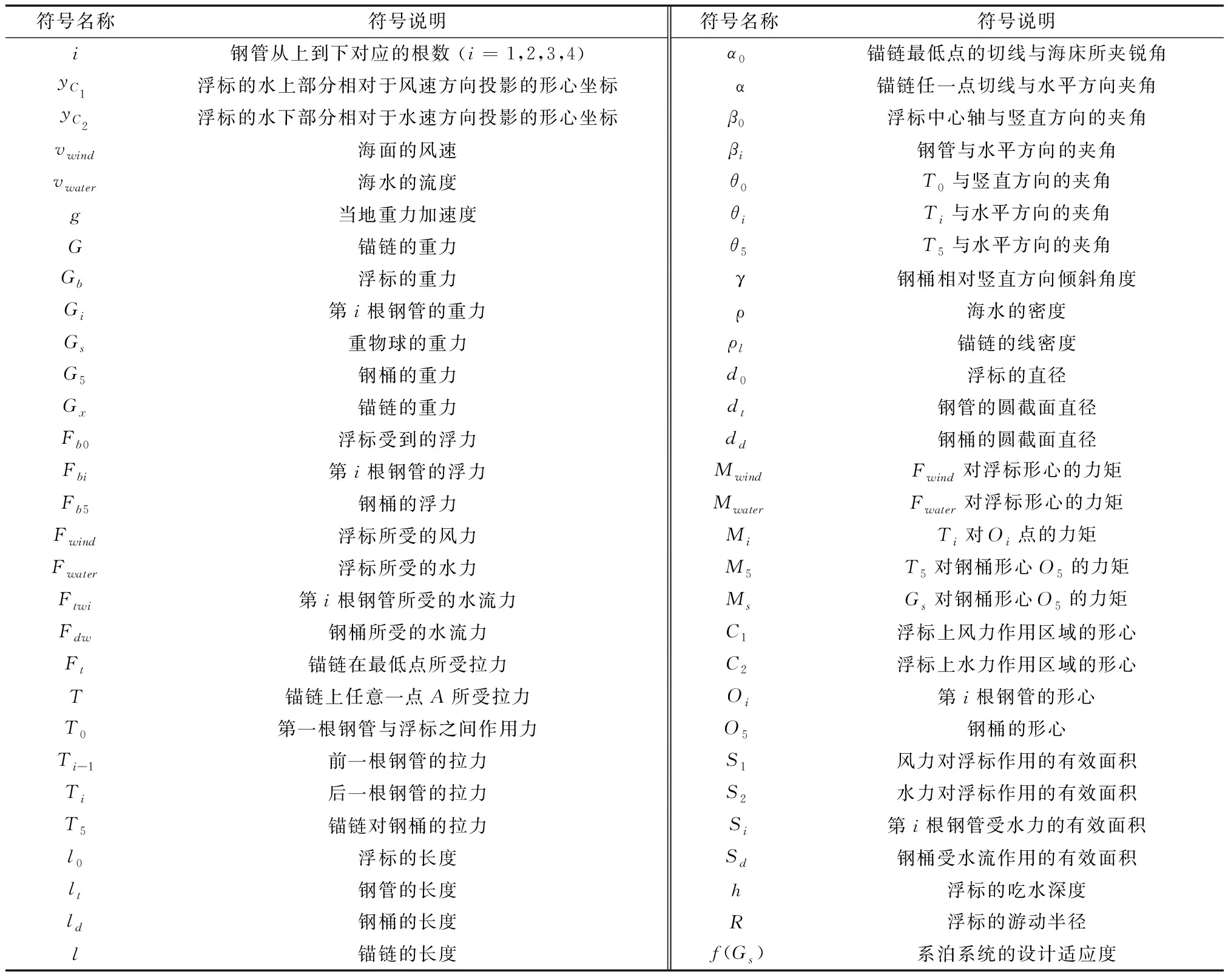
表1 符号说明
上述公式最低点受力沿水平方向,但实际中,锚链末端与锚的链接处的切线方向与海床的夹角并非一定为零度.因此,本文将对已有的悬链线模型进行改进,推导最低点为任意角度时的悬链线方程.
任取一段锚链进行分析,如图2所示,A点是锚链上任意一点,此段锚链受三个力的作用,分别有:锚链的重力G,A点所受拉力T,最低点所受拉力Ft.画出锚链力平衡示意图如图3所示.
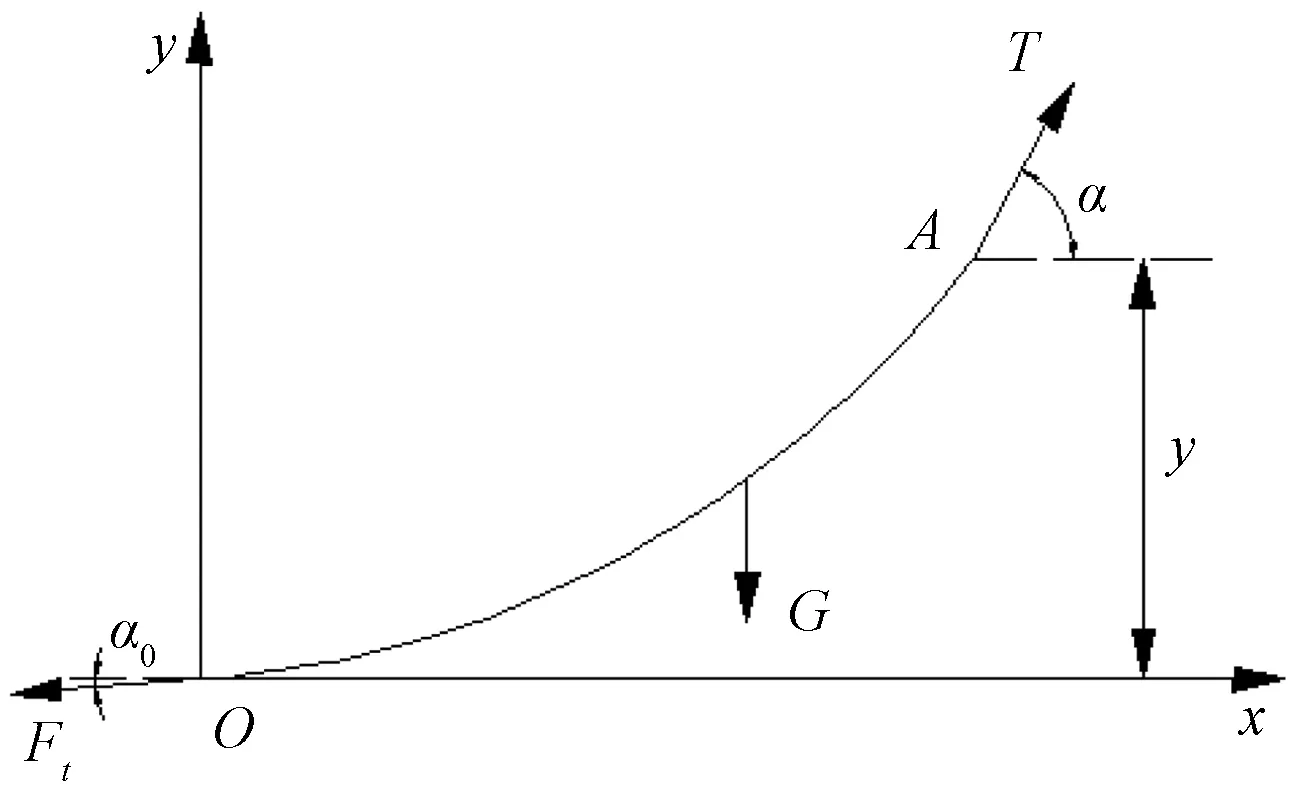
图2 悬链线受力情况
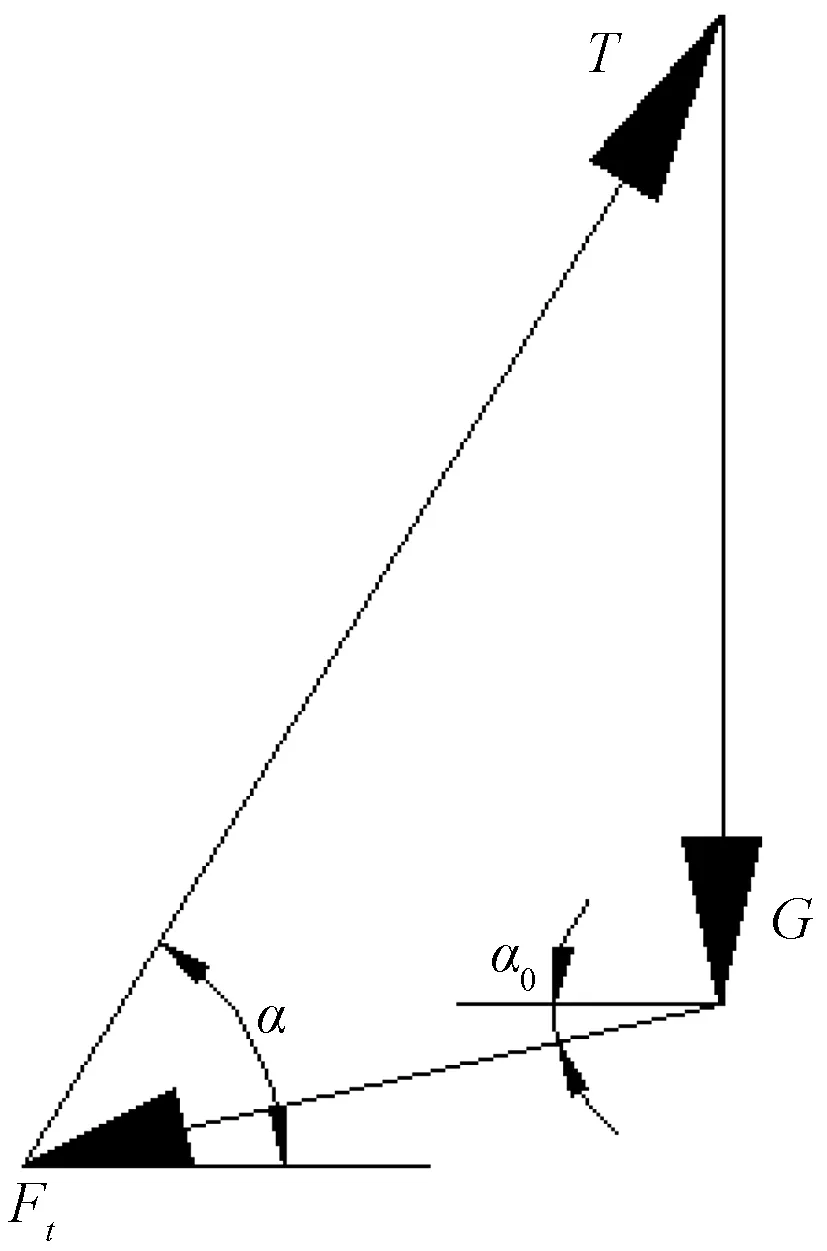
图3 锚链受力平衡示意图
对悬链线的受力进行分解,由静力学平衡条件可得:
∑Fx=0:Tcosα-Ftcosα0=0.
(1)
∑Fy=0:Tsinα-Gx-Ftsinα0=0.
(2)
由上式可得,悬链线任意一点A的斜率为:
(3)
其中,k表示锚链单位长度的质量,l表示悬链线的弧长,g表示重力加速度,α0表示所受拉力与x轴的夹角.
为导出悬链线的一般规律,消去不定量l,将式(3)两边对x求微分:
(4)
将(4)式整理,两端进行积分:
对上式进行积分得:
进行分离变量并积分,有:
于是得到悬链线上任一点的纵坐标为:
(5)
式(5)是悬链方程的一般形式,式中C1、C2为积分常数.本文中,坐标原点位于悬链线最低点,得到初始条件,当x=0时:
(6)
由式(6)可求出两个积分常数:
将C1,C2带入式(5)可得一般情况下的悬链线方程:
2.2 系统受力分析
在考虑水深、风力和水流力情况下,为了便于建模,本文做出了如下两点假设:风力、水力与海面平行;一定海域内风力和水流力保持方向不变[7].
2.2.1浮标受力分析
本文将浮标看作刚体进行分析,浮标在风力和水力的作用下发生倾斜,定义浮标吃水深度h为海平面与浮标中心轴的交点到浮标的底面圆的中心距离,如图4所示.
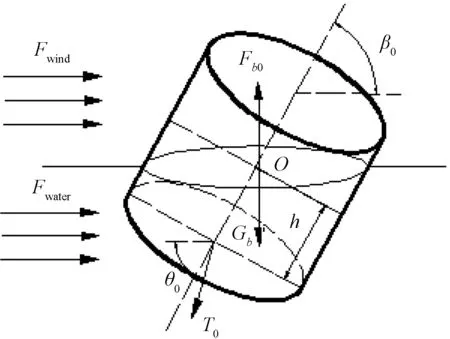
图4 浮标受力情况
如图4、5所示,Fb0表示浮标所受浮力,Gb为浮标所受重力,β0为浮标中心轴与竖直方向的夹角,T0为第一根钢管对浮标的拉力,θ0为T0与竖直方向的夹角,S1、S2分别为风力与水力作用的面积,点C1、C2分别为风力作用区域和水力作用区域的形心位置.
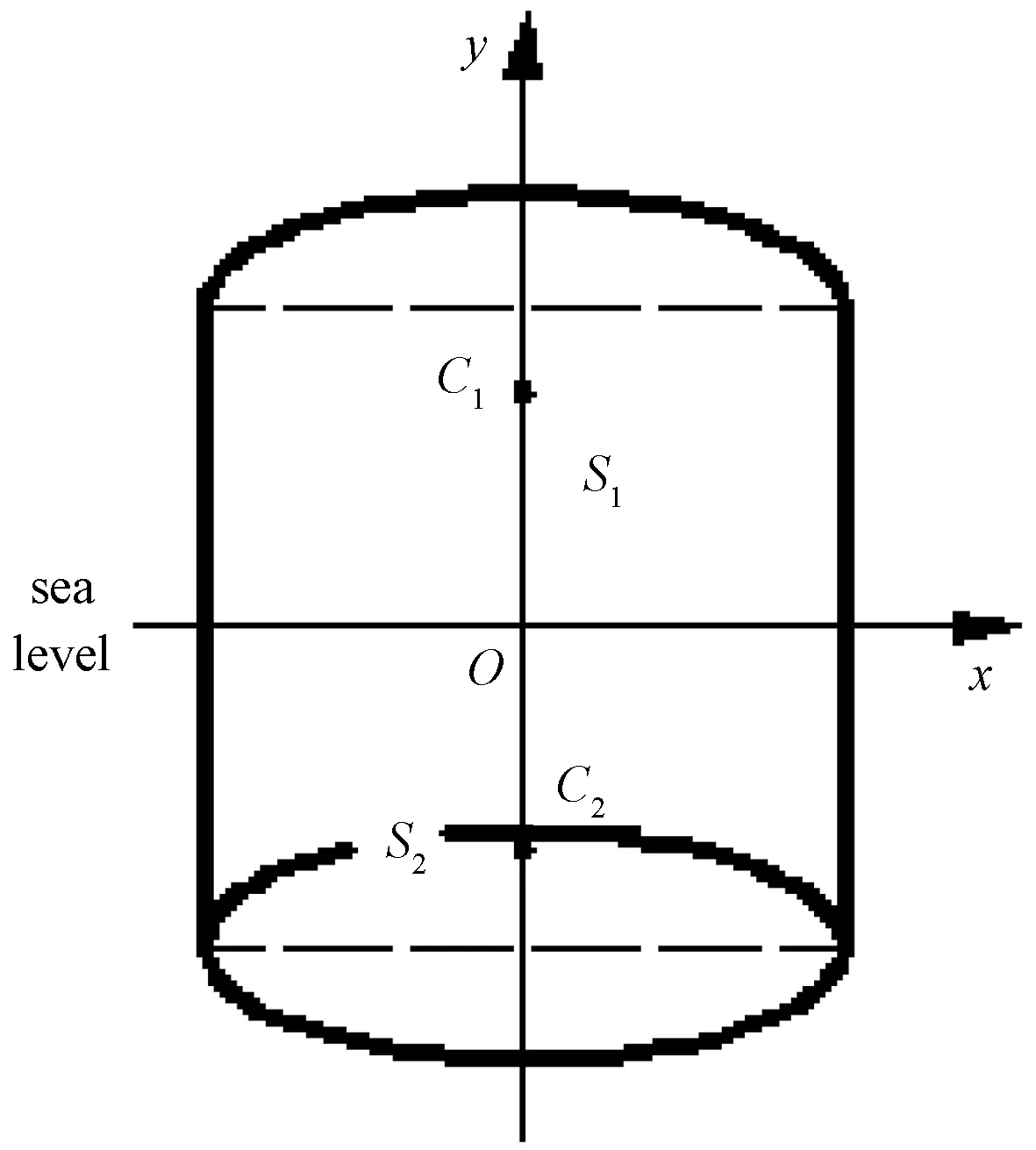
图5 浮标沿风速法向面投影示意图
1)通过浮标排开水的体积,可以求出浮标所受浮力为:
2)合力为零.通过空间变换及投影,得到侧视投影图如图5,其中风力等效作用区域为S1,水力等效作用区域为S2,计算得:
由近海风荷载近似公式(F=0.625×Sv2(N))和水流力近似公式(F=374×Sv2(N)),得风力、水流力为:
浮标在最远处平衡,其所受的合力等于零:
3)合力矩为零.浮标为刚性件,由静力学知识可得,浮标平衡不仅合力为零,合力矩也为零.区域S1,S2均关于y轴对称,故各自形心 都位于y轴上,各区域形心离O点的距离为其纵标的绝对值.
浮标在水上的部分相对于风速方向的投影为一个矩形和一个半椭圆形,可分别求出各自的形心坐标.易得矩形区域形心坐标为:
已知半圆的形心坐标为yc=2d0/3π,则将其如图倾斜角度β后,得到半椭圆的形心坐标为:
于是可得浮标在水面上的部分形心坐标为:
其中S1为半椭圆区域面积,S2为矩形区域面积.同理,可求出浮标在水下部分相对于水速方向投影的形心坐标yC2,整理后有:
浮标在水面上的面积为S1,作用在其的风力等价于相同大小的力作用在S1的形心上,则风力对浮标形心的力矩为:
Mwind=FwindyC1.
同样,可得水流力对浮标形心的力矩为:
Mwater=FwateryC2.
综上所述,可列出浮标在O点的力矩平衡方程:
∑M0=0:FwindyC1-FwateryC2-T0sin(θ0-β)=0.
(9)
4)参数求解.联立求解上述方程组(7)、(8)、(9)时,发现其中β不易求出其解析解,但可利用计算机仿真的方法,给定一个仿真误差,求出其数值解.因此设
Y=FwindyC1-FwateryC2-(Fb0-G0)cosβ+(Fwind+Fwater)sinβ,对β在之间以k为步长,ε为误差进行仿真,满足:|Y|<ε.
2.2.2钢管受力分析
将四根钢管均可看作刚体,由上到下对钢管进行排序,现对其中任意第i根(i=1,2,3,4)钢管受力分析,其受力示意图如下:
如图6所示,第i根钢管受水流力Ftwi、重力Gi、浮力Fbi、前一根钢管的拉力Ti-1以及后一根钢管的拉力Ti,βi表示钢管相对于水平方向的倾斜角度,θi-1、θi分别表示Ti-1、Ti与水平方向的夹角,Oi点表示钢管的形心.
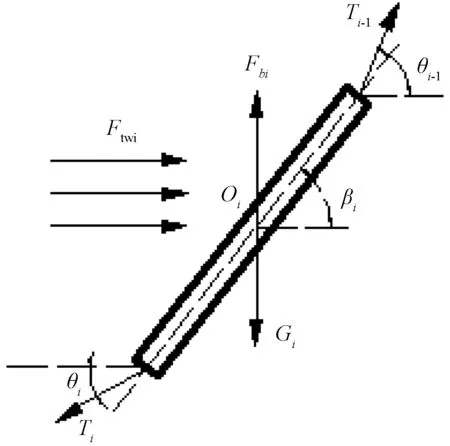
图6 钢管受力示意图
1)通过钢管排开水的体积,可求得钢管所受浮力:
2)合力为零:因钢管端面面积较小,故可忽略端面水流力影响,水流作用在第i根钢管上的有效面积为:
Si=dtltsinβi.
由近海水流力近似公式,得钢管所受水流力为:
钢管平衡时,所受的合力等于零:
“鲜满天下仍未已”,为此太太乐一直在不断努力与前进!10月,太太乐不仅举办了享誉全球的第六届鲜味科学与品质生活国际鲜味研讨会,同时为培养鲜味人才,发展鲜味事业,举办了首届太太乐全国鲜味科学知识竞赛,赛事轰动。同期10月15日晚上21:17,由太太乐联合推出的大型美味科学人文记录片《鲜味的秘密》在央视7套与观众见面。鲜味之旅,邀你同行!
3)合力矩为零:同浮标一样,钢管也为刚性件,平衡时不仅合力为零,合力矩也为零.水流力均匀作用在每根钢管上,易知水流力对钢管形心Oi的力矩为零.上一根钢管的拉力Ti-1对Oi点的力矩为:
同样,可得下一根钢管的拉力Ti对Oi点的力矩:
结合静力学知识,可列出钢管在形心Oi点的力矩平衡方程:
(12)
综上,可得
2.2.3钢桶受力分析
当钢桶与竖直方向的倾斜角度超过5°时,设备工作效果较差.现对钢桶进行分析,受力示意图如下:
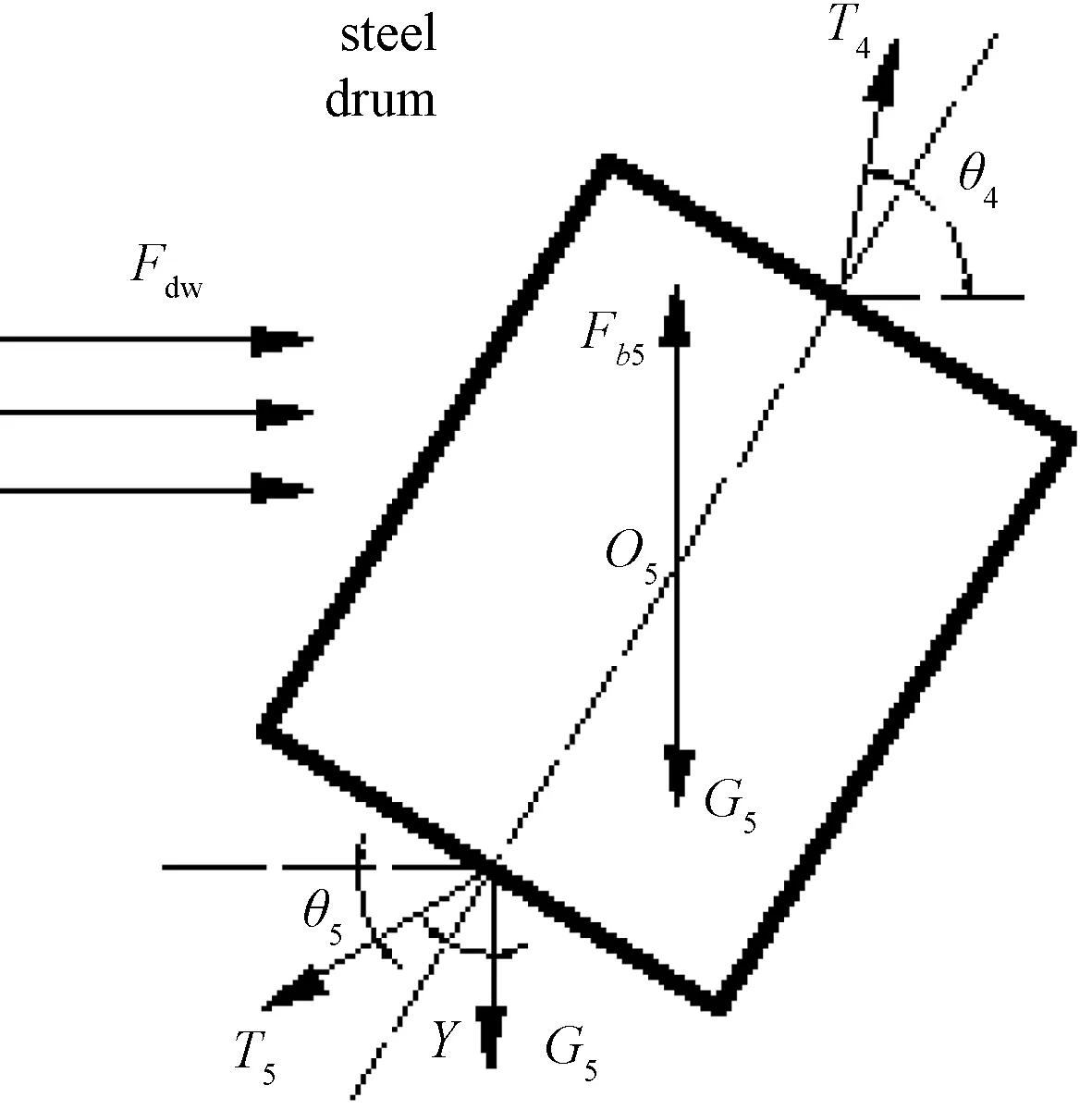
图7 钢桶受力示意图
如图7所示,钢桶受水流力Fdw、重力G5、浮力Fb5、重物球拉力Gs、前一根钢管的拉力T4以及锚链的拉力T5,γ表示钢桶相对于竖直方向的倾斜角度,θ4、θ5分别表示T4、T5与水平方向的夹角,O5点表示钢桶的形心.
1)合力为零:钢桶所受水流力为作用在钢桶壁及钢桶端面上水流力的合成.根据图6,可求得钢桶所受水流的等效作用面积为:
由近海水流力近似公式,得钢管所受水流力为:
钢桶平衡时,所受合力为零:
2)合力矩为零:同浮标一样,钢管也为刚性件,平衡时不仅合力为零,合力矩也为零.钢管对钢桶的拉力T4对钢桶形心O5的力矩为:
同样,锚链对钢桶的拉力T5对钢桶形心O5的力矩为:
重物球的拉力Gs对钢桶形心O5的力矩为:
结合静力学知识,可列出钢桶在形心O5点的力矩平衡方程:
(15)
综上可得
2.3 系统约束条件及目标函数
2.3.1不等式约束条件
上述(1)~(15)式反应了系泊系统在不同海况下的工作特性,也是系统的等式约束条件.
为保证设备工作效果,钢桶的倾斜角度(钢桶与竖直线的夹角)需要小于5°.同时,锚链在锚点与海床的夹角不超过16°,否则锚会被拖行,致使节点移位丢失:
考虑近浅海的海风、海水实际速度,有如下约束:
在一定范围内增加重物球的质量,能够增加系统的稳定性,但系统的总重力不能超过系统所受到的浮力:
2.3.2目标函数
在风力和水流力等因素共同作用下,以锚为圆心,浮标的游动半径为:
在设计系泊系统时,改变重物球质量,可调节系泊系统的各项指标.在设计时,应使浮标的吃水深度和游动区域以及钢桶的倾斜角度应尽可能小,于是得:
为了求解这一多目标问题,本文首先利用计算机仿真,改变重物球质量Gs,得到关于h、R、γ的三组仿真数据,并对每组数据采用极差正规化,去除每组数据的量纲:
之后利用线性加权法,将多目标问题转化为单目标.再对目标函数取倒数,并定义其为设计此类系泊系统的适合度:
在设计时,设计者可调节重物球的质量,改变系统的各项参数,使得其设计的适合度达到最大.
3 实例分析
为进行应用验证,考察模型的适用情况,本文选取了具有较强代表性的海况进行分析:风速为36 m/s,水流速度为0 m/s,水深18 m.为得到重物球的质量对设备工作情况的影响,本文对重物球质量进行仿真,得到如下曲线:

图8 钢桶倾斜角度变化曲线
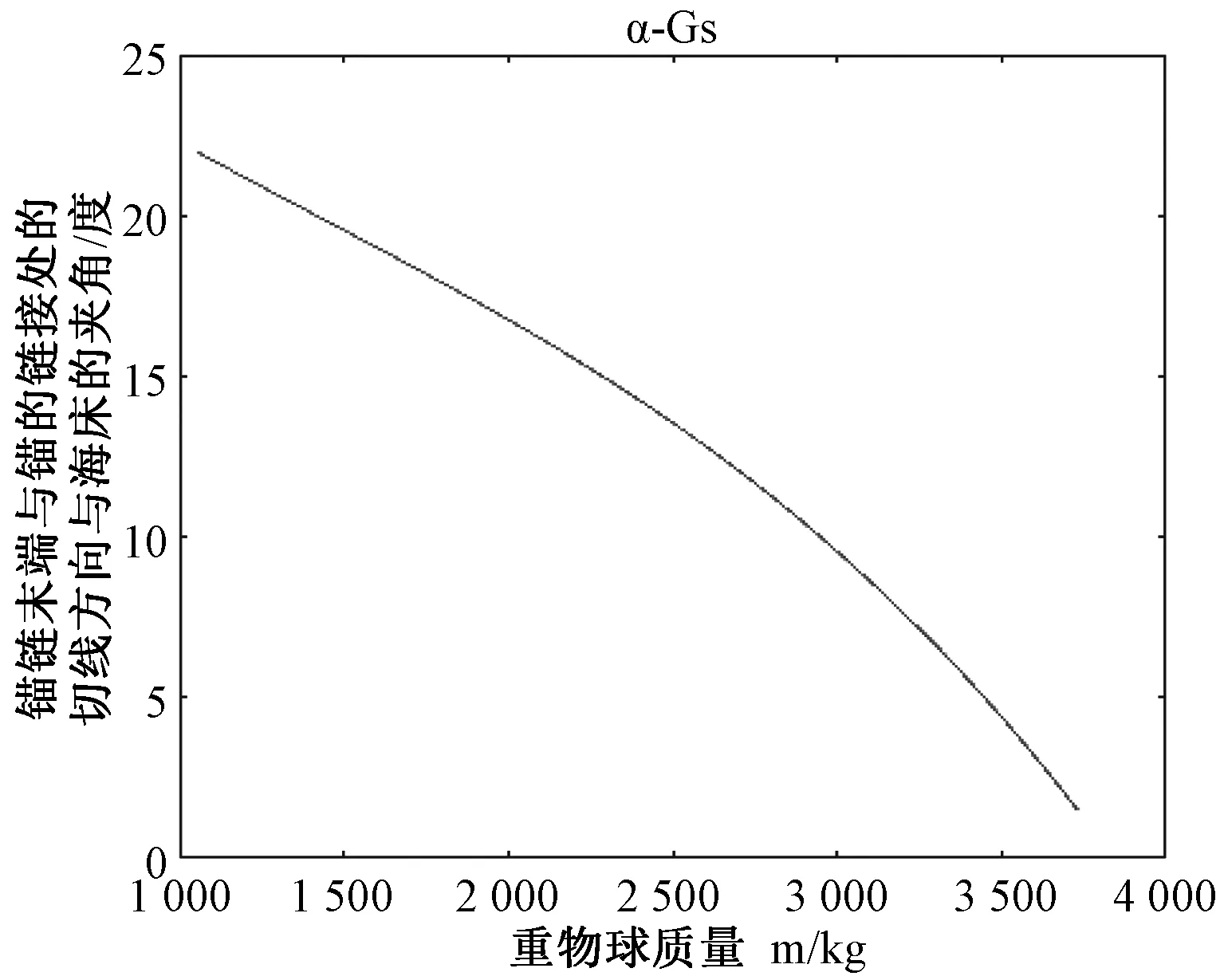
图9 锚链在锚点的切线与海床夹角变化曲线
从图中可以看出钢桶倾角γ、锚链末端与锚的链接处的切线方向与海床的夹角α0与重物球的质量ms呈现明显的反比关系.因而存在重物球的临界质量mmin,使得钢桶倾角γ<5°,锚链在锚点的切线与海床的夹角α0<16°.
利用计算机仿真,得出在此海况下,满足设备工作要求的重物球最小质量,其结果如下表格:

表2 仿真结果

同时,为了寻找在此海况下使系泊系统设计适合度最大的重物球的质量,将仿真得到一系列关于h、R、γ的三组仿真数据极差正规化,去除每组数据的量纲,整合成单目标规划后,取权重分别为0.1、0.4、0.5,得到适应度与重物球质量关系图如下:
如图10,当重物球质量为3 095.19 kg 时,在此权重下的设计适合度为2.044 9且达到最大,此时有锚链方程:
y=20.800 9cosh(0.048 1x+0.153 1)-21.045 3.
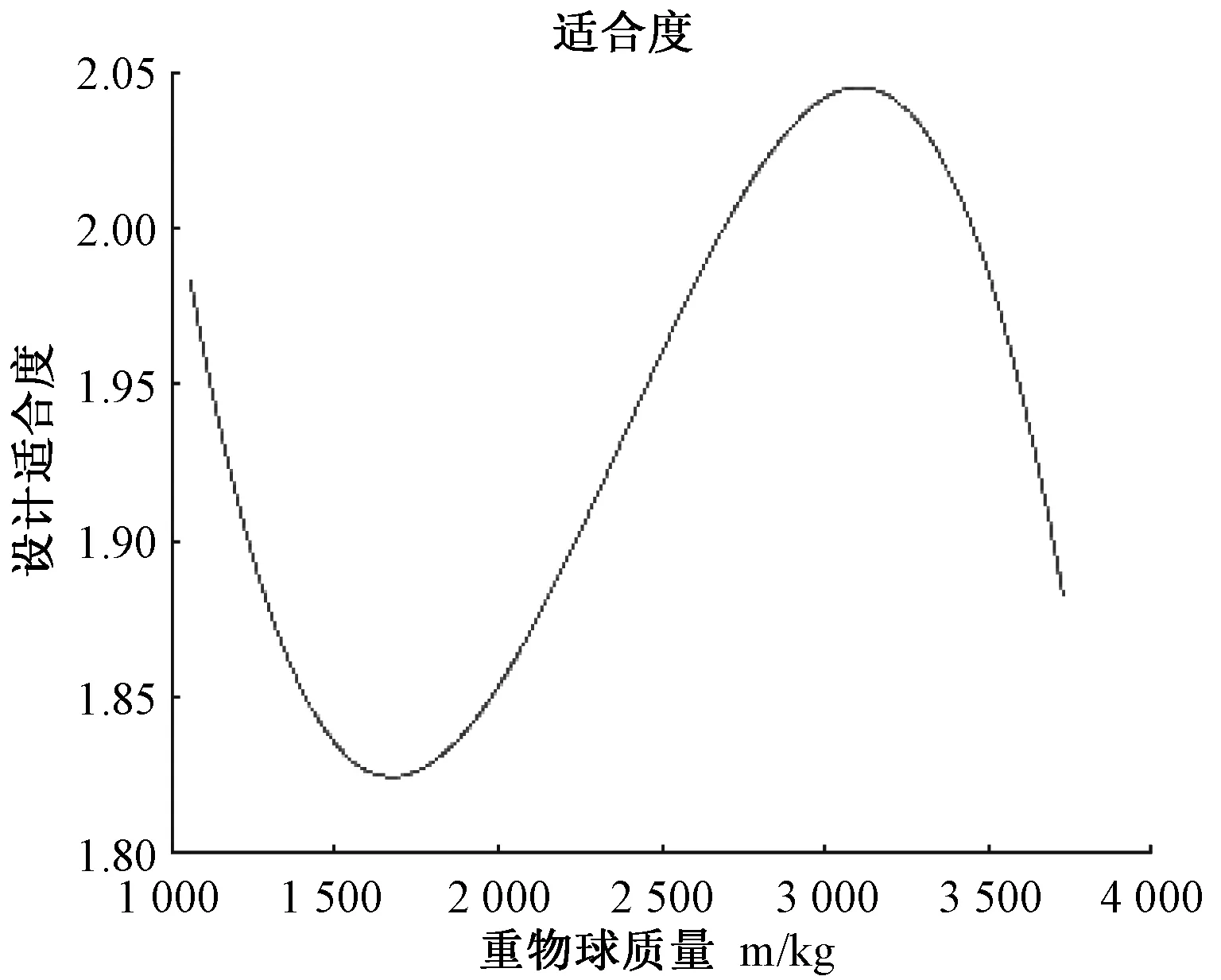
图10 锚链在锚点的切线与海床夹角变化曲线
得到锚链形状图像(图11):

图11 锚链形状
此时,浮标的吃水深度为1.345 1 m;钢管相对于水平方向的倾斜角度由上到下依次为87.496 9°、87.490 9°、87.484 8°、87.478 8°;钢桶倾斜角度为3.559 9°;浮标游动区域半径为19.363 9 m.
3 结 语
系泊系统在海洋中的工作状况是多变的,可根据不同的环境需求,修改参数本文实例中的海风速度、水流速度以及水深等参数,调节重物球质量,保证系统在不同海况下的稳定工作.

