阶次跟踪能量算子与奇异值分解结合的滚动轴承故障诊断

江志农，胡明辉，冯坤，贺雅

(北京化工大学 诊断与自愈工程研究中心，北京 100029)

振动分析是滚动轴承状态监测的主要方法，轴承故障产生的振动信号通常是瞬态、非平稳的，并且受到高频载波信号调制[1-2]，对其直接应用传统的包络解调容易产生“频谱模糊”现象[3-4]，无法有效提取故障特征。能量算子能有效分析具有时变幅值和时变频率特征的振荡信号[5-7]，并且计算复杂性小，精度高；阶次跟踪方法[8]则可对时域上的非平稳信号进行等角度重采样，从而得到角域上的准平稳信号。

同时，轴承故障初始阶段引起的振动通常为微弱振动信号，其冲击特征常湮没于机械系统大量干扰源产生的背景噪声中，提取故障特征时有必要对信号进行降噪处理。奇异值分解(Singular Value Decomposition，SVD)能够对噪声混杂信号中的有用部分进行有效、可靠地估计，且基于SVD的降噪方法计算量小，在信噪比较低的情况下仍然能够分离有用信息与噪声信号，特别适合轴承振动加速度信号的降噪[9-10]。

因此，针对滚动轴承变速运行过程中的时域振动信号，提出了将阶次跟踪能量算子与奇异值分解相结合的滚动轴承故障诊断方法，以有效提取滚动轴承的故障特征。

1 奇异值分解降噪

设A为实信号X通过变换所得到的m×n阶实矩阵，其满足

A=UΛVH，

(1)

式中：U，V分别为m×m，n×n阶正交矩阵；Λ为m×n阶对角矩阵，其所有的对角元素非负且降序排列，这些对角元素即为信号矩阵A的奇异值。实践表明，所测信号的信噪比越大，矩阵Λ对角线上的零值元素数量越多。根据矩阵Λ对角线上零值元素的数量可近似估计出信号的信噪比。基于该理论发展而来的SVD降噪技术[11]为：首先，将矩阵Λ中奇异值很小的元素置零，构造一个新的矩阵Λ′；然后，根据(1)式重新计算得到实矩阵A′,并推导出降噪后的信号。

2 阶次跟踪能量算子

阶次跟踪能量算子(Order Tracking Energy Operator，OTEO)是能量算子(EO)在角域上的应用，是对EO的改进和完善，可用于变工况下滚动轴承的微弱故障特征提取。

2.1 阶次跟踪

阶次的定义是旋转机械轴每转发生振动的次数。也就是说阶次相对于转速是无关的，故障频率是转频的某一阶成分。阶次的定义为

(2)

式中：O为阶次；n为轴的转速，r/min；f为故障频率，Hz。

阶次分析的关键在于等角度采样，实质上是等角度时刻的获取，得到等角度采样时刻后在原函数上插值拟合即可得到角域上的平稳信号[12]。

2.1.1 重采样

采用多相FIR滤波器对振动信号原始波形进行重采样，提高采样频率，防止在等角度采样时发生频率混叠[13]。

提高采样频率的重采样相当于在原始信号上插值。如图1所示，信号x(n)的采样频率提高L倍，得到v(n)，也即在x(n)每相邻的2个点之间插入L-1个0，设计低通滤波器h(n)对v(n)进行低通滤波，从而得到插值后的输出y(n)。

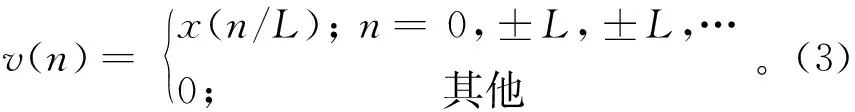
图1 插值滤波流程图Fig.1 Flow chart of interpolation filtering

2.1.2 获得等角度序列

由转速趋势得到各采样点对应旋转过的角度，找出角度最小值及最大值，根据每转上采样点数是最大预分析阶次的2倍生成等角度序列，即当转轴经过这些等角度点时进行采样[14]。

设原采样间隔为Δt，第k个采样点i转速为vi，则对应的转角为

(4)

则采样点对应时刻ti=kΔt时的转轴转角为

(5)

得到t1-ti内等角度采样点数为

(6)

式中：M为预分析最大阶次，由等角度重采样定理得每转上采样点数为2M，即角域的采样频率。根据采样定理，M应满足

(7)

式中：nmax为采样时间内轴的最大转速；fs为原始振动信号的采样频率。综上可得等角度序列为

(8)

2.1.3 二次插值

插值是指已知2组数据之间的对应关系，得出关心的非采集得到的数据对应的变量值。在此采用分段线性插值方式，这种拟合方式认为2个样本点之间符合一次函数(y=ax+b)的关系，将两点直线连接起来，已知两点之间的因/自变量就可以得到对应的变量。如图2所示，各样本点之间的时间间隔为Δt，在样本点之间以等角度间隔Δθ插值，得到等角度采样时标Tn。

图2 插值得到等角度采样时间Fig.2 Equal angle sampling time after interpolation

在重采样之后的振动信号上以等角度采样时标插值拟合后，就得到了角域上的平稳信号，实现转速无关化，按照转速趋势实现等角度重采样的流程如图3所示。

图3 等角度重采样流程图Fig.3 Flow chart of equal angle resampling

2.2 阶次跟踪能量算子

对于调幅调频信号x(t)，其能量算子定义为

(9)

则x(t)的振幅包络信号为

(10)

通过能量算子的运算可求得加速度信号的振幅包络信号，对包络信号进行FFT分析即可得到包络频谱[15]。对于滚动轴承故障信号而言，包络信号|a(t)|的频率成分主要为轴承故障特征频率fF及其谐波[16]，即|a(t)|是否平稳取决于fF是否为一个固定值。对于通常外圈固定、内圈旋转的轴承，其不同元件的故障特征频率可简化为[17]

fF=anr，

( 11)

式中：a为常数；nr为轴承内圈转速。由(11)式可知,轴承故障特征频率与转速成正比。在稳定工况下运行时，轴承故障特征频率为一固定值，对|a(t)|做FFT分析即可提取出故障特征。而在变工况下运行时，轴承故障特征频率随转速发生变化，直接对|a(t)|进行FFT分析会产生频谱模糊现象。

为了消除转速对特征频率的影响，在FFT分析之前先对|a(t)|进行阶次跟踪处理，得到角度域的平稳信号|a(r)|，然后再进行FFT分析得到阶次域包络频谱，该频谱包含轴承故障特征且实现了与转速的无关化。

综上所述，针对变工况引起的能量算子解调信号非平稳问题，定义阶次跟踪能量算子，其实现步骤如下：

1)根据(10)式对变工况下时域振动信号进行基于EO的分析，得到包络信号|a(t)|；

2)对时域非平稳信号|a(t)|进行阶次跟踪分析，得到角度域平稳信号|a(r)|，实现由非平稳信号向角度域上准平稳信号的转换；

3)对|a(r)|进行FFT分析，得到阶次域的包络频谱，解决由直接对非平稳信号进行FFT分析带来的频率模糊问题。

根据OTEO提取出的滚动轴承故障特征阶次，在一定程度上解决了变工况造成的频谱模糊问题，可实现变工况下滚动轴承的故障特征提取。

3 SVD与OTEO结合的诊断方法

阶次跟踪能量算子解决了滚动轴承故障特征提取中包络及变工况引起的频谱模糊问题,然而，工程中采集的轴承座加速度信号通常成分较复杂，直接对其进行包络分析效果较差，需要在包络分析之前进行降噪处理[18]。因此，提出将阶次跟踪能量算子与奇异值分解相结合的滚动轴承诊断方法，其流程如图4所示。

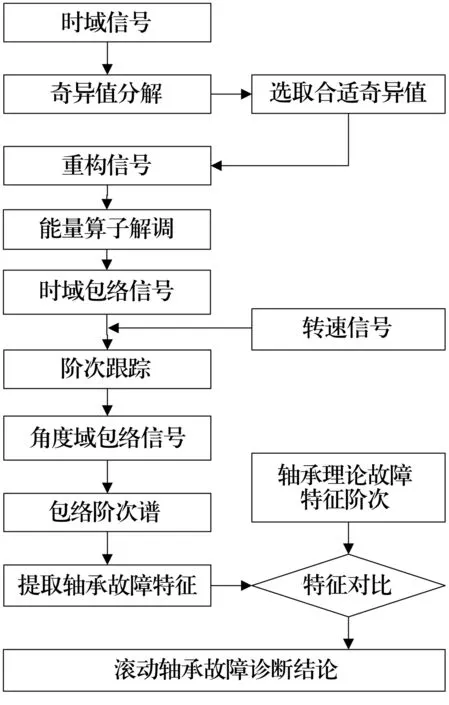
图4 基于OTEO与SVD算法的流程图Fig.4 Flow chart of algorithm based on OTEO and SVD

4 故障诊断实例

4.1 试验介绍

轴承故障模拟试验台如图5所示。试验预置1#轴承(圆柱滚子轴承)为故障轴承，在其内圈滚道面加工一条宽、深均为1 mm的槽以模拟轴承内圈故障。由故障轴承基本参数(Dw=8 mm，Dpw=125 mm，Z=34)计算可得轴承内圈故障特征频率对应阶次为18.088。由于1#轴承缺乏与其直接连接的轴承座，振动响应需经过轴系传递到相邻轴承(2#轴承)，再经过薄壁复杂路径传递到测点位置。信号受传递路径和工作环境影响，在传递过程中大量衰减并混入噪声，在测点得到的轴承故障特征信号相对于噪声极其微弱。

图5 轴承故障模拟试验台Fig.5 Test rig for bearing fault simulation

数据采集设备为LMS SCADAS振动测试系统，加速度传感器型号为BK 4519，键相传感器为接近开关。在内圈转速由737 r/min升至827 r/min的过程中(图6)采用加速度传感器和接近开关采集数据。变速过程中滚动轴承的故障信号时域波形如图7所示(图中g为重力加速度，取9.8 m/s2,下同)，从图中可以看出，时域信号呈现出非平稳特征，应用传统包络解调方法容易产生如图8所示的频谱模糊现象。

图6 转速趋势Fig.6 Trend of rotational speed

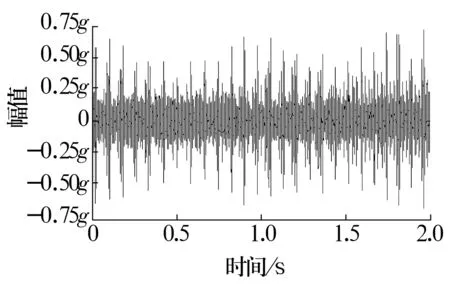
图7 振动加速度信号波形Fig.7 Signal waveform of vibration acceleration

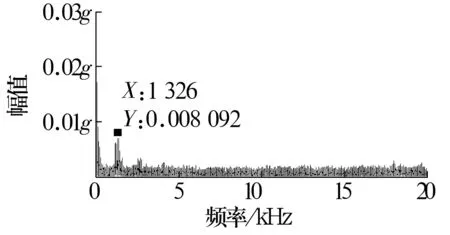
图8 转速变化引起的频谱模糊现象Fig.8 Spectrum amgibuity phenomenon caused by varied rotational speed

4.2 OTEO与SVD结合的分析方法

首先，利用SVD对原始信号进行降噪，结果如图9所示，从图中可以看出，经过SVD降噪后，原始振动信号中与轴承故障无关的冲击成分已经得到了大幅衰减。然后，对降噪后信号进行基于阶次跟踪的包络解调，得到降噪后角域信号的包络波形如图10所示。最后，进一步处理得到的包络阶次谱如图11所示，谱图中清晰可见18.09阶次及其谐波，与轴承内圈故障特征阶次18.088吻合。

图9 SVD降噪后的振动波形Fig.9 Vibration waveform after SVD denoising

图11 降噪后信号得到的包络阶次谱Fig.11 Envelope order spectrum obtained by denoised signal

为对比OTEO与SVD相结合方法的优势及合理性，选取不同算法对图7信号进行分析，结果如图12和图13所示。对比分析可知：单独进行OTEO或SVD处理的效果均不佳，特征频率完全被噪声湮没，无法提取出轴承内圈故障特征，说明OTEO与SVD相结合对于变转速工况下轴承故障的识别十分有效。

图12 基于阶次跟踪和小波降噪的Hilbert包络阶次谱Fig.12 Hilbert envelope order spectrum based on order tracking and wavelet denoising

图13 基于SVD降噪的EO包络阶次谱Fig.13 EO envelope order spectrum based on SVD denoising

5 结束语

针对实际应用中滚动轴承故障信号强干扰导致的信噪比低及变工况下故障特征提取中的频谱模糊问题，选取SVD进行降噪处理，突出冲击特征，然后采用OTEO克服变工况引起的频率模糊问题，获得可用于轴承故障识别的包络阶次频谱，并成功提取出变工况运行滚动轴承的微弱故障。

该方法虽然在研究时考虑了工程化应用的因素，但仍缺乏企业现场数据的进一步验证，下一步会采集更多数据用于该方法的实际验证，以最终服务于工程问题。