改进Laplace小波字典在轴承故障诊断中的应用

李景乐，谢馨，王华庆

(北京化工大学 机电工程学院，北京 100029)

稀疏分解与稀疏表示的理论由MALLAT提出，并广泛应用于故障诊断领域[1]。稀疏表示方法中合适的原子及字典结构能够极大地提升字典构造和稀疏表示的效率。滚动轴承的局部故障会产生周期性的冲击，从而在其振动信号中表现出周期性的瞬态冲击成分，轴承故障引起的瞬态冲击一般表现为周期振荡的指数衰减形式[2]。文献[3]提出了Laplace小波的数学表达式并验证其对故障冲击特征提取的有效性。文献[4-5]将相关滤波法结合Laplace小波运用于滚动轴承的故障诊断，有效地提取出了滚动轴承故障特征，充分验证了基于Laplace小波原子库的稀疏表示方法在滚动轴承故障诊断中的可行性。然而，通过传统相关滤波法构造的过完备原子库必须涵盖相位、阻尼系数及衰减频率信息，字典的规模异常庞大，导致运算速度缓慢甚至算法无法运行。

综上所述，采用一种新的字典构造方式，通过改进的相关滤波法选取合适的Laplace原子，并经过Toeplitz矩阵拓展构造完备字典；稀疏系数的求解则选用优化的正交匹配追踪算法(Orthogonal Matching Pursuit, OMP)。通过相关滤波筛选阻尼和振荡频率，以及字典中的原子表示相位，在缩减字典规模的同时，可以更直观和准确地找到合适的原子，得出稀疏系数能直接体现冲击的相位，从而准确地提取出故障特征频率。

1 稀疏表示及Laplace字典构造原理

一维信号的稀疏表示模型可以表示为

y=D×x+ε，

(1)

式中：y为N×1维的原信号；D为N×N维的字典；x为N×1维的稀疏系数；ε为N×1维的噪声信号[1]。

恒定转速下，滚动轴承的局部故障通常会引起周期性的冲击，一般表现为周期性的单边振荡衰减波形。Laplace小波是一种单边振荡衰减的复指数小波，比较符合滚动轴承的冲击形式，考虑到滚动轴承的振动信号为实信号，故将Laplace小波的实部作为稀疏表示的特征原子，Laplace小波实函数的数学表达式为

(2)

式中：A为归一化小波函数的系数；f为振荡频率；ζ为阻尼系数。

Laplace小波与冲击信号特征相似，所以两者的相关系数高，而Laplace小波与噪声及其他信号的相关系数低，找到合适的Laplace小波就能够准确的识别冲击信号。因此，提出基于自适应相关Laplace字典的构造方法，构造出能较好表达滚动轴承故障特征的字典，并且运用高效的OMP算法[6]从原信号中提取能够表示冲击特征的稀疏系数，并通过提取的稀疏系数进一步分析信号的故障信息。算法的具体流程如下(图1)：

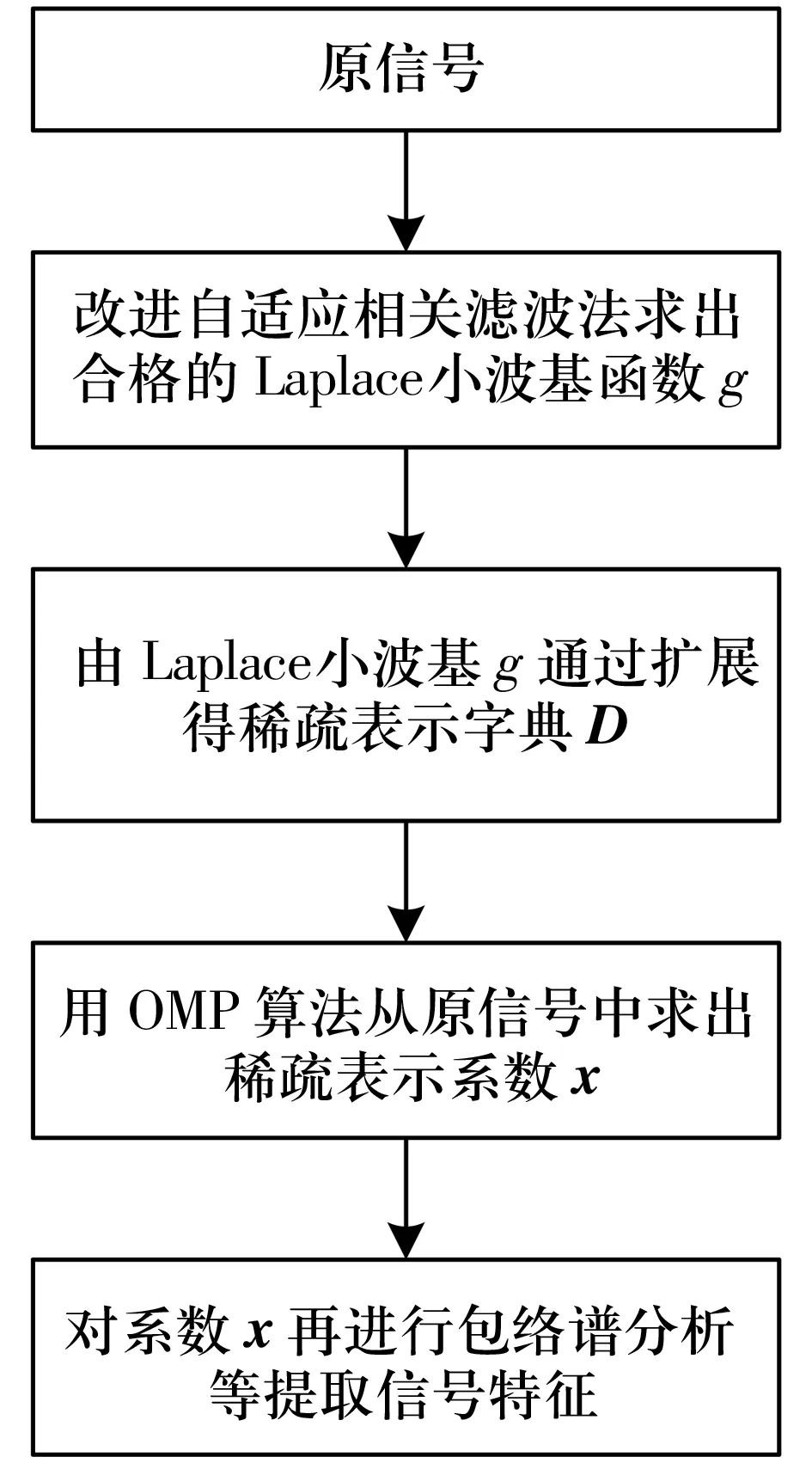
图1 改进Laplace小波字典方法流程图Fig.1 Flow chart of improved Laplace dictionary

1)截取适当长度的轴承振动信号，通过快速Fourier变换寻找可能的振荡衰减频率范围，由经验确定阻尼参数的范围，在此选定原子长度为1/10的信号长度；

2)分别设定振荡频率增量Δf及阻尼参数增量Δζ，得到变量范围内的m个频率值和n个阻尼系数值，代入小波表达式中得到m×n个不同的Laplace小波，并对每个小波做能量归一化处理；

3)分别求取这些小波与原信号的互相关函数，记录每组互相关函数的最大值；

4)取出步骤3记录的所有最大峰值中的最大值，其对应的频率及阻尼系数即为与原信号最相关的Laplace小波的参数；

5)由步骤4得到的参数构造Laplace小波原子，并展开成Toeplitz矩阵，此矩阵即为稀疏表示的完备字典，且其特殊的字典构造使其每一列即对应原信号中冲击的一个相位；

6)通过高效OMP算法求出原信号在完备字典下的稀疏表示，稀疏表示系数的个数可由经验选取，一般选取2的整数次幂；

7)通过上述步骤得到的稀疏系数对原信号进行进一步包络谱分析等处理。

2 仿真信号验证

构造仿真信号的表达式为

y(t)=A0e-πfnζ(t-kτ)×

式中：A0为幅度参数；fn为振荡频率；ζ为衰减阻尼系数；τ为冲击时间间隔；k为整数。

仿真信号幅值参数为5，振荡频率为3 000 Hz，衰减阻尼系数为0.1，假设采样频率为100 kHz，总时间为0.1 s，并且加入信噪比为10 dB的高斯噪声，冲击时间间隔为0.01 s，即仿真信号冲击特征频率为100 Hz，通过以上参数共同构造仿真信号，其时域波形及包络谱如图2所示。从仿真信号的时域图可以看出，冲击峰值被噪声淹没，无明显冲击特征，而包络谱中也无法准确识别冲击特征频率。采用上述算法对原信号进行处理，振荡频率区间设定为[1 000，5 000]Hz，Δf为50 Hz，阻尼系数区间设定为[0.01，0.3]，Δζ为0.01，稀疏系数个数设定为16，原子长度0.01 s；计算得到最适应于原信号的Laplace原子参数振荡频率为3 100 Hz，阻尼系数为0.1，基本符合原信号冲击特征参数，稀疏表示结果如图3所示。

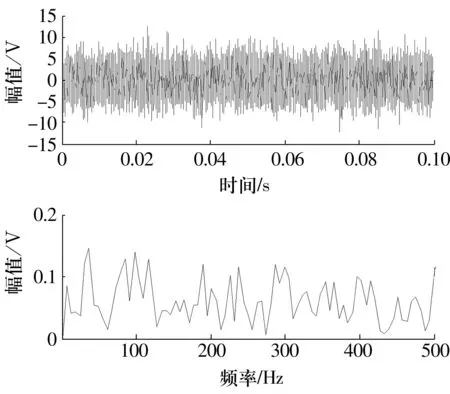
图2 仿真信号的时域波形及其包络谱Fig.2 Time domain waveform and its envelope spectrum of simulation signals

图3 仿真信号的稀疏系数及其包络谱Fig.3 Sparse coefficient and its envelope spectrum of simulation signals

从图3可以看出，从原信号中提取的稀疏系数能够比较准确地从信号中提取冲击成分，提取出的冲击频率为101.5 Hz及其倍频，与预设特征频率100 Hz相符，验证了改进算法的可行性。

3 实际验证

为进一步验证改进算法的实用性和可靠性，采用故障试验台对NTN 204型轴承进行故障试验，利用线切割在轴承内圈滚道上加工一个宽0.7 mm、深0.25 mm的凹槽，在轴承外圈滚道上加工一个宽0.3 mm，深0.05 mm的凹槽，分别模拟内、外圈故障。通过恒转速900 r/min的主轴驱动试验台，采用加速度传感器采集振动信号，采样频率为100 kHz。任意截取一段内、外圈故障振动信号，利用改进算法进行分析处理。

3.1 外圈故障特征提取

所截取轴承外圈故障信号的时域波形如图4所示。对原信号进行快速Fourier变换频谱分析，得出冲击振荡衰减频率峰值在23 000 Hz左右，依据试验信号特征及多组试验信号处理过程的参数总结，设定振荡频率范围[21 000，25 000]Hz，Δf为50 Hz，阻尼系数范围[0.01，0.3]，Δζ为0.01，稀疏系数个数设定为32，原子长度0.01 s。改进算法得到的稀疏系数及其包络频谱如图5所示。

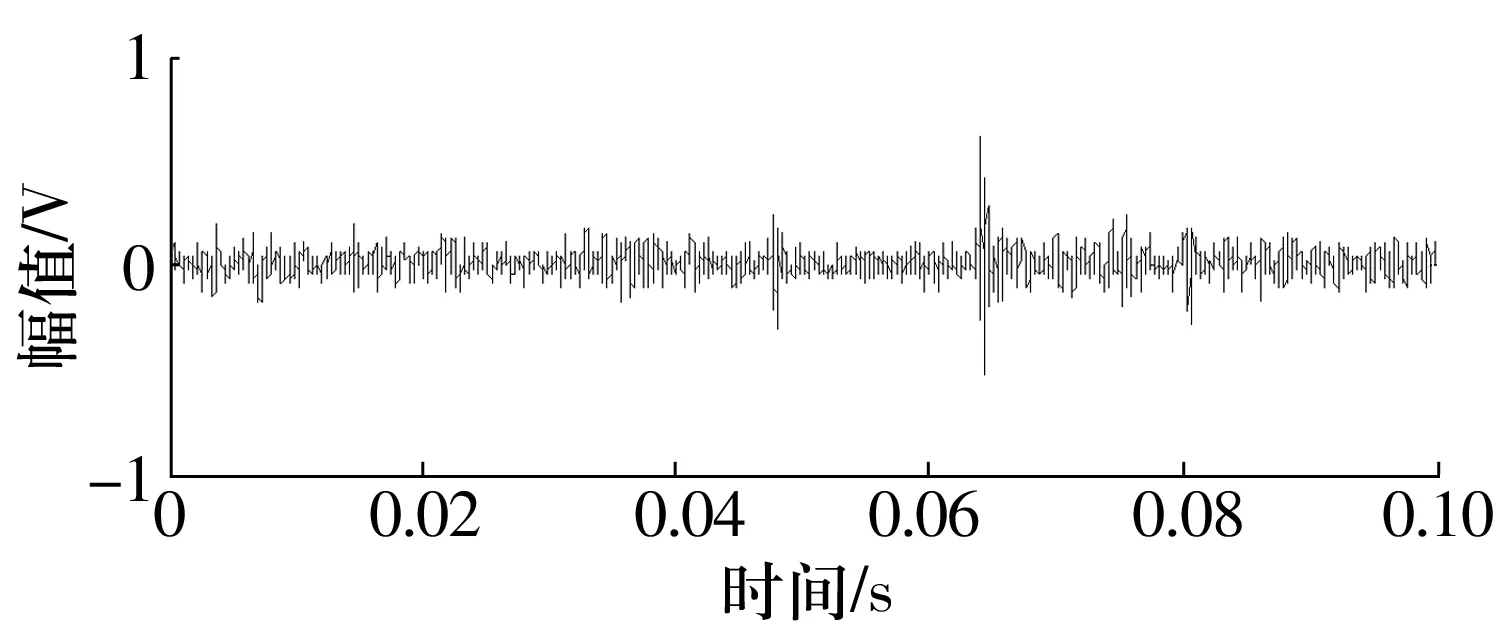
图4 外圈故障信号Fig.4 Fault signal in outer ring

图5 外圈故障信号稀疏系数及其包络谱Fig.5 Sparse coefficient and its envelope spectrum of fault signal in outer ring

从图5可以看出，稀疏系数集中于故障信号中的4个主要冲击成分位置，可从其包络谱中提取出61.04 Hz的故障特征频率，与外圈故障特征频率理论值59.76 Hz相近。

3.2 内圈故障特征提取

同样截取一段内圈故障信号进行分析，参数设定与外圈信号分析一致，结果如图6所示。从图中可以看出，通过改进算法处理后提取出的故障特征频率为100.7 Hz，与内圈故障特征频率理论值100.97 Hz相近。虽然内圈故障特征成分受采集传递路径等因素影响在信号中表现较微弱，但处理结果表明改进算法同样适用于内圈故障特征提取。

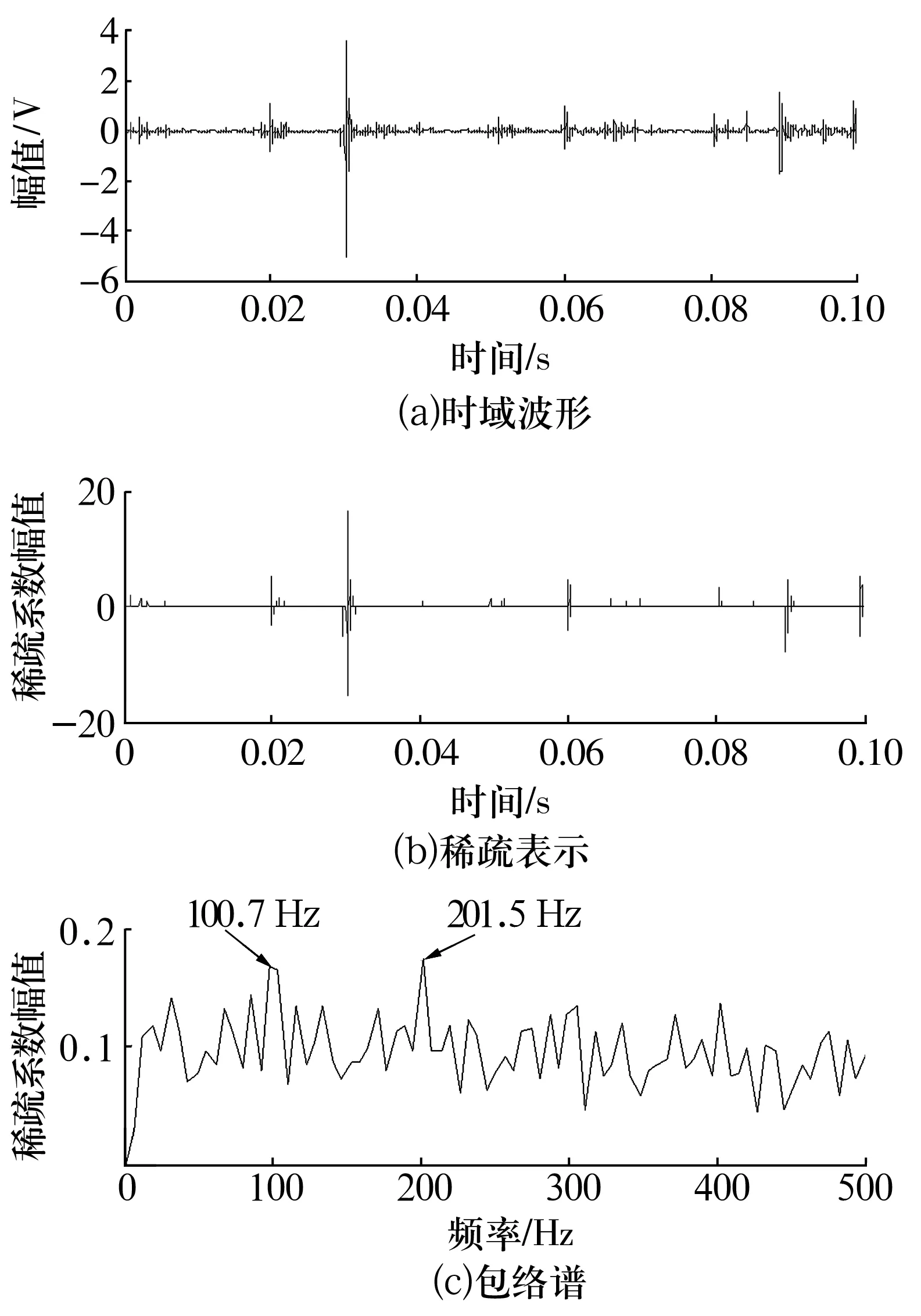
图6 内圈故障信号处理Fig.6 Processing of fault signal in inner ring

3.3 处理效率对比

对比现有的基于Laplace小波构造的过完备字典稀疏表示方法，参数设定一致，内、外圈故障信号的处理时间见表1。由表可知，稀疏表示结果相似的情况下，改进算法所需时间明显缩短，效率更高。

表1 算法运算效率比较Tab.1 Comparison of computation efficiency of algorithm

4 结束语

针对滚动轴承故障信号的稀疏表示问题，提出一种基于改进Laplace小波字典的滚动轴承故障诊断新方法，通过优化方法提高计算效率，并实现滚动轴承故障冲击信号的稀疏表示；通过对稀疏系数进一步的频谱分析，可以有效判断滚动轴承的故障类型。

但是，如果在计算过程中信号维度过大，依然会造成字典过大的问题，导致计算失败。因此可针对这一问题，进一步开展信号降维方法及字典结构优化方法的研究。