基于分析矩阵零均值比的CDL卷积交织盲识别

龙 浪, 杨俊安, 刘 辉, 梁宗伟

(1. 国防科技大学电子对抗学院, 安徽 合肥 230037; 2. 安徽省电子制约技术重点实验室, 安徽 合肥 230037)

0 引 言

在现在及未来的高科技信息战、电子战中,通用数据链(common data link,CDL)系统具有极其重要的地位,外军尤其是美国军方对其十分重视,是美国和北约指定的传送图像和信号情报的标准数据链,在近几次局部战争中都发挥了十分重要的作用[1-2],对CDL的对抗研究已成为通信对抗的一个重要研究方向。

CDL系统中,通常采用卷积交织技术来对突发或序列差错进行补偿,增强了信道编码技术的纠错能力,但同时也大大增加了侦察难度,并且受到高传输速率和深衰落信道的影响,导致非合作侦察数据的误码率会有一定的提升[3],这给实现数据链信号的卷积交织盲识别带来了极大的困难。

近年来,国内外对卷积交织参数盲识别的研究,已取得一系列研究成果。但针对CDL这类基于RS(Reed-Solomon)码传输的高速数据系统的交织参数盲识别方法,尚未有公开发表的文献。现有的卷积交织盲识别方法主要包括多重循环搜索方法[4]和基于秩准则算法[5-8]。但这两种方法,都必须是在分组码长恰好等于交织深度与交织宽度的乘积时,才能实现参数的盲识别。在非合作通信中,由于缺少先验信息,方法具有较大局限性,限制了在实际操作中的应用,并且这两种方法的抗误码性能较差,不适用于CDL高误码卷积交织模型。

本文针对现有盲识别方法存在码长约束且抗误码性能较差的问题,提出了一种基于分析矩阵零均值比的CDL卷积交织参数盲识别方法,在不需要考虑码长约束的情况下,建立了分析矩阵,通过高斯约当(Gauss-Jordan elimination through pivoting,GJETP)算法获得分析矩阵的零均值比,从而得到秩缺间隔,最后通过联合求取交织宽度、交织深度和交织偏差实现了CDL中卷积交织参数的盲识别,并对本文算法、多重循环搜索算法和秩准则算法在不同误码性能下进行了仿真实验。

1 基本原理

1.1 CDL中的卷积交织模型

为获得更强的纠错能力、相对小的译码复杂度[9],在CDL前向链路中通常采用RS码[10-12]和卷积码[13-15]的级联编码[16-18]来提高传输的可靠性,仿真模型如图1所示。该模型包括RS编码、卷积交织和卷积编码。在CDL系统中,由于高传输速率和深衰落信道的影响,卷积码译码不能有效地纠正突发错误,采用卷积交织技术[19-21]能够对码流进行扰乱,通过解交织后,突发错误就转换为随机错误,有利于在RS解码时能够更有效地进行纠错。

图1 CDL级联码的工作原理Fig.1 Operating principle of concatenated code for CDL

在CDL系统中,卷积交织器(B,M)的工作结构如图2所示,其中,B为交织深度即支路数；M为交织宽度即延迟数,在第i条支路上有(i-1)M个延迟单元。原始信息数据流分为B个一组,在转换开关的作用下依次进入B条支路,周而复始;输出端也同样在转换开关的作用下从B条支路取出数据,交织和解交织都是同步进行的。

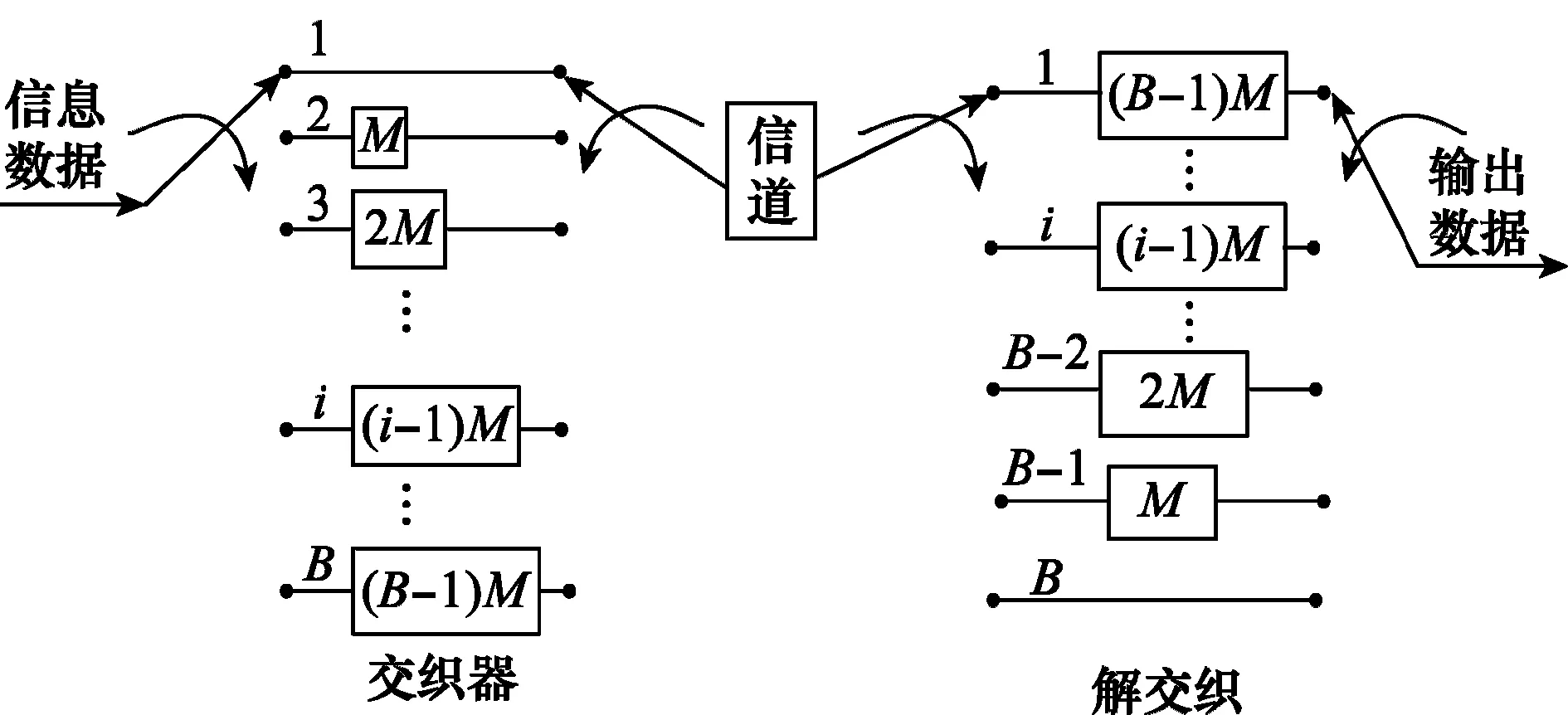
图2 卷积交织和解交织的结构Fig.2 Structure of convolutional interleaver and de-interleaver

1.2 GJETP算法

在求解线性方程组时,经常会利用GJETP算法计算系数矩阵的秩,通过对其进行初等变换,将其化成一个下三角矩阵,其算法的实现步骤如下[22]。

令A为系数矩阵,是m×n阶矩阵,E1,E2分别是n阶、m阶的单位方阵。令i从1到n循环,步长为1,每次循环进行以下步骤:

步骤1若A(i,i)=0,则交换A(:,i)与A(:,i′),其中,A(:,i′)=1,且A(:,i′)为A(i,:)的首一非0元素(i′>i),并交换E1(:,i)与E1(:,i′);

步骤2若A(i,i)=0,即A在步骤1中未进行列交换,则交换A(i,:)与A(i′,:),其中,A(i′,i)=1,且A(i′,i)为A(:,i)的首一非0元素(i′>i),并交换E2(i,:)与E2(i′,:);

步骤3若A(i,i)=1,则A(:,i′)=A(:,i)⊕A(:,i′),其中,A(i,i′)为A(i,:)的所有非0元素(i′>i),并令E1(:,i′)=E1(:,i)⊕E1(:,i′);

当上述所有循环结束后,所得的矩阵即为所需的下三角矩阵。

2 新的卷积交织盲识别算法

CDL系统中,RS码是以二进制码流进行传输的,在对CDL数据链进行侦察时,获得的(nc,k,m)RS码序列为伽罗华域(Galois felid,GF)GF(2m)码元在GF(2)上映射得到的二进制(mnc,mk)线性分组码[23-25],其中,nc为码长;k为信息长度;m为码字宽度,因而可利用基于线性分组码的卷积交织盲识别方法来实现基于RS码的卷积交织参数盲识别。

2.1 分析矩阵模型

将截获到的数据流经过解调、解卷积等预处理后,按行放入一个r×b的矩阵A中,其中,r表示矩阵的行数;b表示矩阵的列数,可取b1,b2,…,bn,则此时对应的分析矩阵为A1,A2,…,An,但必须要满足r≫b。如果每行中含有t组完整码字,且对齐正确,如图3(a)所示,则根据线性分组码的特点:在一个码字内信息码元相互统计独立,校验码元与信息码元线性相关,当对矩阵A进行列变换后,分析矩阵将会出现秩的缺失;反之,若没有对齐,如图3(b)所示,则分析矩阵为满秩矩阵[26]。

图3 秩缺与满秩Fig.3 Deficient rank and full rank

2.2 卷积交织盲识别原理

传统方法在对卷积交织参数盲识别时,要求交织深度与码长必须为倍数关系,不具有一般性和实用性。在本文提出的算法中,则不需要考虑这种倍数关系,只要当分析矩阵的列数b满足式(1)时,分析矩阵中各行的码字就能保持对齐,此时再利用GJETP算法对矩阵A进行列变换后,由于校验码元与信息码元之间的线性相关性,分析矩阵就会出现秩缺失的情况。

b=κlcm(mnc,B)=αmnc

(1)

式中,κ,α为正整数(κ,α=1,2,3…);lcm(mnc,B)表示mnc与B的最小公倍数。

根据卷积交织的原理和性质可知,此时矩阵A中,每行至少含有λ(λ<α)个完整的码字,通过计算可得矩阵的秩为

rank(A)=λmk+(mnc(α-λ))=λmk+b-λmnc

(2)

其余情况下,变换后的分析矩阵均为满秩。

因此,在利用GJETP算法对矩阵A进行处理后,可以通过观察相继出现秩缺失的分析矩阵列数的差值来获得秩缺间隔γ，即

γ=lcm(mnc,B)

(3)

在无噪环境下,可利用直接对矩阵A求秩来获得γ,然而在实际的传输中,受环境噪声的影响,传输数据存在错误比特数,此时分析矩阵可能不会出现秩缺失的情况。

在传统方法中,通常选择使用列的汉明重量与门限值的比较来判断是否出现秩缺失,然而由于人为选择的门限缺乏准确性,导致在噪声环境下,传统方法的识别性能较差,因此,本文引入零均值比这个概念来削弱噪声的影响。

在有噪的情况下,利用GJETP算法将矩阵A转换成为三角矩阵Q,通过对下三角阵Q的观察发现,存在秩缺失的矩阵比满秩矩阵含有更多的“0”,故定义零均值比u(b)来表示矩阵的秩缺失情况,表示为

(4)

式中,φ(c)表示下三角矩阵Q中第c列含“0”数目所占比重,表示为

(5)

式中,φ(c)表示第c列中“0”的数目。

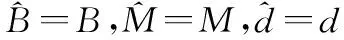
2.3 算法流程

步骤1将截获到的数据先进行解调,解卷积等预处理后,按行放入r×b的矩阵A,其中b∈[bmin,bmax]且满足r≫b。

步骤2在无噪情况下直接求秩,记录连续秩缺失的列数差值,即为γ;在有噪环境下,利用GJETP算法将矩阵A转换为下三角矩阵Q,并计算出u(b),记录连续u(b)较大值的列数差值,即为γ。

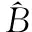
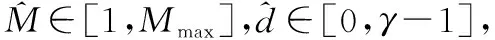
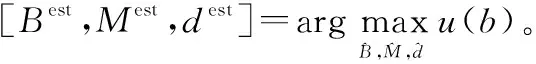
3 实验仿真与性能分析

3.1 实验仿真与结果

为了验证本文算法性能,按照美军CDL标准[27]仿真了CDL数据,仿真参数设置如下:采用二进制相移键控(binary phase shift keying，BPSK)扩频调制,数据传输速率为200 kb/s,(8,6,4)RS编码,(2,1,7)卷积编码,在假设交织延时偏差d为0的情况下,分别取交织深度B和交织宽度M的组合为(4,8)和(3,16)这两种情况,在无噪和信噪比(signal-to-noise ratio,SNR)为10 dB,误码率(bit error ratio,BER)为0.02的有噪环境下进行仿真实验。

在无噪情况下,如图4所示,两种交织参数设置下的秩缺间隔分别为32和96,与理论结果保持一致,验证了该方法的可行性。

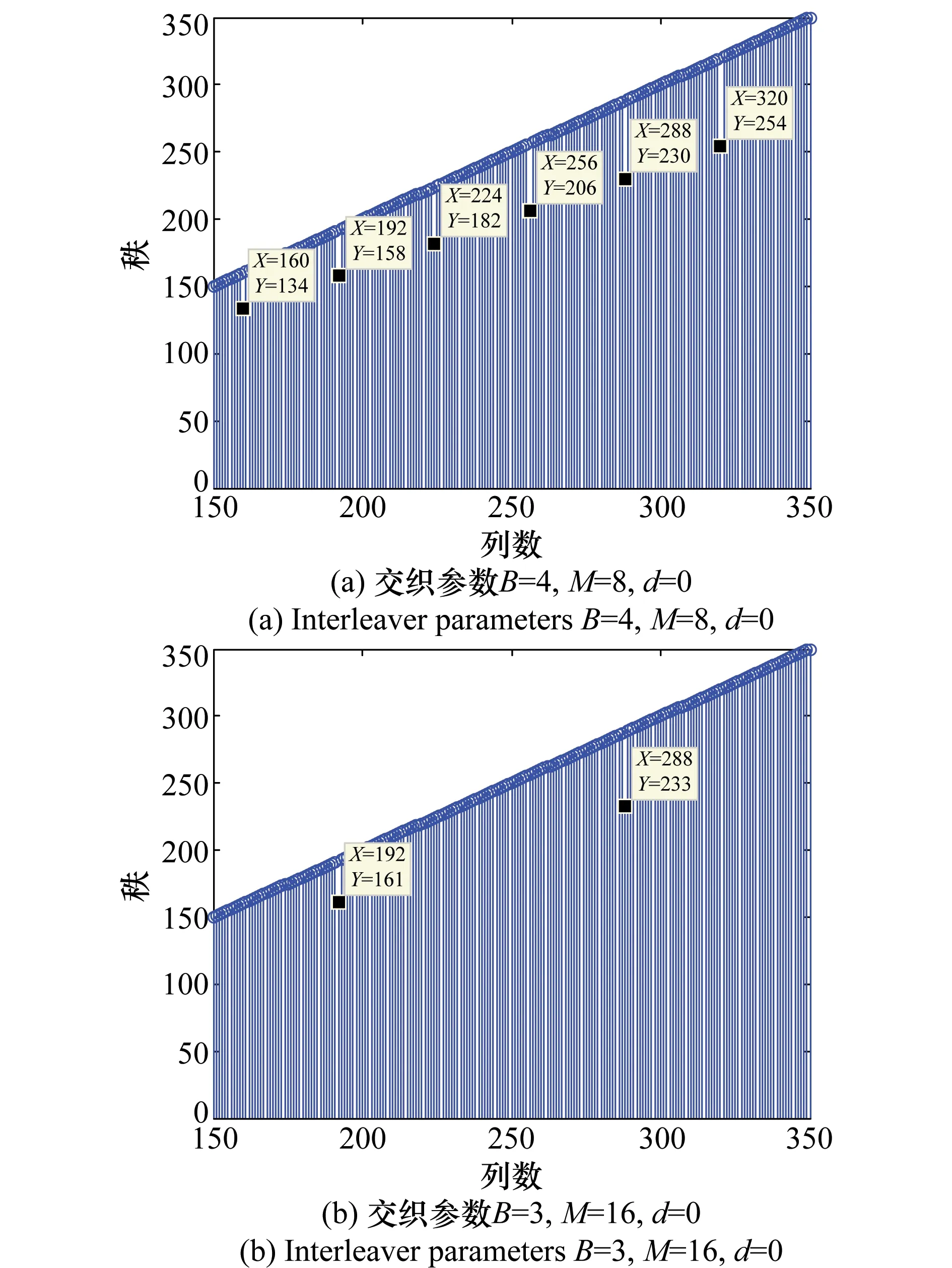
图4 无噪情况下不同交织参数分析矩阵的秩Fig.4 Rank of different interleaver parameters for noiseless scenario

在有噪情况下,分析矩阵的零均值比随分析矩阵的列数变化情况如图5所示,从图5中可以看出,此时零均值比的相邻峰值间隔分别为32和96,与在无噪下的秩缺间隔保持一致,验证了基于零均值比的盲识别算法具有较好的抗噪性能。

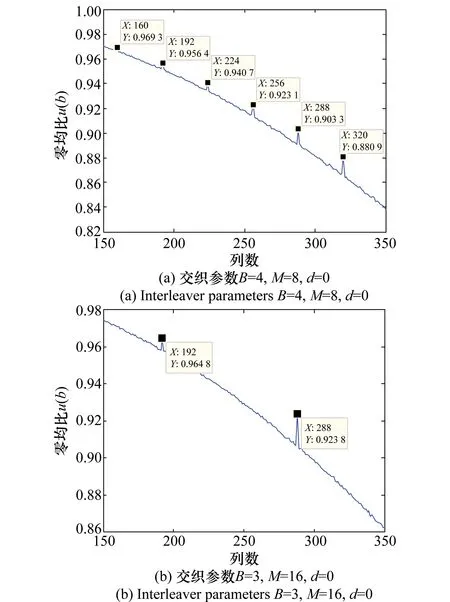
图5 有噪情况下不同交织参数分析矩阵的零均值比Fig.5 Zero-mean-ratio of different interleaver parameters for noisy scenario

在得到秩缺间隔后,由式(3)可得秩缺间隔与码长及交织深度的关系,由于码长未知性,考虑对所有满足条件的交织深度B进行求取,并利用所有可能的参数组合对其进行解交织,得到解交织后的数据的分析矩阵,其对应的零均值比如图6所示,从图6中可以看出,当交织参数与实际参数一致时,u(b)达到最大值,此时即完成了对卷积交织参数的识别。

3.2 性能对比分析

为了验证本文算法的性能。分别对算法在不同m值,不同矩阵行数值,不同BER的条件下进行了估计精度性能分析,并选择在交织参数[B,M,d]为[4, 8, 0]时,对多重循环搜索算法[4]、秩准则算法[7]和本文算法进行蒙特卡罗仿真,比较在不同误码下的识别性能,仿真结果如图7和图8所示。

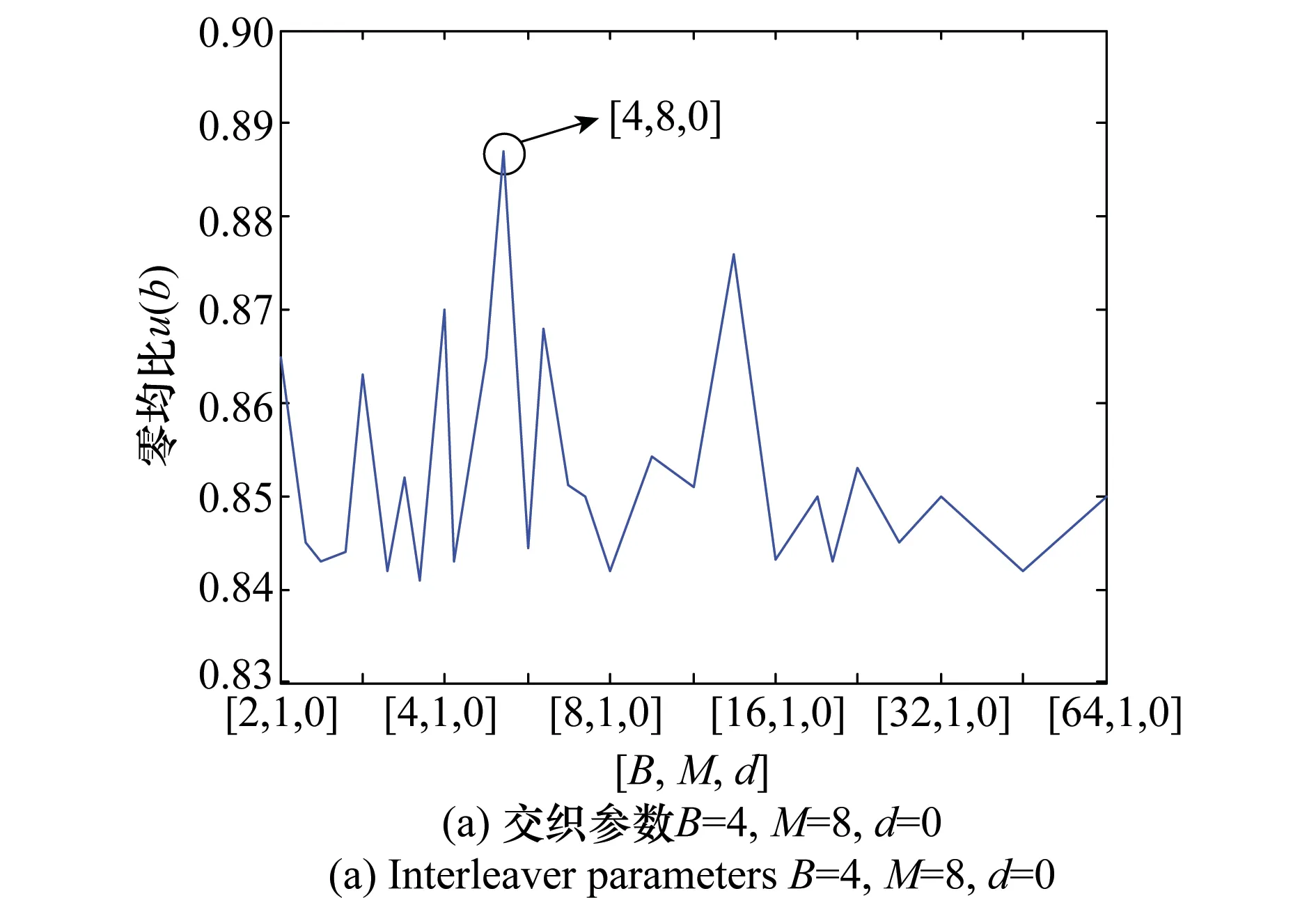
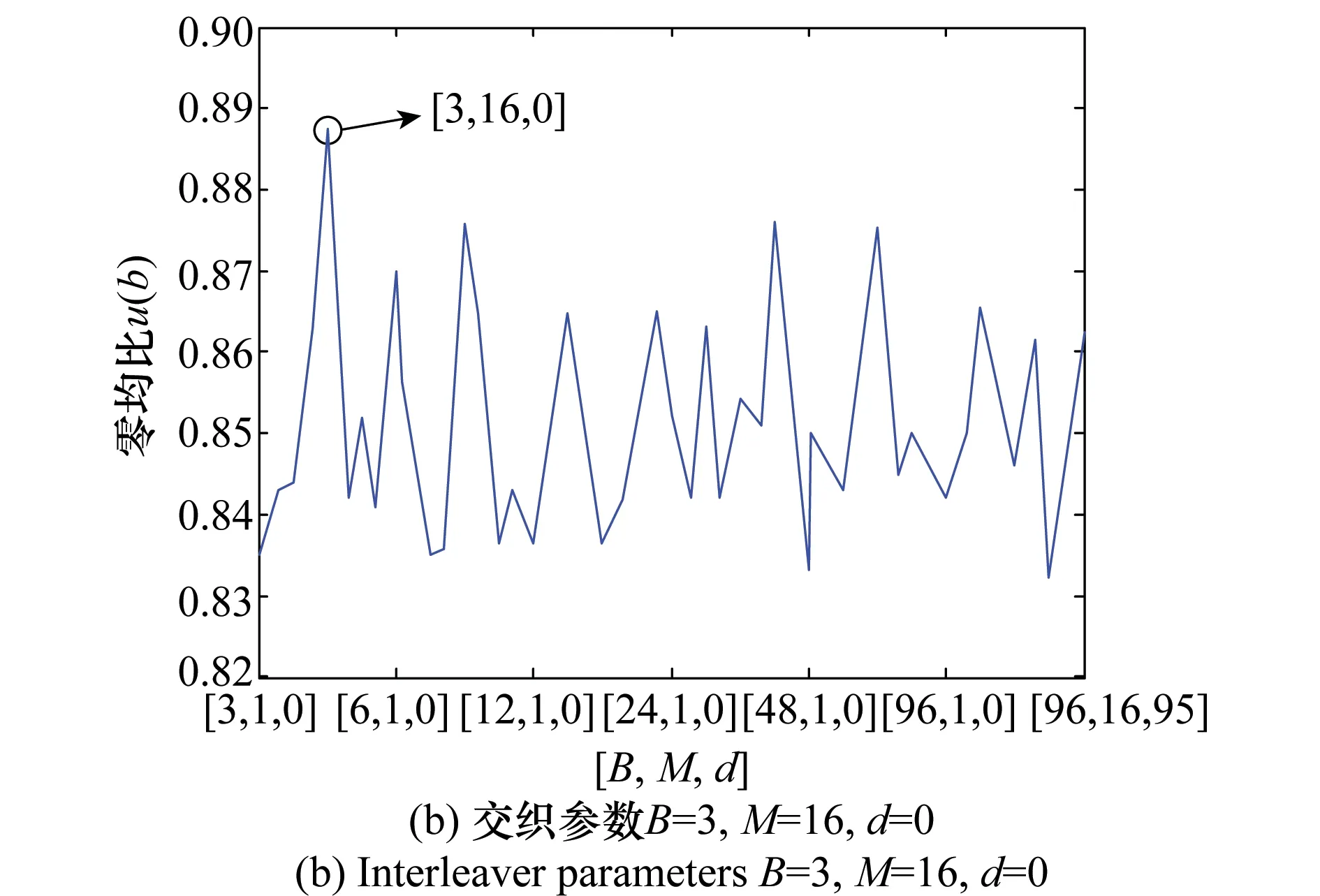
图6 有噪情况下不同解交织后的零均值比Fig.6 Zero-mean-ratio after de-interleaver using all possible combination of for noisy scenario

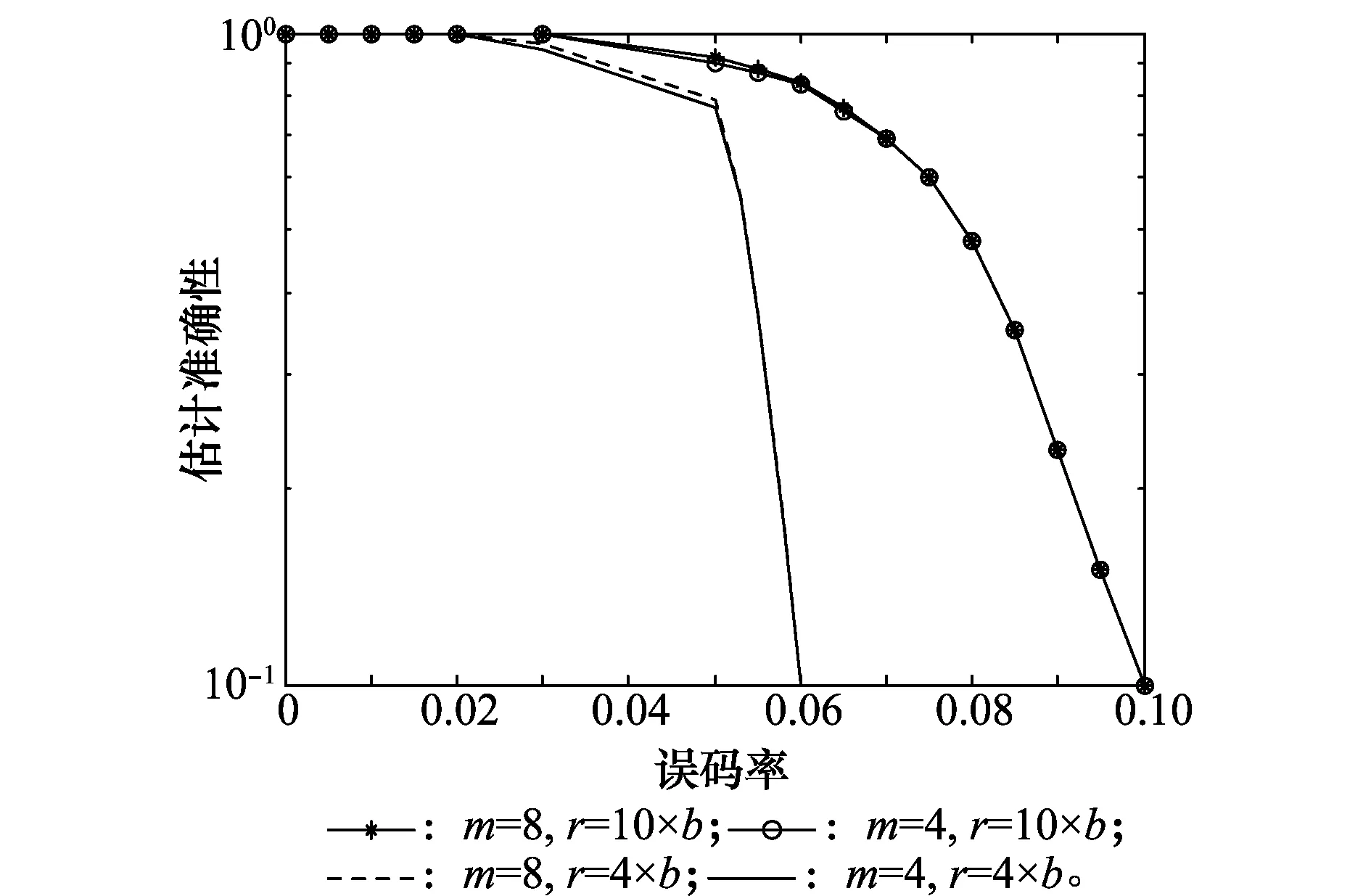
图7 不同参数下算法识别性能的比较Fig.7 Comparison of recognition performance among different parameters

图8 3种算法识别性能比较Fig.8 Comparison of recognition performance among different three algorithms

从图7中的结果可知,卷积交织参数的估计准确性,随着m的增大,基本保持不变,但随着r的增大,估计准确性具有较大的提高。由于m增大时,矩阵秩不会发生明显改变,在有噪信道下u(b)值也基本保持不变,不能提高γ的估计精度,故估计准确性不受m的影响。但随着行数的增加,γ这一重要参数的估计也更加准确,因此,在有噪信道中,估计精度将会随着分析矩阵的增大而提高。

从图8中可以看出,随着误码率的增加,3种算法的性能都有一定程度的下降,但本文算法的下降速度相对较慢。当系统BER超过0.03时,两种传统的方法已无法正确估计出参数,但本文算法仍能较好地估计出卷积交织参数,表明本文算法具有良好的抗误码性能。

3.3 运算复杂度分析

4 结 论

本文针对RS码提出了一种适用于CDL高速传输下基于分析矩阵零均值比的卷积交织盲识别方法,通过GJETP算法获得的分析矩阵零均值比,从而得到秩缺间隔,最后通过联合求取交织深度、交织宽度和交织偏差来完成卷积交织参数的盲识别。仿真实验结果表明,利用本文方法在对截获数据的交织参数盲识别中,不受码长与交织参数之间的限制,更具有普遍性,且相比于多重循环算法和秩准则算法具有更好的抗误码性能,运算量也相对较小,能够比较好地完成CDL系统中的卷积交织参数盲识别。