基于旋转干涉仪的多目标参数估计
申皓明, 廖桂生, 杨志伟
(西安电子科技大学雷达信号处理国家重点实验室, 陕西 西安 710071)
0 引 言
随着需求的增长以及科技的发展,电子侦察卫星已经成为获取各种情报的重要手段,在现代战争中有着无可替代的地位[1]。目标定位是电子侦察卫星的一项重要应用,其获得的目标位置是侦察信息中最为重要的信息之一。而如何获得高精度的多目标定位结果是提高定位系统性能的关键问题。
对于传统的处理方式:①单星测角定位,其优点是系统易于实现,但由于天线孔径和载荷的限制,测向精度不高[2-4],在文献[5] 提出了一种基于粒子群算法的无源定位技术,有相对较好的结果,但是计算复杂度较高,文献[6]提出了基于脉冲信号到达时间的单卫星无源定位方法,利用网格搜索的方法对辐射源的位置进行估计,系统的定位精度较低,且需要长时间观测,对高速运动目标定位精度较差,无法对短时目标进行定位。②相位干涉仪测向系统具有测向精度高、系统实现复杂度低、计算复杂度低、可实时处理等优势,但该方法随着测角精度的不断提高会造成角度模糊范围的不断扩大[7-12],即干涉仪系统的基线越长,测向结果越精确,同时产生的角度模糊越严重,无法得到真实目标的角度信息。而基于旋转干涉仪的测向解模糊算法能有效解决测角精度与角度模糊范围的矛盾问题[13-18],利用基线旋转不同的角度并测量相位差进行角度估计,但这类方法只对单目标情况,在多目标情况下,算法失效。③传统的阵列信号处理方式可以解决多个目标角度估计的问题,但为避免角度模糊的影响,阵元间距不超过半波长。星载阵列为得到较高的角度分辨率对孔径要求比较大,系统的实现要由很多的阵元组成。由于载荷限制,星载阵列阵元数目较少,阵列的孔径太小,定位系统的性能受到很大的限制。④文献[19]提出了一种基于旋转干涉仪的多目标角度估计方法,可以对工作时长不同的同频目标源信号进行检测,通过各目标源在时间上的差异完成多目标角度的估计,但对于同频同时工作的信号源无法进行分辨。
针对以上问题,本文提出了一种将多重信号分类(multiple signal classification, MUSIC)算法和霍夫变换[20-27]思想相结合的多目标参数估计算法。该方法可以在较大的阵元间距下,通过对角度模糊信息的提取,实现在较大的孔径下利用少量阵元对多个目标进行角度估计。首先利用不同时刻的采样数据通过MUSIC算法对信号进行一维谱估计,再将估计值按时间排列,不同目标的角度模糊随时间按照一定的反三角函数曲线规律变化,接着通过霍夫变换的思想在二维角度参数空间中对特定曲线进行参数提取,实现多目标的二维角度估计。
1 系统模型建立
1.1 旋转干涉仪模型
图1为旋转干涉仪模型,图1中干涉仪以第一个阵元为参考阵元建立空间三维直角坐标系,两个阵元间距为d,其中d≫λ/2。设阵列天线在xOy平面内绕第一个阵元沿逆时针方向以角速度ω做匀速圆周运动。假设信号为远场窄带信号,以x轴与y轴为参考, 辐射源相对于坐标系的俯仰角为β,其中,俯仰角的范围为[0,π/2) ,表示和z轴正方向的夹角;方位角为α,其中,方位角的取值范围为[0,2π),表示和x轴正方向的夹角(逆时针方向旋转)。在基线旋转过程中,两天线间的相位差随基线与辐射源夹角的变化而变化。
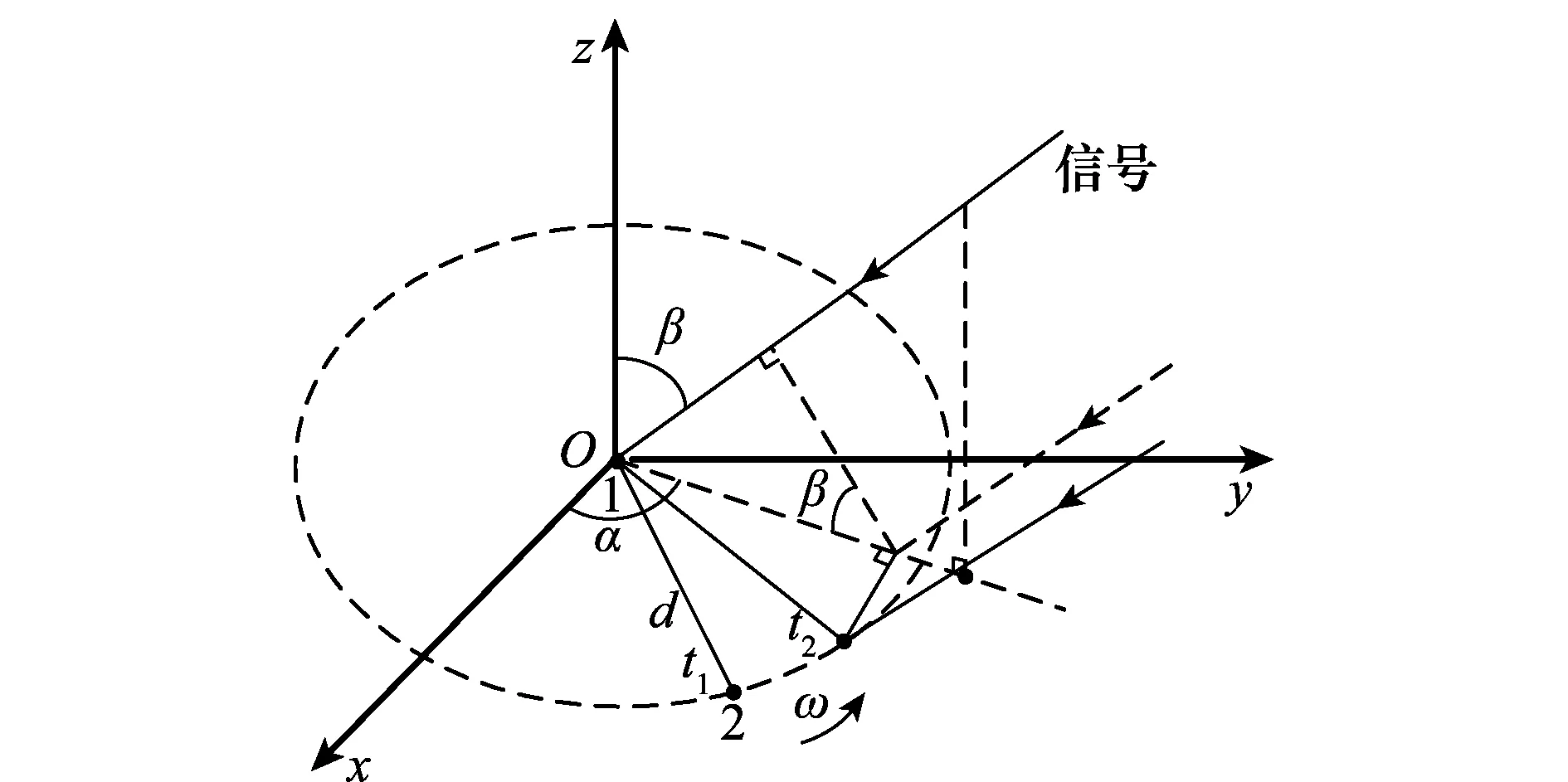
图1 旋转干涉仪模型Fig.1 Rotating interferometer model
由图1可知,相对与参考阵元,阵元接收到信号为
x(t)=s(t)ejφ(t)+σn
(1)
式中,s(t)表示信号源的包络;σn为阵元1上的高斯白噪声,服从正态分布N(0,σ2);φ(t)表示在t时刻阵元2与阵元1之间的相位差。两个天线单元间接收到信号的相位差为
(2)
式中,λ为辐射源波长;β,α分别为信源的入射俯仰角和方位角;d为干涉仪阵元间的间距,其中间距d≫λ/2。由式(9)可以看出,当俯仰角β固定不变时,相位差受天线基线旋转的影响呈余弦规律变化。
1.2 多通道旋转干涉仪模型
图2为多通道旋转干涉仪模型,图2中干涉仪变为多个接收通道,阵元间距为d。设阵列天线在xOy平面内绕第一个阵元沿逆时针方向以角速度ω做匀速圆周运动。
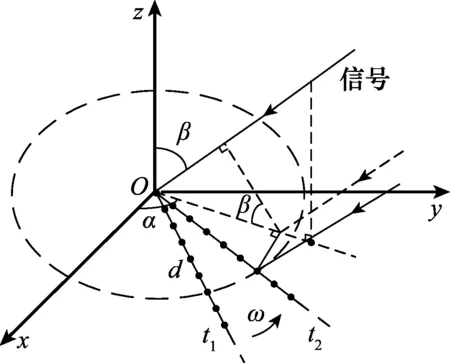
图2 多通道旋转干涉仪模型Fig.2 Multichannel rotating interferometer model
由图2可知,相对与参考阵元,剩余天线单元接收到信号为
xi(t)=s(t)ejφi(t)+σn
(3)
式中,s(t)表示信号源的包络;σn为阵元的高斯白噪声,服从正态分布N(0,σ2);φi(t)为t时刻阵元i与第一个阵元间的相位差。两天线接收到信号的相位差为
(4)
假设旋转干涉仪有N个阵元,空间中有L个信号,其中信号的方位角,俯仰角分别为α1,α2,…,αL,β1,β2,…,βL,可以得到干涉仪阵元间相位差矩阵为
Φ(t)=[Φα1,β1(t),Φα2,β2(t),…,ΦαL,βL(t)]
(5)
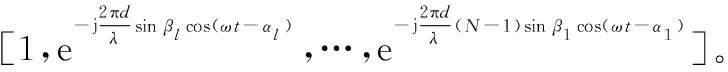
(6)
将式(6)化简为
X(t)=Φ(t)S(t)+N(t)
(7)
式中,X(t)为阵列采样得到的接收数据;Φ(t)为N×L维阵元间相位差变化矩阵;S(t)表示空间信号;N(t)表示噪声矩阵。
1.3 目标角度模糊分布模型
根据第1.2节所述模型,多通道旋转干涉仪天线阵元数目为N,信源个数为L,信号俯仰角为β,方位角为α,阵元间距为d≫λ/2,在阵列信号处理中会出现角度模糊,假设d=m(λ/2),则两个阵元间相位差为
mπsinβcos(ωt-α)
(8)
由式(4)可知,距旋转线阵的阵列流型阵随时间呈余弦变化,因为卫星天线旋转的角速度ω远大于采样周期Ts,所以利用MUSIC算法对目标角度估计时,在快拍积累时间内认为阵流型是不变的。
在ti时刻对目标的俯仰角进行一维的谱峰搜索,搜索导向矢量只考虑俯仰角的变化,即
(9)
对exp(-j2πdsinβcos(ωti-α)/λ),其中sinβcos(ωti-α)的取值范围为(-1,1),所以θ∈(-90°,90°)。谱峰搜索变为求解式(10)。
(10)
将d=m(λ/2)代入得
(11)
exp(-jmπsinβcos(ωti-α))
(12)
在对谱峰搜索的过程中,θ∈(-90°,90°),则
(13)
式中,(πsinθ±2kπ)∈[-mπ,mπ],即k∈[(-m-sinθ)/2,(m-sinθ)/2]。代入式(7)得
exp(-j(πsinθ±2kπ))=exp(-jmπsinβcos(ωti-α))
(14)
化简得
(15)
最终得到的一维谱估计值为
(16)
式中,θ(ti,k)表示在ti时刻谱峰搜索中搜索到的第k个峰值;ω为天线旋转角速度;2k/m为曲线基线位置,式(16)说明在一次MUSIC角度估计中,由于阵元间距d=m(λ/2)≫2/λ,谱峰搜索过程中会出现多个峰值,其中,由式(13)可知,峰值个数M=2d/λ=m,图3为当d=8(λ/2),信号源数目为2时,利用MUSIC算法进行俯仰维的一维谱峰搜索。
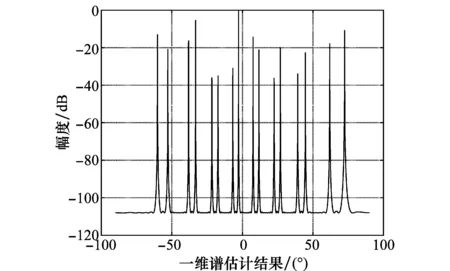
图3 MUSIC方法角度估计结果Fig.3 Angle estimation results by MUSIC method
整个天线旋转过程,谱峰随时间的分布为
(17)
由式(17)可知,峰值位置随时间变化关系为反三角函数与三角函数构成的复合函数。由于θ(t,0)是非线性函数,简便运算复杂度,只分析k=0的情况。在θ(t,0)中,当k=0时,θ(t,0)∈[-β,+β],所以β为θ(t,0)曲线的幅度,α为曲线的初相。如图4所示,信号源数目为2,阵元间距分别为d=λ/2和d=8(λ/2),将天线旋转一个周期内多次估计的谱峰值提取出,按时间排列在一起。
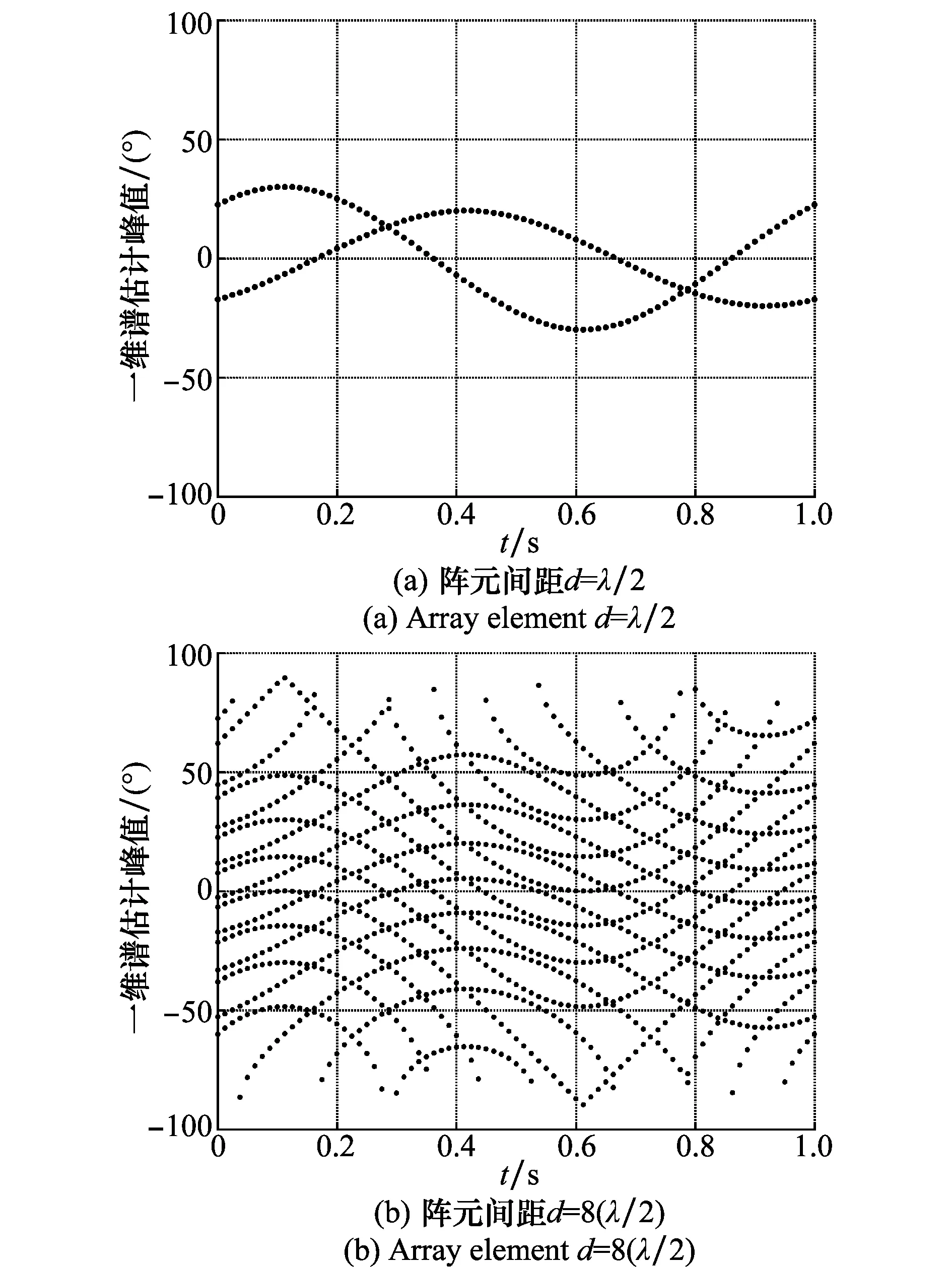
图4 天线旋转一周的MUSIC估计Fig.4 MUSIC estimation of antenna rotation with one cycle
在图4(a)中,阵元间距为半波长,测向过程中不会产生角度模糊,此时曲线的k=0,即角度曲线的基线为零,图4(a)中两条曲线分别对应相应的两个信号源,其中每条曲线的幅度和初相均为相应信号源的俯仰角β,方位角α。在图4(b),阵元间距d=8(λ/2),故在除了基线位置为零的曲线外,仍出现多条反三角函数曲线,图4(b)中这些基线不为零的曲线均为测向过程中角度模糊对应的峰值曲线,因为在单次谱峰搜索过程中无法区分所得谱峰是真实值还是模糊值,因此真实值不能单独提取出,只能将模糊值与真实值全部列出。综上只需要对所有基线位置为零的曲线进行参数估计,得到相应曲线的幅度和相位信息,即可完成所有信号源的俯仰角β、方位角α的估计,实现多目标角度解模糊。
2 本文算法原理
提取的峰值曲线表达式为
(18)
在参数估计中,化简参数积累过程,只需考虑2k/m=0的情况。则式(18)变为
θ(t)=arcsin(sinβcos(ωt-α))
(19)
式中,因为天线旋转角速度ω已知,在曲线参数估计中只需对俯仰角β、方位角α进行估计。
下面对峰值曲线的Hough变换原理作以说明。式(19)中β,α为常数,分别代表曲线的幅度和初相。对曲线上任意一点(ti,θ(ti))来说,在θ(t)-t构成的二维平面中有无数条曲线可以通过该点。若将θ(ti),ti视为常数,β,α视为变量,其中β∈(0~90°),α∈(0~360°),则式(19)变为
(20)
通过式(19)的变换,将峰值曲线上的点(ti,θ(ti))变换为α-β的二维参数空间中的一条曲线,即完成对(ti,θ(ti))点的Hough变换。Hough变换原理如图5所示,图5中θ(t)-t的二维坐标系中峰值曲线为θ(t)=arcsin(sinβ1cos(ωt-α1)),在峰值曲线中任取3个点:(t1,θ(t1))、(t2,θ(t2))和(t3,θ(t3)),将这3个点分别代入式(20)中,可得到参数空间中对应的曲线,3条曲线有共同的交点(α1,β1)。因此将峰值曲线上所有点都投影到参数空间,每个点在参数空间都有对应的曲线,这些曲线在参数空间有共同的交点(α1,β1),对参数空间中曲线上每个点的出现次数进行统计,统计次数最多的点对应的坐标位置便是峰值曲线的参数。
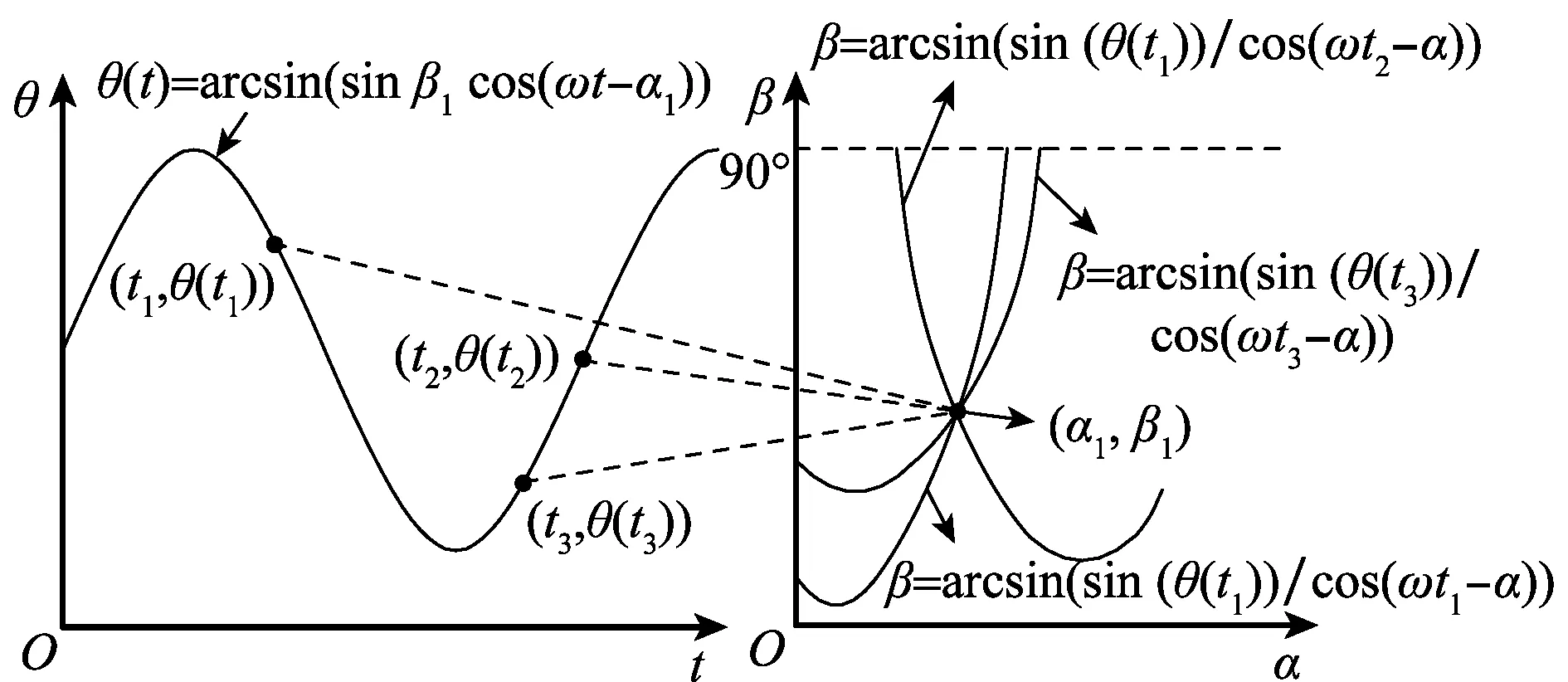
图5 Hough变换原理Fig.5 Hough transform principle
假设空间中L个信号源的峰值曲线向参数空间投影:①凡是k/m=0的峰值曲线在向式(17)构造的参数空间投影后都可以在相应参数点(αl,βl)处积累出一个极大值,其中,l=1,2,…,L,由此实现多目标的检测;②各极大值点的坐标(αl,βl)分别为各峰值曲线的初相和幅度,即对应各信号源的方位角和俯仰角,对于一个信号源而言,得到一个极大值点的坐标即可同时得到方位角和俯仰角的估计,避免了信号源间的参数配对问题;③对于k/m≠0的曲线向式(17)构造的参数空间中投影没有固定的交点,所以角度模糊产生的峰值曲线在参数空间中无法得到有效积累,由此避免了角度模糊影响,实现目标的解模糊。图6给出了多目标情况下的Hough变换示意图。
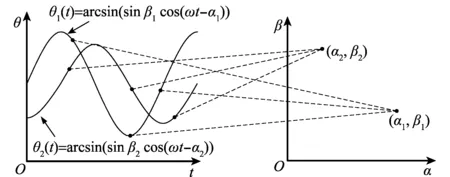
图6 多曲线Hough变换示意图Fig.6 Schematic diagram of multiple curve Hough transform
本文算法具体检测方案流程如图7所示。

图7 数据处理流程图Fig.7 Data processing flow chart
算法步骤如下:
步骤1设参数空间中的角度精度为P,参数空间累加矩阵CA[β][α],维数为(90/P)×(360/P),初始时刻所有元素置零。
步骤2令方位角α从0到360°以角度精度P变化,利用峰值点θ(t)和对应时刻t代入式(17)计算不同α取值下俯仰角β的值:
步骤3若β在(0~90°)范围以内,则在CA[α/P][β/P]位置处累加1。若β不在(0~90°)范围以内,则舍弃该次计算结果。直到干涉仪旋转过程中所有峰值点都被计算过。
步骤4对CA[β][α]矩阵进行遍历,搜索得到最大的L个峰值,每个峰值的坐标位置代表该目标的方位角,俯仰角信息。第l个峰值的所处位置的值分别该目标的方位角αl,俯仰角βl。完成多信号源的二维角度解模糊,实现目标定位。
算法流程图如图8所示。
算法复杂度分析,在算法计算过程中,P为角度搜索精度,L为信号源个数,m为阵列天线的阵元间距对半波长的倍数,设天线旋转过程中角度估计频率为fE,天线旋转时间为t,在系统结构确定时,L,m,fE,P这4个参数为常数,则算法计算复杂度为O(LmfE/P·t),即复杂度是O(t),为线性阶复杂度。算法复杂度较低,天线旋转过程中,在每完成一次一维角度估计后即可将结果向参数空间投影做参数积累。
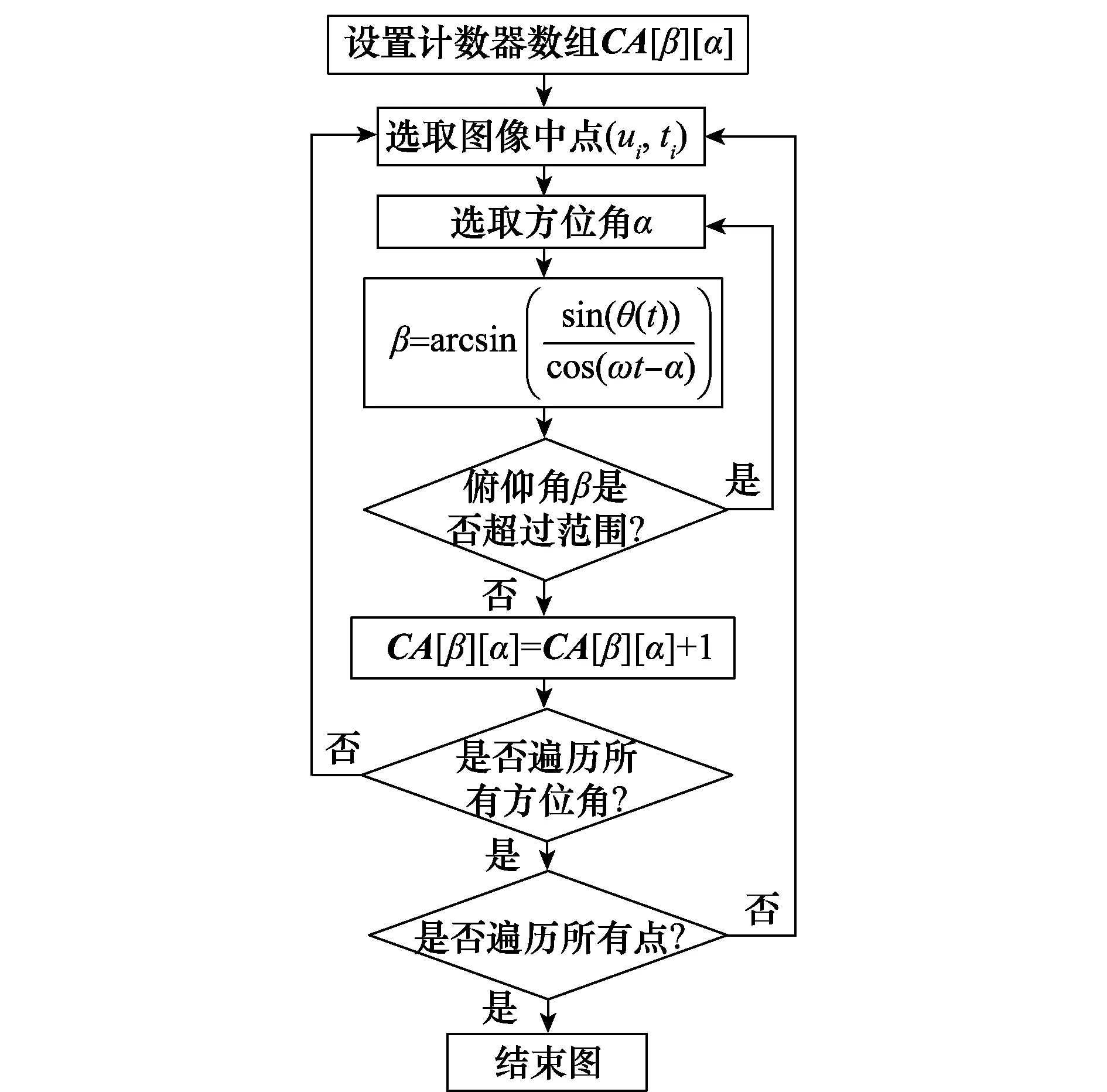
图8 算法流程图Fig.8 Algorithm flow chart
3 仿真实验与分析
本小节在零均值高斯白噪声背景下进行,通过不同目标二维角度估计仿真实验来验证本文方法对多目标角度解模糊的有效性。
3.1 曲线参数检测算法有效性仿真分析
在本次仿真中,主要验证算法在曲线检测过程中只能对基线为零的曲线进行有效检测,对于基线非零的曲线在参数空间中无法进行有效积累。本仿真分为两部分,在第一部分中根据式(19)产生一条基线为零的峰值曲线,并对其进行曲线参数检测,零基线处峰值曲线参数如表1所示;第二部分根据式(18)产生3条基线不为零的峰值曲线,这3条曲线与第一部分曲线的幅度和初相一致,并进行曲线参数检测,非零基线处峰值曲线参数如表2所示。仿真图如图9和图10所示。仿真第一部分中由图9和图10 可知:对于基线为零的曲线,算法在参数空间对其可进行有效积累,图10(a)为参数空间积累结果,在曲线对应参数处有明显的峰值出现,将图10(a)向幅度维和相位维投影可得到图10(b)和图10(c),可知,曲线的幅度和初相检测结果与表1中仿真参数一致。

表1 零基线曲线仿真参数

表2 非零基线曲线仿真参数
仿真第二部分中由图11和图12可知:对基线非零处的峰值曲线,算法在参数空间对其无法进行有效积累,在图12参数空间中没有峰值出现。
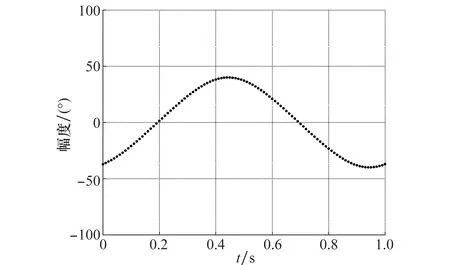
图9 零基线处峰值曲线仿真Fig.9 Simulation of peak curve at zero baseline
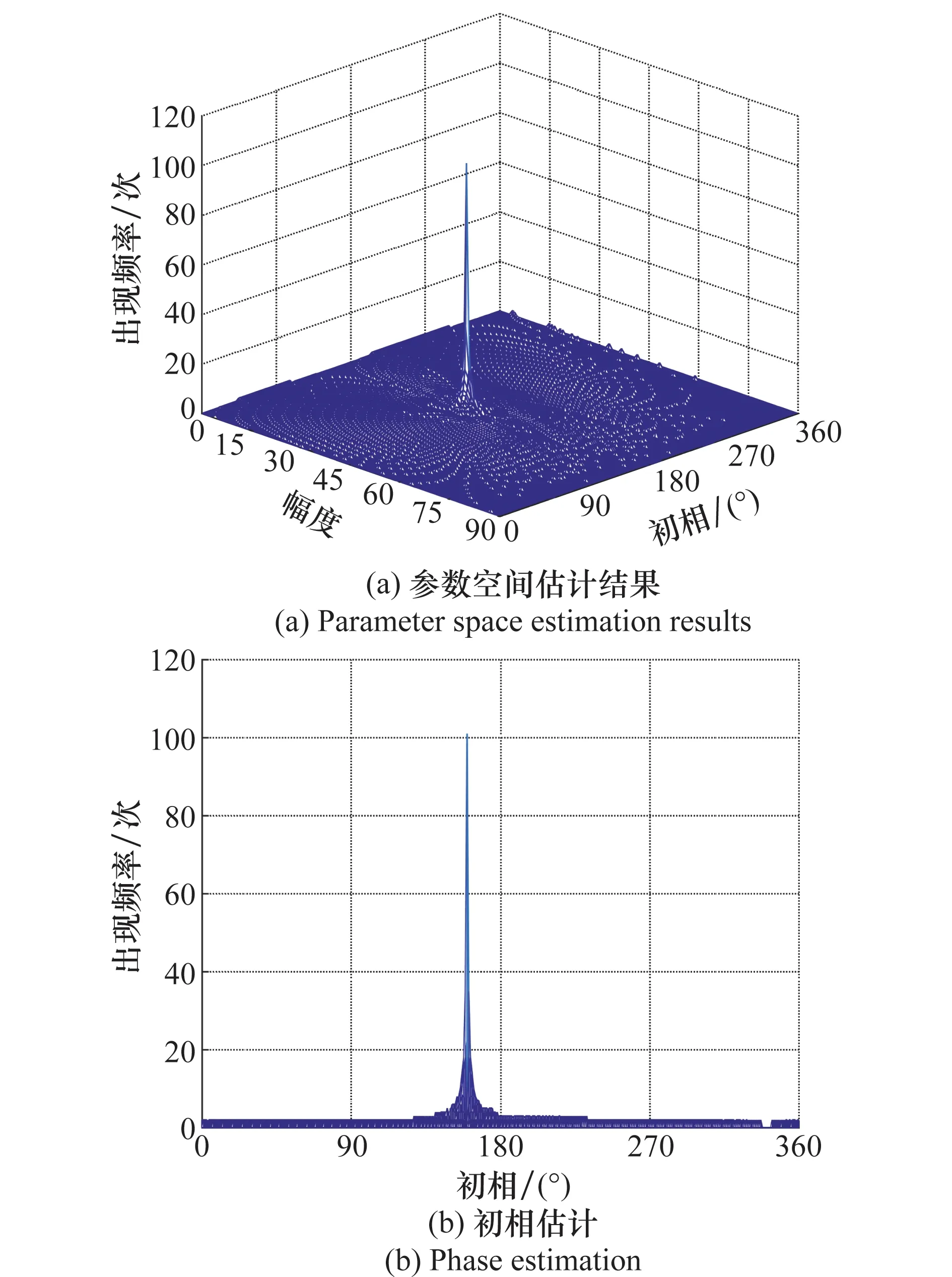
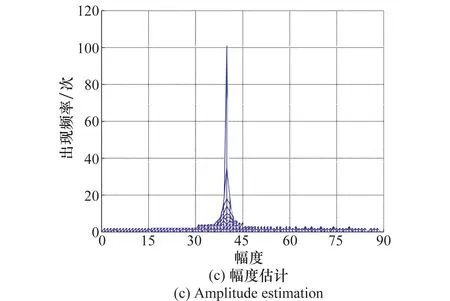
图10 零基线处峰值曲线参数空间处理结果Fig.10 Processing result of parameter space in peak curve at zero baseline
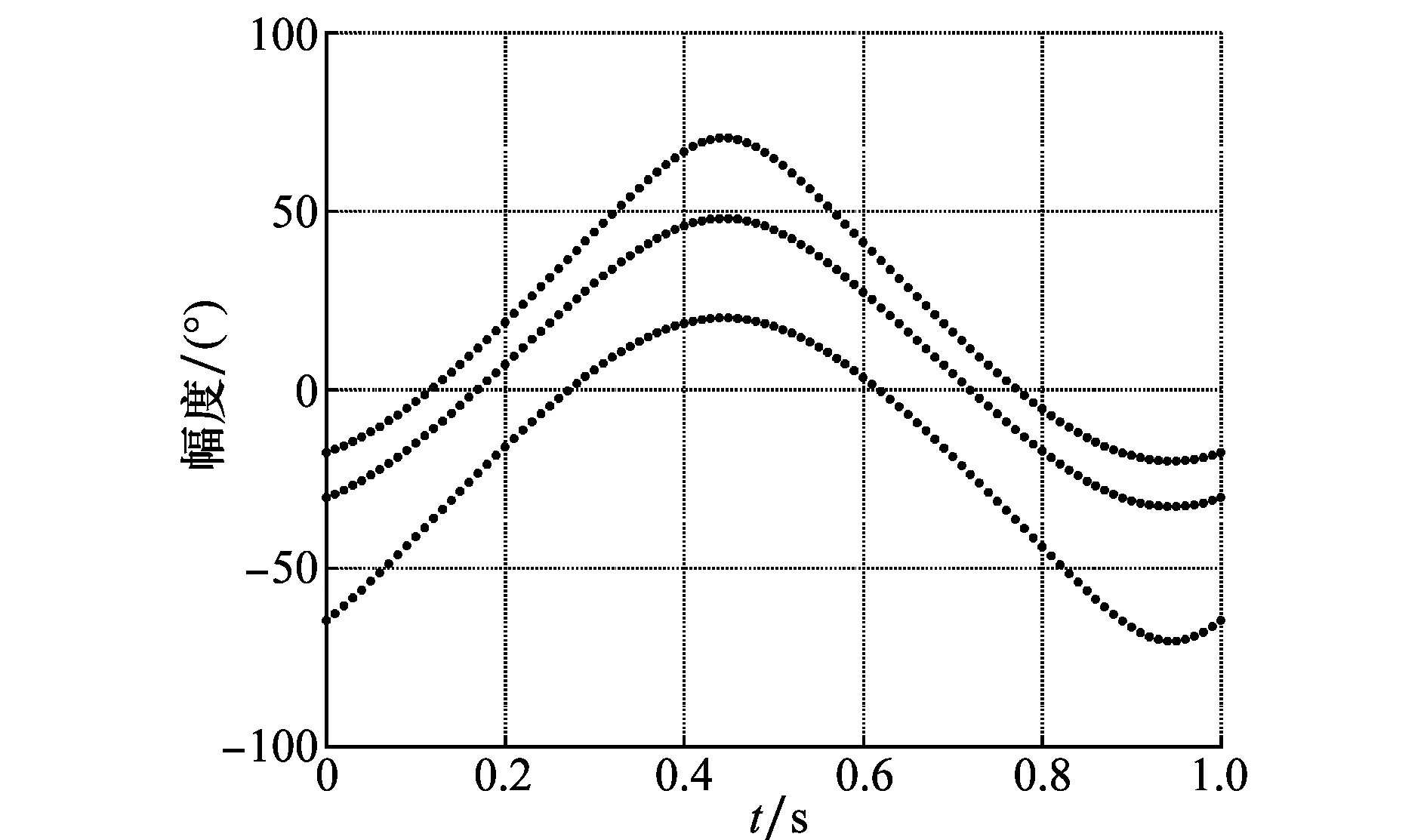
图11 非零基线处峰值曲线仿真Fig.11 Simulation of peak curve at non zero baseline

图12 非零基线处峰值曲线参数空间处理结果Fig.12 Processing result of parameter space in peakcurve at non zero baseline
根据第2节分析可知,基线为零的峰值曲线对应的是信号源的真实角度信息,基线不为零的峰值曲线对应的是信号源的模糊角度信息,因此算法能出检测出真实角度信息,同时消除了角度模糊的影响。
3.2 阵元间距半波长仿真分析
本仿真主要验证算法对多信号源参数检测的有效性,系统参数及目标参数如表3和表4所示。
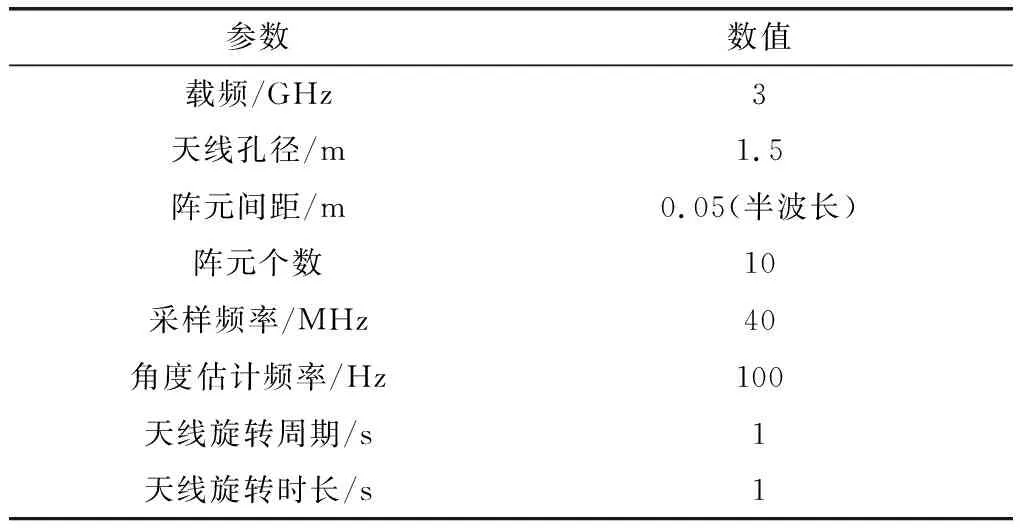
表3 系统仿真参数
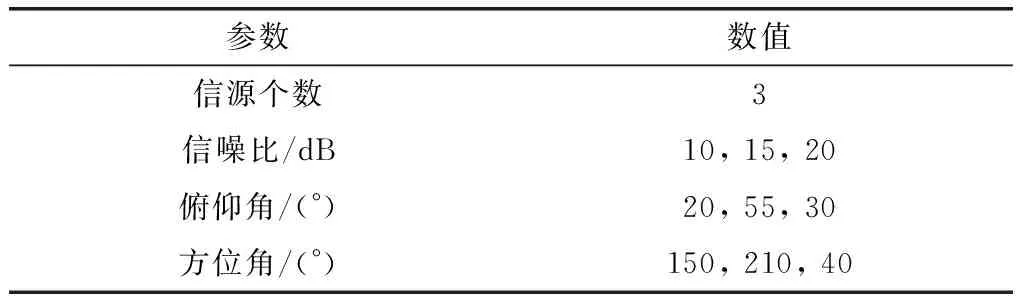
表4 目标参数
图13、图14给出了算法在阵元间距为半波长时对多目标的角度估计。一维谱估计使用MUSIC算法实现,快拍数为200。如图13所示,3条峰值曲线的基线2k/m=0。参数空间积累结果如图14(a)所示,参数空间积累中出现3个信号的峰值,各峰值对应坐标为(20°,150°)、(30°,40°)、(55°,210°),其中横坐标为峰值曲线的幅度对应信号源的俯仰角,纵坐标为曲线的初相对应信号源的方位角,由此根据坐标点位置即可得到信号源二维角度信息,避免了参数匹配问题。图14(b)和图14(c)是图14(a)在方位维和俯仰维的投影。

图13 d=λ/2时天线转动一周的谱估计峰值Fig.13 Spectral estimation peak of antenna rotation at array element d=λ/2
3.3 阵元间距多倍半波长仿真分析
本小节分析算法在测向结果有角度模糊时在参数空间积累的有效性,仿真利用Matlab对整个信号处理流程进行仿真,系统参数与目标参数如表5和表6所示。
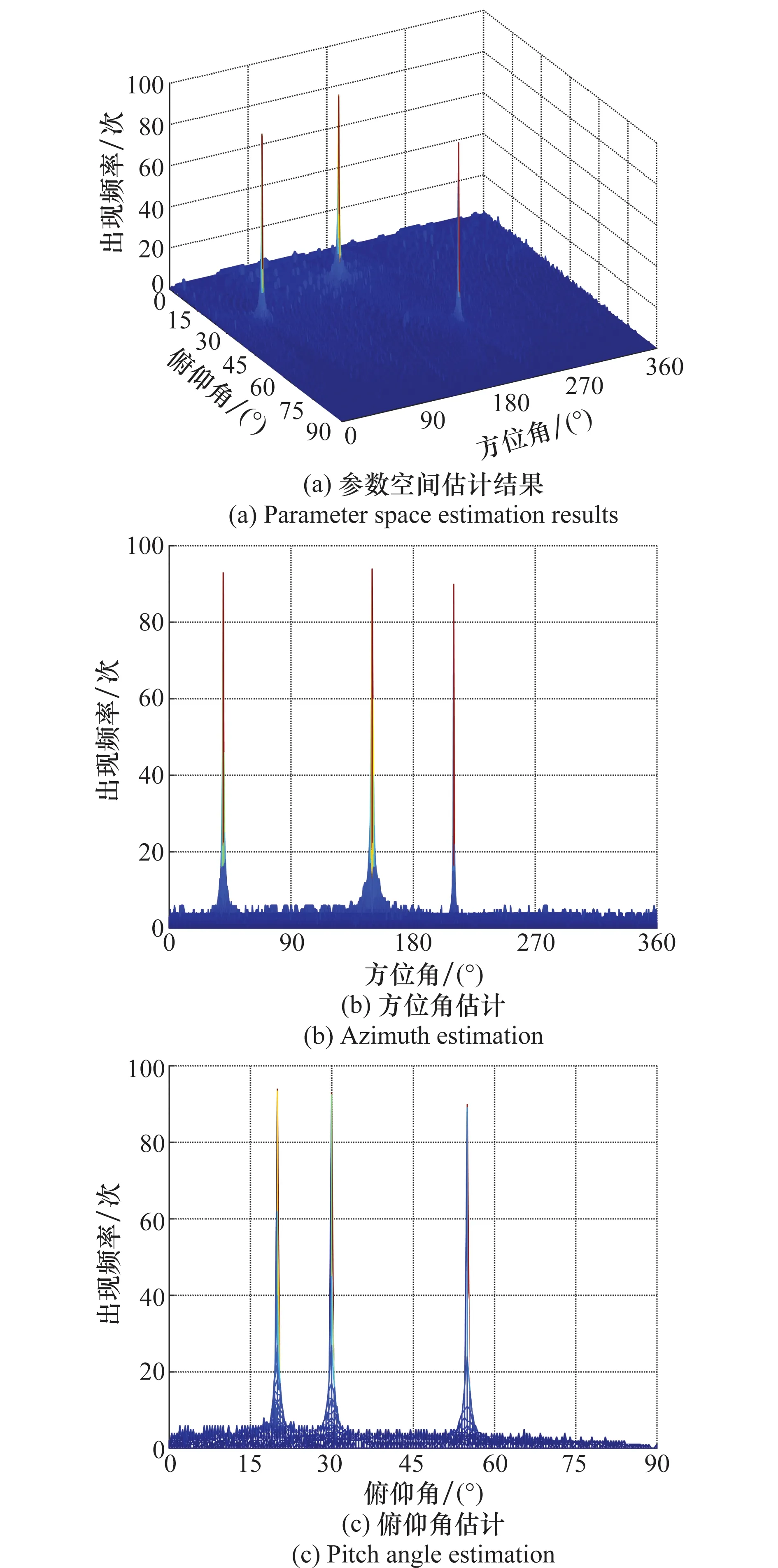
图14 阵元间距半波长时参数空间处理结果Fig.14 Processing result of parameter space in half wavelength of array element

参数数值载频/GHz3天线孔径/m5阵元间距/m0.5(10倍半波长)阵元个数10采样频率/MHz40角度估计频率/Hz300天线旋转周期/s1天线旋转时长/s1
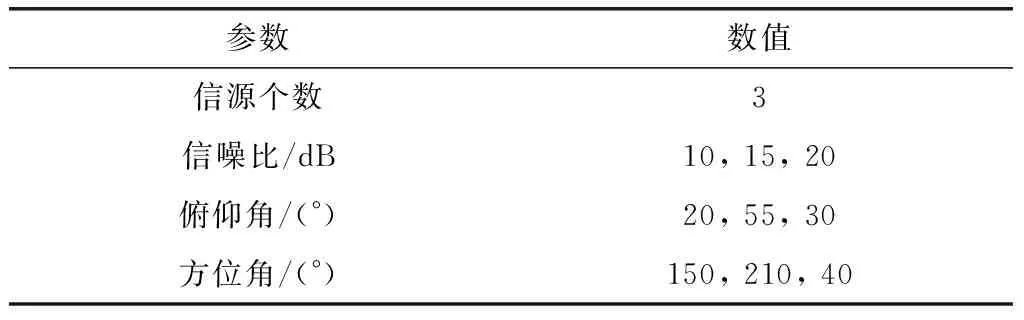
表6 目标参数
图15、图16给出了本文方法在阵元间距为多倍半波长情况下对多目标二维角度的估计验证。一维角度估计使用MUSIC算法实现,其中MUSIC算法快拍数为200。

图15 d=10(λ/2)时天线转动一周的谱估计峰值Fig.15 Spectral estimation peak of the antenna rotation at array element d=10(λ/2)
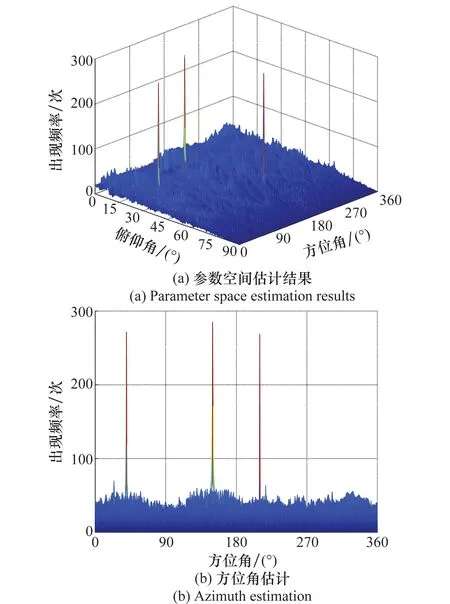
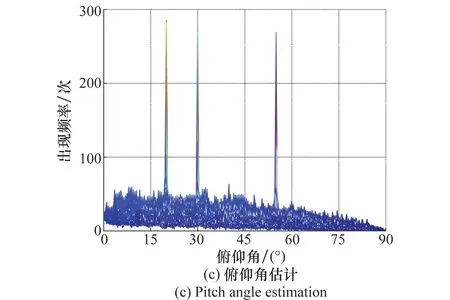
图16 阵元间距多倍半波长时参数空间处理结果Fig.16 Processing results of parameter space in multiple wavelength half space of array elements
由图15可见,天线相对目标角度成多条三角复合函数曲线变化,其中,阵元间距为10倍半波长,因此对于同一个目标会产生多个角度模糊。由式(18)可知,对于同一个信号源而言,峰值曲线有两种,分别为真实峰值曲线与角度模糊峰值曲线,这两种曲线的初相和幅度是相同的,区别在于基线分布的位置不同,真实峰值曲线分布在基线为零的位置,即2k/m=0,而角度模糊峰值曲线的基线分布在非零处,即2k/m≠0。
在曲线参数检测过程中:①对真实峰值曲线进行了有效检测,参数空间积累结果由图16(a)所示,参数空间积累中出现3个信号峰值,3个峰值所处位置的坐标分别为:(20°,150°)、(30°,40°)、(55°,210°),可以准确分辨各目标的角度信息,无需对信号源进行角度匹配。图16(b)和图16(c)是图16(a)分别在方位维和俯仰维的投影。②对于基线位置非零的角度模糊峰值曲线,在投影到角度参数空间时不能产生有效积累,在参数空间中以小毛刺的形式存在,形成不了峰值,由此避免了角度模糊的影响。综上本文所提处理方案可以有效解决测向过程中出现的角度模糊问题。
3.4 性能分析
在本小节中,利用本文所提方法与互质基线解模糊方法、传统旋转干涉仪方法和阵元间距为半波长的均匀线阵MUSIC测向方法进行对比,为了便于分析,通过单目标蒙特卡罗仿真实验进行说明,多通道旋转干涉仪系统参数、互质基线干涉仪系统参数、传统旋转干涉仪系统参数、阵元间距为半波长的均匀阵列系统参数和目标参数、分别如表7~表11所示。

表7 多通道旋转干涉仪系统仿真参数

表8 互质基线系统仿真参数
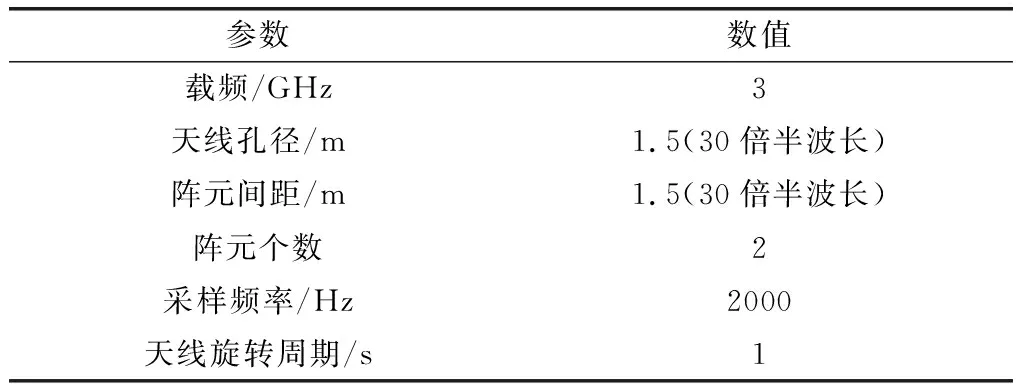
表9 旋转干涉仪系统仿真参数

表10 半波长均匀线阵系统仿真参数
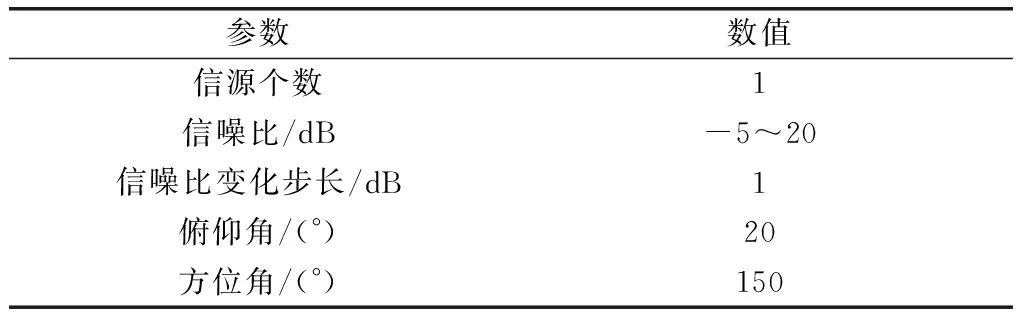
表11 目标参数
输入信噪比(signal-to-noise ratio, SNR)变化范围为-5~20 dB,步长为1 dB,对每一个信噪比进行1 000次蒙特卡罗实验。
图17为4种算法的测向均方根误差(root mean square error,RMSE)的比较,由仿真结果可得:①基于多通道旋转干涉仪的方法利用子空间类测向算法进行处理性能优于互质基线解模糊方法和传统旋转干涉仪方法,且对信噪比的要求较低;②本文所提方法为稀疏布阵,阵元个数少,因此性能与阵元间距为半波长的均匀线阵相比较差。③本文所提方法为均匀稀疏布阵,对一定频率范围内的信号均可处理,对于低频信号避免了由于阵元间距过小造成的互耦现象,对于高频信号带来的测向模糊,本文所提处理流程可有效解决。本文所提方案可适应电子侦察中对宽频程信号侦测的要求。
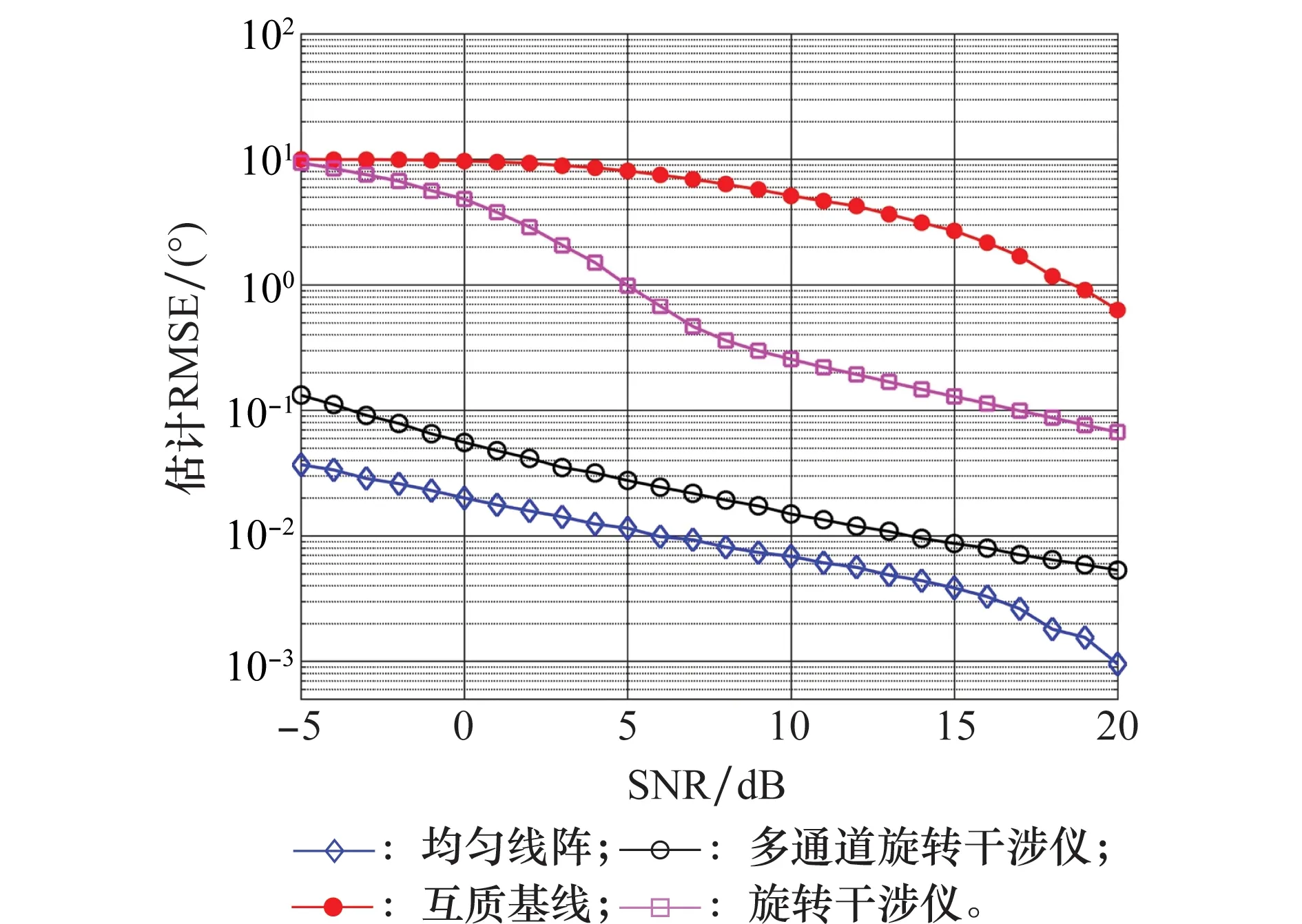
图17 4种方法在不同SNR下的性能对比Fig.17 Performance comparison of four methods under different SNR
4 结束语
本文采用的将传统测角方式与图像检测相结合的目标检测算法解决了在星载平台下大口径天线测向模糊的问题,同时可以应用到卫星编队中。优点如下:①通过阵列信号的处理方式,实现了多个目标的分辨,准确度高,对SNR的要求大大降低;②利用旋转基线的方式角度模糊呈三角曲线规律变化,避免不同目标间的角度匹配问题;③利用曲线参数积累的方式估计目标角度信息,运算复杂度低,可以进行并行处理,具有一定的实时性,便于工程实现。仿真实验证明本文方法的有效性。针对稀疏天线角度解模糊问题,将在接下来的科研工作中进一步展开研究。

