自适应伪相干值改进的InSAR干涉图Goldstein滤波算法
李世金 张书毕 张秋昭 高延东
(中国矿业大学环境与测绘学院,江苏徐州221116)
合成孔径雷达干涉测量技术(Interferometric synthethic aperture radar,InSAR)是一种用于提取地表三维变化信息的空间对地观测技术,是传统合成孔径雷达遥感技术与无线电磁波干涉测量技术的有效融合。该技术不仅具有成本低、近连续性的特点和远程遥感观测的能力[1],还能够全天候、全天时、高效率地获取大面积的地面高精度三维信息。因此,InSAR技术在近些年得到了快速发展,在矿区沉陷监测[2]、城市沉降[3]、地震形变[4]、火山运动[5]、山体滑坡[6-7]及冰川运动[8]等方面也展现出了强大的技术优势。在InSAR技术的实际应用中,相位解缠的结果将直接决定着地面高程信息的获取精度,而相位解缠的结果又与干涉图的质量密切相关,因此,研究干涉图的滤波算法对于进一步提高干涉图的质量乃至InSAR技术的应用效果大有裨益。
InSAR干涉图滤波算法主要有空间域滤波及频率域滤波2类。其中,空间域滤波最常用的是圆周期均值滤波与圆周期中值滤波,主要根据干涉图的周期性特点,利用局部统计特性来实现滤波。在此基础上,圆周期加权中值滤波算法被提出,该算法融合了上述2种算法的优点,滤波效果有了一定程度提升。上述算法的滤波效果与滤波窗口的尺寸存在着密切的关系,随着滤波窗口的增大,噪声去除效果越来越好,但相应的图像分辨率损失严重。为此,郭交等[9]将基于局部区域增长算法的窗口自适应获取方法应用到滤波算法中,通过选取均值像素的滤波样本,以提高滤波的自适应效果;易辉伟等[10]提出了改进的梯度自适应滤波算法,根据不同方向的相位梯度信息来获取相应像素点的加权系数,进而实现自适应滤波。频率域滤波算法则是依据傅里叶变换原理将干涉图从空间域转换至频率域,在频域内依据相位噪声和信号的频谱特性进行滤波处理,极大提升了相位信息的保留能力。最经典的滤波算法为Goldstein滤波[11],该算法对具有一定重叠效果的相位块在频率域采用平滑滤波器处理后,并用固定的滤波参数对其功率谱进行处理。鉴于滤波参数的选取具有一定的主观性,Baran等[12]利用相干值均值代替滤波参数,使其能够根据干涉图的相干性实现自适应滤波;Suo等[13]为了进一步提升该算法相位噪声的抑制能力,利用相干值的平方值代替相干值均值,在相同的滤波窗口下进一步增强了滤波强度;为进一步提升自适应效果,Zhao等[14]利用伪相干值均值代替相干值均值作为滤波参数,并进行迭代处理,在一定程度上避免了偏置样本一致性对滤波参数的影响;Liu等[15]提出了分窗口模型滤波算法,将改进后的经验模型分解(Empirical mode decomposition,EMD)算法[16]与Goldstein滤波算法[17]作为不同窗口的滤波模型。
上述改进滤波算法虽然在一定程度上提升了算法的滤波性能,但总体上无法有效兼顾相位噪声抑制及相位信息保留两方面。因此,本研究采用伪相干值对Goldstein算法的滤波参数进行进一步优化,使其能够根据不同阈值选取不同的自适应模型,进而自适应确定最优滤波参数,并根据阈值自适应确定平滑窗口尺寸,对干涉图的功率谱进行平滑处理。
1 干涉图滤波算法
1.1 Goldstein滤波
Goldstein滤波[11]首先将干涉图划分为若干个相互重叠的相位块,然后依据傅里叶变换将其转换至频率域,对其功率谱进行相应的平滑处理:
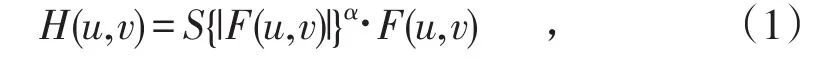
式中,S{*}为平滑算子;F(u,v)和H(u,v)分别为滤波前后的频率域干涉图;(u,v)为频率域中干涉图中某像素点的坐标值;α为滤波参数,α∈[0,1]。
当α=0时,S{|F(u,v)|}=1,表明无滤波效果;当α=1时,S{|F(u,v)|}表示由矩形平滑窗口构成的低通滤波器,表明滤波效果非常强。此外,较大的相位块尺寸和高滤波参数α值,有利于增强干涉图的相干性;相位块相互重叠(重叠度不宜小于75%)有助于减弱干涉图边界处的不连续性。
考虑到干涉图中相位噪声分布的不均匀性,如果对整个干涉图采用固定的α值进行滤波,易降低滤波的自适应性,可能会在高相干地区存在过滤波,而在低相干地区存在欠滤波的现象,因此难以选择合理的全局滤波参数α值。对此,Baran等[12]采用相干值的均值代替α值,使得干涉图非相干性区域的滤波程度强于相干性区域:

Zhao等[14]利用伪相干值均值代替α值,相对于Baran滤波算法在一定程度上避免了偏置样本一致性对α参数估计的影响,其伪相干值(Pc)可通过下式求取:

式中ϕi为第i个像素的复数相位值;n为像素点数量。
1.2 改进后的滤波算法
为进一步提高Goldstein滤波算法的自适应性,本研究对获取的伪相干值进行进一步优化,首先对大于阈值T的伪相干值进一步增大,对小于该阈值的伪相干值进一步减小;然后将当前滤波窗口中改进后的伪相干值均值作为滤波参数,并根据设定的阈值自适应确定平滑窗口尺寸。为此,构建的改进后的伪相干系数的取值模型为

为有效兼顾滤波算法在噪声抑制及相位信息保留两方面的效果,需要有效确定α值,本研究构建了随伪相干值(Pc)自适应变化的α取值模型。
当Pc≥T时(0<β<1),模型为

式(5)、式(6)中T值选取依据为:当 -Pc较大时,即干涉图质量整体较好,滤波重点应为提升相位细节信息,故T值应相对较小;当-Pc较小时,滤波重点应为提升去噪效果,故T值应相对较大。本研究经过仿真试验,构建的λ取值模型为

为进一步提升算法的自适应滤波效果,依据上述确定的阈值进一步自适应确定平滑窗口尺寸。当默认平滑窗内的伪相干值均值于小阈值时,对其平滑窗口尺寸进行增大处理,直至窗口内的伪相干值均值大于阈值为止,以提高算法在低相干区域的降噪能力。随后采用二维傅里叶变换后的平滑窗口对获取的相位块的功率谱进行平滑处理[13],并运用改进后伪相干值进一步确定滤波参数,最终获取滤波后的干涉相位。改进后的Goldstein滤波算法可表述如下

式中,|*|m×m为傅里叶变换后的平滑窗算子;m为窗口尺寸。
2 算法试验
2.1 TerraSAR数据试验
本研究采用TerraSAR数据进行滤波分析,结果见图1、表1。


注:原始含噪声干涉图中残差点有26 137个。
分析图1可知:在高相干性区域4种滤波算法的滤波效果基本相似,而在中部及右下角相干性较低的区域,本研究算法的去噪效果明显优于其余3种算法。
分析表1可知:4种滤波算法的噪声抑制能力均较理想,其中Goldstein滤波与Zhao滤波处理后的干涉图中剩余的残差点数量较接近,相应的噪声去除率分别为80.74%、80.40%;Baran滤波效果略优于前2种算法,噪声抑制率约82.24%;本研究算法的噪声抑制率达到88.64%,并且该算法的EPI明显高于其余3种算法,表明该算法不仅滤波性能较好,而且具有良好的相位保持能力。
在上述分析的基础上,采用GAMMA软件中的枝切树相位解缠模块对不同滤波算法处理后的干涉图分别开展了相位解缠工作,结果如图2所示。分析图2可知:由于残余残差点的影响,易导致解缠结果中出现大量的未解缠区域,经过本研究算法滤波后的干涉图的整体解缠效果明显优于Goldstein滤波、Baran滤波以及Zhao滤波,尤其是图中标记区域,未解缠区域明显少于其余3种算法;此外,Zhao滤波算法处理后的干涉图的解缠结果中出现了大量误差传递现象(图2(c)),本研究算法则无此现象,进一步证明了该算法的有效性。

2.2 DEM反演分析
为进一步验证本研究算法对于实测数据的处理效果,采用1组5 000×5 000的TeraaSAR/TanDEM数据进行了DEM反演分析。首先对比分析不同滤波算法对于该数据的滤波效果,然后采用GAMMA软件对其进一步处理,对不同滤波算法处理后获取的高程精度进行比较分析。
本研究采用去地势后的干涉图进行试验。分析图3、表2可知:4种滤波算法对图3(a)中标定区域的滤波效果均较好,噪声去除率依次为86.31%、86.70%、86.62%、90.51%;本研究算法滤波后的干涉图中的残余相位噪声点明显少于其余3种算法,并且该算法处理后的干涉图的EPI指数明显大于其余3类算法。
对不同滤波算法处理后的干涉图运用GAMMA软件处理后获取的地距结构干涉高程图如图4所示。依据图4提取的高程信息与SRTM高程数据的RMSE值如表3所示。


注:原始含噪声干涉图的残差点数量有33 096个。


分析图4及表3可知:经过Goldstein滤波、Baran滤波及Zhao滤波算法处理后获取的干涉高程图均出现了大量空洞现象,主要是由于残余的噪声点影响了后续的枝切树相位解缠效果,导致相位解缠后出现了“孤岛”现象,最终影响了高程信息的提取精度;本研究算法处理后获取的干涉高程图未出现该现象,并且相应的RMSE值明显小于其余3种算法。
3 结语
采用伪相干值对Goldstein滤波算法的滤波参数及滤波窗口进行了优化,TerraSAR-X/TanDEM-X数据滤波分析以及DEM反演分析表明,改进后的滤波算法在噪声抑制及条纹相位信息保持方面优于Zhao算法、Baran算法以及Goldstein算法,并且在高程信息提取精度方面也有明显优势。

