滑坡受灾结构体易损性离散元分析

毕钰璋 孙新坡 何思明 王安辉

（1.东南大学交通学院岩土工程研究所，江苏南京210096；2.四川理工学院土木工程学院，四川自贡643000；3.中国科学院山地灾害与地表过程重点实验室，四川成都，610041；4.中国科学院·水利部成都山地灾害与环境研究所，四川成都，410041；5.中国科学院青藏高原地球科学卓越创新中心，北京，100101）

1 项目背景

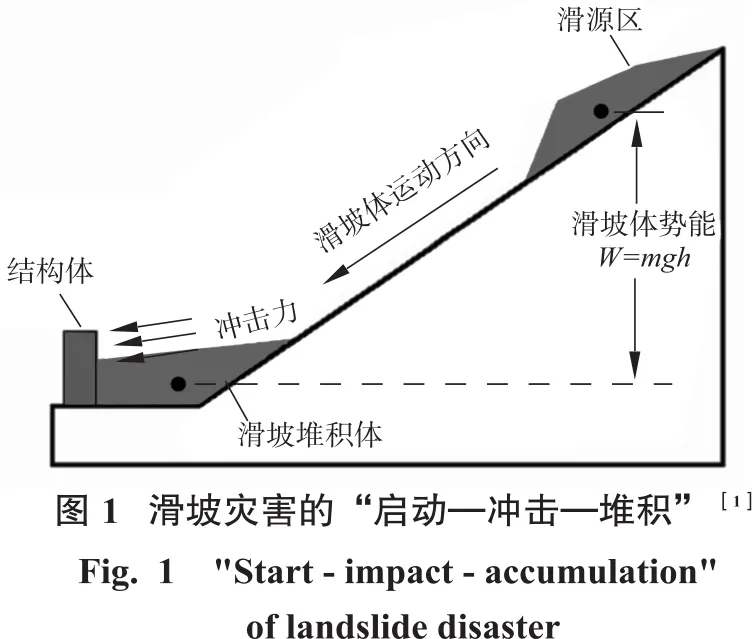
滑坡灾害是工程地质中的一种常见的灾害形式，其中又以高速远程滑坡的破坏程度尤甚，它的运动过程伴随着巨大的动能并且对所经过的结构体造成了巨大的冲击和破坏［1-2］，图1中显示的就是滑坡灾害从发生到冲击结构体直至堆积的整个过程的示意图［3］。滑坡灾害体对结构体的冲击作用以及破坏程度在地质灾害的研究领域中一直被认为是评价灾害程度的一个重要指标。传统的滑坡灾害的风险研究当中通常用灾害体滑移的速度及其运动的距离来作为评判灾害破坏程度的一个重要标准。然而在现实的滑坡灾害案例中，灾害的破坏程度往往取决于其对居民区的房屋建筑、道路、桥梁等结构体所产生的破坏程度［4］（见图2）；而研究灾害体和结构体之间的动力响应则属于滑坡易损性的研究范畴：各国学者已经证明了易损性分析可以预测结构体在遭受不同滑坡灾害体的作用下发生各级破损的概率，对于挡土墙以及抗滑桩的设计、加固和维修决策具有重要的应用价值［5-8］。

在研究滑坡易损性的过程当中，实证分析、实验模拟和数值计算是我们3种常见的做法。国内外学者对此做出了大量的工作：Mileti团队以哥伦比亚的Nevado Del Ruiz灾害为实例分析了灾害体和建筑物的动力响应［9］。Toyos在研究Vesuvius的某次滑坡灾害中提出了可以系统地评估建筑受损程度的一套方案［10］。M Silva［3］通过实证研究提出了评价灾害易损性的3个指标：结构体的抗破坏程度（BR），滑坡的规模（LM）以及结构体的经济价值（EV），并提出了一套完整的灾害损失评价方法。Shi［11］通过离散元数值模拟的方法研究了不同摩擦系数条件下滑坡体与结构体的动力响应过程，并给出了摩擦系数与判定灾害易损性的相互关系。虽然前人做了很多相关的研究工作，但大部分工作仍停留在宏观的范围，给出的评判灾害损失的方法与真实的损失仍存在一定的差异。虽然有学者研究了灾害体和结构体之间的动力响应关系，但大部分没有考虑实际情况，比如有学者考虑了坡面摩擦系数与灾害易损性之间的关系［11-12］，然而现实的灾害发生过程中，灾害体滑动时其坡面的摩擦系数大体是不变的。

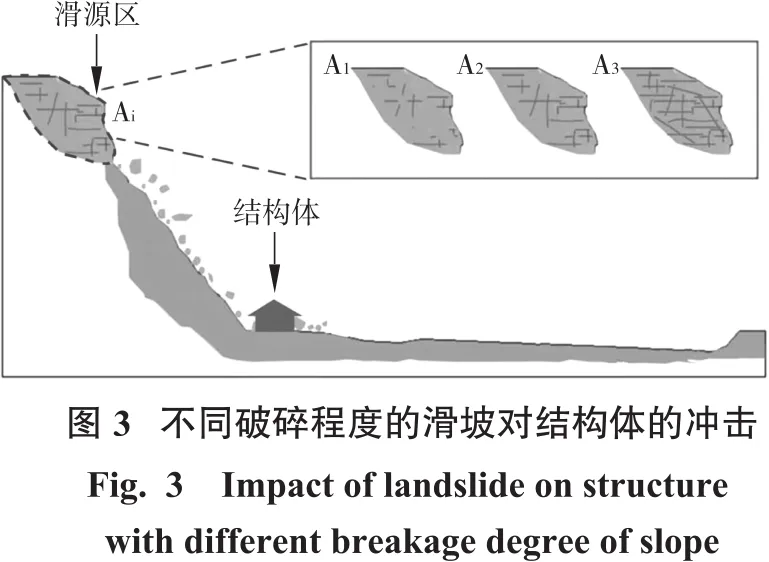
相对于基于坡面摩擦系数的结构体易损性研究，笔者认为基于灾害体破碎程度的结构体易损性研究更具有实际的工程意义。图3显示了不同破碎程度的滑坡体对结构体的冲击示意图。Iverson指出在泥石流、碎屑流等灾害体中不同的颗粒级配会对其流动性产生很大的影响［13-14］，Jiang通过实验验证了这一理论并给出了不同颗粒尺寸条件下灾害体的运动机理，并指出颗粒之间的摩擦系数以及颗粒本身的尺寸大小是影响其运动机理的主要原因［15-16］。基于此，本项目致力于研究滑坡体破碎程度对其破坏程度的影响，通过探究不同破碎程度的滑坡体和结构体之间的动力响应来得出相应的规律性的结论，并通过这些结论完成基于滑坡破碎程度的易损性的评价。

2 滑坡破碎程度和易损性评价的关系

在众多的易损性研究中，最主要的研究方法包括概率统计法和易损性评估法——这些方法的主要研究手段是工程实例分析［17-18］。如图1所示，在离边坡坡角的一定距离是一个结构体，它所受的破坏程度取决于边坡的几何形状及其地质条件；然而即使是在相同的边坡条件下，不同类型（形状、材料）的结构体将很可能受到不同程度的冲击和破坏。因此，结构体的最终破坏程度将取决于灾害体及结构体本身的共同作用——这就意味着在灾害风险评估中仅仅分析边坡稳定性是远远不够的，结构体的破坏程度应当在易损性的研究中被充分考虑进去。在滑坡灾害中，灾害体的冲击力和其滑动速度呈正相关，并且与其滑坡体的破碎程度有关。

在结构体设计的过程中，其受到灾害体冲击破坏时的临界值通常是判别结构体“可靠”和“不可靠”的非常关键的因素，并且需要大量的统计数据对其进行理论支持。然而，当随机变量不服从正态分布时，极限状态方程是非线性，这就给易损性的判定带来了不便。鉴于破碎程度对滑坡灾害的程度影响，式（1）给出了一个简单的判别方法：

其中，S是灾害体施加在结构体上的外部载荷的总和；F是结构体本身的强度；f代表影响滑坡灾害体的破碎程度的系数——用灾害体的当量冲击力和结构体抗冲击强度的比值来表示。如图4所示：当f大于1时，结构体破坏；当f介于0和1之间，结构体保持稳定。

3 离散元方法的基本思路

离散元方法是基于分子动力学（molecular dynamics）而发展起来的一种方法。之后Cundall于1971年提出了适用于岩土力学的离散元方法［19］，并于1979年和Strack［20］在共同创立的一种基于二维圆盘和三维圆球排列建立数值模型的方法（PFC-2D/3D），其分析具体问题时整个模型的构建是主要以离散的“球（圆盘）单元”、以及“墙单位”组建起来的。其颗粒流模型的假设包括以下几个方面：

（1）球体被视为刚性体。

（2）接触发生在几近非常小的一个范围。

（3）接触部分允许有叠加并且其接触行为假设为“柔性接触”。

（4）叠加部分遵循接触力的“力—位移”法则。

（5）颗粒间的接触允许有粘结。

（6）所有颗粒都是球体（圆盘）形状。

本次滑坡易损性的数值模拟研究运用了二维离散元方法，基于PFC-2D的平台，对不同破碎程度的滑坡灾害进行了详尽的研究。本次研究过程中使用的模型是“滑动模型”，它允许颗粒在抗剪强度范围内发生滑动。滑动模型是通过两接触体间最小摩擦系数 μ定义的，如果颗粒之间重叠量Un小于或等于零，则令法向和切向接触力等于零。发动滑动的判别条件为：

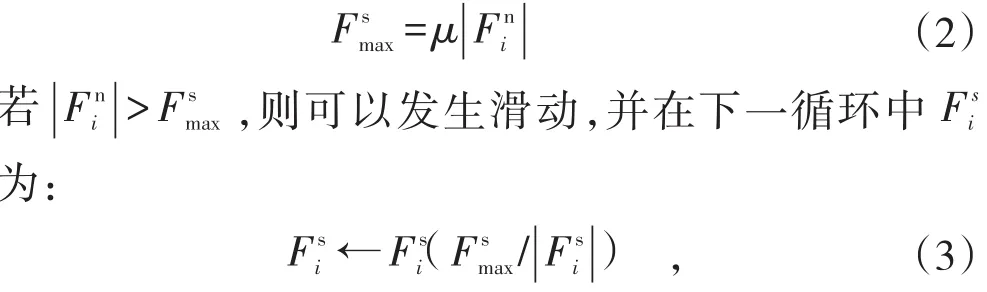
4 工程算例及模型建立

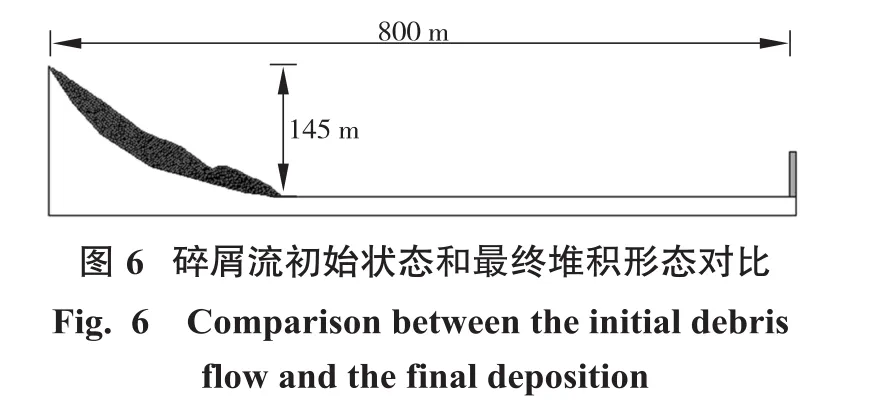
本项目采用了云南省肩舆山的一处典型的高陡滑坡（Palankeen Mountain landslide）来作为本次研究的工程算例［11］。该处滑坡为一处典型的高速滑坡，如图5所示，该滑坡位于一个沟谷上方的斜坡带：该沟谷处的边坡坡角低至27°，高至48°，坡角值在这个范围内波动；并且大部分地段出现了大于45°的陡坡情况。边坡的整体形态呈不规则的近椭圆形态：沿公路的走向长度接近80～90 m，沿坡体下滑方向的长度接近250 m；边坡后缘的高程约2 745 m，前方断裂启动处的高程约2 600 m，两者之间的高程差约为145 m。该处滑坡为节理裂隙化的岩土体滑坡，现场调查的灾害体主要由大量碎石组成，并包含有一定量的“粘土—砾石”混合物。整个滑坡的平均厚度为15 m，其总的滑坡体积大约为3.8×105m3。

如图6所示，图中表示的是在PFC2D中生成的理想滑坡模型：模型的尺寸严格按照图5中的尺寸建立，灾害体由颗粒模型组成，坡面由“墙单元”组成。为了实现不同破碎程度的灾害体模型，在相同体积灾害体的条件下，采用不同大小的颗粒粒径来表示其破碎程度：0.3 m、0.5 m、0.8 m、1.0 m。本次模型的建立分为3个步骤完成：研究所用模型的设定、数值模拟中的滑坡灾害体的参数选取、数值模拟中的边坡坡面的参数选取。

4.1 研究所用模型的设定

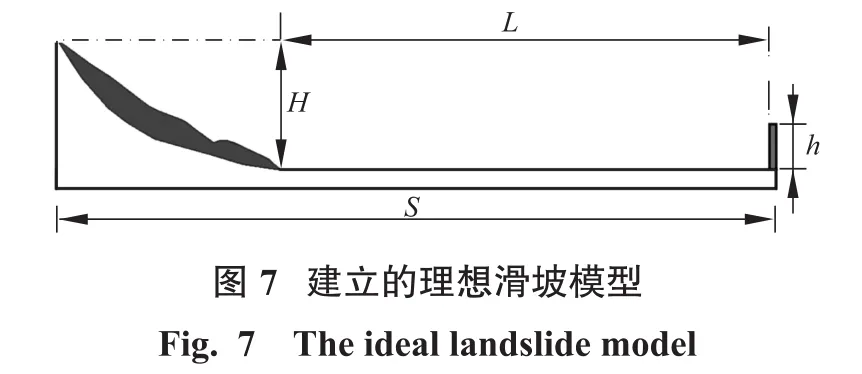
滑坡的真实剖面形状和几何尺寸如图5所示，然而在本次研究过程中，笔者对滑坡的模型做了一个理想性的假设：假设边坡滑移面底端到结构体之间为水平的地形条件（如图7所示）。由于本次研究的目的是滑坡破碎程度对其易损性的影响，因此忽略复杂的地形条件有利于抓住研究过程中的主要矛盾，并且对原始地形模型进行的简化有助于对模拟的结果进行定量化的对比，比如灾害体的运动距离等。

如图7所示，结构体距离坡脚处的距离为L，滑坡的高程为H，假设结构体高度h足够高并且可以拦截所有的滑坡体——本次研究所采用的h为40 m。该处灾害体在重力作用下滑移，对此我们进行了两种不同条件下的模拟：如果L小于灾害体的滑程，则灾害体将对其滑程范围内的结构体进行撞击；如果L大于灾害体的滑程，则不同条件灾害体的动能将反映在其运动距离上。通过研究灾害体的滑程及其和结构体之间的动力响应情况来综合判定不同破碎程度下的滑坡灾害的运动规律。

4.2 数值模拟中的滑坡灾害体的参数选取

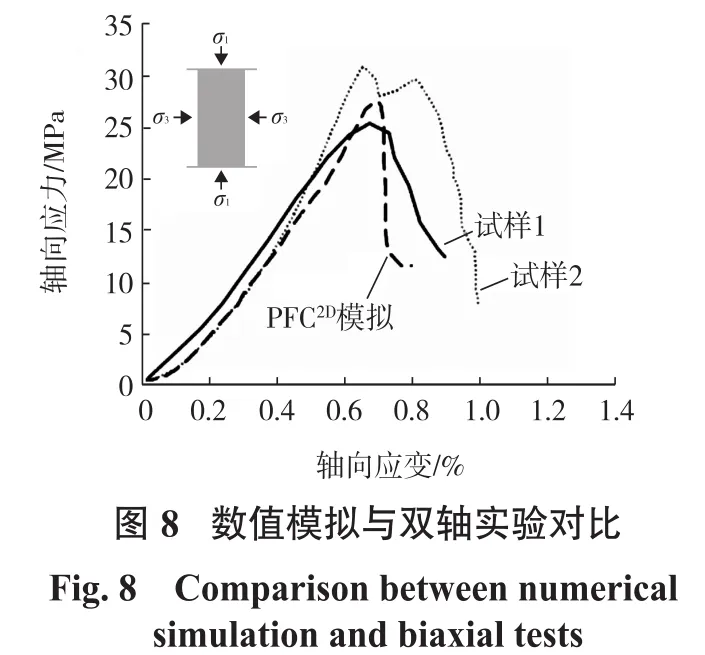
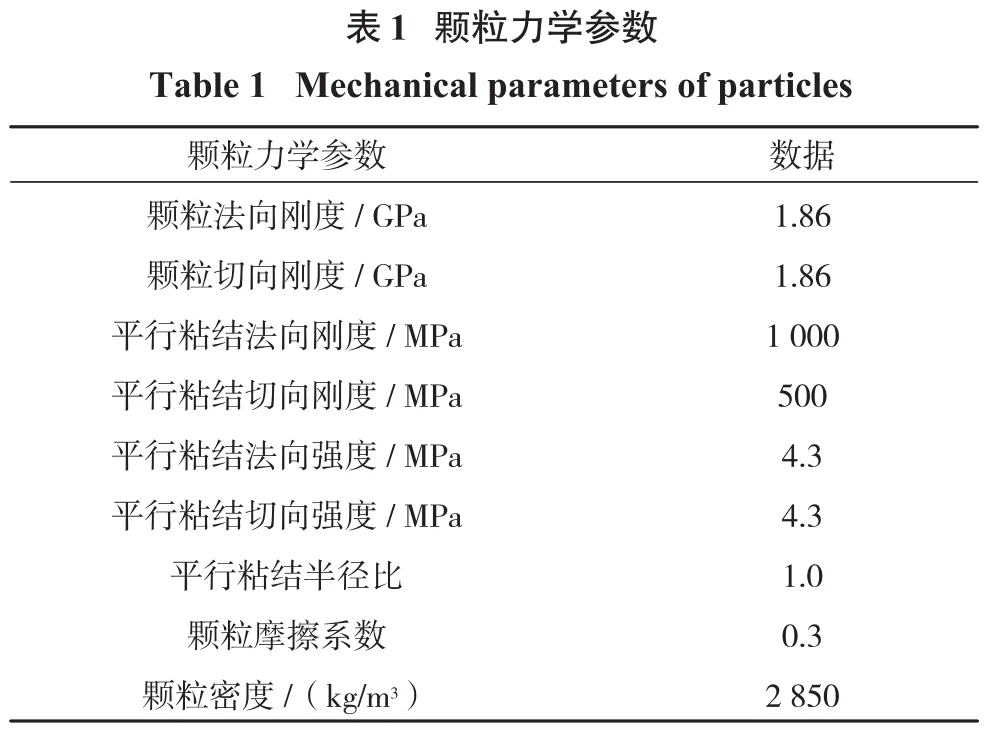
在离散元方法中，材料的宏观运动行为取决于颗粒间接触的微观力学参数。然而对于参数的选取却没有一个完全有效的方式。较多的研究方式是通过物理模型和数值模型的破坏模式相匹配，从而确定其力学参数。由于没有完备的理论依据来确定宏观条件下的运动过程和颗粒力学参数之间的选取关系，因此我们在前人对该滑坡研究时参数选取的基础上，通过反复的双轴压缩数值模型实验（见图8）来观测应力-应变曲线，以期使其与实际的物理实验相匹配。本次模拟过程参数的选取主要通过2个途径来获得：①来源于前人的参数，Shi［11］在使用离散元方法研究该处灾害的同时，对灾害体的参数进行了详细的反演；②通过数值模拟双轴压缩试验的方法对其中的一些参数进行了修正。表1为本次研究中所使用的力学参数。

4.3 数值模拟中的边坡坡面的参数选取

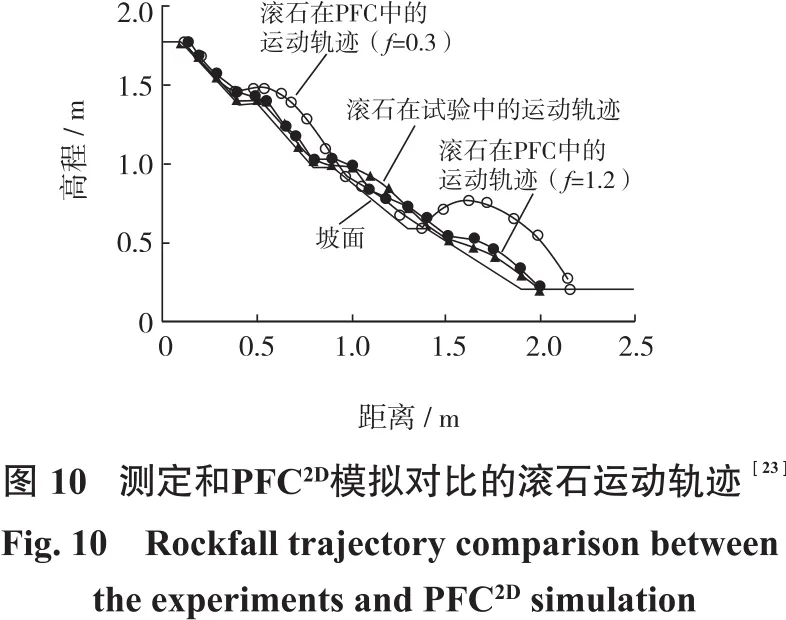
众多学者在研究滑坡灾害的过程中，喜欢将边坡坡面的摩擦系数考虑进去，从而研究不同坡面摩擦系数对滑坡灾害体运动距离的影响；然而在大多数情况下，边坡坡面的摩擦系数是一定的——即自然条件下的坡面摩擦系数的主要决定因素是植被的覆盖率。根据现场勘查和现场采样，Bi［21］设计了图9所示的试验，让滚石从试验装置的“自然坡面”顶端滑落，观测并记录滚石的运动轨迹，然后通过PFC2D反演参数，通过对比二者的滚石运动轨迹，进而得到“自然坡面”条件下的摩擦系数。

通过二者的运动轨迹对比可以发现，在PFC22DD的摩擦系数取值为1.2的条件下，室内试验和数值模拟的运动轨迹是极其相似的（如图10所示）。因此，在本次研究过程中，坡面的摩擦系数引用前人的研究成果，并将摩擦系数取值为1.2。

5 结果分析

本次研究分3个部分进行：首先将滑坡的运动路径设定得足够长，用以研究不同破碎程度的滑坡的滑程；然后在滑坡运动范围内设置结构体挡墙（H的取值分别为0，20，50，80，100，150 m），用于拦截灾害体，并研究灾害体与结构体之间的动力响应情况。

5.1 灾害体破碎程度对滑程的影响

图11显示了不同破碎程度的滑坡在相同坡面条件下的滑移距离对比。通过图11可以发现粒径为0.3 m的条件下（图11（a）所示），灾害体重心的移动距离为161 m。随着粒径的增大，灾害体重心的移动距离也慢慢增大。当粒径达到1.0 m时，灾害体的重心移动距离为435 m，几乎为0.3 m粒径条件下的3倍。通过对比发现：越是破碎程度较大的滑坡灾害体，其流动性越差；越是块体较大的灾害体，其流动性越强。这是因为在灾害体运动过程中，其内部的颗粒会相互碰撞，并耗散能量。在颗粒表面摩擦系数相同的情况下，颗粒越小，灾害体被分割得越多，生成颗粒也越多，颗粒表面积总和越大，这就导致了摩擦耗散的能量越多。

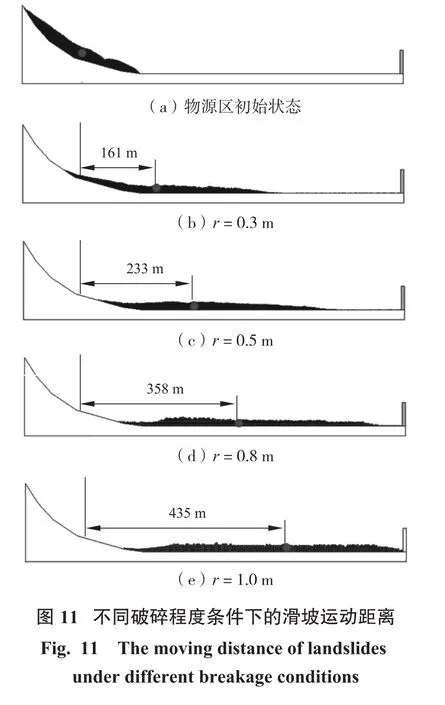
5.2 不同破碎程度灾害体和结构体之间的动力响应

图12中显示的是灾害体颗粒粒径r=0.3 m，结构体到坡脚距离L=0 m时，结构体上所受到的合力的变化。结构体上受到的力分为2个部分，即灾害体对结构体的冲击力（动力载荷）和灾害体施加在结构体上的重力分量（静力载荷）。在实际的滑坡灾害中，由于结构体的破坏主要是缘于灾害体总的合力的作用，动力荷载和静力荷载共同作用并对结构体造成破坏，因此本研究主要考虑合力对结构体造成的影响，并不对2种力进行分解。

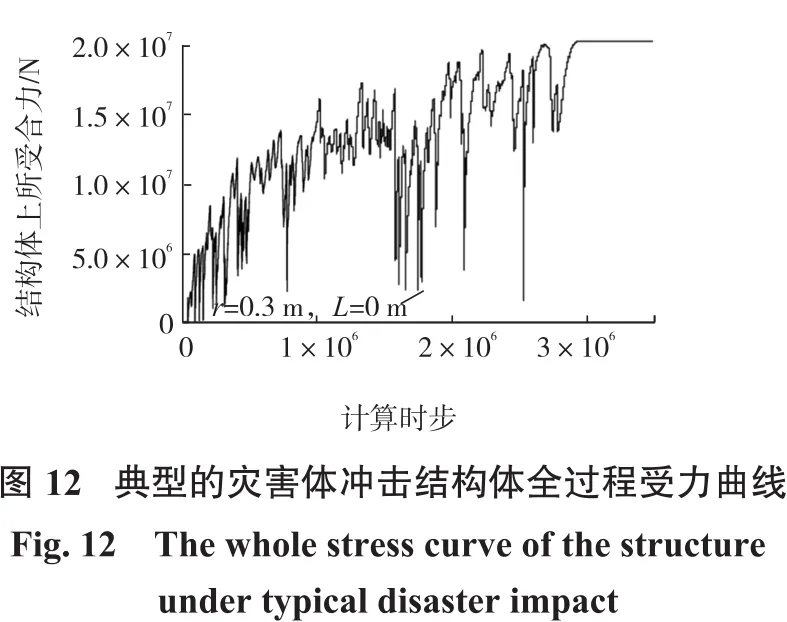
图13中显示的是在不同颗粒粒径条件下，结构体和灾害体之间的距离对结构体所受最大合力的影响。从图中我们可以看出，在任何一组粒径条件下，离灾害体越近的结构体所受的合力的值也越大。我们用二次函数对其进行拟合，发现粒径越大的灾害体（破碎程度较低），其结构体所受合力随距离L的变化程度越明显：当r=1.0 m时，在L=0 m处的最大合力值与L=150 m处的最大合力值之差为5×107N；当r=0.3 m时，在L=0 m处的最大合力值与L=150 m处的最大合力值之差仅仅为1×107N。这是因为随着结构体到坡脚的距离L值增大，灾害体运动过程中的能量损耗不仅仅是颗粒之间的摩擦所造成的，颗粒能量耗散的过程可以分成2个阶段进行：坡面滑动阶段和水平运动阶段。坡面滑动阶段中，灾害体从一定高度滑落到水平阶段并将势能转变为动能，表现在微观方面就是各个颗粒获得了动能，在这个阶段中颗粒开始获得速度，而滑坡灾害体整体能量的耗散主要是通过其颗粒内部摩擦来进行的。水平运动阶段中，各个颗粒获得了较大的动能，并向结构体方向运动。在这个过程中颗粒之间相互挤压碰撞，这是导致滑坡灾害体整体能量耗散的主要原因。由于颗粒越粗，其所组成的灾害体的动能在坡面滑动的过程中能量耗散比较少（颗粒表面积之和小），故而在L=0 m的时候其结构体所受的最大合力值也越大。然而随着结构体到坡脚之间的距离L值增加，大颗粒之间的碰撞、挤压耗散的能量会相对于小颗粒更多，这也导致了从L=0 m到L=150 m之间的大颗粒所组成的灾害体会耗散更多的能量。

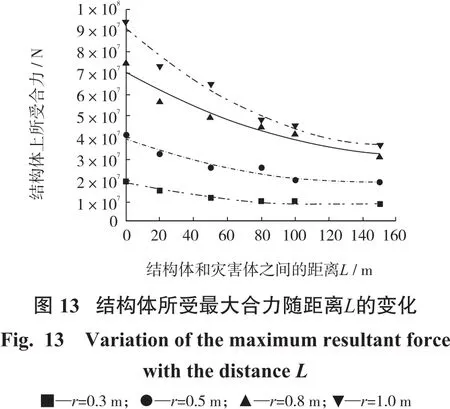
图14中显示的是在不同结构体和灾害体之间的距离L条件下，不同颗粒粒径对结构体所受最大合力的影响。通过图中曲线可以发现不管L的值如何变化，结构体所受最大合力和粒径之间呈线性关系，具体变现：随着粒径地增大，结构体所受最大合力也呈线性关系地逐渐增大，即：F合=kr，其中k表示与L（结构体和灾害体之间的距离）相关的耗能系数。L越大，则k值越小；L越小，则k值越大。

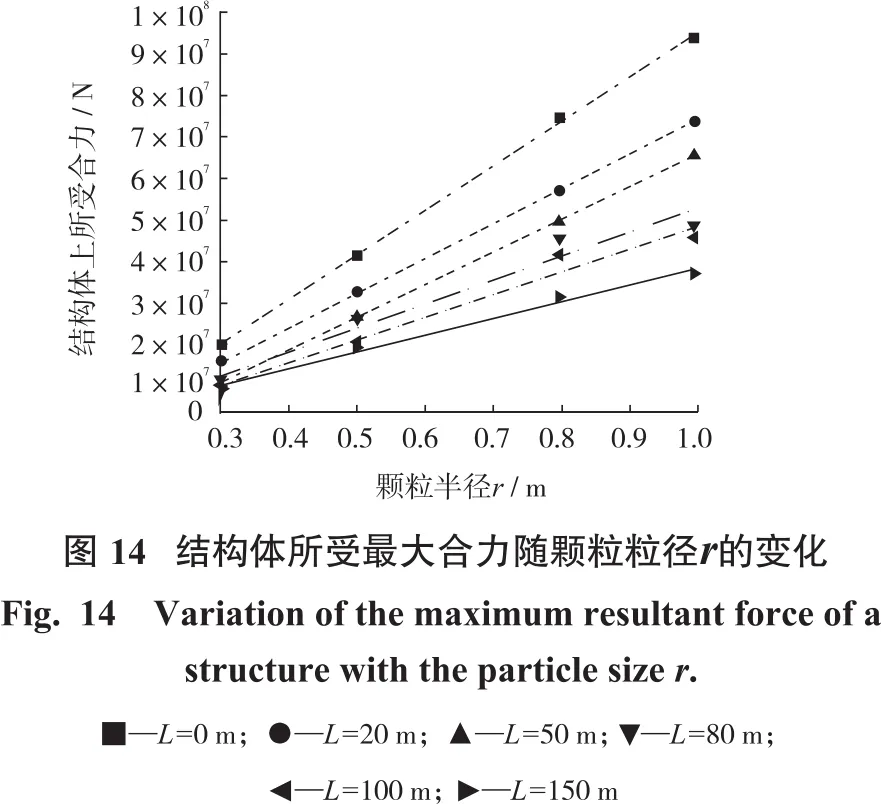
5.3 滑坡灾害条件下的结构体表面应力分布

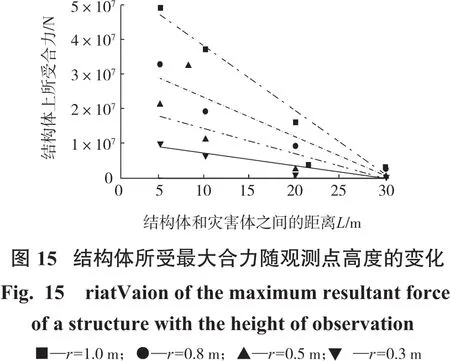
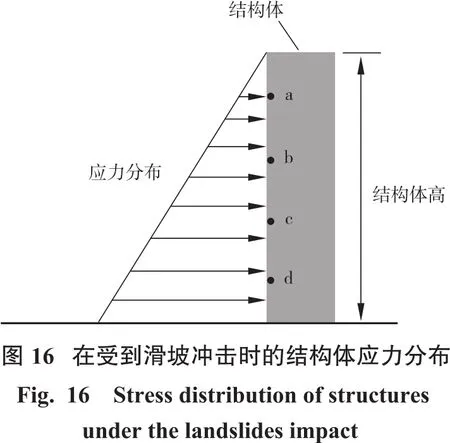
图15中显示的是在结构体所受应力随观测点高度增加而产生的变化。通过图15中的曲线可以发现：在靠近结构体底端的观测点测得的应力值要偏大，而在靠近结构体顶端的观测点测得的应力值偏小；并且随着观测点从低到高，观测点测得的应力值也由高到低分布，其分布规律接近线性分布。并且当粒径r越大的条件下，结构体底部所受应力越大，其分布规律越接近于线性分布。图16中显示的是结构体受到灾害体冲击后，其表面上的应力分布情况。根据示意图上的应力分布，在实际工程设计防护结构时，可以考虑将结构体底部的强度设计得更强一些，而结构体上部的设计可以根据实际情况和经济条件进行适当的优化。

6 结论

（1）滑坡灾害体的运动距离和其破碎程度呈反比；

（2）当灾害体冲击结构体时，结构体上所受的力（包括静力和动力）和结构体与坡脚的距离L有密切联系，具体表现为：F合=kr，其中k表示与L（结构体和灾害体之间的距离）相关的耗能系数；

（3）灾害体破碎程度直接影响了其能量的损耗方式：破碎程度大的灾害体主要在滑坡启动破碎阶段通过颗粒间摩擦来耗损大量能量，破碎程度小的灾害体主要在滑坡运动阶段通过颗粒间碰撞来损耗大量能量；

（4）结构体受到冲击后的表面应力分布满足一个“三角形”，即顶端应力较小，底端应力较大，对于工程上的结构体设计具有一定的指导意义。由于本研究中的模型是建立在二维数值模拟平台中，对实际问题进行了部分简化，特别是在模型建立这个方面，所以为了得到更精确的结果，在后续的工作中应根据具体的地质条件建立三维模型并加以研究。