煤层气的温度-压力-吸附方程的数学分析和诠释
李 东 郝静远
(西安思源学院,能源及化工大数据应用教学研究中心,陕西 710038)
1 引言
为了探讨温度、压力、煤质对煤吸附量的综合影响,研究人员都做系列等温吸附实验,并常用兰格缪尔等温吸附方程进行处理。通过系列等温吸附实验数据的对比分析,学者研究高温高压下不同煤的吸附行为,不同煤种不同温度的兰格缪尔吸附常数,煤样的解吸。也有学者研究多元气体的等温吸附、镜质组最大反射率与兰格缪尔吸附常数之间的关系、实测值与理论值的差别以及煤岩与页岩系列等温吸附的差别。但是众所周知,地层中深度的变化会引起规律性温度变化(地温梯度)和压力变化(地压梯度)。但自兰格缪尔发表其等温吸附方程一百年来,从未有将温度、压力、和吸附体积有机地联系起来的数学方程。本文希望建立温度、压力、吸附介质(自变量)与吸附量(应变量)有机地联系起来函数关系的数学方程。并用其他学者的系列等温吸附实验数据对该温度-压力-吸附方程进行验证。最后通过对这个方程的数学偏导和全微分定量地讨论这些自变量与应变量相互影响。
2 吸附实验数据来源
所有吸附实验数据,都以鄂尔多斯盆地东部4种主要煤层(长焰煤YP、肥煤NY、瘦煤MZQ、和贫煤XS)为测试对象,并模拟煤层埋深在1000~3000m之间为温度压力条件,均取自国内学者的系列等温吸附实验数据。
固体对气体的吸附量是温度和气体压力的函数。在恒温下,反映吸附量与平衡压力之间关系的曲线称为吸附等温线。惯用的Langmuir等温吸附方程就是其中著名的一个方程。 其表现形式为:
(1)
式中:V是吸附量,cm3g-1,a=VL是兰氏体积,cm3g-1;P是压力,MPa;b=1/PL是兰氏方程参数,MPa-1。
表1列出四种煤样进行系列等温吸附实验的兰氏体积和兰氏压力参数。
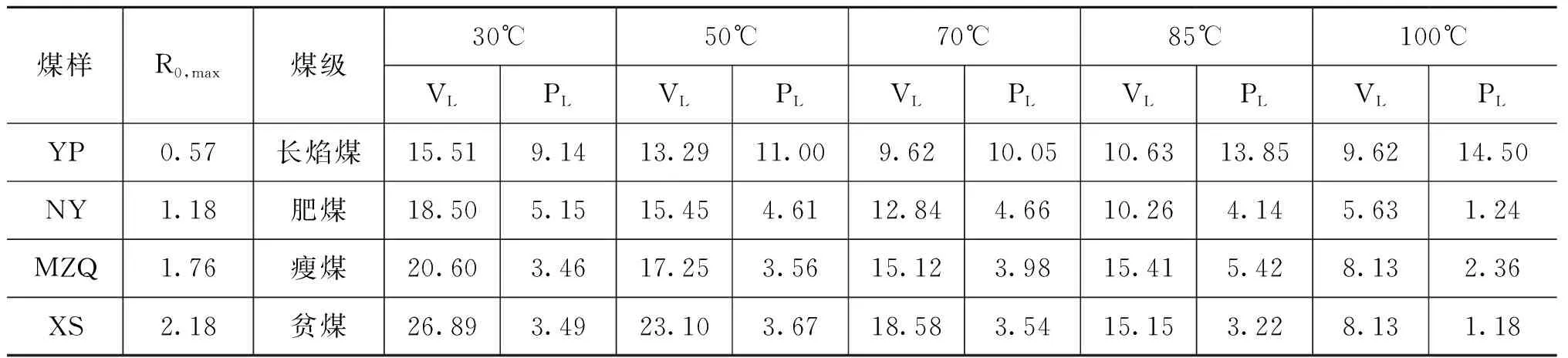
表1 吸附实验煤样资料和参数
3 温度-压力-吸附方程(TPAE)形式及参数计算
3.1 方程形式
在讨论多孔无机膜气体分离的机理时,一般都包含努尔森(Knudsen)扩散、表面扩散、多层扩散与毛细管冷凝、和分子筛效应。通过计算无机膜气体分离的努尔森(Knudsen)扩散和表面扩散,Hwang和Kammermeyer得到气体渗透率(Gas permeability)与温度的数学方程。为了解释温度-压力-气体渗透率的关系,Li和Hwang采用Freundlich 等温吸附方程表示局部吸附复盖(fractional adsorption coverage)得温度-压力-气体渗透率的数学方程。
当比较煤层气吸附与无机膜气体分离时,可以看到至少有以下五点相似:
(1)两者都是物理过程,都未发生组分的化学变化;
(2)都与温度、压力、接触介质有关;
(3)在推导气体渗透率中用到等温吸附方程;
(4)在推导气体渗透率中假设气相和吸附相已经存在热力学平衡,因此吸附分子在吸附介质表面的迁移是表面扩散;和
(5)如果将温度-压力-气体渗透率的气体渗透率改为单位气体吸附量V(m3/t),并将压力单位修正为煤层气吸附测定压力单位兆帕,得温度-压力-吸附方程(Temperature-Pressure-Adsorption Equation,TPAE),并表现为
(2)
式中:V是吸附量,m3/T;A是对于一个固定的多孔介质的微孔几何形体常数(如孔的形状等),无量纲;B是吸附流量系数,都与吸附站点区域相关(如吸附介质的孔隙率、吸附比表面积等),无量纲;M是分子量,甲烷的分子量为16;T是热力学温度,K;P是压力,兆帕;Δ是在吸附质流中的一个吸附分子的最低势能和活化能之间的能量差(显示温度的影响),K;β是类似于Freundlich 吸附等温线方程中的压力参数(显示压力的影响),无量纲。
3.2 参数计算
因为吸附数据是系列等温吸附实验的兰氏参数,表1。所以验证首先是建立回归样本,后回归计算TPAE参数。将这些兰氏参数代入Langmuir等温吸附方程1,计算出一系列测试温度下不同压力时的吸附体积作为回归样本群。再根据这些回归样本群(也称为变温和变压数据集)按TPAE用非线性回归计算确定四个参数A、B、Δ和β。四种煤的TPAE的回归计算结果列于表2。

表2 根据表1兰氏体积和兰氏方程参数回归得TPAE参数
4 结果与讨论
4.1 TPAE的适用性
将表2的参数代回TPAE计算出与回归样本群一一对应的温度压力下的吸附体积,计为计算样本群。根据方程3算回归样本与计算样本的相对偏差。表3列出四种煤样的相对偏差。

(3)

表3 四种煤样的平均相对偏差范围
表3中四种煤样的平均相对偏差值都较小(YP长焰煤样的8.73%、NY肥煤样的12.6%、MZQ瘦煤样的11.7%、XS贫煤样的12.6%)说明TPAE适用于处理系列等温吸附实验数据。换句话说,TPAE能够取代系列等温兰氏方程组。
4.2 TPAE的可视性
因为TPAE是包含温度与压力二维变量的方程。图1中显示长焰煤YP和贫煤XS的TPAE曲面与回归样本。图1上的点则代表长焰煤YP和贫煤XS的回归样本。从图1中可以看出TPAE曲面与回归样本吻合很好。这进一步说明TPAE适用于处理系列等温吸附实验数据。

图1 鄂尔多斯盆地东部的长焰煤和贫煤吸附实验结果比较
4.3 TPAE的偏导数和全微分
如果A值相对较小而被忽略,则TPAE简化为:
(4)
若V=f(T,P)的各一阶偏导数都存在且连续,则
(5)
式中
(5-1)
(5-2)
方程5是变温度和变压力对吸附量变化的共同影响的数学表达式,也是方程2的全微分。基于以上方程组还可以做以下数学推论:
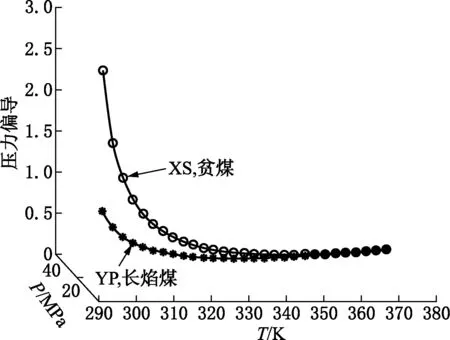
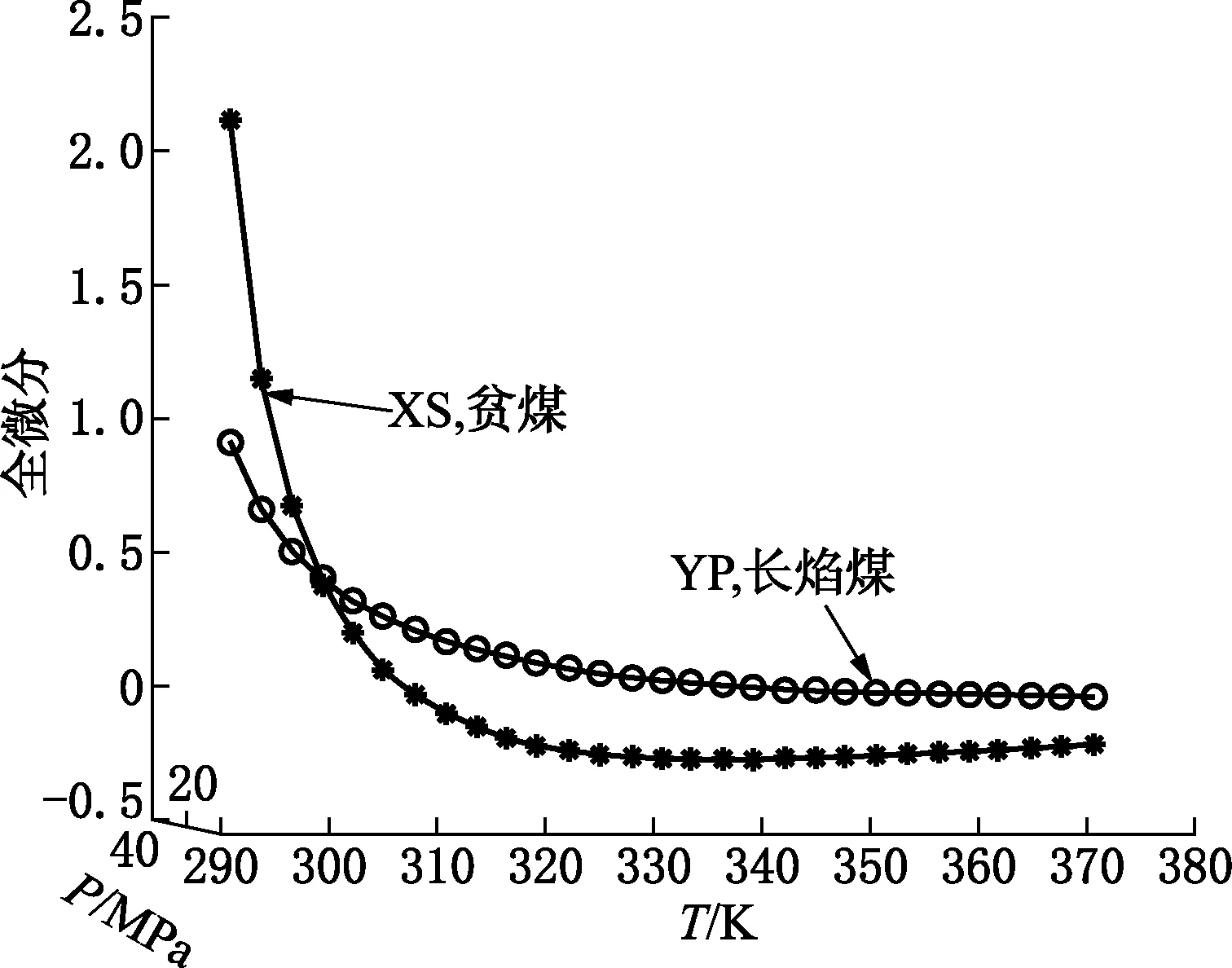
根据方程5-1,等压升温条件下,吸附量的变化方向取决于Δ与T的相对大小。如果Δ>T,方程的右边小于零,等压条件下吸附量的变化受温度变化的负影响。如果Δ 根据方程5-2的右边永远不会变为负号,所以在等温条件下,吸附压力对煤的吸附能力永远起着正影响; 如果方程组中涉及的四个TPAE参数已知,并且选定温度的变化量(从T1到T2)和压力的变化量(从P1到P2),那么吸附量对温度偏导、吸附量对压力偏导、和吸附量对温度和压力的全微分是可以精确计算的。在计算中用到的T、P、dT和dP为: (6-1) (6-2) dT=T2-T1 (6-3) dP=P2-P1 (6-4) Vi+1=Vi+dVi+1 (6-5) 图2表现长焰煤YP和贫煤XS在恒压条件下吸附量对温度求偏导。在恒压条件下吸附量对温度求偏导是负值,即小于零,并且压力的影响仍然存在。压力对吸附量的影响并不会因为压力的衡定而消失。 图2 长焰煤YP和贫煤XS在恒压条件下的温度偏导 图3表现长焰煤YP和贫煤XS在恒温条件下吸附量对压力求偏导。在恒温条件下吸附量对压力求偏导是正值,即大于零。并且温度的影响仍然存在。温度对吸附量的影响并不会因为温度的衡定而消失。 图3 长焰煤YP和贫煤XS在恒温条件下的压力偏导 如果假设地质勘探结果是埋深增加100m,地温增加3℃导致吸附量减少、地压增加1MPa导致吸附量增加,计算结果可以比较埋深每增加100m究竟是温度偏导贡献大些,还是压力偏导贡献大些;这就是全微分计算的用途。四种煤的全微分都出现一个拐点,其特征是全微分由正值变为负值;图4表现长焰煤YP和贫煤XS的全微分。 图4 长焰煤YP和贫煤XS在变温变压下的全微分 图5 长焰煤YP和贫煤XS在变温变压下的吸附量 因为四种煤的全微分出现一个由正值变为负值拐点,那么四种煤的吸附量会在出现拐点的温度和压力处出现一个极值,而且是一个极大值。如表4所示,随着煤的变质程度的提高,出现极大值时的温度和压力会降低。换句话说,对于高变质程度的煤,因为其出现拐点的温度和压力都较低而比较容易被观察到。对于低变质程度的煤,因为其出现拐点的温度和压力都较高而比较不容易被观察到。图5表现长焰煤YP和贫煤XS的吸附量。 表4 四种煤出现拐点,即吸附量出现极大值的温度和压力 在数学形式上,TPAE首次将温度-压力-吸附煤质这些自变量与吸附体积应变量以一个数学方程直接联系起来。 用其他学者的系列等温吸附实验的兰氏体积和兰氏压力数据建立煤层气吸附的回归样本群,回归计算得到该种煤TPAE四个参数。根据回归得到的TPAE四个参数可以生成与回归样本群相对应的计算样本群。 三种判定方法(最小相对偏差、最大相对偏差、和平均相对偏差综合评价,部分具体温度和压力条件下的回归样本值和计算样本值之间的相对偏差,和TPAE曲面与回归样本吻合程度)都说明TPAE可以处理系列等温吸附实验数据取代系列等温兰氏方程组。 TPAE的数学推导以及数据计算显示:恒温变压条件下,煤层气吸附量随压力增大而增大,且不同压力区间其增加的幅度是不同的;恒压变温条件下,煤的吸附量总体上是随温度的增加而减少且温度区间不同吸附量减少的程度也不同。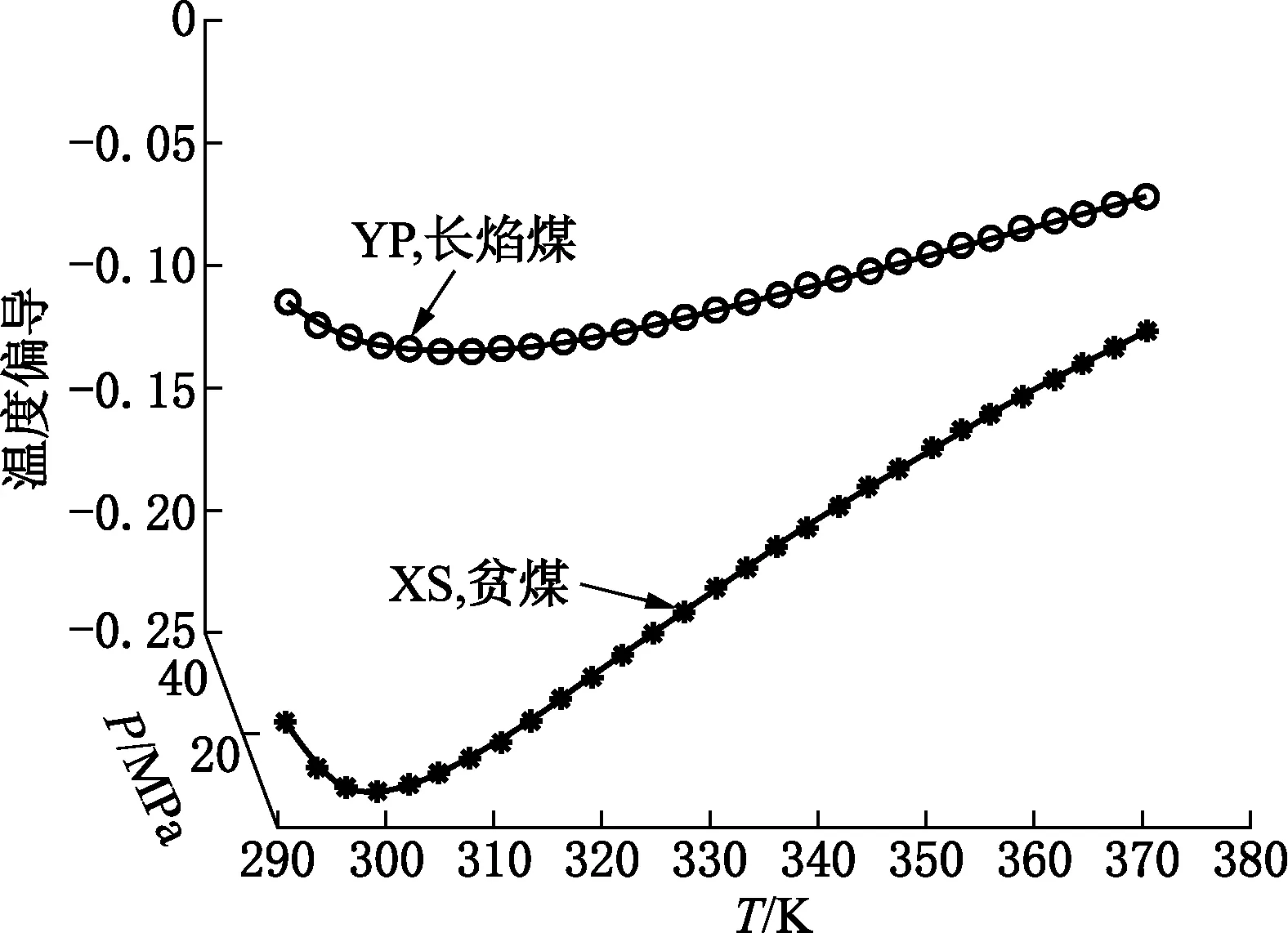


5 结论

