对一道定值问题的探究、拓展及应用

北京 赵 毅 刘 刚

解析几何是一门用代数方法研究几何问题的学科，是高中数学重要内容之一，在高考中占有重要地位．从各类考试看，重点考查圆锥曲线的定义、标准方程、几何性质以及直线和圆锥曲线的位置关系，其中定值、定点问题是圆锥曲线中一类重要题型，它揭示了圆锥曲线所固有的某些几何或代数性质，是历来考试中的热点问题．下面以一道定值问题为例，剖析其解法，并运用特殊到一般的方法，挖掘其一般规律；同时运用类比的思想，尝试在其他圆锥曲线中进行推广与拓展，供大家参考．

一、试题

(2017·绵阳市高三第三次诊断考试)已知点E(-2,0)，点P是圆F:(x-2)2+y2=36上任意一点，线段EP的垂直平分线交FP于点M，点M的轨迹记为曲线C．

(Ⅰ)求曲线C的方程；

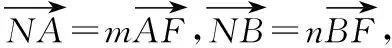
试题以圆为背景考查了椭圆的定义、直线与椭圆的位置关系以及定值问题，考查了坐标法的运用．试题解法灵活，内涵丰富，是一道具有研究性学习价值的好题．

二、解法探究

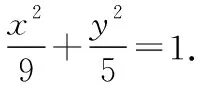
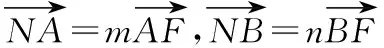
解法1：由题意知F(2,0)，若直线AB恰好过原点，

则A(-3,0)，B(3,0)，N(0,0)，

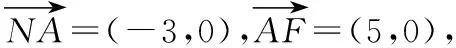
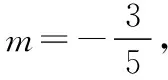
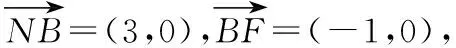
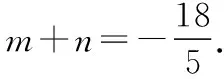
若直线AB不过原点，

设直线AB:x=ty+2(t≠0)，A(ty1+2,y1)，

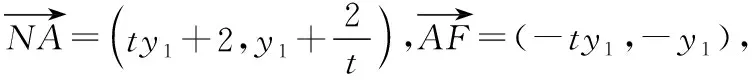
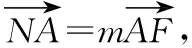
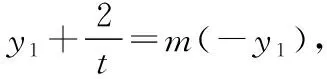
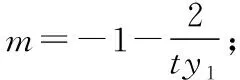
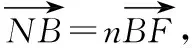
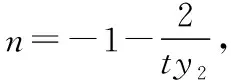
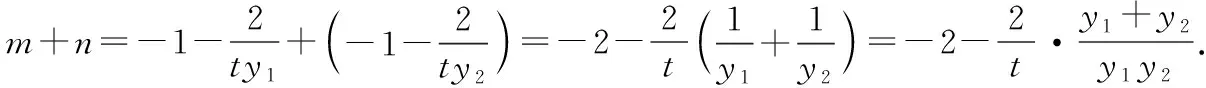
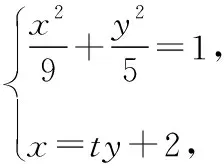
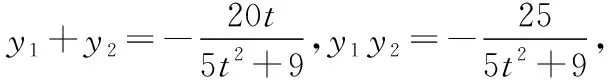
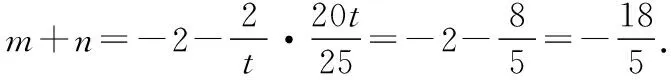
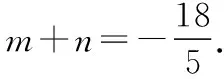
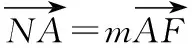
解法2:由题意知F(2,0)，m≠-1，n≠-1，

设A(x1,y1)，B(x2,y2)，N(0,y0)，

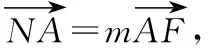
得(x1,y1-y0)=m(2-x1,-y1)，

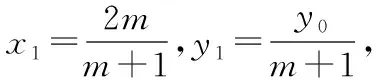
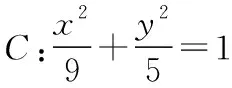
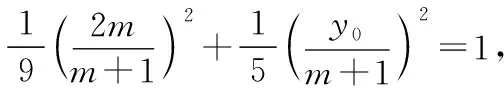
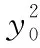
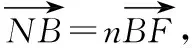
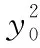
由此可得m，n是关于x的一元二次方程

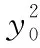
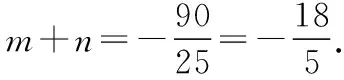
三、拓展

经过对本题的一般化探究，可以得到下面的一组定值性质．

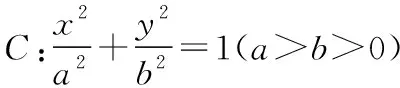
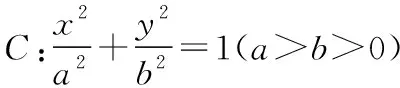
证明：由题意知，m≠-1，n≠-1，

设A(x1,y1)，B(x2,y2)，N(0,y0)，

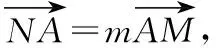
得(x1,y1-y0)=m(x0-x1,-y1)，

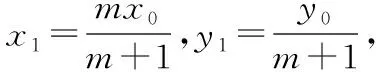
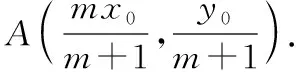
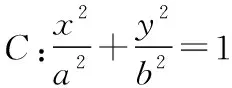
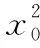
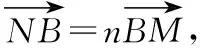
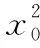
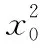
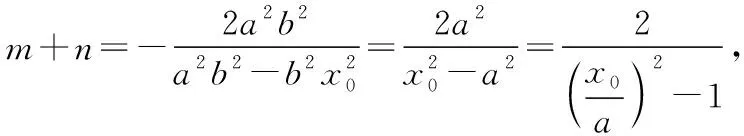
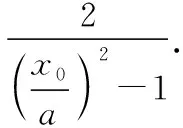
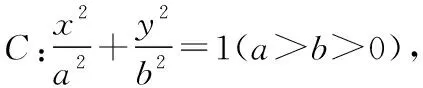
证明：由题意知，m≠-1，n≠-1，

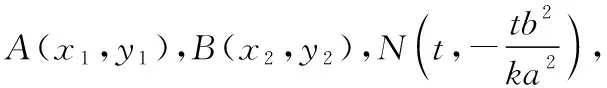
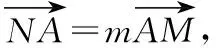
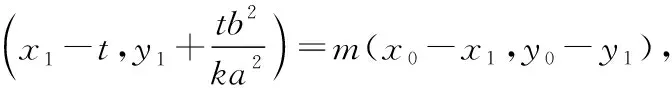
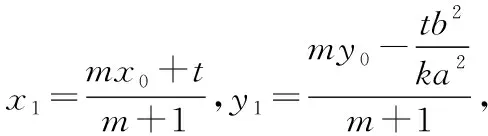
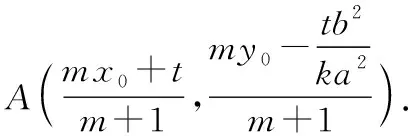
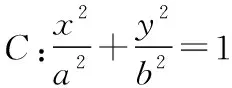
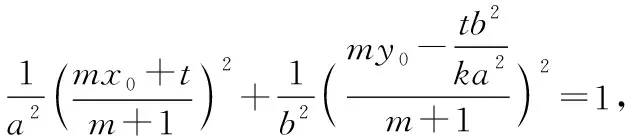
整理得

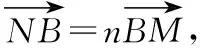
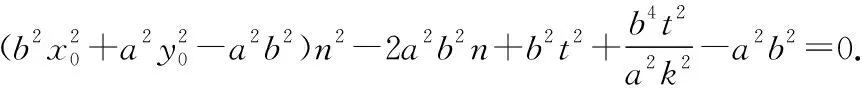
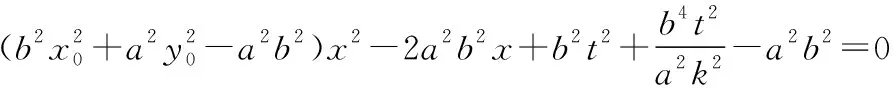
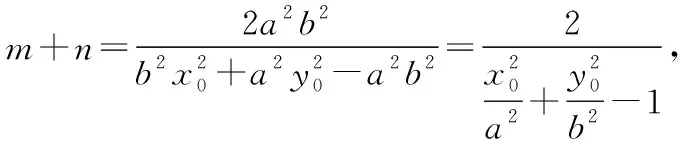
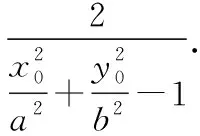
由椭圆类比到双曲线、抛物线，可得另外两条性质．

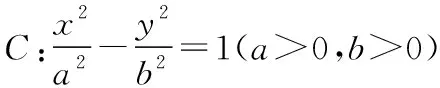
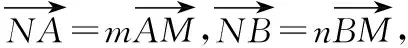
证明:由题意知，m≠-1，n≠-1，

设A(x1,y1)，B(x2,y2)，N(0,y0)，

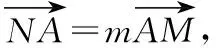
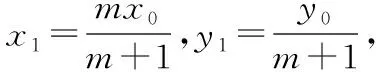
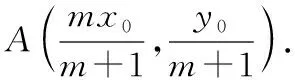
因为A点在抛物线C:y2=2px上，

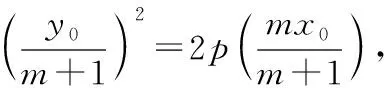
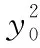
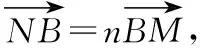
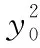
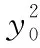
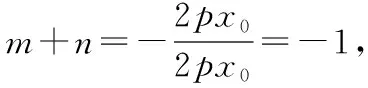
故m+n为定值-1．

四、应用

【例1】已知线段AB的两个端点A，B分别在x轴，y轴上滑动，|AB|=3，点M是线段AB上一点，且|AM|=1，点M随线段AB的滑动而运动．

(Ⅰ)求动点M的轨迹E的方程；

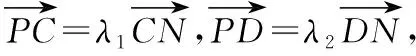
解：(Ⅰ)设A(m,0)，B(0,n)，M(x,y)，

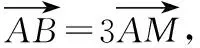
即(-m,n)=3(x-m,y)，

因为|AB|=3，所以m2+n2=9，

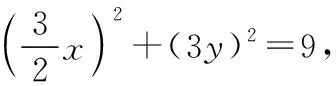
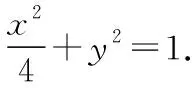
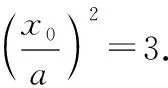
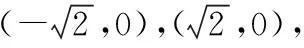
(Ⅰ)求E的方程；

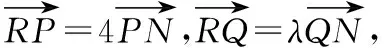
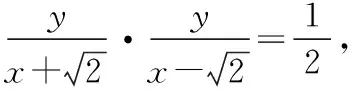
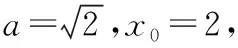
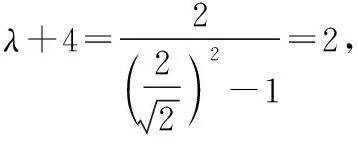
【例3】已知抛物线C:y2=2px(p>0)的焦点到准线的距离为4.

(Ⅰ)求抛物线C的方程；

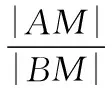
解：(Ⅰ)由已知，得p=4，所以抛物线C的方程为y2=8x．