对一道斜率定值问题的探究

河北 赵伟娜

解析几何中的定值问题是高考中经常考查的一类题型，如果能发现规律，利用规律总结思想方法，积累运算技巧，就可以提高运算效率，加快解题速度.下面就结合一道具体的例题展开探究.

( )

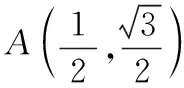
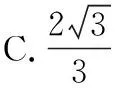
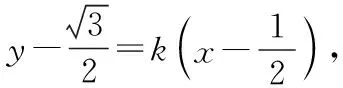
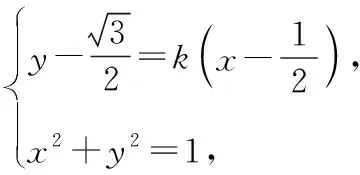
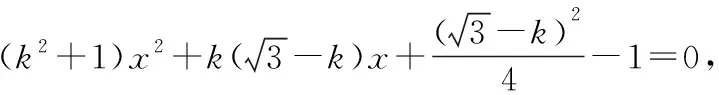
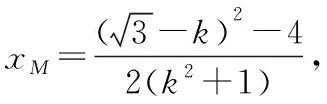
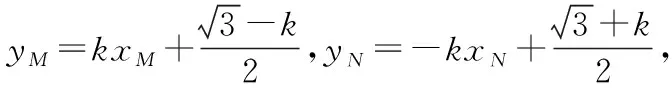
则yM-yN=k(xM+xN)-k，

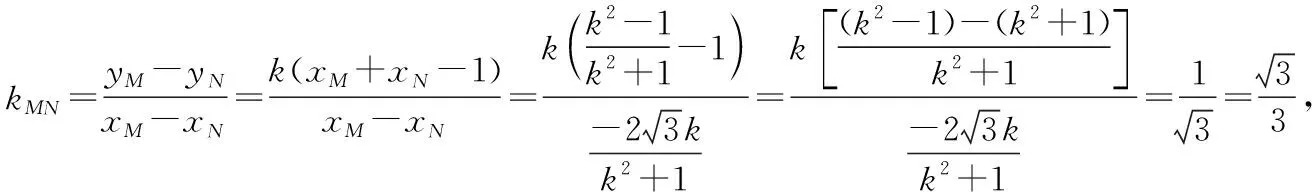
根据此题，我们发现如果将定点改变，将曲线方程进行推广，思路方法和运算方法仍然适用，并且结论也有一定的规律可循.

推广一：已知点A(x0,y0)是圆C：x2+y2=r2上的点，过点A且与圆C相交的直线AM，AN(都存在斜率)的倾斜角互补，则直线MN的斜率为________.

【解析】设AM的方程为y-y0=k(x-x0)，

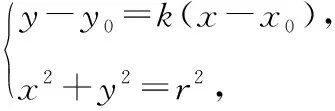
(k2+1)x2+2k(y0-kx0)x+(y0-kx0)2-r2=0，

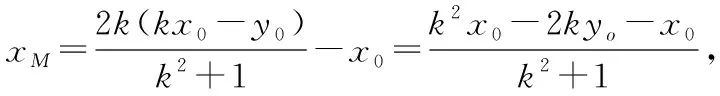
而yM=kxM+y0-kx0，yN=-kxN+y0+kx0，

则yM-yN=k(xM+xN)-2kx0，

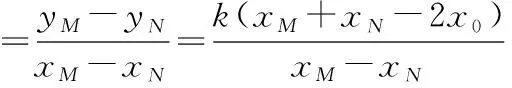
显然上题是此推广一的一种情况.

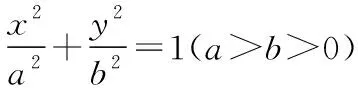
【解析】设AM的方程为y-y0=k(x-x0)，

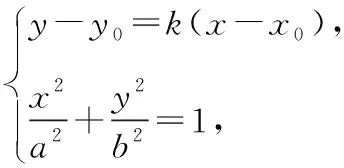
(a2k2+b2)x2+2a2k(y0-kx0)x+a2(y0-kx0)2-a2b2=0，

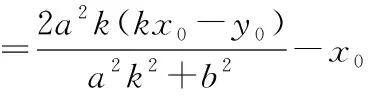
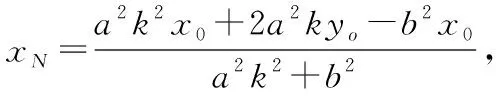
而yM=kxM+y0-kx0，yN=-kxN+y0+kx0，

则yM-yN=k(xM+xN)-2kx0，

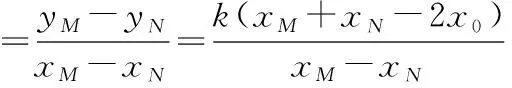
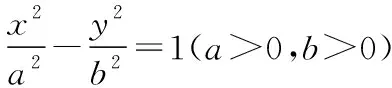
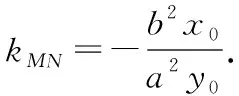
推广四：已知点A(x0,y0)是抛物线y2=2px(p>0)上的点，过点A且与抛物线相交的直线AM，AN(都存在斜率)的倾斜角互补，则直线MN的斜率为________.

【解析】设AM的方程为y-y0=k(x-x0)，

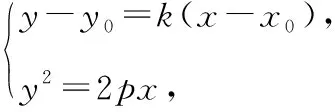
ky2-2py-2pkx0+2py0=0，

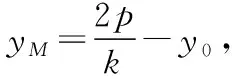
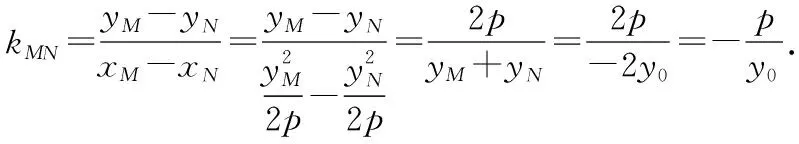
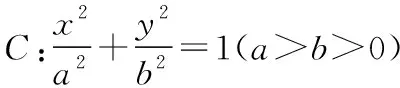
(1)求椭圆C的标准方程；

(2)P，Q是椭圆C上的两个动点，如果直线AP的倾斜角与AQ的倾斜角互补，证明：直线PQ定向(即该直线的斜率为定值).

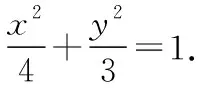
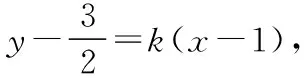
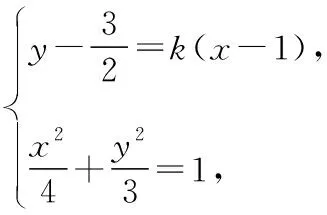
(4k2+3)x2-(8k2-12k)x+4k2-12k-3=0，

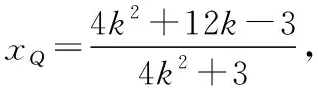
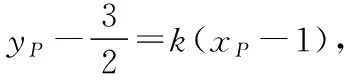
则yP-yQ=k(xP+xQ-2)，

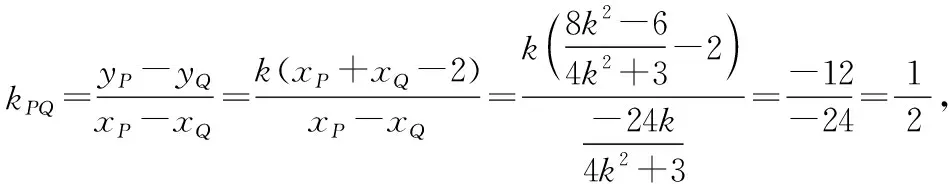
本文从一道小题出发进行探究，得到了此类问题的解题方法，由圆到椭圆到双曲线到抛物线都有这种解法和结论，如果是选择填空题可以直接代入结论得到结果，解答题就可按照此方法推理证明.