基于FPGA的GNSS外辐射源合成孔径雷达成像算法设计与实现
,,,,
(湖北大学 计算机与信息工程学院,武汉 430062)
0 引言
合成孔径雷达具有全天时、全天候、远作用距离和高分辨等特点,在战场侦察、空间探测和民用遥感等领域具有重要的应用价值。双基合成孔径雷达由于其发射机与接收机在地理位置上分离,因此具有安全性好等技术优势。外辐射源合成孔径雷达是一类采用第三方装置作为发射机的被动式雷达,是传统双基合成孔径雷达的一个分支。
在GNSS外辐射源雷达系统中,发射机为GNSS卫星,可以是美国的GPS,俄罗斯的GLONASS,欧洲的Galileo或者是中国的北斗。而接收机可以部署在飞机上,汽车上,或者直接固定在地面,地理位置十分灵活。该雷达系统拥有安全性强,观察角度丰富,系统稳定性好,部署成本低等技术优势,已成为雷达业界的研究热点[1-3]。
合成孔径雷达成像算法主要分为时域算法和频域算法。时域算法准确性高,且运算复杂度不受雷达系统几何结构的变化而改变。缺点表现在运算量较大,尤其在大场景情况下将十分严重。其代表性算法为Back-projection(BP)算法。频域算法效率高,然而其数学建模与实现细节随雷达几何结构变换而改变,且准确性较时域算法有一定差距。其代表性算法有Range-Doppler (RD), Chirp Scaling (CS)等。
FPGA由于并行处理和编程灵活等特点,已在合成孔径雷达成像中展现出广泛的应用。西安电子科技大学等相关团队纷纷开展了实用FPGA进行合成孔径雷达成像的研究[4-7],并取得了良好的实用效果。
GNSS外辐射源合成孔径雷达在雷达作用距离、分辨能力、双基同步、理论成像方面均已有广泛的研究和成果。然而,在实用化的研究方面存在空白。
本文采用FPGA对外辐射源合成孔径雷达成像进行处理。本文第一节介绍了外辐射源合成孔径雷达成像算法的理论依据;第二节讨论了采用FPGA对该算法的设计与实现;第三节给出了实测数据的成像结果与分析,最后对本文进行了总结。
1 外辐射源合成孔径雷达成像算法
1.1 外辐射源合成孔径雷达信号模型
图1给出了外辐射源合成孔径雷达系统几何示意图。GNSS卫星作为发射机,沿预定轨道运行,轨道高度距地球表面20 000 km, GNSS卫星不间断的向地球表面发射GNSS信号。雷达接收机搭载在无人机上,无人机距地面1 000 m,沿直线匀速飞行。雷达接收天线照射方向与无人机飞行方向垂直。
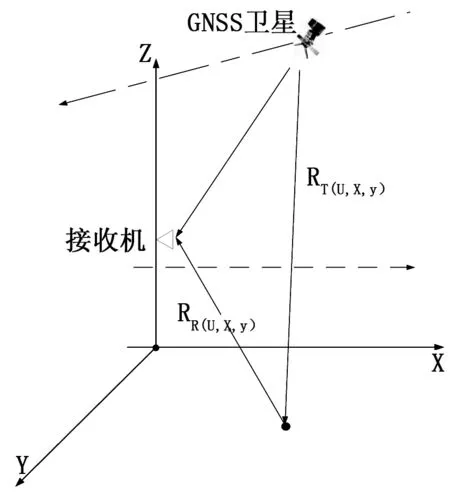
图1 具有GNSS和固定接收机的SS-BSAR的几何图形
雷达接收机上配备两副天线,GNSS直达波接收天线和雷达波接收天线。GNSS直达波接收天线直接接收来自GNSS发射的信号,该信号用于实现GNSS卫星与雷达接收机之间的同步。
假设GNSS卫星坐标表示为(xt,yt,zt), 雷达接收机坐标为(xr,yr,zr), 目标区域在X-Y平面内。点目标位于(x,y,0),正交解调后从该区域反射的接收信号可以表示为:
s(t,μ)=
P[t-τ2(u,x,y)]Dp[t-τ2(u,x,y)]e[j(wd2(u,x,y)t+φ2(u,x,y))]+
j×CA[t-τ2(u,x,y)]Dca[t-τ2(u,x,y)]e[-j(wd2(u,x,y)t+φ2(u,x,y))]
(1)
其中:
(2)
(3)
(4)
φ2(u,x,y)=φe2(u,x,y)+φp2(u,x,y)
(5)
ωd2(u,x,y)=Δφ2(u,x,y)/2π
(6)
(7)
P[]是P码的包络,CA[]是CA码的包络,DP[]是P码上携带的导航电文,Dca[]是CA码上携带的导航电文,τ2是雷达波在传播过程中产生的延迟,RR是接收机到目标范围,RT是发射机到目标范围,φ2和ωd2是雷达波接收信号的相位和多普勒,φe2和φp2是由波传播引起的相位噪声和相位。
1.2 外辐射源合成孔径雷达成像BP算法
外辐射源合成孔径雷达成像BP算法主要包括两个步骤:距离压缩和后向投影。
1.2.1 距离压缩
外辐射源合成孔径雷达距离压缩是将雷达波天线接收信号与参考信号在每个慢时间轴上实现距离方向上脉冲压缩。雷达波天线接收信号由式(2.1)所示,参考信号为根据预处理后获得的GNSS直达波参数重构产生的信号。由于外辐射源合成孔径雷达预处理不在本文研究范围内容,因此其相关内容不再赘述,相关内容详见参考文献[3]。根据预处理获得GNSS直达波参数,重建产生的参考信号可以表示为:
Ssync(tn,u)=P[tn-τ(u)]Dp[tn-τ(u)]×
e(jwor(u)tn)e(j[Φ(u)-Φp(u)-Φn(u)])
(8)
(9)
式中,τ(u,x,y)是GNSS直达波接收信号的时间延迟。wor(u)是根据GNSS卫星官方轨道坐标和雷达接收机坐标计算获得的角速度。φ(u)是GNSS直达波接收信号进行跟踪后获得的相位信息。φp是根据GNSS卫星官方轨道坐标和雷达接收机坐标计算获得的相位信息,φn是GNSS直达波接收信号中提取的导航电文。从公式(2.7)可以看出,本地生成的参考信号以P码为包络,时间信息为GNSS直达波接收信号延迟,频率为根据GNSS卫星坐标与雷达接收机位置计算或的多普勒历史,相位为GNSS直达波接收信号跟踪获得的相位信息与名义相位信息以及导航电文引入的相位信息的差。
式(2.7)也可以表示为:
Ssync(tn,u)=P[tn-τ(u,x,y)]D[tn-τ(u,x,y)]
e(jwor(u,x,y)tn)ej[Φe(u,x,y)]
(10)
其中:
Φe(u,x,y)=Φ(u)-Φp(u)-Φn(u)
(11)
因此,结合式(1)和式(11),外辐射源合成孔径雷达距离压缩可以表示为:
Src(t,u)=s(t,u,x,y)○*Ssync(tn,u)=
CFp[t-(τ2(u,x,y)-τ(u))]×
e[j(φp2(u,x,y)+φe2(u,x,y)-φe(u,x,y)+(τ2(u,x,y)-τ(u))π)]+
j×P[tn-τ(t)]○*[t-(τ2(u,x,y)-τ(u))]×
e[j(φp2(u,x,y)+φe2(u,x,y)-φe(u,x,y)+(τ2(u,x,y)-τ(u))π)]
(12)
式(12)中,由于C / A码和P码的互相关为零,因此式(12)中第二项为零,只保留第一项。式(12)可以表示为:
Src(t,u)=CFp[t-(τ2(u,x,y)-τ(u))]
(13)
式(13)中包括距离压缩后信号的包络以及相位,包括的幅度为相关函数CFp[]。相位信息包括三部分:
其中第一项φp2(u,x,y)是雷达信号在目标(x,y,0)处产生的相位,用于成像过程中的方位向压缩。
第二项φe2(u,x,y)-φe(u,x,y)是由GNSS直达波接收信号和雷达波接收信号之间的接收机噪声,气氛伪影等引起的相位误差的差异。由于在本雷达系统中,两通道结构特性一致,因此该项近似为零。
第三项(τ2(u,x,y)-τ(u))π是由导航消息相移引起的两通道之间的相位差。该值取决于雷达波传输路径和直达波传输路径的差,如果距离差在一个导航信息周期内,则该值为零。由于导航消息间隔为20毫秒,这对应于Dcritical=c×20 ms=6 000 km,这大大超过雷达波与直达波传输路径的差值,因此,该项为零。
依据上述分析,距离压缩信号可以简化为:
Src(t,u)=CFp[t-(τ2(u,x,y)-τ(u))]×
e[jφp2(u,x,y)]
(14)
式(14)表明,通过距离向压缩,信号的相位信息只包含了雷达波信号传输引入的相位。
1.2.2 后向投影
距离压缩之后,将进行后向投影运算,具体步骤如下。
1)对所有目标的快速时间信号进行Sinc插值操作:
Indinterp=[τ2(u,x,y)-τ(u)]×fADC
(15)
其中:fADC是ADC的采样频率。组合方程(14)和(15),内插后方位向实践u中来自目标(x,y,0)的压缩信号可以表示为:
Srci(t,u)=CFp[t-(τ2(u,x,y))]×e[jφp2(u,x,y)]
(16)
2)方位向匹配滤波。方位向匹配滤波器表达式为:
(17)
其中:fc是卫星信号载波频率,Rcenter是合成孔径中心和场景中心之间的斜距。
因此,引入式(16)和(17),方位向压缩可以表示为:
(18)
式(18)可以看出,方位向压缩后,位于(x,y,0)的点目标聚焦。
2 基于FPGA的SAR成像算法实现
本文以DE1 SOC为硬件平台,在QuartusII14.0开发环境下,用Verilog HDL语言设计实现了外辐射源合成孔径雷达成像算法,其总体框架如图2。
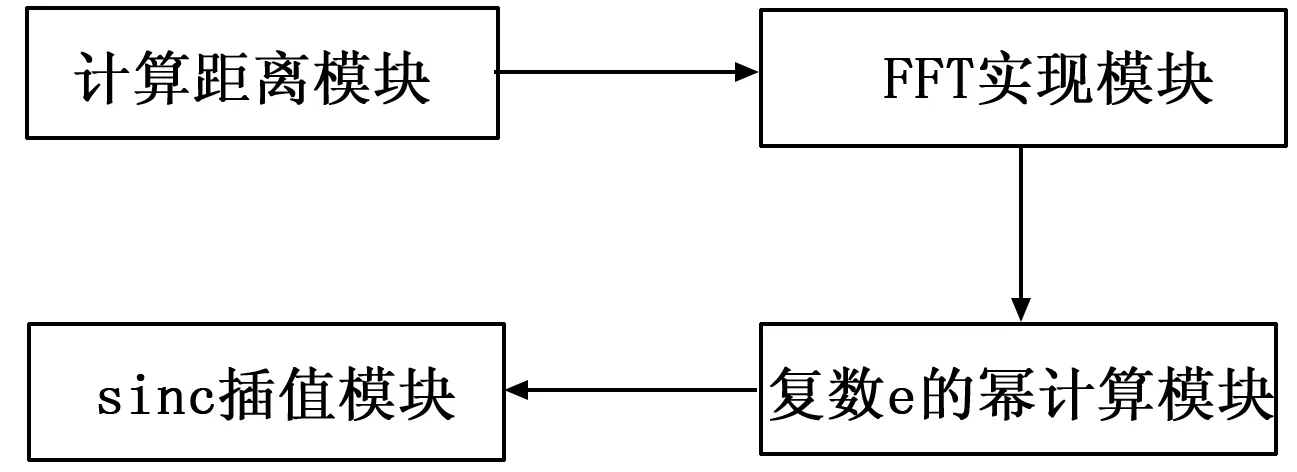
图2 外辐射源合成孔径雷达FPGA实现总体框图
该成像算法流程包括四个模块:距离计算法模块、FFT实现模块、复数e的幂计算模块一级Sinc插值模块。其主要模块为计算距离模块以及FFT实现模块,下文将详细介绍这两个模块。
2.1 计算距离模块

图3 计算距离模块
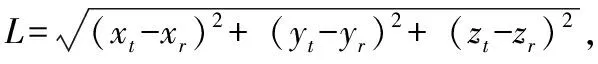
2.2 FFT实现模块
在本文提出的成像算法中,FFT运算模块实现时域与频域之间的转换,其具体实现结构包含以下部分:PLL分频模块,数据存储模块,控制模块, FFT 计算模块等。FFT模块流程如图4所示。
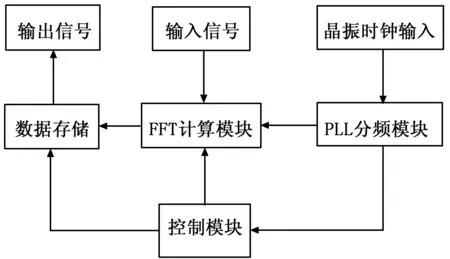
图4 FFT模块实现流程图
其中PLL分频模块提供不同频率的时钟,控制模块控制FFT计算模块按照正确的时序进行读取数据操作和数据输出操作,数据存储模块保存输出的数据供后续使用。
2.2.1 PLL分频模块
时钟的分频由锁相环技术实现。通过更改锁相环电路的比例参数,电路能够将输入的时钟信号分频或倍频从而得到所需频率。为了保证时钟信号稳定可靠,本文采用官方提供的PLL功能IP核。
2.2.2 控制模块
控制模块包括FFT控制模块和数据存储控制模块,控制模块的作用是控制FFT算法模块和存储模块进行数据处理和存储。
数据存储控制模块使得FFT输出与数据存储保持时间同步,能够进行正常的数据读取。FFT控制模块是对FFT计算模块进行一定的时序约束,使其按照所需的时序进行工作。
2.2.3 FFT计算模块
FFT计算模块包括FFT IP核、FFT赋值校正模块、异步时钟存储模块,时钟信号由外界提供。
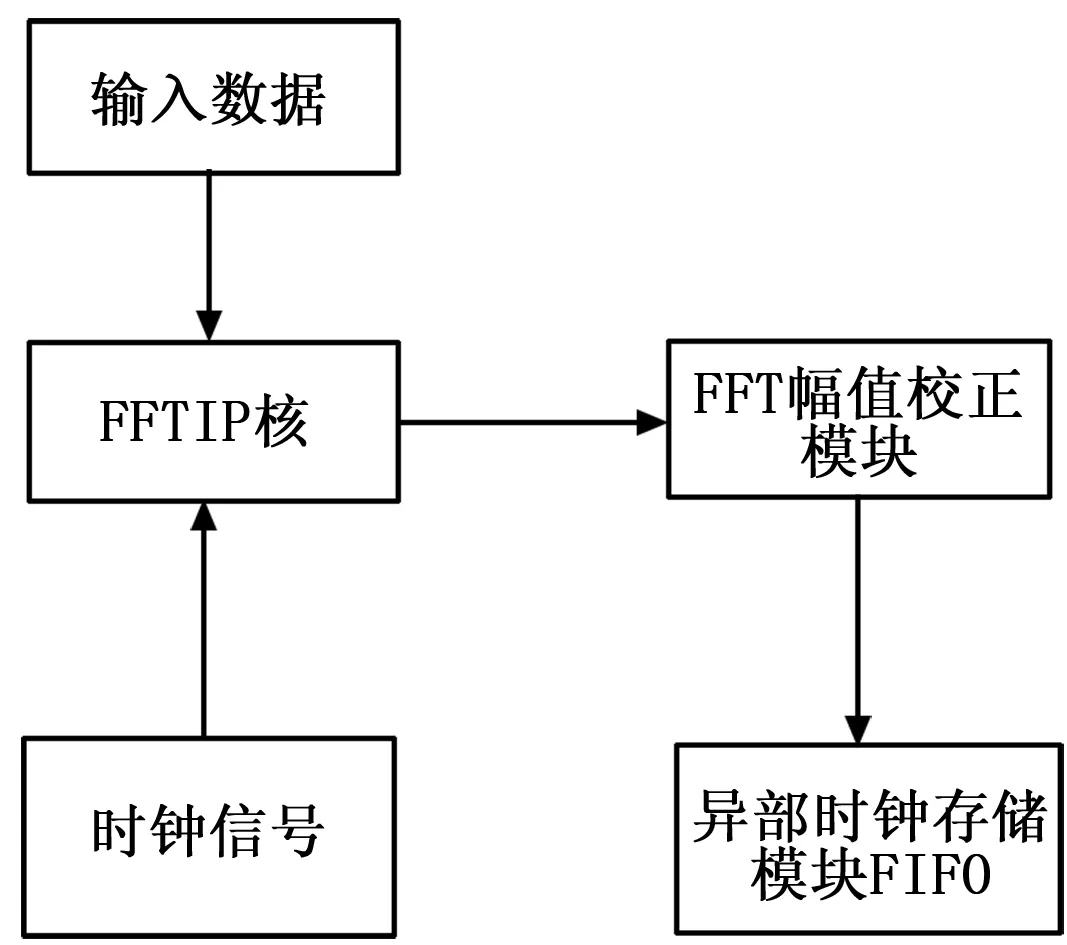
图5 FFT算法模块
其中FFT幅值校正模块对FFT功能IP核输出的结果进行进一步处理。参考官方提供的数据手册,从FFT功能IP核输出的数据还要与旋转因子相乘,根据旋转因子的精度位数,要对数据进行添加补位码的操作,此模块即用以实现此功能。
由于FPGA中FFT的高速处理与系统时钟不匹配,因此需要一个异步时钟域存储模块作为缓冲,从而将两者衔接,使整个系统正常工作。
3 实测数据处理结果与分析
本节采用实测数据成像对上述方法进行了验证。雷达和实验参数如下:GNSS卫星采用俄罗斯卫星GLONASS 732,工作频率为1 603.687 5 MHz,信号带宽为5 MHz。卫星离地面高度为22 000 km。成像场景位于英国伯明翰大学图书馆附近,合成孔径时间为5分钟。成像场景照片如图6所示。
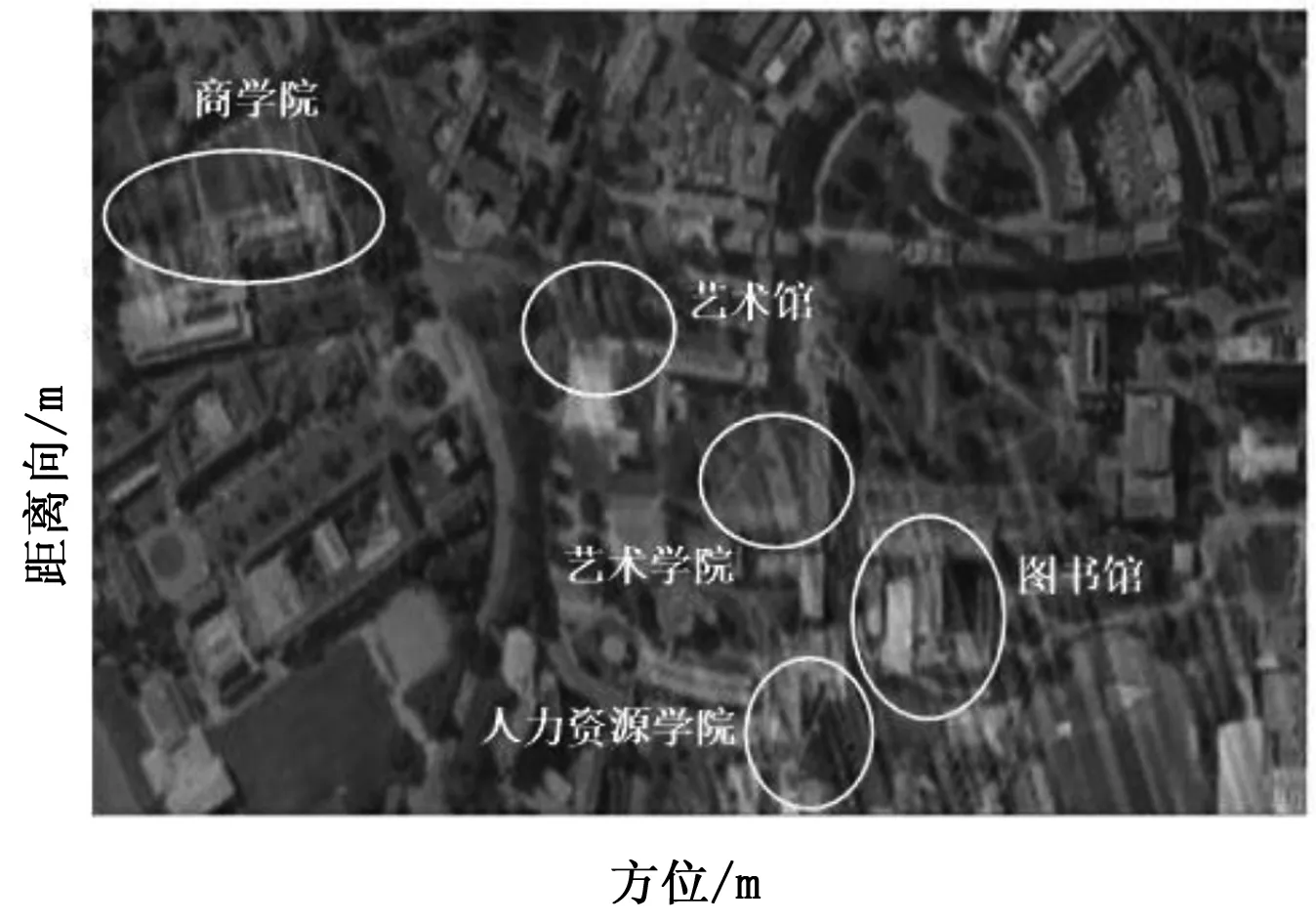
图6 成像场景照片
可以看出,该成像区域有5处较明显的目标,其它区域为草坪和树木。因此,在成像结果中,预计在明显目标处将获得强反射,而其它区域的反射拟较弱。
图7为采用本文提出的FPGA成像处理方法处理得到的图像

图7 采用本文提出的FPGA成像方法得到的图像
图上的最强点为雷达波天线直接接收GNSS直达波成像结果,像点位置为坐标原点,与预期相符。图8给出了该成像场景光学卫星的图像和图7的叠加结果。

图8 图7与光学图像叠加结果
可以看出,两幅图像中主要目标像点的位置一致。此外,在光学卫星图像中观察到的若干弱反射区域,如草坪、树木等,雷达图像中显示的回波均较弱,与预期相符。
4 结束语
本文研究了基于BP算法的外辐射源合成孔径雷达硬件成像处理方法。该方法运行在Intel DE1-SOC FPGA平台上。通过构建计算距离模块、FFT模块、指数运算模块、插值模块,实现了一整套BP算法的硬件处理流程。
文中最后给出实测数据进行处理得到的二维图像结果,并将该结果与相同场景的光学图像进行了对比,验证了本文提出的成像处理方法的有效性和准确性。

