雷达接收信号循环平稳特性控制研究

(中国人民解放军66350部队 技术室，河北 保定 071000)

0 引言

雷达接收到的信号并不只是一个辐射源发射的，而是由多个独立的辐射源发射相关信号，所有信号被雷达接收后组成混合信号，因此，在实际应用环境中，混合信号保持循环平稳特性是一个值得研究的问题[1]。在被动雷达接收到的混合信号中，独立的混合信号循环谱密度函数等于各个信号自身循环谱密度函数叠加之和；在主动雷达接收到的混合信号中，对两个相干信号同时入射的情况加以分析[2]。传统采用信号参数估计控制方法，利用特定循环频率处的谱相关函数实现对雷达接收信号循环平稳特性控制研究，由于幅度调制信号循环频率是载频处循环频率的两倍、编码信号循环频率与信号码速率谱相关函数一致，导致雷达接收到的混合信号出现时延；当参数满足一定条件时，混合信号循环相关函数在循环频率处不再具有明显的非零属性，造成信号循环平稳特性无法得到有效控制。因此，采用遗传算法对雷达接收信号循环平稳特性控制展开研究。

1 雷达信号接收原理

天线、接收机、和信号处理器组成雷达，发射机的主要任务是对外发射信号，来自不同辐射源又反射后的回波信号由雷达接收机接收，再经过信号处理器进行信号处理，这是一套大致的步骤。磁波源是由各种通信信号组成，主要是通过上述设备反射回来的。这主要由于雷达无法发射主动性质的电磁波。实现目标探测[3]，雷达信号接收原理如图1所示。

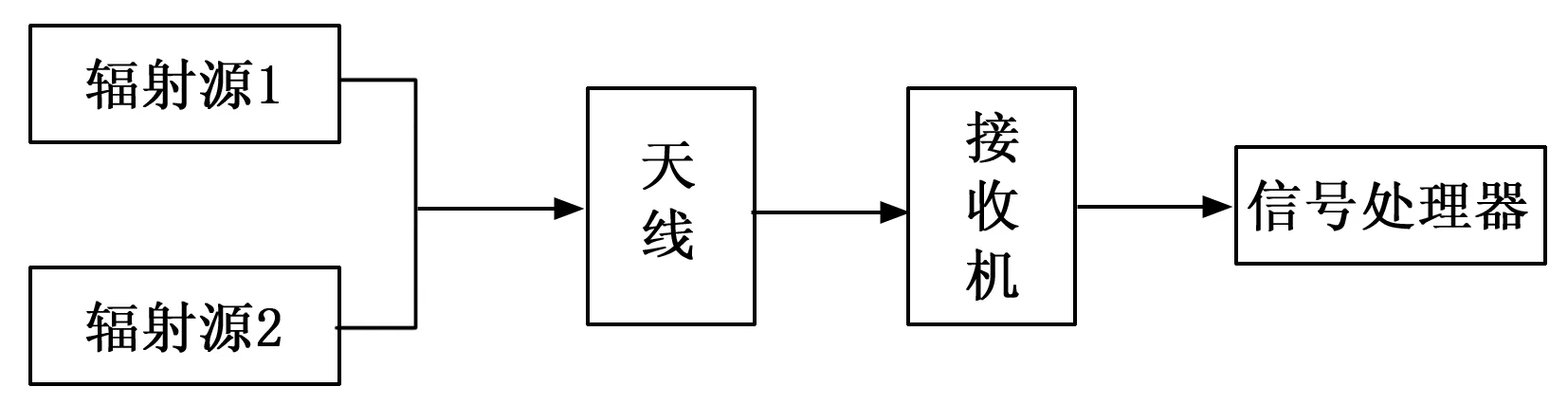
图1 雷达信号接收原理图

辐射源发送的信号是具有独立性的，彼此之间并无关联，如果雷达同时接收多个由辐射源发射的信号，那么将这些信号统称为混合信号，该信号分量是相干的。

2 混合雷达信号循环平稳特性控制分析

根据上述雷达信号接收原理，对混合信号循环平稳特性控制展开分析。针对混合信号的接收方式有两种，分别是被动雷达接收和主动雷达接收。其中，被动雷达可接收来自不同辐射源发射的独立信号，主动雷达可接收来自不同设备发射的电磁波信号[4]。在独立信号接收过程中，采用感应控制方式，可实现对信号循环平稳特性的控制；而在不同设备发射的电磁波信号接收过程中，会出现时延问题，为了解决该问题，提出了遗传算法对雷达接收信号循环平稳特性进行控制。

2.1 构建非线性规划数学模型

以实时采集到的雷达接收信号数据为基础，以主动雷达混合信号延误时间为目标，构建非线性规划模型[5]。采用Webster延误方法，计算每次接收到的混合信号平均延误：

(1)

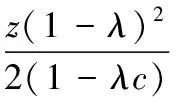
根据上述内容构建非线性规划数学模型，即为总的延误时间：

(2)

公式(2)中：pij为第i个相位的第j接收器处的信号流量；cij为第i个相位的第j接收器处的信号饱和度；λi为第i个相位的有效接收信号时长与周期时长的比值。

2.2 约束条件设立

根据构建的非线性规划数学模型，设定约束条件：

1)充分考虑通过接收器时的信号接收安全需求，将每个相位的最短接收时间设置为大于等于某值e，因此，每一个相位配时需满足：

e≤ti≤z-T-10×3,i=1,2,3,4

(3)

公式(3)中，ti为第i个相位的有效接收信号时长；T为总延时耗费的时长。

2)充分考虑饱和度限值约束条件，将某个时间段内的周期在合理信号配时条件下，各个相位的饱和度都不大于1.0，避免造成某个接收器接口处出现信号拥堵的现象。假定各个接收器接收端口饱和度都不大于0.9，那么饱和度约束条件为：

(4)

公式(4)中：p为实际信号流通量；N为信号通行能力；s为饱和流量；ge为有效接收信号时长。

2.3 采用遗传算法控制信号时延

遗传算法是一种通过模拟自然进化过程搜索的最优控制时延方法。每个个体实际上是染色体带有特征的实际信号[6]。染色体作为遗传物质的主要载体，其内部表现出来的是某个信号的成分，它决定了信号频率大小，因此，在一开始需要实现从信号频率变量到控制信号大小的映射，也就是编码工作。由于仿照信号编码的工作很复杂，往往进行简化，初代种群产生之后，按照适者生存和优胜劣汰的原理，逐代演化产生出越来越好的近似解，在每一代，根据问题域中个体的适应度大小选择个体，并借助于自然遗传学的遗传算子进行组合交叉和变异，产生出代表新的解集种群。这个过程将导致种群像自然进化一样的后代种群比前代更加适应环境，末代种群中的最优个体经过解码，可以作为最优解来实现信号时延的有效控制[7-9]。

2.3.1 变量编码

利用实数对变量进行编码，编码的长度即为变量的个数。在雷达接收装置中，对一个4相位接收端口，设a1、a2、a3、a4为变量，其中a1、a2、a3分别为第1、2、3相位的有效接收信号时长，在固有的损失时间基础上，第4相位的有效接收信号时长可表示为：a4=T-a1-a2-a3，那么编码可表示为：a1、a2、a3。

2.3.2 遗传操作

(1)选择操作。

保留2个进化与当代为止最优的信号，采用双亲与后代竞争方式，利用轮盘选择算子，将所有待选择的信号按照适应程度由高频率到低频率排序，第i个信号个体生存概率为：

P(i)=F(1-F)i-1

(5)

公式(5)中：F为选择压力。

在每个信号生存概率求出后，可计算个体选择概率，按照轮盘赌博方式进行选择，进而产生后代。

(2)交叉。

交叉概率对种群中所有信号进行随机配对，如果信号数量为奇数，那么可随机去掉一个信号个体[10]。每一个在[0，1]范围内的配对信号都会产生一个随机数r，如果r小于交叉概率，那么配对的信号需要进行交叉操作，交叉规则如下所示：

(6)

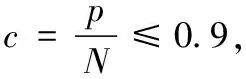
(3)变异。

变异概率对种群中任何一个信号个体，在[0，1]范围内的配对信号都会产生一个随机数r，如果r小于变异概率，那么配对的信号需要进行变异操作[11]。如果生成的个体为非正常个体，那么需要重新配对，直到获取合法个体为止。采用遗传算法对雷达接收信号循环平稳特性控制过程，具体描述如下所示：

1)将雷达接收的混合信号进行初始化处理，设定信号种群数目、染色体长度、迭代总数、交叉概率和变异概率，根据上述编码结果，可获取变量个数，即为：a1、a2、a3；

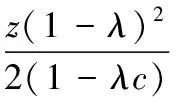
3)以该染色体数目计算个体函数适应值；

4)将父—子代产生的所有信号个体进行重新排列，构造出具有秩序的新种群。

5)按照交叉概率对上述随机产生的信号个体进行交叉处理；

6)按照变异概率对上述随机产生的信号个体进行变异处理；

7)验证调整幅度信号循环频率与载频处循环频率是否保持一致，如果没有，则需转到步骤(3)，重新计算个体函数适应值；如果保持一致，则需输出最佳信号配时方案。

在控制研究过程中，构建非线性规划数学模型，根据每次接收到的混合信号平均延误时间计算总的延误时间。设立约束条件，根据总的延误时间，调整幅度信号循环频率与载频处循环频率保持一致，实现信号循环平稳特性的有效控制，并改善了主动雷达接收信号出现的时延问题。

3 实验结果与分析

为了验证采用遗传算法雷达接收信号循环平稳特性控制研究的合理性，需将实验分成被动雷达信号与主动雷达信号的循环平稳控制两部分进行，并对实验控制效率结果总结。实验的方法步骤主要分为：

1)分别采用改进控制方法和传统控制方法对被动雷达接收信号循环谱密度函数包络情况进行测试，得到实验对比结果如图2所示；

2)分别采用改进控制方法和传统控制方法对主动雷达接收信号循环谱密度函数包络情况进行测试，得到实验对比结果如图3所示；

具体实验过程描述，以及实验结果分析如下：

3.1 被动雷达信号

被动雷达信号依靠第三方辐射源对目标发射电磁波，接收回波信号，获取目标信息。以相互独立的等功率信号对控制研究结果进行验证，设雷达接收信号载频为1000 Hz，带宽为20%，码率为500 Hz。将传统控制方法与采用遗传算法的控制方法信号循环谱密度函数包络情况进行对比，结果如图2所示。

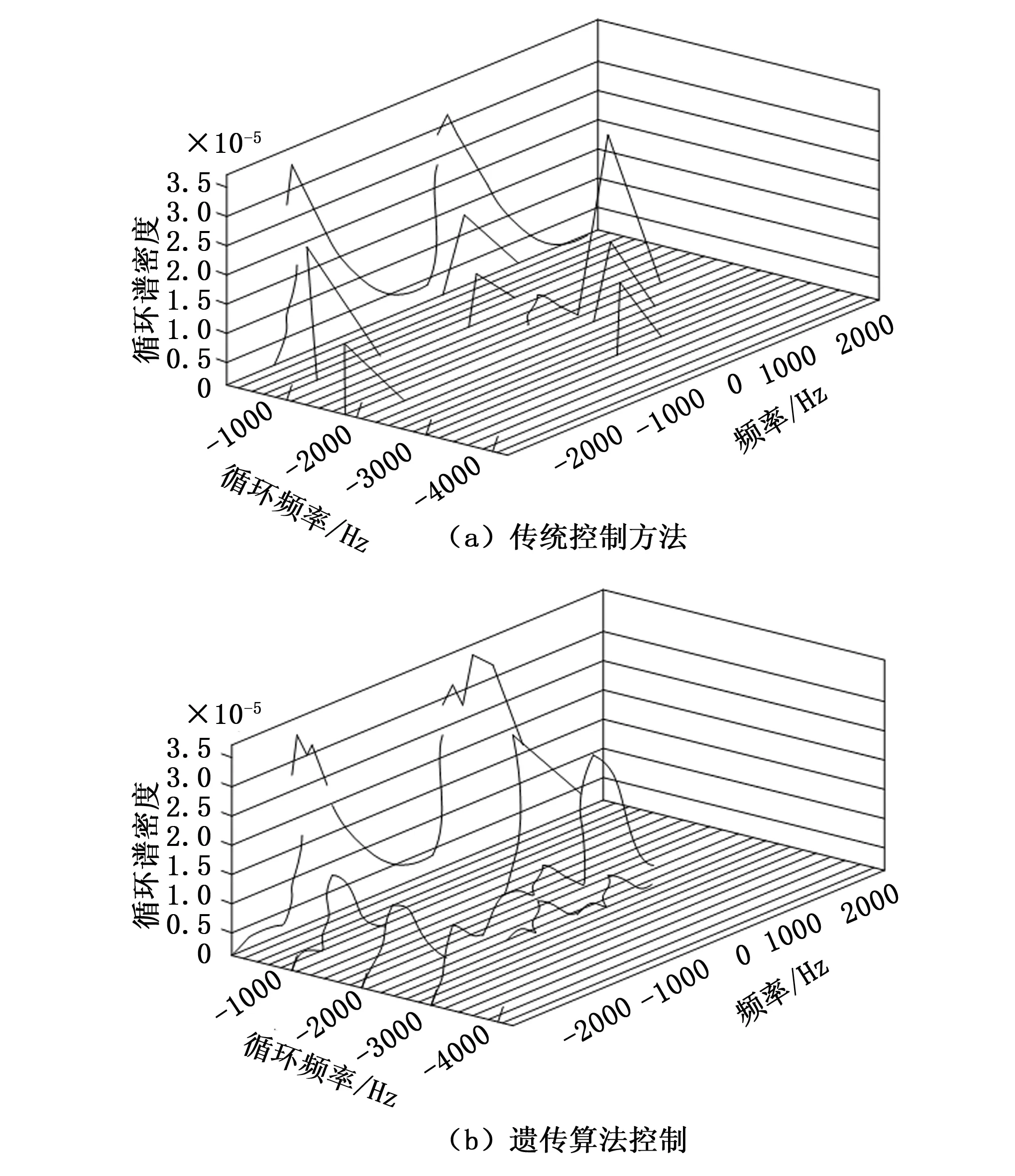
图2 两种控制方法被动信号循环谱密度函数包络情况

由图2可知：传统控制方法循环谱密度所呈现的线型为直线，虽有包络凸起，但是基本与原始包络为“一线”状态，最高循环谱密度达到3.5×10-5左右，而采用遗传算法循环谱密度所呈现的线型为曲线，凸起的包络呈分散状态。从对比结果来看，采用遗传算法有限采样限制了信号接收强度，促使控制信号循环谱密度偏差较小。

根据两种控制方法的信号循环谱密度函数包络情况，将传统方法与遗传算法对控制程度展开对比分析，结果如表1所示。

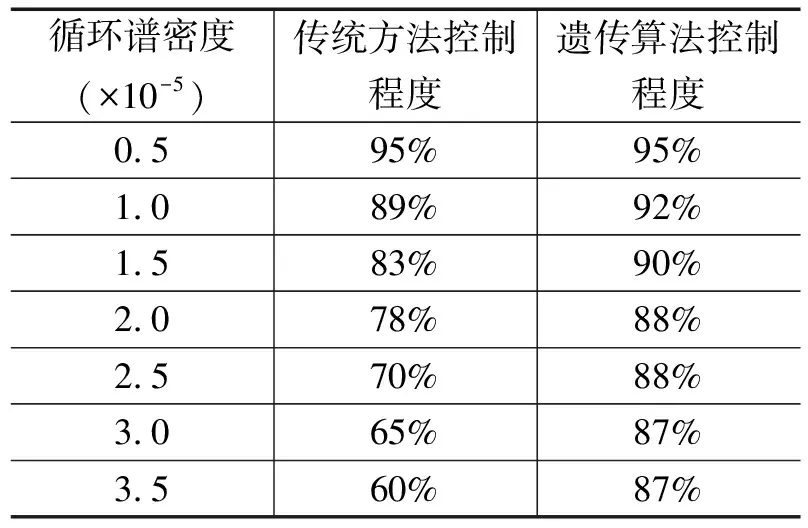
表1 两种方法在被动雷达信号下的控制程度对比

由表1可知：当循环密度为0.5×10-5时，采用传统方法控制程度达到95%，同样采用遗传算法控制程度也可达到95%，随着循环密度的变大，采用传统方法控制程度逐渐下降，而遗传算法控制程度也有小幅度下降趋势。当循环密度为3.5×10-5时，采用传统方法控制程度下降到60%，而遗传算法控制程度下降到87%。由此可知，当循环密度达到最大时，两种对循环平稳特性的控制程度相差27%，在被动雷达信号状态下，采用遗传算法控制能力较强。

3.2 主动雷达信号

主动雷达依靠自身定向辐射电磁波，接收目标反射回波进行探测，获取目标的方位、距离等信息，还可以通过回波中的多普勒频移，计算出目标径向速度等信息。主动雷达接收信号载波频率可达到1000 Hz、相对带宽为20%，使用相同功率信号时，会出现时延。当信号在循环频率为2 000 Hz时，将传统控制方法与遗传算法控制的信号循环谱密度函数包络情况进行对比，结果如图3所示。

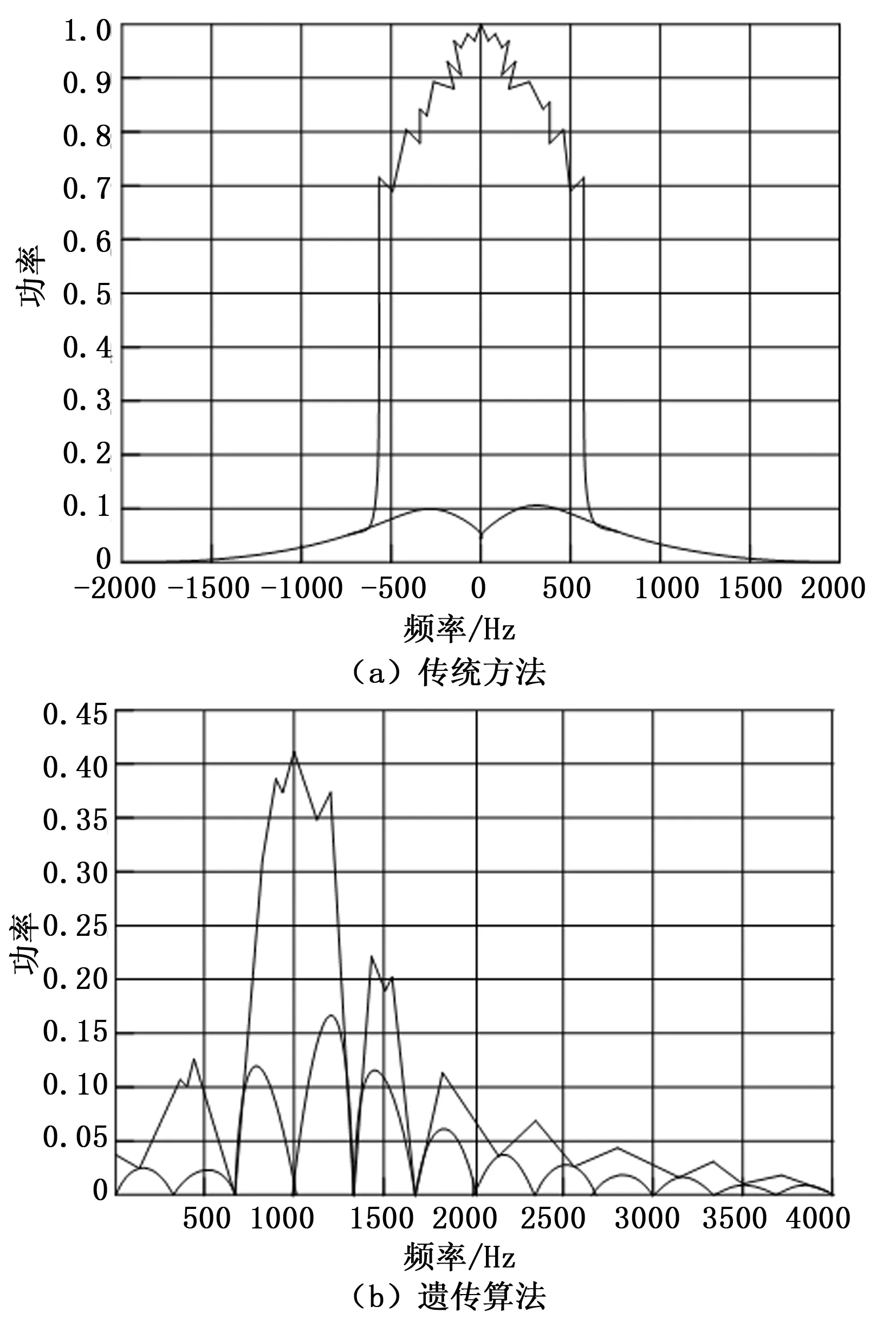
图3 两种控制方法主动信号循环谱密度函数包络情况

由图3可知：采用传统方法具有明显失真现象，在频率为0 Hz处功率达到最大，但是无论频率增或减，功率都会大大降低，且呈对称性；而采用遗传算法在频率为1 000 Hz时，具有明显非零循环函数调动现象，有可能会出现大幅度降低，但是由于信号时延，促使信号与信号之间的传递也出现时延，此时将两个循环频率处的频谱密度函数信息结合加以利用，可有效改善控制的平稳性。

将传统方法与遗传算法对控制程度在相同信号频率下展开对比分析，结果如表2所示。

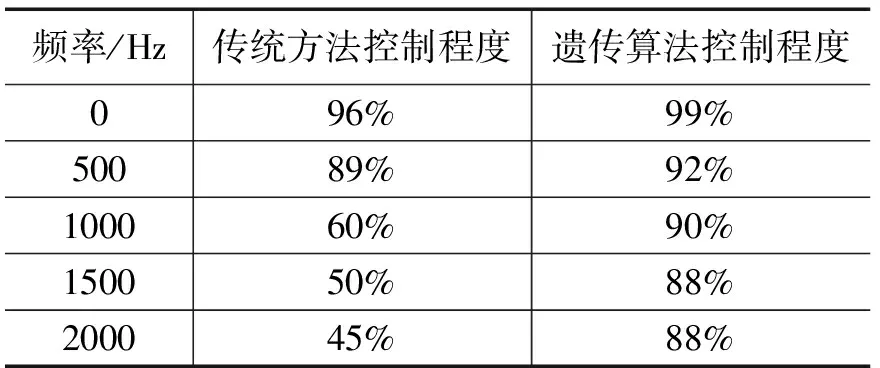
表2 两种方法在主动雷达信号下的控制程度对比

由表2可知：当频率为0 Hz时，采用传统方法与遗传算法控制程度都可达到95%以上，但是信号频率一旦增强，两种方法控制程度都有所下降。当频率为2000 Hz时，传统方法控制程度下降到45%，而遗传算法控制程度仍然较高，为88%，两者相差43%。由此可知，在主动雷达信号状态下，采用遗传算法控制能力较强。

3.3 实验结论

根据上述实验内容，可得出实验结论：

1)传统控制方法循环谱密度所呈现的线型为直线，而遗传算法循环谱密度所呈现的线型为曲线，当循环密度为0.5×10-5时，两种方法控制程度达到了最佳状态，但是随着循环密度变大，两种方法控制程度出现了较大差距，遗传算法控制程度比传统方法控制程度高出27%，由此可知，在被动雷达信号状态下，采用遗传算法控制能力较强。

2)当频率为0 Hz时，两种方法控制程度都可达到99%；当频率为2000 Hz时，两种方法控制程度相差最大，且遗传算法控制达到平稳状态，不再下降，由此可知，在主动雷达信号状态下，采用遗传算法控制能力较强。

无论是在被动雷达信号状态下，还是主动雷达信号状态下，采用遗传算法控制能力都比传统方法控制能力强。

4 结论与成果

在实际雷达接收信号循环平稳特性控制过程中，实时采集信号流的相关数据，发送至信号处理器中进行相关步骤的处理，采用遗传算法调整幅度信号循环频率与载频处循环频率，保持两者频率大小一致，实现信号循环平稳特性的有效控制。为了确保控制结果的合理性，充分考虑接收器的接收端口饱和度限值，以各个相位进出口总延时作为目标展开研究，该研究方式不仅使被动雷达信号接收的循环平稳特性得到了有效控制，还改善了主动雷达信号接收出现的时延问题。该项目的研究体现了理论与实际的结合，并通过实验得到了证明。但是，在进行实验过程中，由于时间存在差异，导致结果的比较也只是定性评价，如果想要定量评价，还需模拟真实环境，降低结果产生的误差。