一类航天器控制系统反馈调度方法研究

, ,

(北京控制工程研究所，北京 100190 )

0 引言

信息物理系统(cyber-physical systems)是近年来控制与计算机领域兴起的一个重要研究方向。其主要内容是将系统中控制、计算、通信的过程当作一个整体来考虑，研究其中信息系统行为与对象物理状态间的互动关系，从而进一步提升系统性能[1-2]。而基于对信息系统状态测量并在线对系统计算或通信资源进行分配的反馈调度方法就成为了CPS研究中的一条重要技术路线。

与此同时，随着人类在太空的活动日益频繁,宇航任务模式也更加多元,进一步降低太空活动的成本,提高航天器自主任务管理能力的需求也不断提高。如何进一步提高航天器控制系统自主运行的能力、提升控制性能、节约能量消耗、提升容错能力和故障判读、处置[3]能力，也成为航天器控制系统研究中的关键问题之一。

在已有的国内外研究成果中，在文献[4]中首次提出了反馈调度的概念和一般的设计思路。文章对嵌入式微处理器的利用率和计算任务的截止时间丢失率进行实时测量，将其与各自设计值的误差作为模型输入，建立误差传递函数。通过不断调整给各个计算任务分配的任务周期，对CPU利用率进行动态调节。文献[5]研究了控制性能与微处理器电压之间的关系。其将处理器期望利用率，各个任务最大、最小执行时间等参数共同输入调度模型，利用弹性调度算法，设计出了一套考虑处理器能耗的任务调度方法。文献[6]将反馈调度方法应用在一类机械臂的控制系统设计过程中，将控制算法分解成不同的周期性任务，按照其数值大小分配权重，从而动态分配计算资源，在保证性能的前提下达到了节约计算资源的目的。文献[7]将模糊控制方法应用于反馈调度算法的设计中。在文章中其应用双层的模糊逻辑，首先使用第一层模糊逻辑来调整任务优先级从而降低截止时间丢失率，再应用第二次模糊逻辑在线调整和分配任务周期来控制处理器计算资源的利用率。与传统调度方法相比较，在相同处理器利用率条件下达到更高控制精度。文献[8]是设计了一种考虑在可调度性约束条件下，基于固定优先级的单调速率调度的多任务系统最优任务周期分配算法。并通过物理实验验证了算法的有效性。

文献[9]是航天器容错控制与故障诊断方面的一篇比较权威的综述。从文中可知，目前航天器控制系统的故障研究主要集中在执行机构(如推力器、反作用轮)以及测量机构(陀螺、敏感器)的故障上,而且多以开环的故障诊断方式为主。一般方法是利用先进控制算法在执行机构故障时设计欠驱动的控制算法，以及应用滤波估计方法在无直接测量输出情形下对状态量进行重构与估计。而对于航天器上嵌入式计算与通信系统的故障研究较少，仅有在网络控制领域会分析数据丢包等故障,但诸如处理器因为供电电压不足或多核处理器部分故障导致的降频等故障形式,以及相关的容错控制方法未见研究成果发布。

本文主要结合已有的反馈调度方法，设计了一种基于对任务执行时间测量的在线反馈调度与控制算法。能够通过调节任务执行周期，一方面保证航天器在轨工作过程具有满足指标的高控制精度，另一方面可以使航天器在轨的非工作过程通过延长控制周期，来降低整个轨道周期的平均能耗。与此同时，在处理器发生降频故障时，能够自主调节任务的周期分配，保证航天器姿态稳定。文章结构如下：第一部分引言介绍文章的主要研究内容及背景；第二部分给出所研究问题的数学模型；第三部分介绍所提出的反馈调度与控制算法；第四部分为仿真验证；第五部分为文章的结论。

1 问题描述

航天器线性化姿态动力学模型可描述为[10]:

(1)

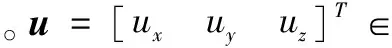
(2)

联立式(2)可得到系统模型的状态空间表达式:

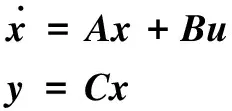
(3)

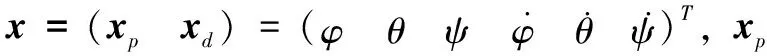
其中:

星上控制系统采用计算机控制模式，所以将式(3)进行离散化处理，得到：

x(k+1)=F(T)x(k)+G(T)u(k)

u(k)=-Kx(k)

(4)

其中:K为反馈增益阵，根据控制算法求得，T为采样周期。一般来说，对于计算机控制系统越小的控制周期能够实现更高的控制精度。而同时越小的周期就意味着系统需要将更多的CPU分配资源给控制系统。对于低轨道航天器而言，其轨道周期约95 min，但其中需要航天器进行高精度指向控制的工作时段只有约10 min，其余时间均可认为是控制系统的非工作时段。所以在任务设计时可以在工作时段给控制系统分配较多的计算资源，提高控制精度，而在非工作时段可将资源分配给如数据处理、通信等系统，提高任务完成质量，优化航天器的整体性能。

航天器的控制任务在星载嵌入式系统上具体实现时，要将数据采集、计算、输出的过程分解为顺序执行的几个周期性子任务[11]。对于微小型航天器控制系统而言，由于功耗和体积限制苛刻，所以各个测量敏感器需要共用一块CPU。其一阶状态量xp以及二阶状态量xd通过MEMS地球、太阳敏感器和三轴陀螺仪进行采集。计算单元在一个控制周期开始时发出采集指令，在经过一段执行时间后，所采集到的状态量进入系统内存中，在控制算法所需的状态量均采样得到之后，一同送入处理器，代入控制算法进行运算，最终将计算机所生成的控制指令发到执行机构。整个控制任务的周期为采样周期T，xp的采集的子任务执行时间为cp，xd的采集子任务执行时间为cd，最终控制算法执行及输出子任务执行时间为co。在此过程中，CPU用于控制任务的利用率可表示为Ua=(cp+cd+co)/T<1。在相同的软硬件环境内，CPU功耗E与利用率直接相关，存在表达式:

(5)

整个控制任务模型可以描述为τc(cp,cd,co,T,Ua),对于传统的航天器控制系统而言，一般在设计过程中就确定一个固定参数的τc。不同任务间留够充足的时间裕量避免时序冲突。这种思路的优点是便于进行不同系统间的衔接，设计难度较低。但随着对航天器集约化要求及容错能力日益提高，就需要设计一种能够自主灵活分配资源，处置故障的调度与控制算法。

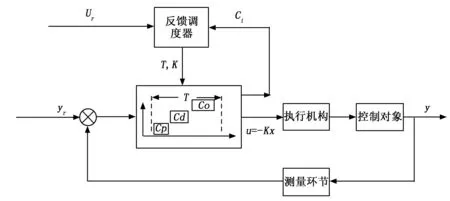
图1 反馈调度算法结构图

2 算法描述

本文所研究的此类反馈调度算法，其实现过程主要分为三个步骤：第一是任务执行时间测量；其内容是对处理器在一个控制周期内所需执行的各个任务的具体耗时进行测量与估计；第二是资源调度；其核心是根据上层软件分配给控制系统的可用处理器利用率以及控制任务所需的执行时间，来调整控制周期。第三是反馈增益计算；即根据新的控制周期，来重新调整控制算法中的控制增益。如果不进行调整，有可能造成控制性能下降甚至系统发散。本反馈调度算法结构如下所示。

其中Ci为任务执行时间，Ur为系统给控制任务的CPU利用率，yr为控制系统的参考输入。

2.1 执行时间测量

Ci为反馈调度器对CPU内不同任务执行时间的测量。一般来说可以通过对计算单元内时间片的判读得到，但其中会存在因量化效应、时间抖动产生的噪声，需要进行滤波估计。而反馈调度算法的另外一个重要功能就是当计算单元发生故障，导致执行时间发生变化时，传统的固定参数的优先级调度方法会产生计算超时等时序问题，导致系统失控，而反馈调度方法能够自主调整任务周期，调整控制增益，保证控制系统稳定运行。

执行时间测量模型可描述为:

(6)

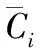
(7)

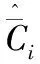
2.2 资源调度

Ur为CPU分配给控制系统的参考利用率，一般由操作系统及任务规划软件决定。

定义调度任务模型为τs(cs,Ts)，一般情况下为保证计算资源有效利用及系统稳定，调度周期不易过小，设定Ts>3T。调度任务的作用就是根据给系统给控制任务分配的CPU利用率，来对控制周期进行分配，并计算相应的控制增益。则根据式(7)，有控制周期表达式为:

(8)

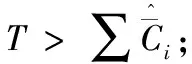
(9)

2.3 控制增益计算

控制增益计算一般应用计算机控制理论，根据系统状态矩阵及采样周期计算控制增益阵。本文中采用离散最优控制方法，将系统式(4)带入Ricatti方程:

FTSF-S-FTSG(GTSG+R)-1GTSF+Q=0

其中:正定阵Q和R为二次型指标的加权阵，表达式为:

解得对称阵S，再解出:

K=(GTSG)-1GTSF

(10)

其中:Q越大则得到的控制精度越高，而R越大则控制输出则越小，Q和R的选择决定了控制精度与控制输出的折中关系，同时也需要谨慎调节以避免执行机构输出达到饱和。

此时就可以保证对于调度算法给出的任务周期T，找到一个对应的最优反馈增益阵K。

3 仿真分析

仿真研究的任务背景是一个微型低轨道航天器，工具使用Matlab中Truetime工具箱。仿真参数如表1所示。

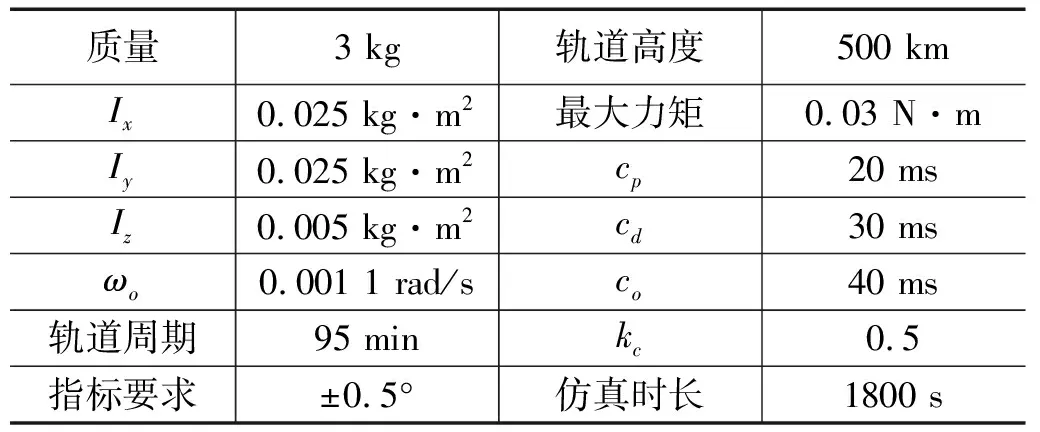
表1 仿真参数设置[12]

xdr=[0.57sin(t/40),-0.57cos(t/50),

0.57sin(t/60)]Tdeg/s

在此设定航天器的轨道周期在t∈[600,1 000]s时为工作弧段，要求在此时段内达到指标跟踪精度要求，以便于载荷正常工作。而在其余非工作时段内，要求航天器姿态保证跟踪误差较小，保证航天器姿态可控即可。而在t=1 200 s时，给系统注入计算单元发生故障，验证反馈调度系统的容错能力。此时处理器降频至0.25f，则任务执行时间均变为标称值的4倍(考虑控制任务代码执行速率均与处理器速度相关)。

根据以上所交代的任务背景，可得到各个时段内控制系统分配到的计算单元的任务参数为:

图2为计算单元利用率变化曲线，实线为计算单元利用率的参考输入，虚线为根据为系统实际利用率。可以看出本文给出的反馈调度算法对利用率需求变化具有很高的跟踪精度。特别是在1200 s故障注入时刻之后，如图所示，调度算法经过30 s，即3个调度周期后使系统计算利用率恢复到参考输入水平。

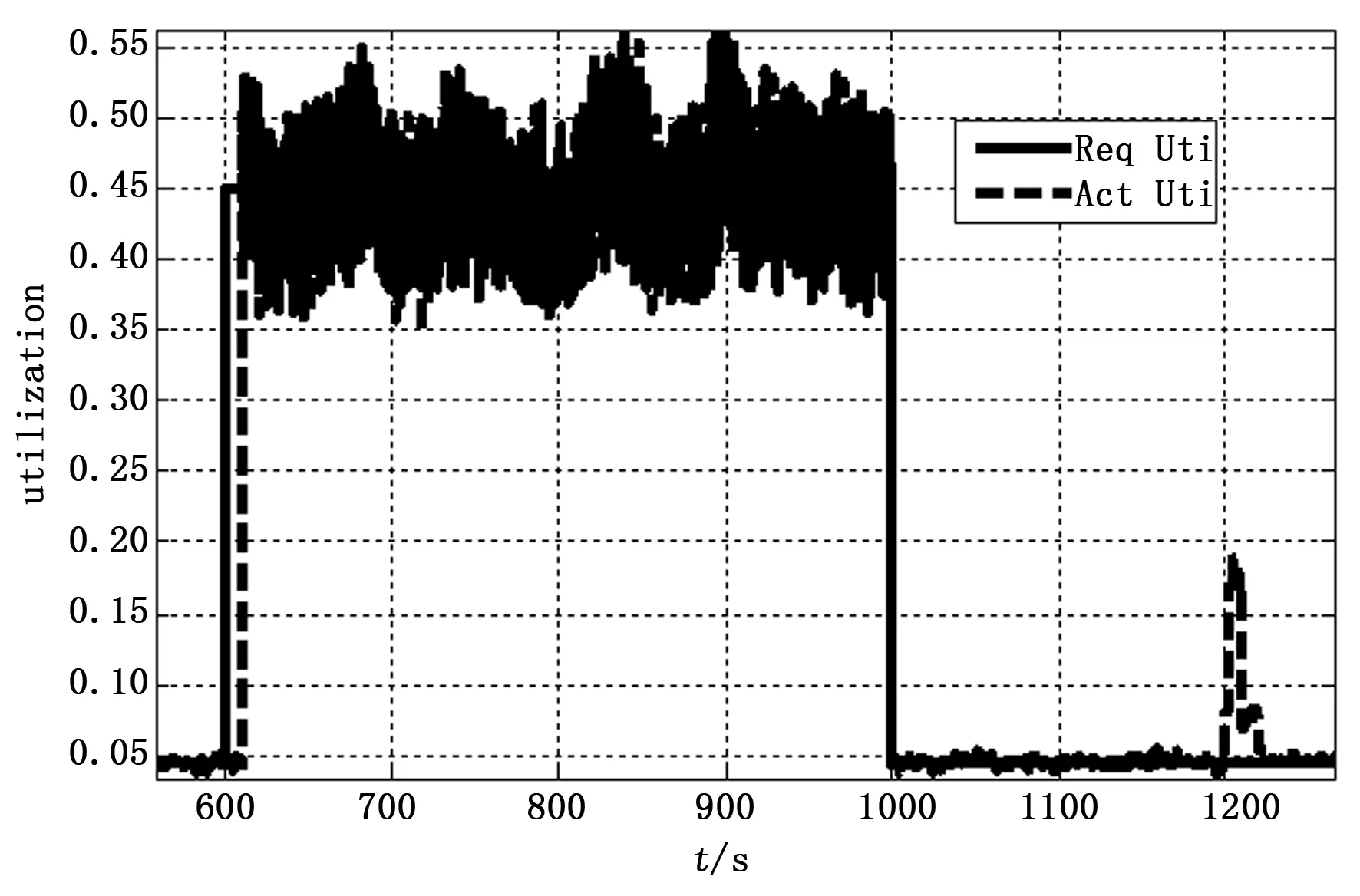
图2 CPU利用率变化曲线

图3为航天器在轨姿态角状态变化曲线，从图3可以看出，在整个仿真时间段内，即使在1 200 s故障发生后内角度跟踪精度均保持在±5°之内。在所设置的航天器工作弧段600～1 000 s内，系统姿态控制精度从±1.5°提升到±0.5°, 达到性能指标要求。而对于传统控制与调度方法，要保证工作弧段性能指标要求，就需要在整个周期内保持控制精度在±0.5°之内，这就需要计算单元给控制系统分配固定的计算资源以保证任务要求，在非工作时段就会造成一定的计算资源浪费及过多的能耗损失。所以本文提出的反馈调度方法与传统方法相比，根据式(5)可知，在一个轨道周期之内控制系统能够极大的节约CPU能耗及计算资源。

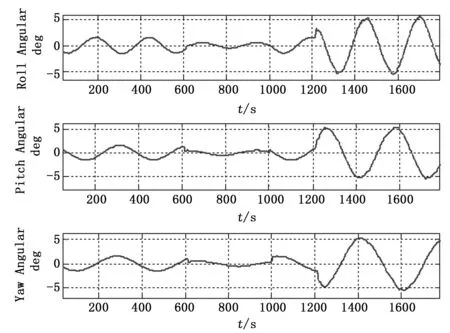
图3 角度变化曲线

图4～6为基于Truetime工具箱得到的计算单元内部的工作时序仿真结果。从图4可知，在600 s之后因为航天器进入指向跟踪的工作弧段，系统给予控制系统的计算资源有所增加，此时的控制任务周期从2 s降为0.2 s左右，而同时由图3所示的系统状态变化曲线上也能反映在得到更多CPU资源后，航天器的控制精度明显提高，验证了反馈调度算法能够动态分配资源，提高系统整体性能。

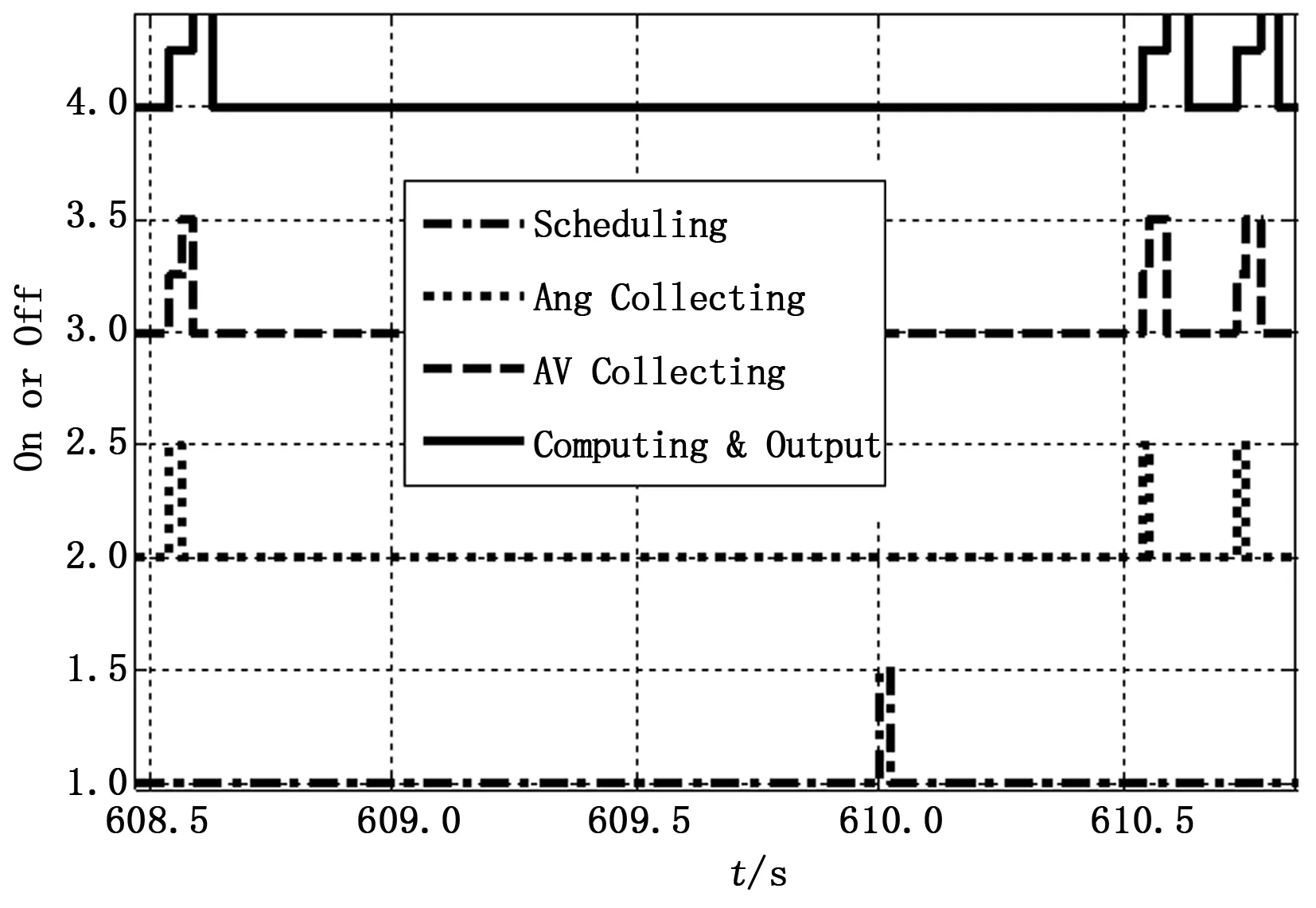
图4 工作时段时序变化曲线

由图5可以发现，在1200 s对航天器进行了故障注入之后，控制任务中的各个子任务的执行时间显著增加。但从图6可以看出，在1210 s之后，经过一个调度之后，系统的控制周期开始逐渐变大,说明反馈调度系统已经及时感知到了故障的发生，并采取了相应的应对策略。

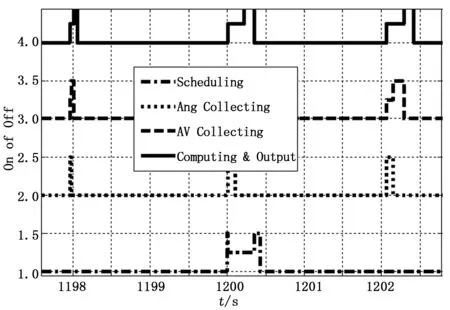
图5 故障时刻执行时间变化

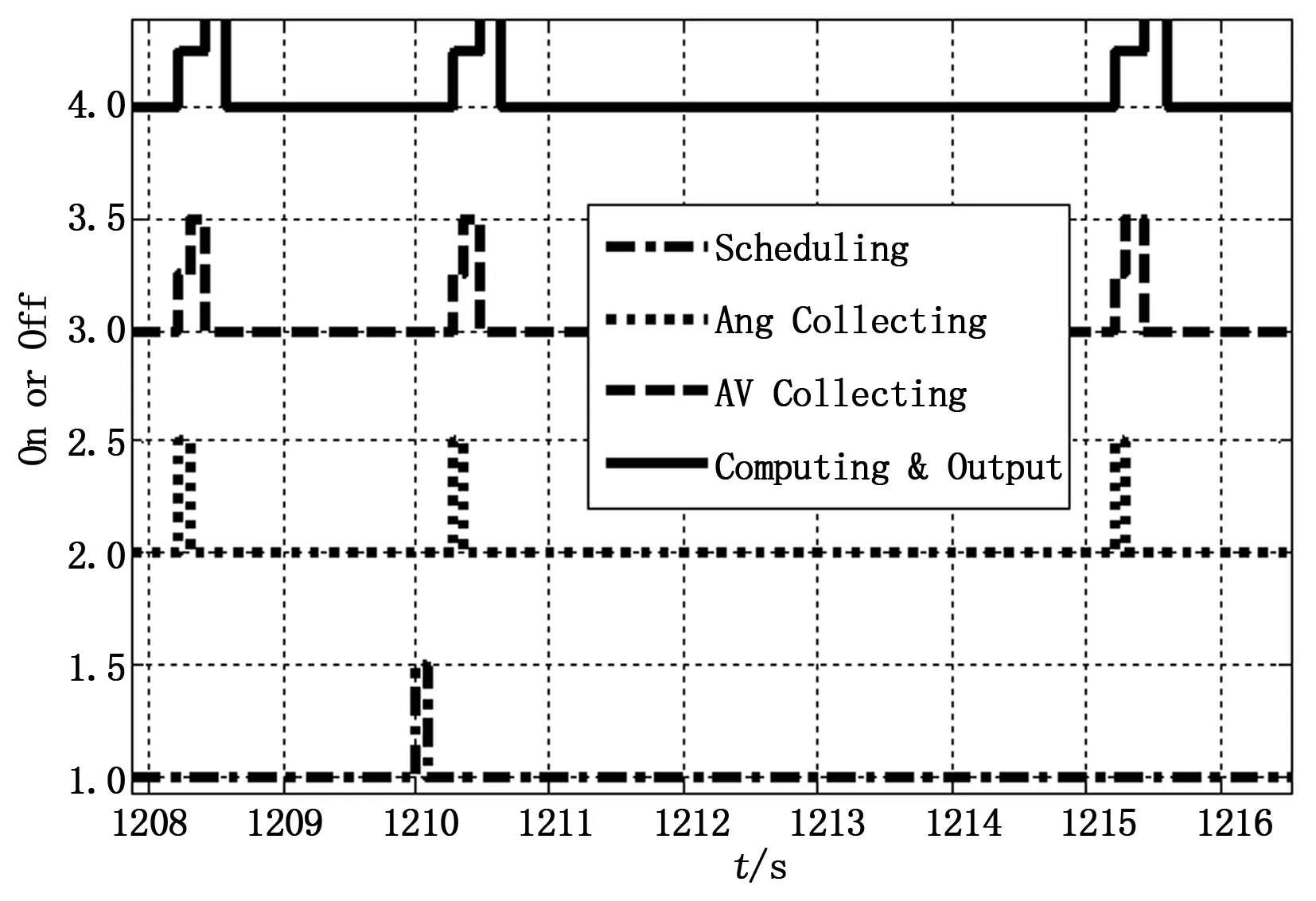
图6 故障后任务周期变化

同时这也验证了反馈调度算法能够通过调整控制周期来保证系统的实际CPU利用率的恒定，从而保证控制系统内部任务之间以及控制系统与其他需要使用CPU的系统间不会发生时序冲突，保证整个航天器系统能够稳定运行。

4 结论

本文介绍了一类应用于航天器控制系统的动态调度CPU使用率并调整控制增益的反馈调度方法。通过仿真分析，该方法能够在航天器在轨的工作与非工作时段动态分配系统的计算资源。从而使得航天器控制系统具有了在工作时段提供高精度指向控制，满足任务需求，在非工作时段保证姿态稳定，节约系统功耗及计算资源的动态资源管理能力。同时在遇到星上计算机故障时，能够通过调整任务周期的方式，保证姿态稳定，达到容错控制的目的。