基于KPCA-DFNN海洋微生物发酵过程软测量建模

，，，

(1.苏州工业园区职业技术学院，江苏 苏州 215123；2.江苏大学 电气信息工程学院，江苏 镇江 212013)

0 引言

海洋微生物作为微生物的一类，因其生存的海洋具有特殊的环境，故其所产生的酶与其他微生物所产生的酶相比具有更加独特的性质，如耐低温，耐碱性，PH作用范围宽等，这使得海洋微生物在食品加工、酶工业、添加剂和医药等发酵行业具有极大的开发潜力和应用前景[1-5]。在海洋微生物发酵过程中，为保证发酵产物的品质和质量，需要实时检测一系列生物参数，尤其是基质浓度、菌体浓度及产物浓度(酶活)。当前，在线测量仪器仅能检测发酵过程中某些物理和化学参数，还没有成熟实用的仪器来测量这些关键生物参数[6-8]。在此背景下，许多关于微生物发酵过程中生物参数的软测量方法应运而生，其中，基于神经网络[9]的预测方法成为软测量领域的研究热点。然而，对于海洋微生物发酵过程这一类十分复杂的非线性系统来说，如果没有先验知识，就盲目应用神经网络方法，关键生物参数的测量问题就不能很好的解决。为此，文中将核主元分析法(Kernel Principal Component Analysis，KPCA)[10-12]和动态模糊神经网络(Dynamic Fuzzy Neural Network，D-FNN)[13-15]相结合，提出了一种基于KPCA-DFNN的软测量方法。

以典型的海洋微生物-海洋蛋白酶发酵过程为研究对象，首先，确定基质浓度、菌体浓度、相对酶活(能够更好地描述酶活的变化趋势)这三个参量为软测量模型的输出变量，环境变量为模型的初始输入变量。然后，利用KPCA对输入变量进行数据压缩和信息抽取，将所提取的主元作为DFNN的输入，以上三个变量作为DFNN的输出，建立了基于KPCA-DFNN的海洋蛋白酶发酵过程生物参量软测量模型。仿真结果表明，该模型较基于DFNN和PCA- DFNN建模具有学习速度快、预测精度高等优势，有益于海洋蛋白酶的高效、高质量生产。

1 核主元分析与动态模糊神经网络的原理

1.1 核主元分析

核主元分析是主元分析法(Principal Component Analysis，PCA)的非线性推广，其具体算法如下：

给定n个样本，样本集X={x1,x2,…,xn}，xk∈Rm，由非线性函数φ(·)将输入数据从原空间映射到高维特征空间F，F中的样本记为φ(xk)，且满足：

(1)

在F空间中样本的协方差矩阵C为

(2)

对C进行特征值分解

λV=CV

(3)

式中，V是与λ对应的特征向量，特征值λ≥0。将(3)式的两边左乘以核样本φ(xk)：

λφ(xk)·V=φ(xk)·CV，k=1,2,…,n

(4)

解方程可得与非零特征值对应的特征向量V。其解一定处于φ(x1),φ(x2),···,φ(xn)张成的空间中，所以V可以表示为：

(5)

其中，

φ(x)=[φ(x1),φ(x2),…,φ(xn)]，α表示a1,…,an中的一个列向量。

引入核函数：

Kij=K(xi,xj)=[φ(xi),φ(xj)],i,j=1,2,…,n

(6)

nλα=Kα

(7)

归一化特征向量V，即(V,V)=1，即可得样本x在特征空间中的第k(k=1,2,…,n)个主元分量tk(x)：

(8)

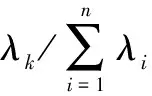
(9)

式(9)表示前p个λk的和与总和比值大于E，通常选取E>85%。

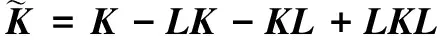
(10)

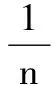
1.2 动态模糊神经网络

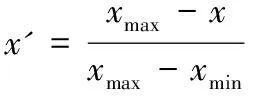
第1层：输入层，每个节点代表一个输入变量。

第2层：隶属函数层，每个节点代表一个隶属函数，该隶属函数可用式(11)表示：

(11)

其中，i=1,2,…,r,j=1,2,…,u，r是输入变量数，u是隶属函数的数量，即系统的总规则数，cij和σj分别是xi的第j个高斯隶属函数的中心和宽度，xmin是xi的第j个高斯隶属函数。

第3层：T-范数层，每个节点代表一个可能的模糊规则中的IF-部分，即该层的节点数反映了模糊规则数。第j个规则Rj的输出为：

(12)

其中：j=1,2,…,u，X=(x1,x2,...,xr)∈Rr，Cj=(c1j,...,crj)∈Rr是第j个RBF单元的中心。

第4层：归一化层，这些节点被称为N节点。其数目等于模糊规则的节点数。第j个节点Nj的输出为：

(13)

第5层：输出层，每个节点代表一个输出量，此输出是所有输入信号的叠加：

(14)

式中，wk是THEN-部分或者称为第k个规则的连接权，wk=ak0+ak1x1+…akrxr,k=1,2,…u，y是变量的输出。

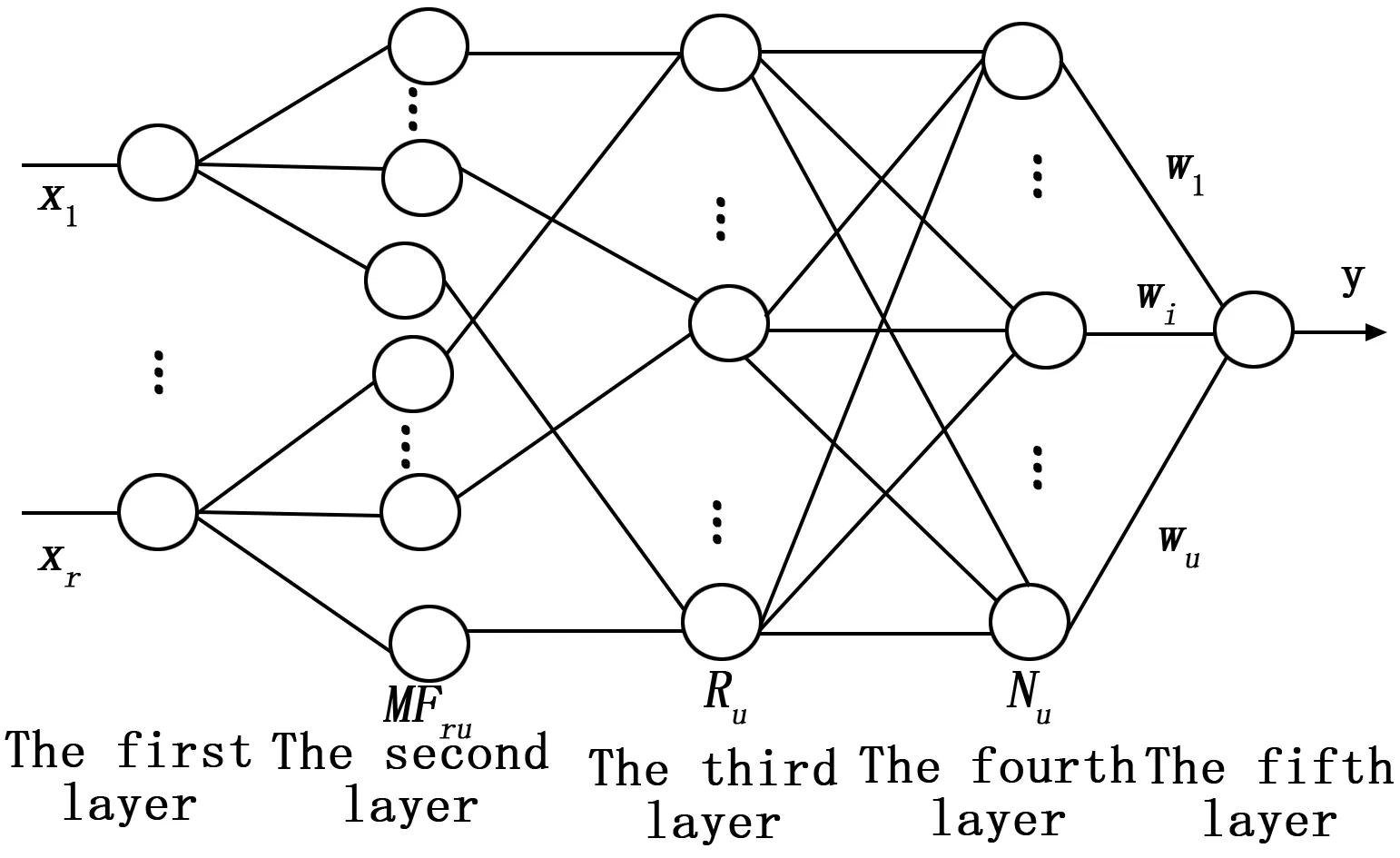
图1 DFNN的结构图

2 KPCA-DFNN模型的构建与验证

2.1 模型的构建

基质浓度S、菌体浓度X、相对酶活P对海洋蛋白酶发酵过程的优化控制非常重要，因此，选择这三个变量作为KPCA-DFNN软测量模型的输出变量。通过分析海洋蛋白酶发酵机理并结合发酵过程的实验数据，选取了10个影响生物参数S、X、P的主要因素作为初始样本变量，分别是：时间t、温度T、搅拌速度r、溶解氧浓度DO、空气流量l、pH值、CO2浓度、基质进给速率u、发酵罐压力p、反应器体积v。

采集了10批发酵数据，前9批作为模型的训练样本集，第10批作为模型的测试样本集，由于采集到的样本数据变化范围较大，如果直接使用原始测量数据进行计算，不仅会夸大量纲数据的作用，而且还可能导致信息丢失或引起数值计算的不稳定。需要对样本数据进行归一化处理。公式如下：

(15)

式中：xmax为样本数据的最大值，xmin为样本数据的最小值，x为原始样本数据，x′为归一化后的数据。归一化后样本数据在[0，1]之间。

根据核主元分析法和动态模糊神经网络的基本原理，构建了基于KPCA-DFNN的海洋蛋白酶发酵过程生物参量的软测量模型，建模过程如图2所示。建模步骤如下。

步骤1：根据建模对象选取适当的输入输出样本数据。

步骤2：利用式(15)对输入输出数据进行预处理。

步骤3：根据KPCA算法对输入变量进行数据压缩和信息抽取，消除输入变量之间的相关性，进行特征选取。文中按累积方差百分比大于95% ，KPCA选定了2 个特征主元，PCA选定了6个特征主元。

步骤4：将提取非线性主元作为DFNN的输入，X、S、P作为模型的输出变量，利用训练样本集对DFNN模型进行训练，选取最佳模型构建参数。

步骤5：利用测试样本集对建好的KPCA-DFNN软测量模型进行验证。

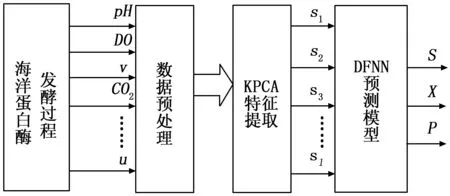
图2 海洋蛋白酶发酵过程预测模型框图

2.2 模型验证

用测试样本集对建好的KPCA-DFNN模型进行仿真验证。仿真结果如图3、图4和表2所示。

图3显示出了海洋蛋白酶发酵过程X、S、P的离线化验值(真实值)和软测量值(预测值)对比结果。

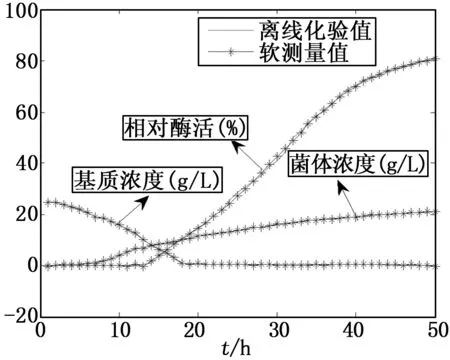
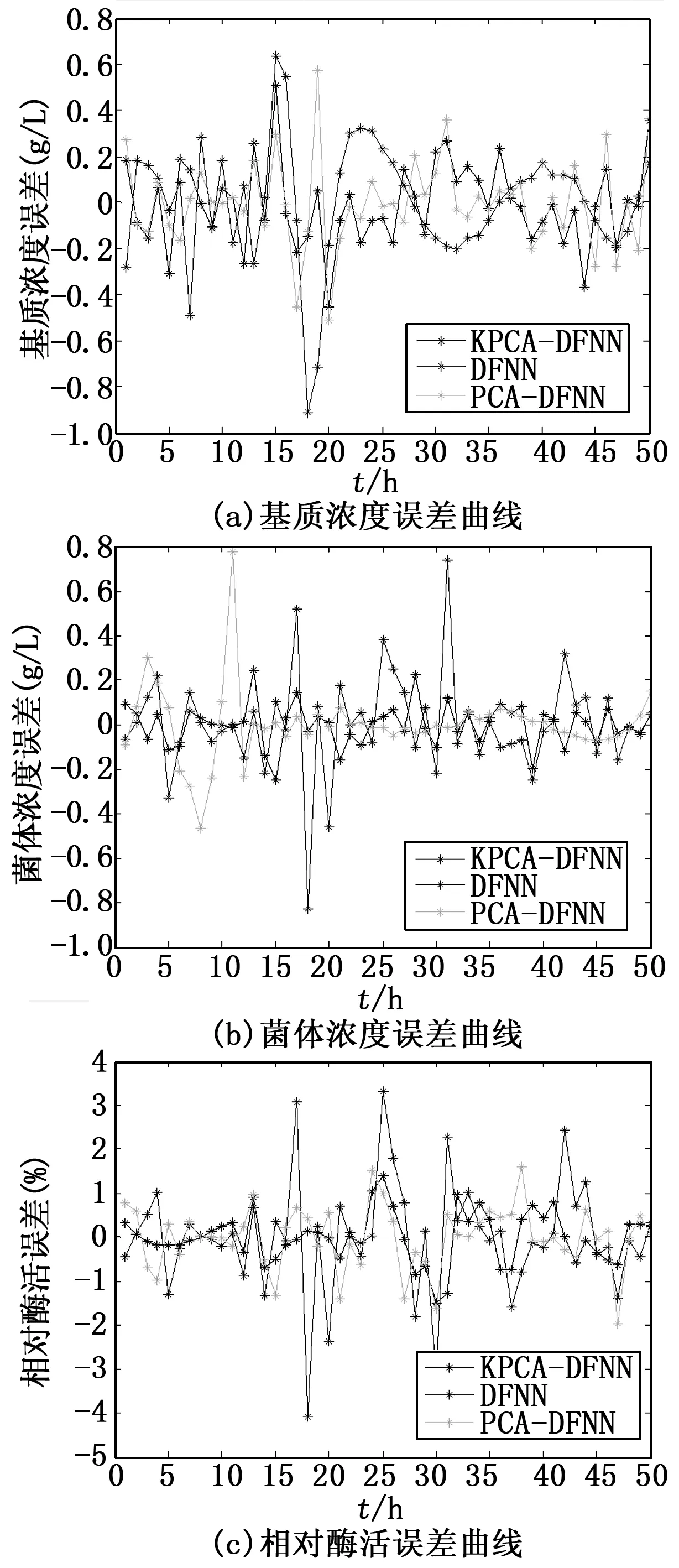
图3 KPCA-DFNN生物参量预测曲线

图4 DFNN、PCA-DFNN、KPCA-DFNN生物参量预测值误差曲线

虽然试验过程中采集到的样本值分散性很大和重复性很小，但从图3中可以看出，对于X、S、P，基于KPCA-DFNN的软测量模型，输出的软测量值都能够很好的追踪离线化验值，这说明，KPCA-DFNN具有较好的逼近能力。

采用均方根误差(RMSE)和平均绝对误差(MAD)更直观的反映DFNN、PCA-DFNN、KPCA-DFNN建模方式的预测效果，如表1所示。

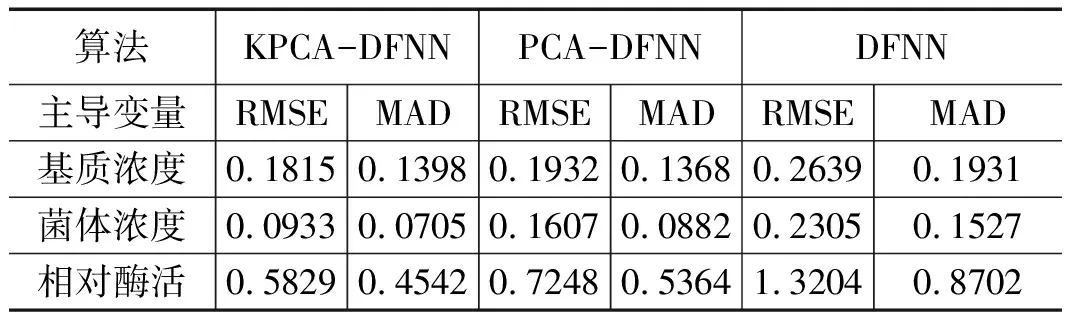
表1 DFNN、PCA-DFNN、KPCA-DFNN预测值误差对比

(16)

(17)

其中:n是数据对的数目，t(i)和y(i)是第i个期望输出与实际输出。

另外，为了更清晰地描述DFNN、PCA-DFNN、KPCA-DFNN的预测能力，图4中给出了这三种建模方法预测误差。

从表1和图4中可以看出，基于KPCA-DFNN的建模所得到基质浓度、菌体浓度和相对酶活的预测误差要比DFNN和PCA-DFNN小得多，这进一步表明，即使在同样的训练数据和测试数据的条件下，KPCA-DFNN的预测效果比DFNN和PCA-DFNN好。既基于KPCA-DFNN在发酵样本预测中具有显著的作用。

3 结论

为解决海洋微生物发酵过程中生物参量难以实时在线测量的问题，文中以海洋蛋白酶发酵过程为例，将核主元分析法(KPCA)与动态模糊神经网络(DFNN)相结合，提出一种基于KPCA-DFNN的建模方法。首先确定了X、S、P作为海洋蛋白酶预测模型的输出变量，同时，通过对海洋蛋白酶发酵过程进行机理分析，选定了10个影响输出变量的环境变量作为KPCA-DFNN模型的输入变量。用训练样本集对这些变量进行预处理后，按照累积方差百分比大于95%，KPCA提取了2 个特征主元。根据DFNN算法对提取后的数据进行学习训练，建立了基于KPCA-DFNN的海洋蛋白酶发酵过程生物参量的软测量模型，用测试样本集对模型进行仿真验证，试验结果表明与DFNN、PCA-DFNN建模方法相比，所建立的KPCA-DFNN模型具有良好的预测精度，所得生物参量预测值的最大RMSE为0.582 9，最大MAD为0.454 2，满足发酵过程中生物参量的在线测量要求。