超(超)临界火电机组乘数型协调预测函数优化控制研究及应用

胡建根, 孙 耘, 李 泉, 尹 峰

(国网浙江省电力公司电力科学研究院， 杭州 310014)

预测函数控制算法是于80年代中后期提出的第三代模型预测控制算法，其将控制输入的结构作为核心问题，可以克服其他模型预测控制中出现的规律不明的控制输入问题，具有快速响应能力和较强的鲁棒性[1-4]。

协调控制系统是现代单元机组控制的核心。目前，大型火电机组分为亚临界机组和超临界机组。亚临界机组是双输入双输出的多变量系统[5]，负荷的快速响应和压力的滞后响应构成一个耦合的矛盾体，对其很难进行有效控制[6]；超临界机组是三输入三输出的多变量系统[7-8]，负荷、压力与温度之间相互影响，耦合作用更为强烈，因此迫切需要一种优化解耦系统，对系统实现高效控制[9-11]。

笔者基于带有扰动的乘数型协调预测函数控制系统，提出了一种火电机组协调预测优化控制方法。对于亚临界机组，将预测函数控制系统应用于主汽压力控制回路，汽轮机调门指令作为预测系统的一种扰动信号进行控制，可以较好地解决系统耦合问题。对于超临界机组，将预测函数控制系统应用于主汽压力控制回路，汽轮机调门指令和给煤量指令作为预测系统的一种扰动信号进行控制，计算出给水优化指令，叠加前馈信号后作用于整个系统；将预测函数控制系统应用于过热汽温控制回路，给水量指令作为预测系统的一种扰动信号进行控制，计算出给煤量优化指令，叠加前馈信号后作用于整个系统，有效地解决了系统的耦合问题。该控制算法简单、易于工程实现，具有较强的实用价值。

1 乘数型预测函数控制原理

预测函数控制算法包括预测模型、滚动优化和反馈校正3部分[12]。

1.1 预测模型

预测模型输出ym(k)由2部分组成：一部分是过去时刻的控制量及输出量，另一部分是当前时刻及未来时刻的控制量和输出量。过去时刻的响应输出可表示为y1(k)，当前时刻及未来时刻的响应输出可表示为yf(k)，则预测函数的模型输出可表示为ym(k)=y1(k)+yf(k)。

在预测函数控制中，新加入的控制作用可以表示为若干已知函数的线性组合：

(1)

式中：k为时刻；N为控制时域；μn为线性组合系数；fn为基函数；H为预测时域。

加入该控制作用后响应输出为：

(2)

式中：gn(i)为在fn(i)作用下的模型输出，可离线计算得出。

1.2 滚动优化

预测控制优化是在有限时域内的动态优化，参考轨迹yr采用一阶指数形式：

yr(k+i)=(1-βi)×c(k+i)+βi×y(k)

(3)

式中：c为设定值；β为系数；y(k)为过程输出。

滚动优化时采用的性能指标如下：

(4)

yp(k+i)=ym(k+i)+e(k+i)

式中：P1、P2为优化时域的下限和上限；yp(k+i)为过程预测输出；ym(k+i)为模型输出；e(k+i)为未来误差。

1.3 反馈校正

在实际工况中，由于模型失配、参数时变及噪声等影响，预测输出与实际输出存在偏差，因此未来误差可表示为：

e(k+i)=y(k)-ym(k)

(5)

1.4 最优控制律

预测模型选为一阶加迟延对象：

(6)

式中：Km为模型增益；Tm为模型惯性时间；Td为模型延迟时间。

采用阶跃函数时：

u(k+i)=u(k),i=1,2,…,H-1

(7)

当系统无纯迟延时，通过对优化指标式(4)求偏导数可以获得最优控制律；当系统有迟延时，采样周期为Ts，设D=Td/Ts，则经修正后的模型输出为

ypav(k)=y(k)+ym(k)-ym(k-D)

(8)

最优控制律可表达如下：

(9)

式中：αm=e-(Ts/Tm)。

1.5 乘数型预测函数最优控制律

笔者提出了一种乘数型预测函数控制方法，将式(9)中的最优控制律改为：

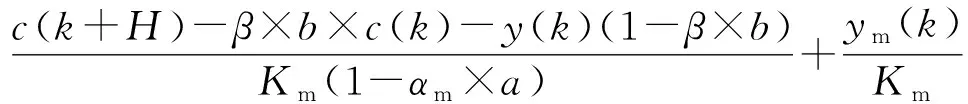
(10)

式中：b为参考轨迹预测调整系数；a为控制预测调整系数。

在调整控制系统品质时，只需调整预测调整系数a和b，便可获得良好的控制品质。根据仿真经验，a和b的取值范围为a>1.1，b>1.4。a和b取值不同对调节品质的影响规律为：当a过大时，系统响应变慢但鲁棒性增强，当a过小时，系统响应变快但鲁棒性较差；当b过大时，系统响应变快但会出现震荡或不稳定现象，当b过小时系统响应变慢。

1.6 带扰动信号的预测函数最优控制律

当控制系统的外部扰动信号可测时，可以通过试验确定系统的扰动模型，此时系统具有2个模型，即控制通道模型Gm1(s)和扰动通道模型Gm2(s)，假定二者均为一阶加迟延模型：

(11)

(12)

当采用一个基函数时：

(13)

各通道的预测输出为：

(14)

其中,αm1=e-(Ts/Tm1),αm2=e-(Ts/Tm2)。

预测模型输出为：

ym(k+H)=ym1(k+H)+ym2(k+H)

(15)

根据优化指标的极值可以获得最优控制律为：

(16)

1.7 带扰动信号的乘数型预测函数最优控制律

按照式(10)的方法将式(16)设计成乘数型预测函数最优控制律：

u(k)=

(17)

2 超临界机组协调预测函数优化控制

2.1 超临界机组特性分析

超临界机组是三输入三输出的多变量控制系统，在锅炉燃烧、给水和发电机励磁系统均正常工作的前提下，锅炉、汽轮机系统可在给定的工况下简化为一个具有强耦合的三输入三输出系统：

(18)

式中：ΔN为机组功率变化量；Δp为主汽压力变化量；ΔT为机组过热度变化量；Δμ为汽轮机调门开度变化量；ΔB为给煤量变化量；ΔW为给水变化量。

根据试验可以确定式(18)中各函数的形式，其中G11可近似为微分环节，G12、G13、G21、G22、G23、G32和G33可近似为惯性加迟延环节，G31为调门对过热度的特性函数，其对过热度的影响较小可忽略。

由上述分析可知，超临界机组的特性函数中包含了大部分的惯性加迟延环节[13-14]。利用预测函数控制系统特有的解耦能力来实现协调控制的解耦，解决压力和温度等带有惯性加迟延对象的控制难题，得到高品质的控制性能。

2.2 超临界机组协调预测函数优化控制原理

针对超临界机组特性函数设计的预测函数控制系统如图1所示[15]。其中，Gtm2、Gbm2、Gfm1分别为调门、给煤量和给水对主蒸汽压力的对象特性函数模型；Gm2、Gm1为给水、给煤量对分离器出口过热温度的对象特性函数模型；PFC1为主汽压力预测函数控制器，控制量u1为优化给水量；PFC2为过热温度预测函数控制器，控制量u2为优化给煤量。

锅炉主控指令经u1的反算函数f1(x)计算出对应给煤量，与基准给煤量f2(x)、前馈给煤量ff以及优化给煤量u2叠加后获得总给煤量指令Bu；给水量指令fw则由基准给煤量f2(x)和前馈给煤量ff之和经惯性环节后，叠加优化给水量u1获得；汽轮机调门指令Tu则由负荷偏差经控制器PID1后计算获得。

汽轮机调门指令与给煤量指令作为整个压力控制回路的扰动信号源，主通道为给水对压力的函数模型，按照第1.7节所述方法可以推导出主汽压力预测函数的最优控制律。当控制系统的外部扰动信号Tu、Bu可测时，系统具有控制通道Gfm1(s)和扰动通道Gbm2(s)、Gtm2(s) 3个模型，均简化为一阶惯性加纯迟延模型后可得：

(19)

(20)

(21)

图1 预测函数在超临界机组协调控制中的应用Fig.1 Application of predictive functions in coordinated control of supercritical units

当采用一个基函数时，有：

(22)

各通道的预测输出为：

(23)

式中:αfm1=e-(Ts/Tfm1)，αbm2=e-(Ts/Tbm2)，αtm2=e-(Ts/Ttm2)。

预测模型输出为：

ypm(k+H)=yfm1(k+H)+ybm2(k+H) +

ytm2(k+H)

(24)

按照乘数型预测函数设计方法可获得最优控制律：

u2(k)=[c2(k+H)-β×b×c2(k)-(1-β×b)×

y1(k)-αfm1×a×yfm1(k)-αbm2×a×

ybm2(k)-αtm2×a×ytm2(k)-Kbm2×1-

αbm2×a×Bu(k)-Ktm2(1-αtm2×a)×

Tu(k)+ypm(k)]/[Kfm1×(1-αfm1×a)]

(25)

式中：c2(k+H)为第k+H时刻的设定值。

给水量指令作为整个温度控制回路的扰动信号源，主通道为给煤量对温度的函数模型，同样推导出过热温度控制的最优控制律。当控制系统的外部扰动信号fw可测时，系统具有控制通道Gm1(s)和扰动通道Gm2(s) 2个模型，均简化为一阶惯性加纯迟延模型后可得式(11)和式(12)。

当采用一个基函数时：

(26)

各通道的预测输出为：

(27)

预测模型输出为：

ym(k+H)=ym1(k+H)+ym2(k+H)

(28)

按照乘数型预测函数设计方法可以获得最优控制律为：

u(k)=[c2(k+H)-β×b×c2(k)-(1-β×b)×

y2(k)-αm1×a×ym1(k)-αm2×a×ym2(k)-

Km2×1-αm2×a×fw(k)+ym(k)]/

[Km1×(1-αm1×a)]

(29)

2.3 1 000 MW超超临界火电机组协调预测函数优化控制

某厂1 000 MW超超临界火电机组中，锅炉型号为SG-3091/27.56-M54X，超超临界、一次中间再热、固态排渣、平衡通风、四角切圆燃烧、露天布置及全钢结构的直流锅炉；汽轮机为中间再热凝汽式汽轮机组，额定功率为1 000 MW；发电机型号QSFN-1000-2,为水氢氢冷却汽轮发电机组。

经拟合简化，得到以下一阶惯性加纯迟延对象模型：

给煤量对压力的预测模型

(30)

调门对压力的预测模型

(31)

给水对压力的预测模型

(32)

给水对温度的预测模型

(33)

给煤量对温度的预测模型

(34)

主汽压力控制器PFC1的3个预测模型分别取：Kfm1=0.002 5，Tfm1=60，Tfd1=30；Kbm2=0.019，Tbm2=150，Tbd2=300；Ktm2=-0.035，Ttm2=45，Ttd2=60；过热温度控制器PFC2的2个预测模型分别取：Km1=0.5，Tm1=150，Td1=260；Km2=-0.063，Tm2=45，Td2=80。

进行控制系统负荷变动试验，将变负荷速率设置为10 MW/min，负荷指令变化100 MW时获得的响应曲线见图2和图3。

由图2和图3可知，负荷控制偏差在±10 MW，压力控制偏差在±0.5 MPa，过热度控制偏差在±5 K，控制性能优良。

为了更好地验证该算法的有效性，当机组处于自动发电控制(AGC)状态时，分别采用本优化算法和常规控制策略进行控制响应对比。当机组由830 MW变化至610 MW时，机组的AGC响应曲线见图4和图5。

图2 协调预测控制负荷和压力响应曲线Fig.2 Load and pressure response in coordinated predictive control

图3 协调预测控制过热度响应曲线Fig.3 Degree of superheat response in coordinated predictive control

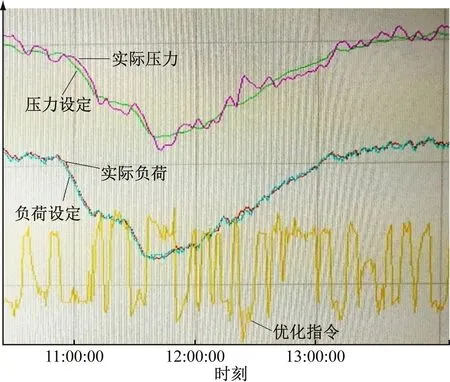
图4 优化控制策略AGC响应曲线Fig.4 AGC response curve based on optimized control strategy

由图4和图5可知，优化控制算法中机组AGC响应负荷控制偏差在±8 MW，压力控制偏差在±0.5 MPa，中间实际负荷始终能快速跟踪指令，提高了机组的AGC控制性能。常规控制算法中机组AGC响应负荷控制偏差在±13 MW，压力控制偏差在±1 MPa，中间负荷响应长时间存在一定的偏差，机组的AGC控制性能受到限制。

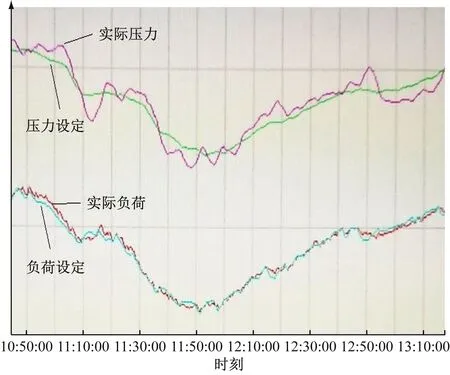
图5 常规控制策略AGC响应曲线Fig.5 AGC response curve based on conventional control strategy

3 结 论

提出了一种乘数型预测函数控制方法，设计了带扰动信号的乘数型预测函数最优控制律，并将其应用于超超临界机组主汽压力与过热汽温控制回路。根据超超临界机组的对象特性，设计了具体的控制结构，推导出相应的优化控制律，较好地解决了协调控制系统中的耦合问题。通过对超超临界机组的工程应用，证明了该算法在机组变负荷过程中，能够保证负荷控制偏差在±10 MW，压力控制偏差在±0.5 MPa，过热温度控制偏差在±5 K；在机组AGC运行时，协调预测控制系统较常规协调控制系统负荷控制精度提高30%以上，压力波动幅度减少40%以上。同时算法简单、易于工程实现，具有良好的应用前景。