考虑SSI效应的风力机塔架地震动力响应时频特性分析

刘中胜， 杨 阳， 李 春,2， 邹锦华

(1. 上海理工大学 能源与动力工程学院， 上海 200093；2. 上海市动力工程多相流动与传热重点实验室， 上海 200093)

我国风能资源的整体特点是分布广、不稳定和能量密度相对较低[1]。风能资源丰富的东南沿海和“三北”地区均位于地震多发地带，这些区域的风场风力机极易受到地震载荷的影响。地震具有很强的不可预见性和突发性，结合国内外风力机结构抗震设计的理论研究和工程应用需求，风力机系统结构地震动力响应特性分析已成为当前亟待解决的重要课题[2]。随着风力机的大型化发展，在时域非定常和空间非均匀的湍流风中叶片与塔架等细长柔性弹性体结构气动弹性的非线性现象十分明显[3-4]。此外，如果同时受到地震载荷的激励作用，很可能导致风力机塔顶振动失稳和塔基结构被破坏[5]。因此，对于提高风力机结构精细化设计和系统运行可靠性控制来说，研究大型风力机塔架在风-震耦合工况下的动力响应具有重要意义。关于地震激励下风力机塔架的动力特性，国内外学者进行了大量的相关研究。根据随机地震动物理模型可生成加速度,贺广零等[6]建立了风力机“桨叶-塔体-基础”一体化有限元模型，发现土-构耦合(SSI)效应会在一定程度上增大结构响应幅值。贺广零[7]建立了SSI模型，通过确定弹簧振子的刚度模拟出塔基处的地震载荷，发现SSI效应会增加塔基与地基连接的柔度，影响塔架的振型和振动频率。周勃等[8]基于有限元分析方法研究了风力发电机塔架的动力特性和影响因素，确定了结构的有限元模型和划分网格的方法。祝磊等[9]采用Ansys有限元软件的Beam188单元建模，运用时程分析法研究不同强度地震激励下风力机结构的非线性动力响应规律。Nuta等[10]在不同载荷作用下对风力机结构的动力特性进行了较为详细的分析，确定了结构的破坏位置及破坏形式，从而有效地进行加强与检测，以保证风力机的结构安全。Bazeos等[11]建立了风力机塔架壳体模型，分析地震载荷对风力机结构动力响应的影响，并初步考虑了土-构相互作用的影响。Tanabe等[12]对600 kW风力机进行了动力分析，发现在罕遇地震激励下塔体的弯矩超过了初始弯矩。Lavassas等[13]基于有限元法计算出风力机钢制圆柱型塔架在地震载荷作用下的结构强度。

以上研究均简化甚至忽视了风载荷对风力机结构强度的影响。而实际上随着风力机的大型化发展，风载荷效应明显增大，气动载荷对风力机结构的影响不可忽视。对于现代大型化风力机的动力学仿真模拟来说，研究表明地震载荷和气动载荷的耦合作用对风力机整机动力学特性的影响非常重要[14-15]。

笔者以美国可再生能源实验室(NREL)的5 MW风力机[16]为计算样机，基于Wolf方法[17]建立了SSI模型，综合考虑了结构的非线性特性和不同场地土质对地震动的放大效果，研究风力机塔架在不同地震动作用下的时频特性，为风力机结构抗震设计提供了理论参考。

1 仿真模型及参数

1.1 研究对象

采用NREL的5 MW风力机[16]作为研究对象，其主要参数见表1。

表1 NREL 5 MW风力机主要参数Tab.1 Main parameters of the NREL 5 MW wind turbine

1.2 风力机坐标系

笔者主要研究在不同场地土质下地震对风力机塔架动力响应的影响。为方便计算，在风力机上建立2个相对坐标系，分别为地基坐标系{o,x,y,z}和塔顶坐标系{o′,x′,y′,z′}，风力机模型及结构计算坐标系的自由度如图1所示。

图1 风力机模型及计算坐标系Fig.1 Model and coordinate system of the wind turbine

1.3 地震动仿真模型

基于Wolf方法建立风力机基础平台与土地间的耦合作用模型。将地震载荷与结构振动的耦合作用等效为弹簧振子，通过定义弹簧振子的阻尼和刚度，即可将地震运动转化为相应的地震载荷，SSI模型如图2所示。

各个方向的阻尼C和刚度K通过式(1)和式(2)进行计算。

(1)

(2)

式中：Kx和Ky分别为纵向和横向的刚度；Kz为垂向的刚度；Cx和Cy分别为纵向和横向的阻尼；Cz为垂向的阻尼；Gs、μs和ρs分别为土体的切变模量、泊松比和密度；Rs为基础平台的半径。

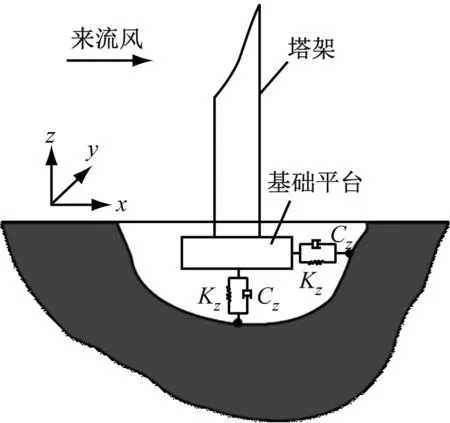
图2 SSI模型Fig.2 SSI model of the wind turbine platform

1.4 仿真流程

风场仿真软件、地震和动力学模拟软件均采用NREL的计算机辅助设计包软件。基于风力机多体动力学仿真开源软件Fast，通过子模块TurbSim、AeroDyn和Sesimic建立风力机地震动力学仿真模型，具体步骤如图3所示。

2 塔架外部激励

2.1 气动载荷

在y″和z″方向上风场设计计算各有11个网格点，风场示意图如图4所示。

额定风速为11.4 m/s，极限风速为25 m/s(切出风速)，通过TurbSim[18]模拟风力机的运行环境。通过经典Von Karman湍流风谱模型对功率谱进行逆快速傅里叶变换，继而得到风速的波动。Von Karman湍流风谱模型定义为[19]：

(3)

图3 地震动力学仿真流程Fig.3 Flow chart of seismic dynamics simulation

图4 风场计算区域及网格分布Fig.4 Computational domain and grid distribution of the wind field

(4)

塔架某一高度h处风作用于塔架产生的气动载荷可表示为[20]：

(5)

式中：H为塔架高度；V(h)为高度h处的风速；D(h)为高度h处塔架的外径；C(h)为阻力系数；δ为阵风因子。

通过TurbSim模拟u、v和w这3个方向的风速，基于Matlab的数据处理和绘图功能，计算得到湍流风场风速变化，如图5所示。

图5 风场风速变化Fig.5 Wind speed distribution in the wind field

2.2 地震反应谱及地震载荷

地震载荷以加速度的形式作用于风力机塔架基底[21]，根据抗震设计规范定义的反应谱生成加速度。图6为根据GB 50011—2010 《建筑抗震设计规范》[22]定义的标准地震反应谱，其中αmax为地面设计加速度的峰值；γ为衰减系数；η1为直线下降段的斜率调整系数；Tg为特征周期；η2为阻尼调整系数；T为结构自振周期。

图6 地震反应谱示意图Fig.6 Schematic diagram of the response spectrum

当结构阻尼比ξ不为5%时，地震影响系数曲线的阻尼修正系数和形状参数应符合标准规定。

曲线下降段的衰减系数γ按下式确定：

(6)

直线下降段的斜率调整系数η1(当η1小于0时取0)按下式确定：

(7)

阻尼调整系数η2(当η2小于0.55时取0.55)按下式确定：

(8)

式中：ξ为结构阻尼比，取ξ=5%。

我国幅员辽阔，区域土质差异性较大。其中，东南沿海地区以软土为主；硬黏土主要分布在南方，以贵州和云南最为典型；岩土主要分布在广西[23]。笔者研究场地为软土、硬黏土和岩土3种不同土质时风力机结构的动力响应，3种土质对应的物性参数[24]如表2所示。

表2 3种不同土质的物性参数Tab.2 Physical properties of three different soils

参考GB 50011—2010 《建筑抗震设计规范》[22]，根据场地条件和风力机结构抗震强度要求，选取合适的特征周期Tg和地面设计加速度峰值αmax，如表3和表4所示。

表3 特征周期取值Tab.3 Characteristic period values

表4 地面设计加速度峰值Tab.4 Design values of maximum ground acceleration

风力机抗震设防烈度为8度、场地土质为软土时对地震设计加速度反应谱进行模拟[25]，可得到人工合成的地震加速度，如图7所示。对已获得的人工合成地震加速度进行谱分析，可回归为拟合的设计加速度反应谱(匹配谱)，并与目标谱进行比较，如图8所示。

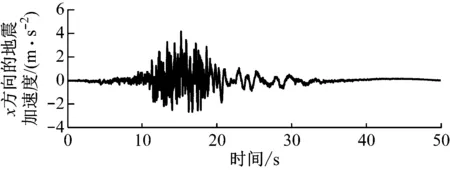
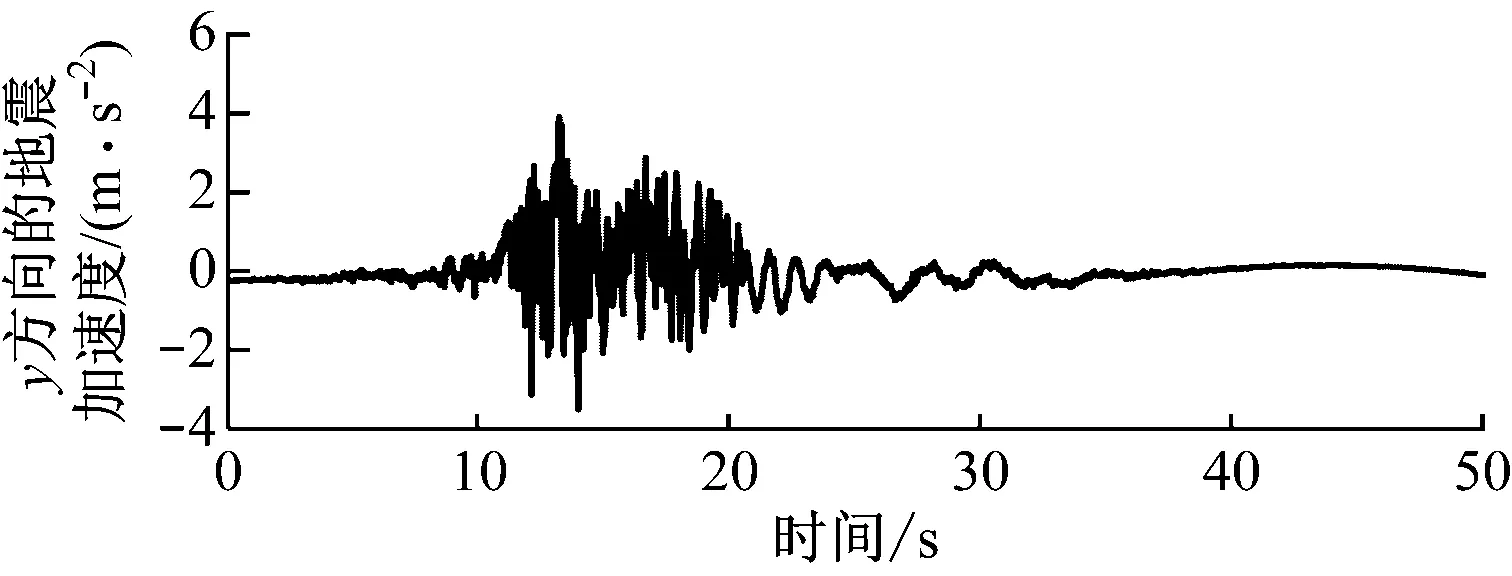
图7 人工合成的地震加速度Fig.7 Acceleration of simulated earthquakes

由图8可知，目标谱和匹配谱的误差很小，最大误差不超过10%，绝大部分的误差在2%左右。这表明匹配谱与目标谱的吻合较好，证明人工合成地震的有效性和科学性。

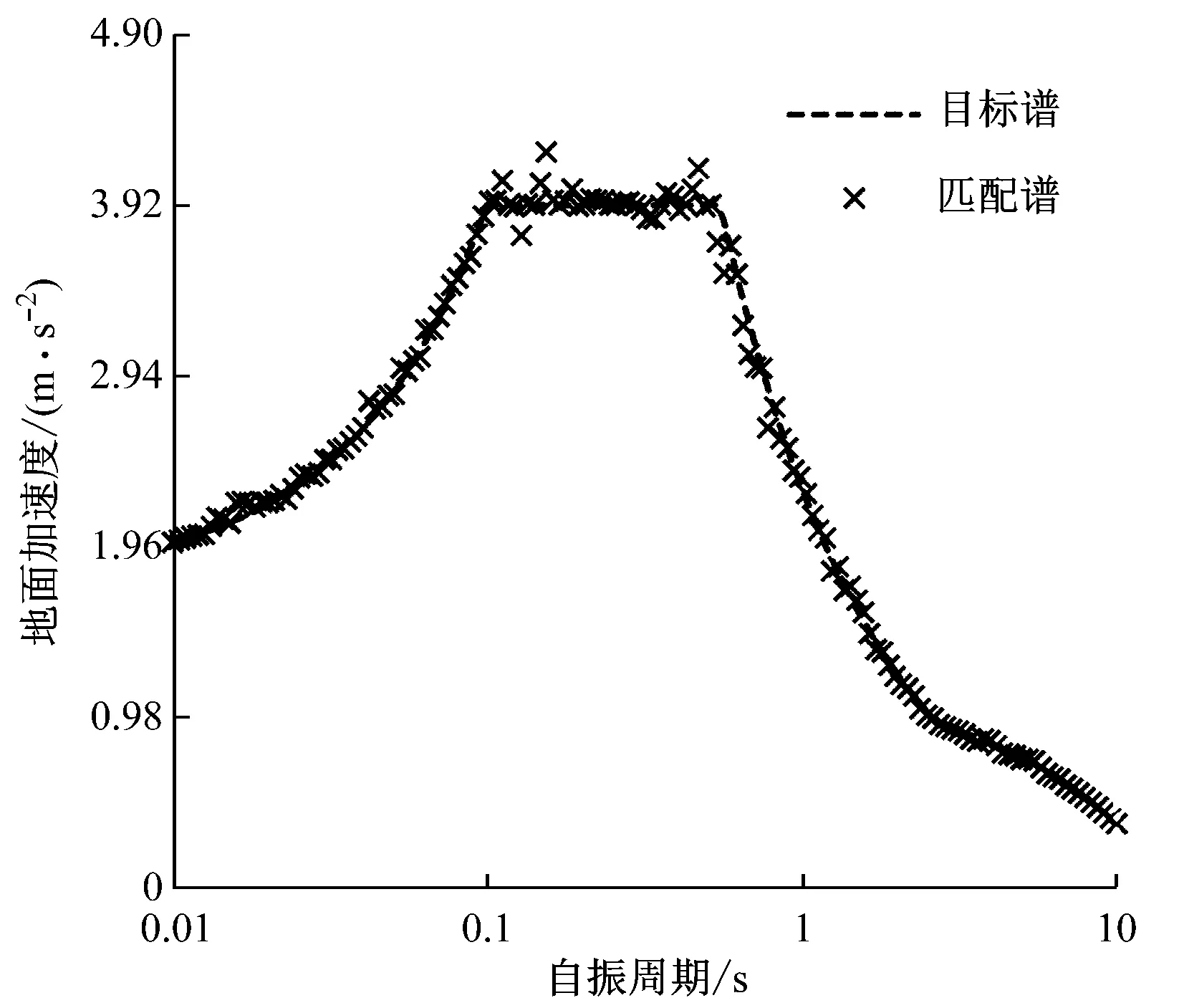
图8 匹配谱和目标谱的比较Fig.8 Comparison between matching and target spectrum

3 结果与分析

风力机在正常工况下运行，每个算例的仿真时间为600 s，时间步长为0.002 s，在400 s时加入地震，持续时间为50 s。

3.1 时域分析

采用时域分析法研究不同工况下风力机塔架的动力响应，图9给出了当风-震耦合作用、风单独作用与地震单独作用时风力机塔顶侧向位移的变化曲线。

由图9可知，在地震激励及不同场地土质下塔顶侧向位移曲线的变化趋势基本一致，但响应幅值存在差异。由图9(a)可知，在风-震耦合作用下，当场地为软土、硬黏土和岩土时塔顶侧向位移最大值分别为0.360 m、0.409 m和0.337 m。由图9(b)可知，在额定风速和极限风速下塔顶侧向位移最大值分别为0.098 4 m和0.245 m。由图9(c)可知，地震强度为8度时，当场地为软土、硬黏土和岩土时塔顶侧向位移最大值分别为0.368 m、0.344 m和0.310 m，场地为软土时塔顶侧向位移最大，场地为岩土时能量耗散速率和塔顶侧向位移减小速度较慢。对比图9(b)和图9(c)可知，地震对塔顶侧向位移的影响很大，与无地震时相比，在额定风速下发生地震时软土、硬黏土和岩土塔顶侧向位移最大值分别增大265%、316%和242%，在极限风速下分别增大47%、67%和38%。

图10为不同工况下风力机塔基弯矩的变化。由图10可知，在风-震耦合作用及不同土质的情况下塔基弯矩曲线的变化规律比较复杂。风力机在额定风速下气动载荷最大。在极限风速下叶轮变桨导致气动载荷减小，故塔基弯矩(最大值为66.3 MN·m)小于额定风速下的塔基弯矩(最大值为87.4 MN·m)。当场地为不同土质时塔基弯矩的最大值基本相同，均在65 MN·m左右。地震结束后(>450 s)，场地为岩土时能量耗散速率最慢，塔基弯矩降低速度也最慢。对比图10(b)和图10(c)可知，地震载荷对塔基弯矩的影响与气动载荷相当，处于同一数量级。

地震加速度转化为地震载荷作用于平台底部，使其产生一定的加速度，场地为不同土质时平台加速度如图11所示。由图11可知，地震载荷对平台加速度的影响很大。无地震时，即在额定风速下平台加速度始终为0 m·s-2，即平台仅受地震载荷的影响。由于软土阻尼较小，平台自由度相对较大，在相同的地震激励下平台的动力响应更为剧烈。

(a) 风-震耦合作用

(b) 风单独作用

(c) 地震单独作用图9 不同工况下塔顶侧向位移的变化Fig.9 Time domain variation of lateral displacement of tower top under different working conditions

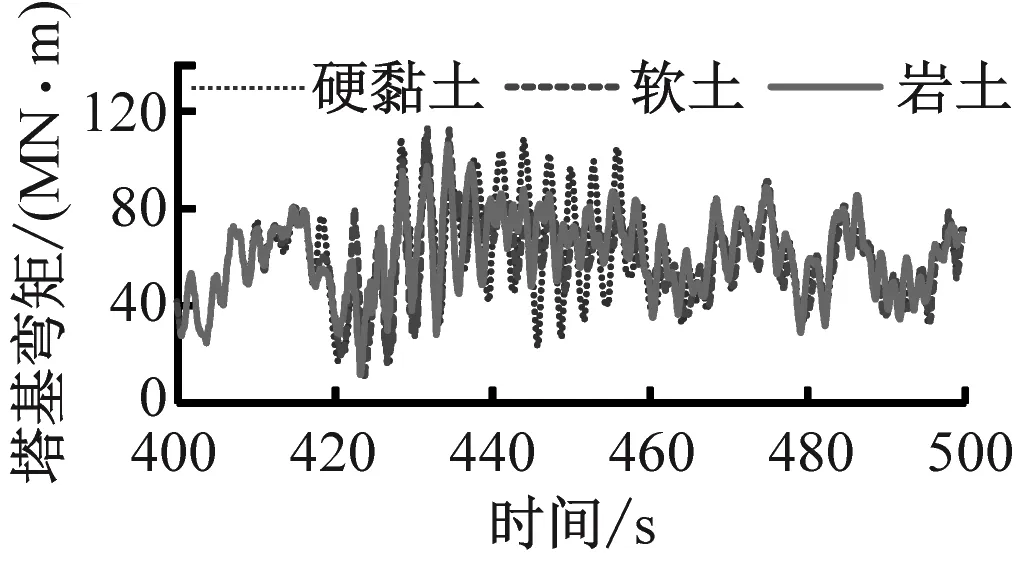
(a) 风-震耦合作用

(b) 风单独作用

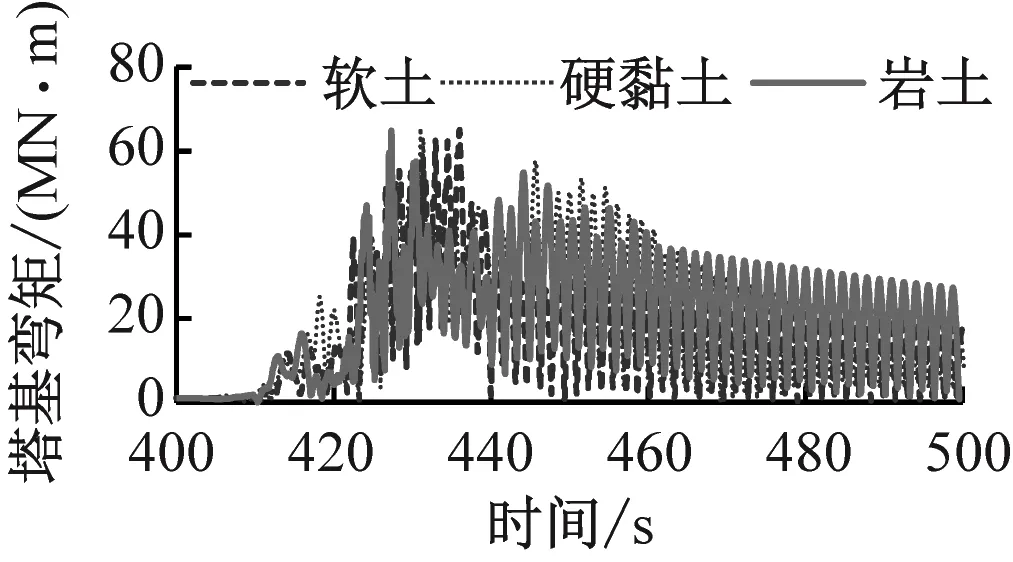
(c) 地震单独作用图10 不同工况下塔基弯矩的变化Fig.10 Time domain variation of bending moment of tower base under different working conditions

(a) 平台前后加速度

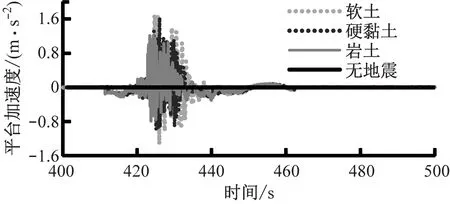
(b) 平台侧向加速度图11 不同土质时风力机平台加速度的变化

Fig.11 Time domain variation of platform acceleration for the tower in different soils

3.2 频域分析

由于塔顶响应是风载荷、地震载荷等随机载荷共同作用的结果，需通过频域分析进一步研究塔架的振动特性。通过对400～500 s内塔顶的响应进行快速傅里叶变换(FFT)，对应的塔顶位移频域动力响应如图12所示。

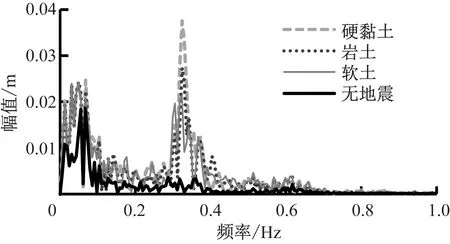
(a) 塔顶前后位移

(b) 塔顶侧向位移图12 塔顶位移频域动力响应

Fig.12 Dynamic response of tower top displacement in frequency domain

由图12可以看出，无地震时塔顶振动尤其是塔顶侧向振动不明显。地震发生后，地震载荷使得塔架一阶固有频率(0.32 Hz)处的振动急剧增大。由此可知，地震是导致塔顶振动的主要因素，尤其是对塔顶侧向振动的影响远大于气动载荷的影响。

4 结 论

(1) 在额定风速下，设防烈度为8度时，地震载荷对塔顶位移和塔基弯矩的影响不可忽视，尤其是对塔顶侧向位移的影响远大于气动载荷；在极限风速下，地震载荷对塔顶侧向位移的影响略大于气动载荷。

(2) 地震载荷极大加剧了塔顶尤其是塔架一阶固有频率处的振动。设防烈度为8度时，塔顶振动主要激励为地震载荷，气动载荷对塔顶侧向振动的影响较小。进行塔架结构抗震设计时，应充分考虑地震载荷的影响。

(3) 当场地为不同土质时，由于阻尼不同，塔架自由度及能量耗散速率不同，塔架时频特性差异性较大。在风-震耦合工况下，与软土和岩土相比，场地为硬黏土时塔架响应幅值和振动更大，故场地为硬黏土时风力机的结构抗震设计更应考虑SSI的影响。