自发射流耦合凹槽抑制涡轮叶尖泄漏的数值研究

胡建军, 张香兰， 张 铎， 孔祥东

(1.燕山大学 机械工程学院，河北秦皇岛 066004； 2. 燕山大学 建筑工程与力学学院，河北秦皇岛 066004)

涡轮叶顶间隙的存在影响了涡轮性能，可造成涡轮中三分之一以上的流动损失，因此积极发展叶尖泄漏抑制技术尤为重要。常见的间隙泄漏抑制方法是改变叶顶局部结构。张军等[1]和Lee等[2]分别研究了叶顶装吸力面肋条和压力面肋条对叶栅气动性能的影响，结果表明吸力面加装肋条会导致泄漏量增大，且肋条越低，泄漏量越大；随着压力面肋条高度的增加，流向切面的总压损失系数先急剧减小后逐渐增大。李伟等[3]提出在压力面和吸力面均设置肋条(即凹槽)抑制叶尖泄漏，发现适当的肋条参数可减小泄漏损失，提高涡轮效率。肋条高度对涡轮效率有较大影响，且存在最佳肋条高度，而肋条宽度对流场的影响不大。

Kang等[4]进一步研究发现，随着凹槽深度增加，凹槽内的平均传热/传质速率和间隙泄漏量先大幅减小后趋于平缓，且在平均传热/传质速率方面，凹槽深度比间隙高度更敏感。叶学民等[5-6]研究了凹槽状叶顶的传热特性以及凹槽形态对轴流风机性能和动叶气动性能的影响。此外，叶学民等[7]研究了叶顶双凹槽对轴流风机气动性能和振动特性的影响，结果表明在叶顶加装双凹槽后，间隙泄漏量显著减小，且减小幅度随开槽深度的增加而趋缓。

近期出现了一种叶尖泄漏气动封严方法，即在叶尖间隙引入反方向气流来阻挡间隙来流。根据引入气流驱动方式不同，可以分成主动射流和被动射流2种。其中，主动射流通过外部能量驱动供气，Rao等[8-9]通过实验和数值模拟考察了主动射流的开孔位置和射流量等对泄漏流动的影响。Abdulrahim等[10]研究了主动射流对风机气动性能的影响，结果表明主动射流能有效控制间隙流动，提高风机效率。而Gao等[11]则提出将凹槽与叶尖主动射流耦合抑制叶尖泄漏，结果表明主动射流可较好地控制叶尖泄漏量，而凹槽又能使叶尖获得更好的冷却，采用复合方法控制叶尖泄漏量存在一定优势。

被动射流不需要额外引气装置，结构简单，实现便利，因此一直受到研究者的青睐。Auxier[12]最早提出利用叶片自然压差生成一股气流控制叶尖泄漏量的思想。2007年，Hamik等[13]提出一种具体的开孔方案并进行了初步的理论分析。曹传军等[14]提出在某毫米尺度涡轮应用被动式叶尖逆向涡流发生器以减小叶尖泄漏量，在典型进口条件下，加装逆向涡流发生器使得叶尖泄漏量减小了3.3%。笔者运用实验和数值方法研究了自发射流对叶尖泄漏的影响，发现叶尖射流的引入在泄漏流抑制方面可取得一定的收益，在典型工况下，引入叶尖自发射流后可将泄漏比(即叶尖泄漏量与叶栅进口质量流量之比)降低5.42%[15-16]。

目前，采用单一控制方法抑制叶尖泄漏的潜力已接近极限。笔者考虑将被动射流与叶尖几何改型相结合，提出一种复合被动控制方法——自发射流耦合叶顶凹槽，用于抑制叶尖泄漏及其损失。首先，通过抽象简化得到耦合结构的数值计算模型，运用正交试验法优化自发射流参数，并筛选出与之匹配的复合被动组合方案，进行了详细的数值研究，最终获得了比单一控制方法更优的泄漏抑制效果。

1 数值计算模型

所采用的基础叶栅模型为具有详细几何尺寸和试验数据的Durham平面叶栅，具体参数见表1。

表1 叶珊主要参数Tab.1 Main parameters of the cascade

笔者主要考察自发射流耦合叶顶凹槽对叶尖泄漏的抑制效果，暂不考虑泄漏流动对通道主流的影响，因此只在叶片前缘截取了弦长为100 mm且带有4个自发射流孔道的部分作为数值计算模型，如图1所示。

1.1 几何建模及网格划分

叶栅计算模型的几何建模由SolidWorks软件完成，计算域如图1所示，其中X方向为轴向，Y方向为叶片展向，Z方向为周向。网格划分采用Gambit软件，采用分块结构化网格进行整体网格划分，在近壁面区进行网格加密，射流孔附近网格划分细节如图2所示。

图1 叶尖自发射流与凹槽耦合模型Fig.1 Model of spontaneous tip injection coupled with tip squealer

图2 数值计算模型网格Fig.2 Meshing of computational model

为了考察计算结果对网格数的依赖性，选取了6套逐渐加密的网格模型进行计算。由于主要考察自发射流耦合叶顶凹槽对叶尖泄漏流动的抑制作用，因此根据实际工况下的叶顶间隙流动雷诺数(特征长度取间隙高度，速度取间隙进口质量加权平均流速)确定了本文的计算工况。考虑到工况变化的影响，计算了4种雷诺数(Re=3 130、7 467、9 595和10 333)下的叶尖泄漏量，这些叶尖泄漏量随网格数的变化规律如图3(以Re=10 333为例)所示。由图3可知，网格数超过130万后，叶尖泄漏量变化不明显。因此，本文数值计算模型的网格都在130万左右，近壁面区无量纲壁面距离Y+小于40。

1.2 湍流模型、流体物性及边界条件

湍流模型选取Realizablek-ε模型，采用标准壁面函数、无滑移边界条件处理边界层与主流速度分布衔接。流体物性按理想气体处理，暂不考虑温度对流场的影响，进口温度取300 K。进口给定总压110 325 Pa，出口给定静压101 325 Pa，进出口压比约为1.09。进口湍流强度为0.5%，周向边界按周期性边界给定。

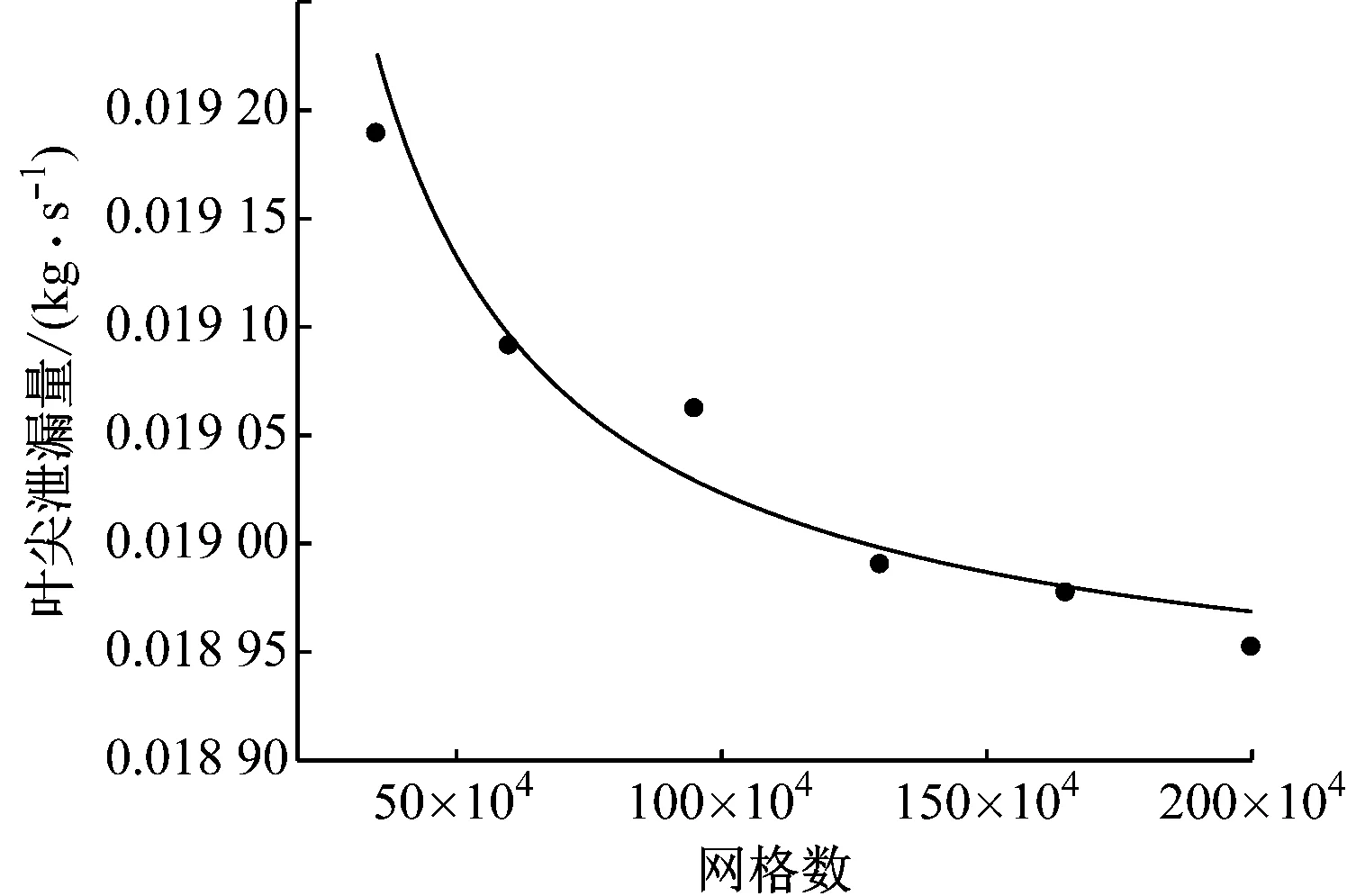
图3 叶尖泄漏量随网格数的变化曲线Fig.3 Tip leakage vs. grid number

1.3 数值方法及模型正确性验证

采用商业程序Ansys Fluent12.0求解控制方程，二阶迎风格式离散对流项，中心差分格式离散扩散项，采用基于Simple算法的数值求解方法和分离式求解器。在计算过程中，除能量方程残差下降6个数量级外，其他方程残差下降5个数量级视作收敛。

笔者曾利用文献[17]中的实验数据对带有叶尖自发射流的叶栅流动计算模型进行实验验证，计算结果与实验结果吻合较好，如图4所示[17]，其中C为轴向弦长，Cp为压力系数。在流动特征和几何尺度基本不变的前提下，认为针对原始模型的正确性验证仍然适用于本文的简化模型。

图4 本文计算结果与文献[17]实验结果的比较Fig.4 Comparison of calculation results by the method proposed and that in literature [17]

2 计算结果及分析

首先利用正交试验法优化自发射流参数，在此基础上，探讨了自发射流耦合叶顶凹槽对叶尖泄漏抑制效果的影响。

2.1 射流参数的正交数值优化

利用正交试验法，设计了3因素3水平正交表L9-3-4。待优化的三因素A、B、C分别对应间隙高度t、射流角和射流偏转角β(见图5)；因素A选取的3水平分别为0.5 mm、1 mm和2 mm(即t=0.25%h、0.5%h、1%h，其中h为叶高)；因素B选取的3水平分别为30°、50°和70°；因素C选取的3水平分别为0°、30°和60°。根据选定工况建立对应的数值计算模型，以叶尖泄漏量为衡量指标开展计算，试验方案及计算结果如表2所示。对该正交试验结果进行方差分析，结果见表3，其中显著水平的α值取0.05，以此来检验各因素对叶尖泄漏影响的显著性。

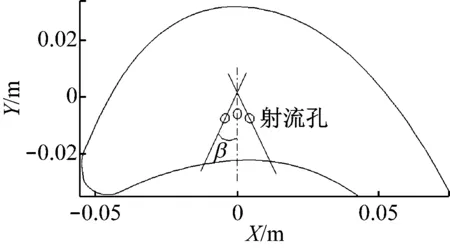
图5 射流偏转角β偏转方向示意图Fig.5 Schematic diagram of deviation angle β表2 正交试验方案及极差分析Tab.2 Orthogonal experiment scheme and the range analysis

名称A间隙高度/mmB射流角/(°)C射流偏转角/(°)误差D叶尖泄漏量/(kg·s-1)编号10.5300121.27×10-4编号20.55030221.45×10-4编号30.57060321.62×10-4编号413030374.22×10-4编号515060174.95×10-4编号61700274.80×10-4编号7230602179.22×10-4编号825003178.98×10-4编号9270301179.60×10-4均值121.4591.5791.6891.94均值274.6691.7991.7691.82均值3179.2792.0191.9391.61极差157.820.440.240.34

由表3可知，因素A的F比远远大于因素B和因素C，说明其对叶尖泄漏的影响十分显著，因素B和因素C对叶尖泄漏的影响则小得多。此外，表2中误差D的极差远远小于因素A的极差，且小于因素B的极差，因此可认为因素间的交互作用较小，可不考虑。

根据表2中的正交试验结果，结合均值和极差分析，确定最优的自发射流参数组合为A1B1C1，即间隙高度为0.5 mm(t=0.25%h)，射流角为30°，射流偏转角β为0°。

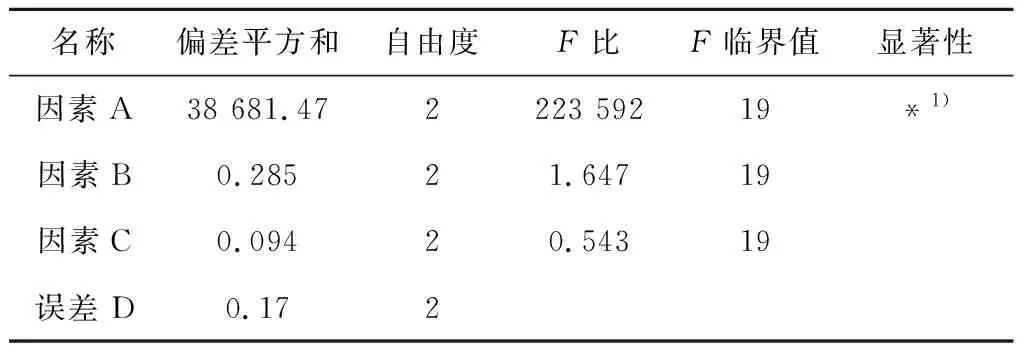
表3 叶尖泄漏方差分析表Tab.3 Variance analysis of tip leakage

注:1)代表该因素显著

2.2 自发射流耦合叶顶凹槽抑制叶尖泄漏研究

考虑到自发射流与叶尖开槽两者之间存在显著的气固耦合作用，将自发射流与凹槽耦合，探讨凹槽宽度和深度对耦合模型抑制叶尖泄漏效果的影响。

基础模型参数按第2.1节中优化后的结果选取，即t=0.25%h，射流角为30°，射流偏转角为0°。建模中固定凹槽前壁(靠近压力面)位置，改变凹槽宽度和深度。凹槽宽度分别取w=5%h、12.5%h和20%h，凹槽深度分别取d=0.5%h、1%h、2%h和4%h，部分耦合模型如图6所示。

d/h=0.5%d/h=1%d/h=2%

(a) w/h=5%

(b)d/h=4%

图6 部分自发射流与凹槽耦合模型

Fig.6 Partial model of spontaneous tip injection coupled with tip squealer

2.2.1 自发射流耦合叶顶凹槽对叶尖泄漏量的影响

通过计算得出各耦合模型的叶尖泄漏量，如图7所示。由图7可知，凹槽宽度对抑制泄漏有较大影响，图中直线为纯自发射流泄漏抑制水平参考线。在一定宽度范围内，凹槽宽度增加，叶尖泄漏量增大，甚至会大于纯自发射流的叶尖泄漏量，说明当凹槽过宽时，耦合模型的泄漏抑制效果会恶化，甚至不如单一方法的抑制效果好。而当凹槽宽度较小时，如w=5%h，自发射流与叶顶凹槽耦合能在纯自发射流基础上进一步提高叶尖泄漏抑制效果，这与文献[6]中的结论基本一致，即小凹槽宽度可提高涡轮效率。

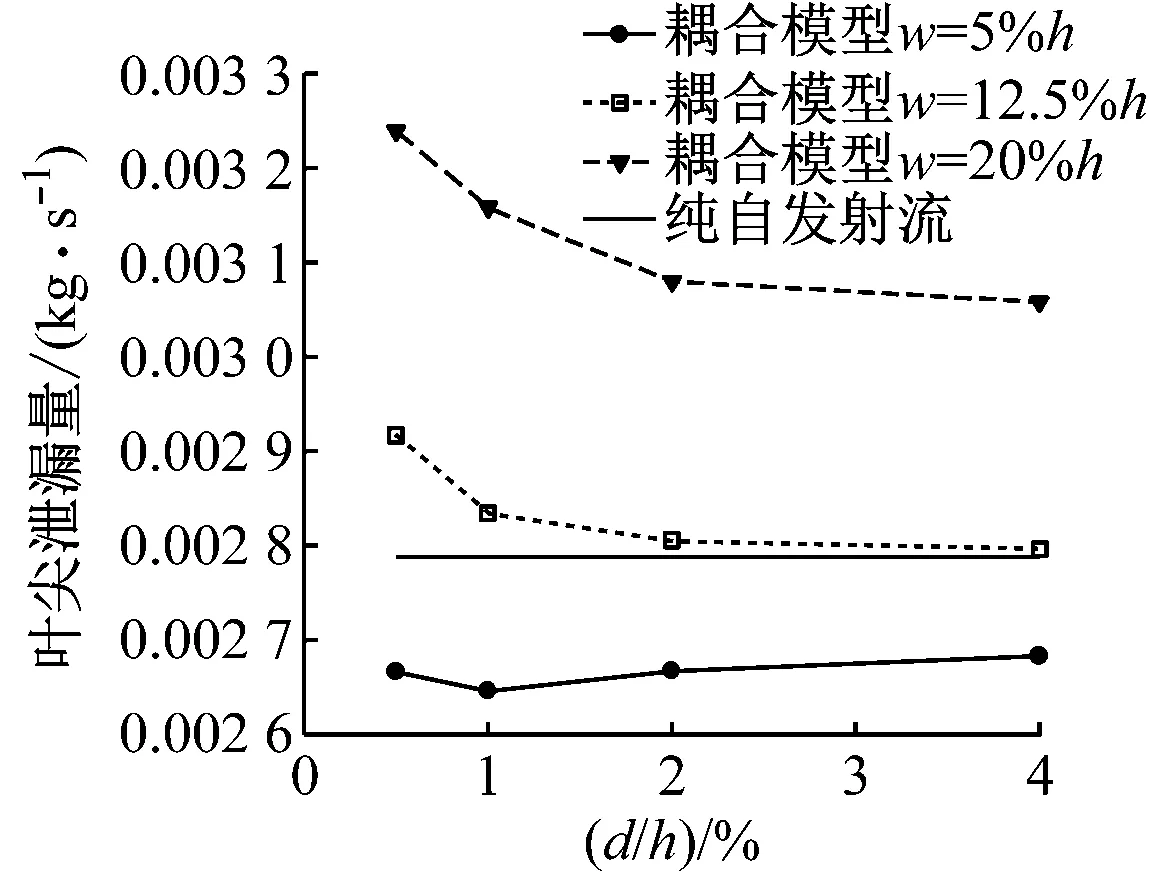
图7 不同w/h和d/h作用下的叶尖泄漏量Fig.7 Tip leakage loss at different ratios of w/h and d/h

由图7还可知，凹槽深度对叶尖泄漏抑制也有一定影响。当w=12.5%h、20%h时，随着凹槽深度增加，叶尖泄漏量减小，即耦合模型的泄漏抑制效果在增强，当凹槽深度增加到一定程度时，泄漏抑制效果增加趋缓。而在凹槽宽度w=5%h时，耦合模型的泄漏抑制效果随着凹槽深度增加出现先增强后减弱的规律，即凹槽深度存在最优值，而文献[3]中也存在最佳肋条高度。

2.2.2 自发射流耦合叶顶凹槽的流动特征及损失分布

选取2种凹槽宽度的耦合模型，对比其间隙内流线，如图8所示。由图8可知，自发射流在叶顶经射流孔喷射而出，形成相对于泄漏流的逆向气流，实现了对叶尖泄漏的第一次抑制。随后，泄漏流掠过叶尖凹槽上方，因黏性作用对凹槽腔内流体进行高速剪切，形成腔内漩涡，通过漩涡与内壁的摩擦作用，流体的能量不断耗散，之后又不断从泄漏流中吸收能量，其本质是消耗了泄漏流动能，实现了对叶尖泄漏的第二次抑制。

(a) w/h=5%，d/h=4%

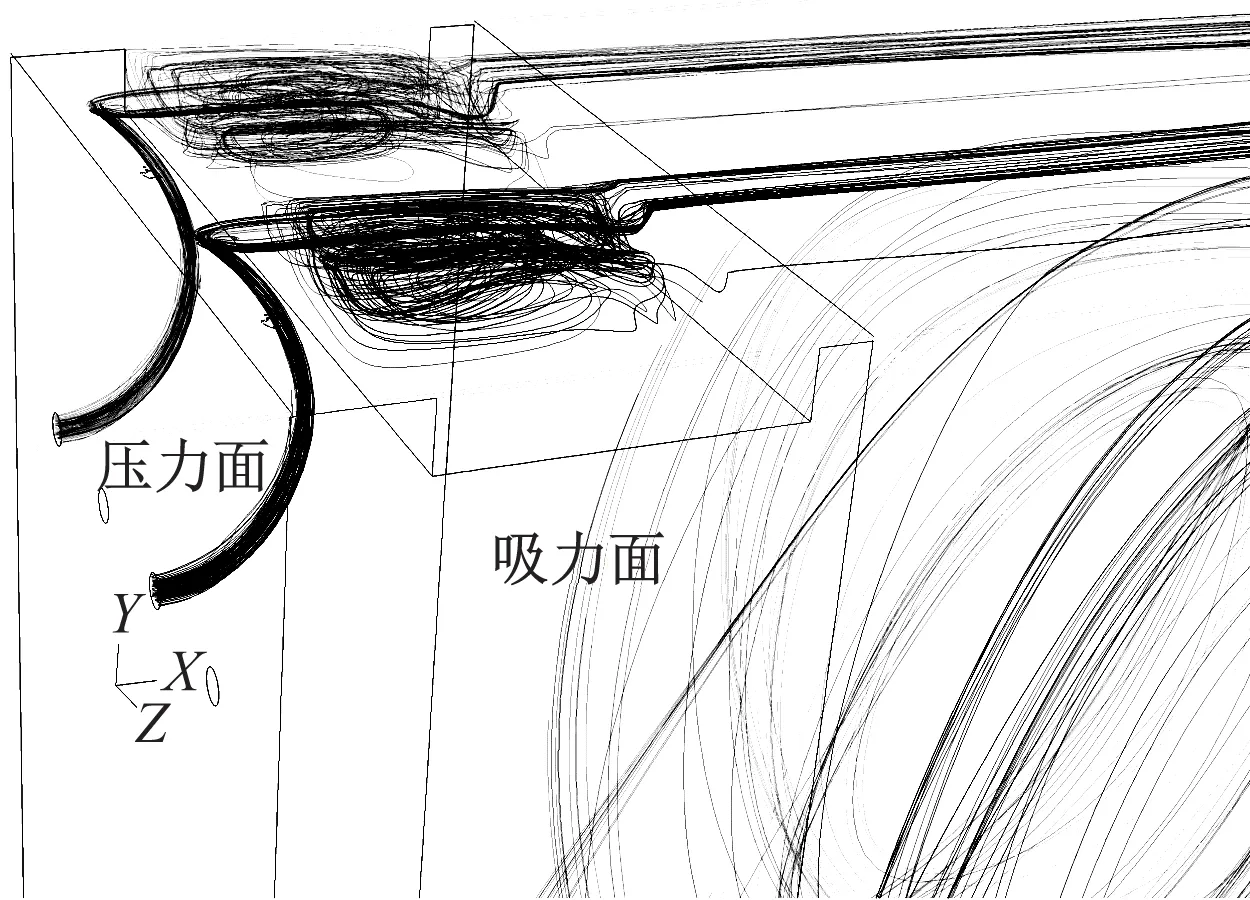
(b) w/h=20%，d/h=4%图8 典型耦合模型流线图Fig.8 Typical streamlines of spontaneous tip injection coupled with tip squealer

对比流线可知，当凹槽宽度较小时，凹槽内形成较规则的回流气流，贴壁效应较强，摩擦耗散也更为剧烈，因此泄漏抑制效果好。而当凹槽宽度较大时，凹槽内气流紊流度较大，做无规则混乱运动，流体动能耗散不佳，因此导致泄漏抑制效果变差。

图9和图10给出了不同凹槽宽度和深度下的速度流场。由图9可知，当凹槽宽度为w=5%h时，仅在靠近压力面凹槽的角隅处有泄漏涡。当d=1%h时，在凹槽内碰撞反射回流的流体速度方向角θ(θ为速度与X负半轴的夹角)较d=0.5%h时大，说明这股流动阻挡了间隙泄漏流动，起到了空气幕的作用，被阻挡后改变方向的流体撞向凹槽前壁，通过反复的碰撞、转向在靠近压力面凹槽底部形成逆时针泄漏涡，进一步阻挡了间隙流动。这说明随着凹槽深度的增加，泄漏抑制效果变好。

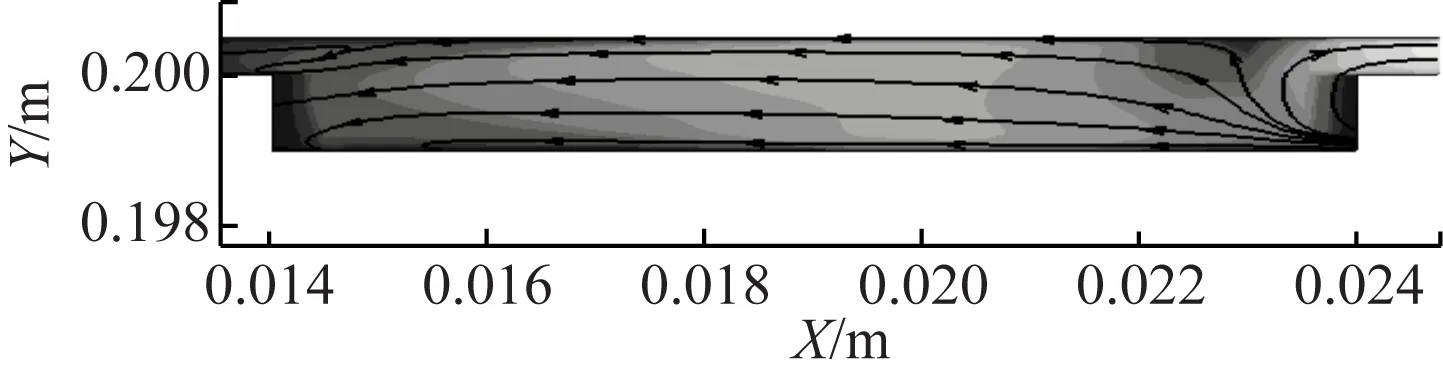
(a) w/h=5%，d/h=0.5%

(b) w/h=5%，d/h=1%

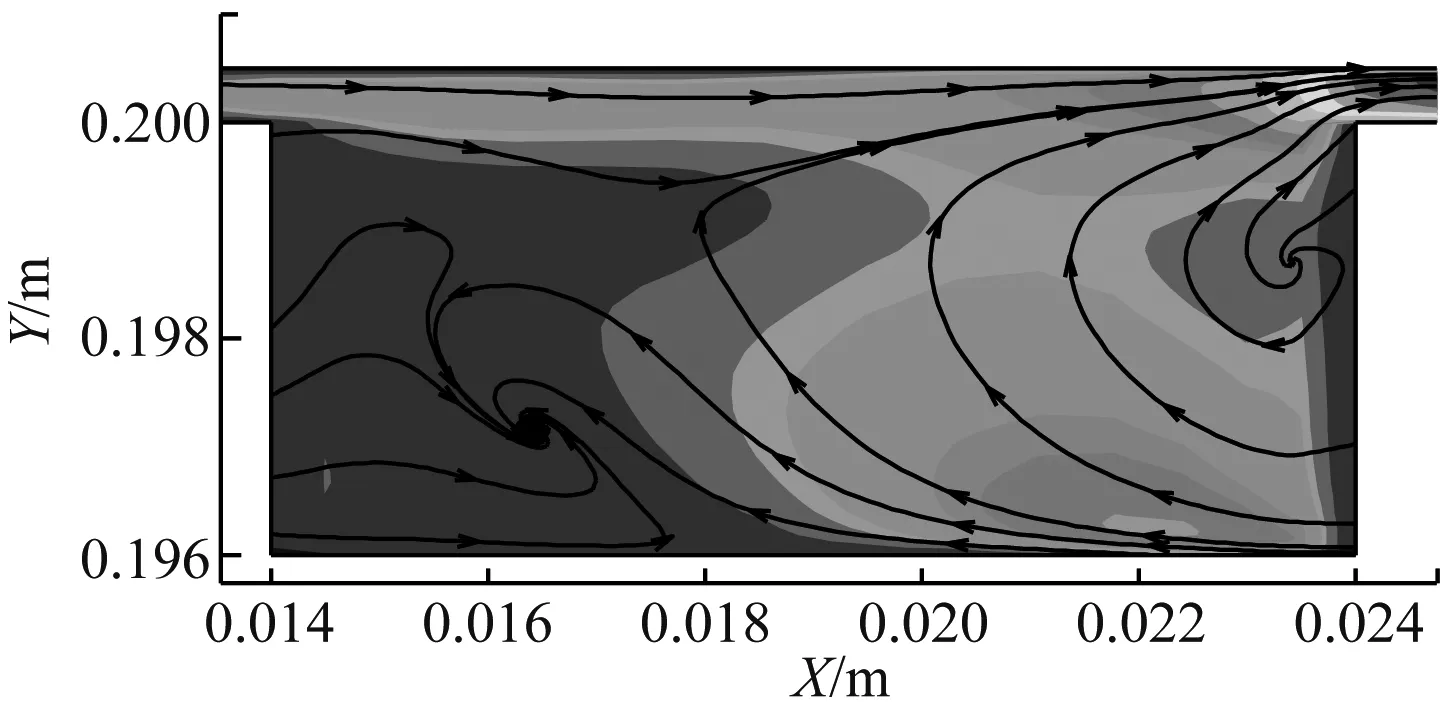
(c) w/h=5%，d/h=2%

图9 不同d/h下的速度流场

Fig.9 Velocity fields at different ratios ofd/h

随着凹槽深度继续增加，流体在凹槽内得到缓冲，反向回流速度降低，尤其是接近凹槽后壁处形成顺时针速度漩涡，此时对泄漏流动已无阻挡作用或阻挡作用甚微，因此泄漏抑制效果在凹槽深度增加到一定程度后恶化。

由图10可知，在凹槽深度不变的情况下(d=4%h)，随着凹槽宽度增加，间隙流体在凹槽内得到缓冲，流体间及流体与固壁的碰撞与摩擦所产生的损失减小，总压损失也减小。由图10还可知，随着凹槽宽度增加，泄漏涡尺度越来越小，最终导致泄漏抑制效果变差。

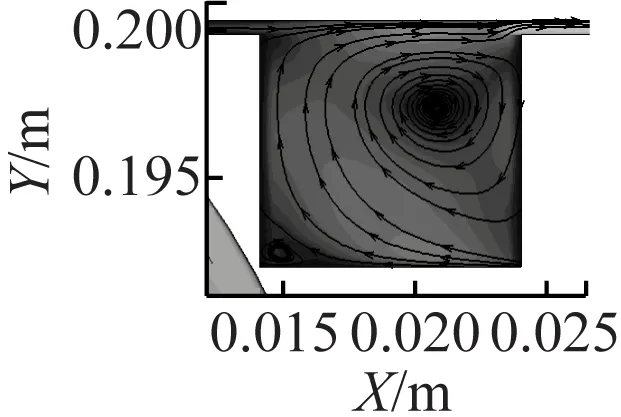
(a) w/h=5%，d/h=4%

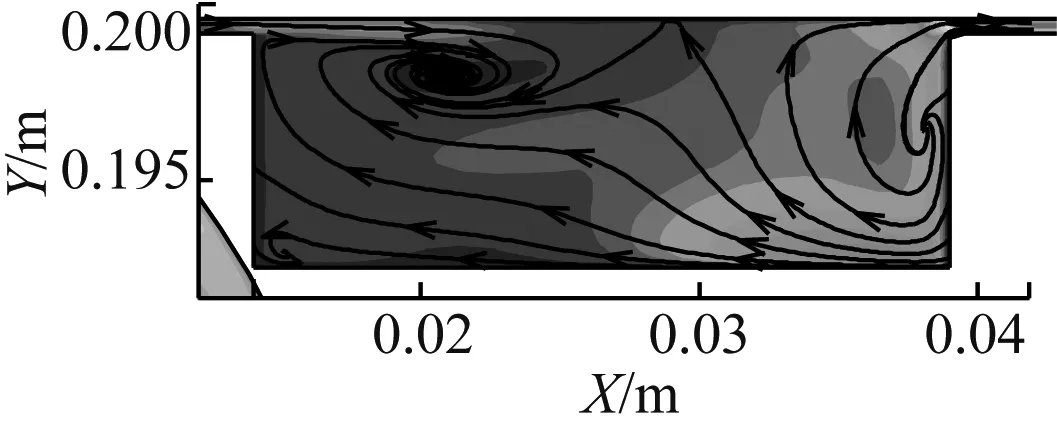
(b) w/h=12.5%，d/h=4%

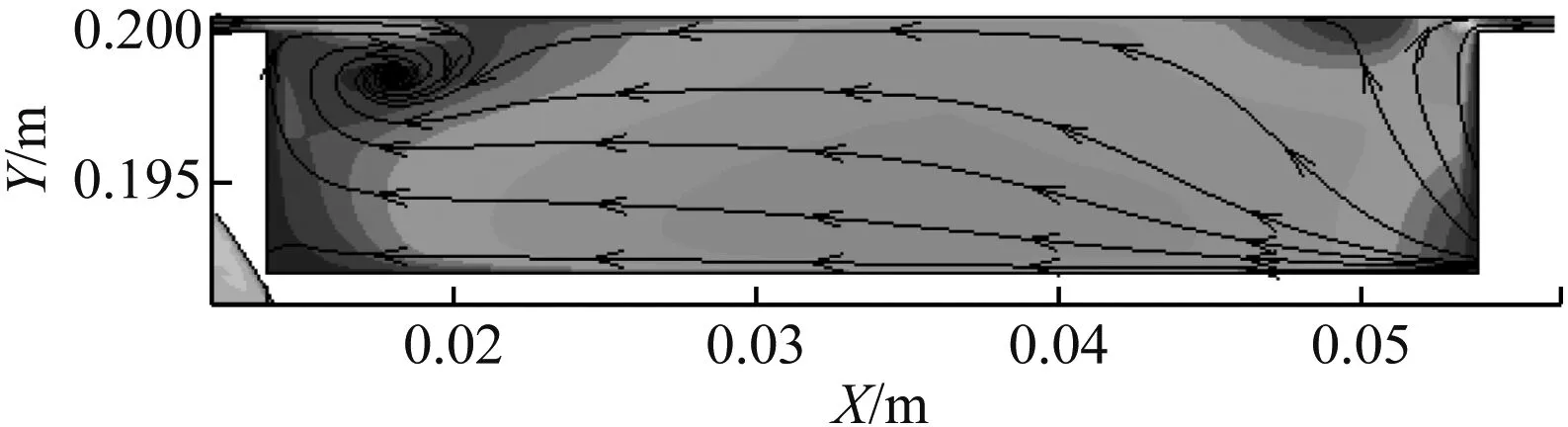
(c) w/h=20%，d/h=4%

图10 不同w/h下的速度流场

Fig.10 Velocity fields at different ratios ofw/h

为了揭示上述模型间隙内部流动损失的分布规律，沿着流体流动方向截取一系列截面，然后计算出截面的平均总压损失系数(见图11)。平均总压损失系数Cp,t定义为

(1)

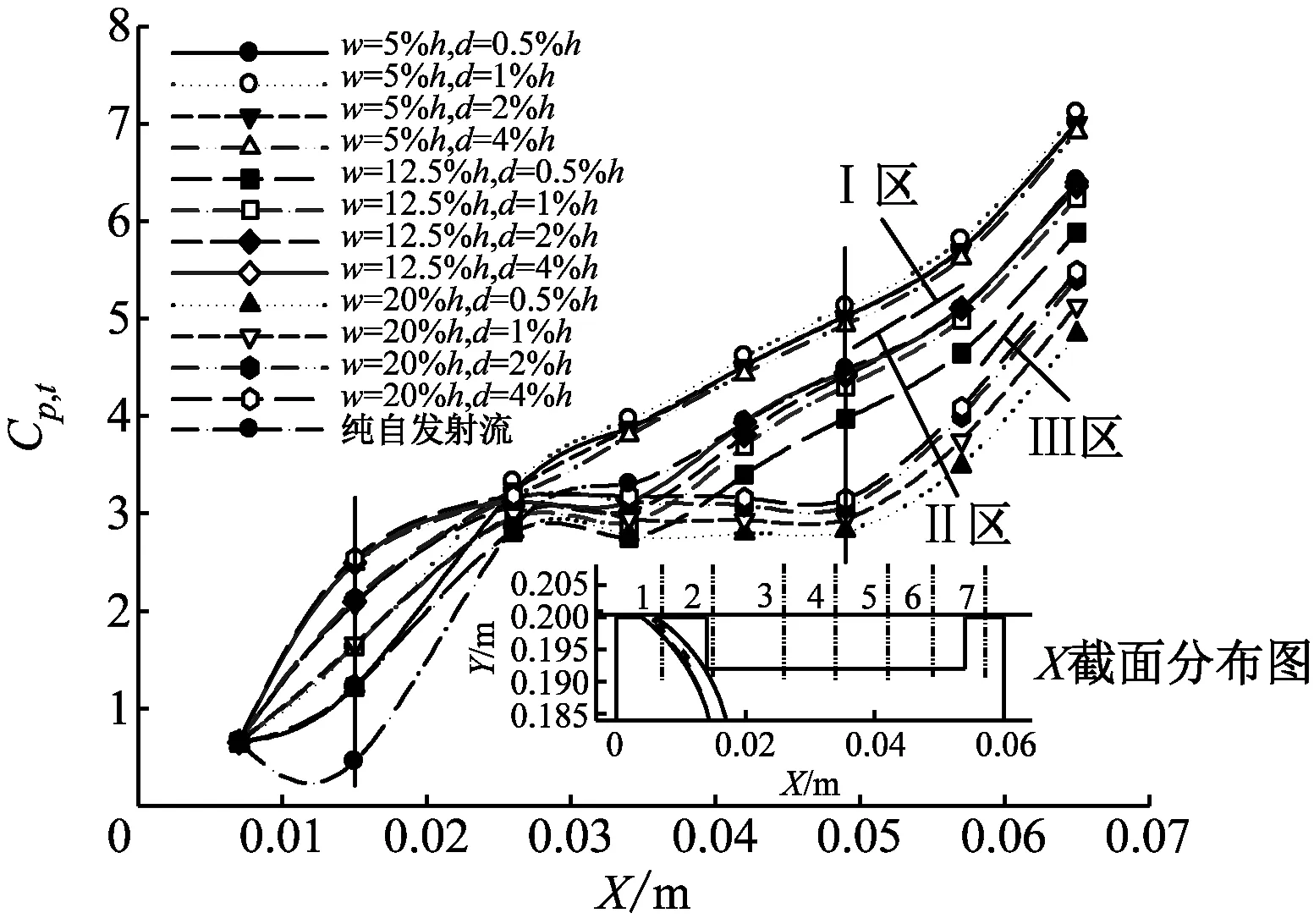
图11 典型截面的平均总压损失系数Fig.11 Cp,t of typical sections in all cases

由图11可知，截面2～截面6经过凹槽，根据凹槽内截面平均总压损失系数分布规律不同，可将12个工况划分为3个区域：Ⅰ、Ⅱ和Ⅲ，分别代表w=5%h、12.5%h和20%h，其中纯自发射流处在Ⅱ区。其中，Ⅰ区的特征为间隙内平均总压损失系数沿流向呈线性增大的趋势，Ⅲ区的特征为截面3之前间隙内平均总压损失系数基本呈线性增大，而截面3之后平均总压损失系数基本持平，Ⅱ区的特征介于两者之间。这与图9和图10中基于泄漏流场分析获得泄漏抑制效果优劣的结论基本一致，即平均总压损失越大，泄漏流动能耗散越大，叶尖泄漏量就越小，即泄漏抑制效果越好。

3 结 论

(1)采用正交试验法对射流参数进行优化，得到最优自发射流参数组合为A1B1C1，即间隙高度为0.5 mm(t=0.25%h)、射流角为30°、射流偏转角β为0°。

(2)叶顶凹槽宽度w/h对叶尖泄漏有较大影响。当w/h较小时，耦合结构较纯自发射流的间隙内部损失更大，叶尖泄漏量更小。而当w/h较大时，耦合结构的泄漏抑制效果恶化，甚至较纯自发射流差，应尽量避免这种组合方式。

(3)叶顶凹槽深度d/h对涡轮叶尖泄漏也有一定影响。当w/h较小，自发射流与叶顶凹槽耦合时存在最佳凹槽深度，即w=5%h，d=1%h；当w/h较大时，耦合结构的泄漏抑制效果随着d/h增加先急剧增强后趋于平缓。

(4)凹槽内漩涡尺度越大，涡系结构越清晰，平均总压损失系数越大，泄漏抑制效果越好。