电站锅炉再热蒸汽温度的燃烧器摆角和喷水减温协调预测控制
王东风, 李 玲, 王玉华
(华北电力大学 自动化系, 河北保定 071003)
火力发电生产过程中,蒸汽温度的控制比较困难。电网调度导致的扰动往往造成蒸汽温度波动较大[1-3]。对目前的大多数电站锅炉来说,蒸汽温度的控制主要有过热蒸汽温度和再热蒸汽温度的控制。对于过热蒸汽温度控制,这方面的研究相对较多,而对于再热蒸汽温度控制的研究相对较少。
再热蒸汽温度控制方法主要有常规串级比例积分微分(PID)控制、模糊控制和内模控制等策略。常规串级PID控制是目前火电厂再热蒸汽温度最常用的控制方法之一。但由于再热蒸汽温度对象存在惯性大、迟延大、参数受时间和机组负荷变化影响大等特点,当机组负荷出现较大变化时,串级PID方法经常出现超温现象[4],控制品质不理想。模糊控制常被应用到复杂被控系统,但该方法属于“事后控制型”,仅是根据被控对象目前的偏差来调整控制量大小,对于再热蒸汽温度对象来说,模糊控制对控制量的变化反应能力较差[5]。内模控制具有构架简单、调节性能优良等特点,对系统鲁棒性及抗干扰性具有良好的改善效果,能较好地控制大迟滞系统。将内模控制与PID控制结合的串级系统应用于再热蒸汽温度控制,内回路既可优化对象的动态特性,又能及时消除内扰[2],但内模控制对系统数学模型的精度要求相对较高。
再热蒸汽温度的控制手段主要有摆动燃烧器调节、烟气挡板调节、汽-汽换热器调节以及喷水减温调节等[6-7]。烟气挡板调节的优点有结构简单、方便操作,不会因煤种不同对炉膛燃烧造成影响,但是挡板易因受热变形而影响调温的精度,烟气挡板与再热蒸汽温度变化间的线性度差,调温延迟较大,容易使烟气挡板和减温水调节配合不当造成2个控制回路的震荡。燃烧器调节具有经济且控制范围大的特点,可调节的温度波动范围可达到±50 K。但由于燃烧器摆角过大时会加重燃料的不完全燃烧热损耗,摆角过小时又会出现冷灰斗结渣现象。因此,一般采用上述前3种调节方式中的一种作为主要调节方式u1,同时将喷水减温调节作为紧急使用的调节方式u2,前者是一种经济的调节方式,而后者只是作为紧急情况下的辅助手段,不宜长期使用,一般只在设备超温保护时才使用。
因此,控制量u1以摆动燃烧器调节为例进行讨论。在联合投入使用时可分为4种组合:(I)u1=u2=0;(II)u1≥0,u2=0;(III)u1=0,u2≥0;(IV)u1>0,u2>0。其中,u1>0表明需要燃烧器摆角控制维持正常的再热蒸汽温度(否则导致再热蒸汽温度偏低),u2>0表明需要喷水减温控制维持正常的再热蒸汽温度(否则导致超温)。情形(I)表明燃烧器摆角和喷水减温均不需要控制而再热蒸汽温度就能维持在期望值,这种情况极少出现;情形(II)表明需要燃烧器摆角而不需要喷水减温控制来维持再热蒸汽温度在期望值,这种情况是最经济的;情形(III)表明不需要燃烧器摆角控制而需要喷水减温控制来维持再热汽温在期望值,这种情况若发生了,是需要暂时使用的,但是不经济;情形(IV)表明燃烧器摆角和喷水减温需要同时参与控制来维持再热蒸汽温度在期望值,这种情形是需要极力避免的。
由此可见,燃烧器摆角和喷水减温共同维持再热蒸汽温度是必要的,但二者不能同时参与调节,任意时刻最多只能使用一种调节方式。目前,再热蒸汽温度控制主要存在2方面问题:(1)虽然设计有一定的燃烧器摆角和喷水减温配合控制逻辑,但二者经常是拉锯式的来回切换,造成不必要的能量消耗,或者是切换严重滞后而影响蒸汽调节效果;(2)常规控制方法对于具有很大惯性和迟延的再热蒸汽温度系统来说,很难获得满意的调节品质[7-8]。
综上所述,已有的锅炉再热蒸汽温度控制方法仍存在一定的局限性,鉴于预测控制的设计理念和方法[9-12],笔者从切换逻辑设计和控制方法选择2方面进行改进,提出了一种燃烧器摆角和喷水减温协调配合的电站锅炉再热蒸汽温度预测控制方法,大幅减少喷水的使用,提高机组热经济性。
1 再热蒸汽温度预测控制模型及方法
1.1 预测控制模型描述及其获取
所研究的再热蒸汽温度过程数学模型包括燃烧器摆角控制量u1-再热蒸汽温度y的模型G1以及喷水减温控制量u2-再热蒸汽温度y的模型G2,差分方程模型如下:
(1)
(2)
式中:t为当前采样控制时刻;y(t-i)为再热蒸汽温度在(t-i)时刻的值;u1(t-j)为u1在(t-j)时刻的值;u2(t-j)为u2在(t-j)时刻的值;na、nb、nc和nd分别为模型阶次,取值范围一般为na=nb=3~6、nc=nd=3~6,一般来说,取值越大模型越精确但计算量增加,本文均取为3;ai、bj、ci和dj均为模型系数,可以采用最小二乘[13]等方法辨识得到。
1.2 广义预测控制方法
广义预测控制方法(GPC)基于最小方差理论,将多步预测的思想引入到优化领域,从而明显增强系统的抗负载扰动、随机噪声和时延变化等能力,具有良好的鲁棒性,适用于纯迟延、开环不稳定的非最小相位系统[14]。另外,因其利用传统的参数模型,参数个数较少,对过程参数变化慢的系统易于实现参数在线估计,从而实现自适应控制。
在广义预测控制方法中,一般采用最小化参数模型[14],这类方法具有描述系统参数数目少,计算量相对小,适于在线实现等特点。
广义预测控制被控对象的数学模型采用如下离散差分方程[14]来描述:
A(z-1)y(t)=B(z-1)u(t-1)+C(z-1)ξ(t)/Δ
(3)
(4)
(5)
(6)
式中:y、u分别为系统输入输出;ξ为均值为零、方差为σ2的白噪声;Δ为差分算子。
假设系统时延d为离散时间控制系统的一步固有采样迟延1,若时延d>1,则只要令B(z-1)多项式内的前d-1项系数等于零。
针对被控对象式(1),j步最优预测输出为
(7)
式中:j为预测步数,j=1,2,…,N,N为最大预测时域长度。

gj-1z-(j-1)
(8)
多项式Ej(z-1)与Sj(z-1)可通过求解Diophantine方程得到:
1=Ej(z-1)A(z-1)Δ+z-1Sj(z-1)
(9)
(10)
(11)
式中:ei、si均为多项式系数。
广义预测控制采用对输出误差和控制增量加权的二次型性能指标:

(12)
式中:E(·)为期望;N1为最小预测长度,一般选N1=1,若已知系统时延,则取N1=d;M为控制时域长度,一般取M 基于最小方差理论可得广义预测最优控制律为 ΔU(t)=(GTQG+λ)-1GTQ[Yr(t+1)- F0ΔU(t-1)-S(z-1)y(t)] (13) 式中:λ为控制增量加权系数矩阵,λ=diag(λ1,λ2,…,λm),通常取常数;Q=diag(qN1,qN1+1,…,qN)。其他变量定义[14]如下: F0=[f0(t+1),f0(t+2),…,f0(t+N)]T (14) Yr(t+1)=[yr(t+1),yr(t+2),…,yr(t+N)]T (15) ΔU(t)=[Δu(t),Δu(t+1),…,Δu(t+M-1)]T (16) ΔU(t-1)=[Δu(t-nb),…,Δu(t-1)]T (17) G为N×M维矩阵: (18) 锅炉再热蒸汽温度的燃烧器摆角和喷水减温协调预测控制基于式(19)和式(20)所示的目标函数,采用广义预测控制方法进行求解,其中燃烧器摆角控制增量ΔU1(t)的目标函数J1(t)为 (19) s.t.u1,min≤u1(t)≤u1,max |Δu1(t)|≤Δu1,max 喷水减温控制增量ΔU2(t)的目标函数J2(t)为 (20) s.t.u2,min≤u2(t)≤u2,max |Δu2(t)|≤Δu2,max 式中:u1,max、u1,min分别为燃烧器摆角控制量的上、下限约束;Δu1,max为燃烧器摆角控制量的速率约束;u2,max、u2,min分别为喷水减温控制量的上、下限约束;Δu2,max为喷水减温控制量的速率约束;ΔU1(t)=[Δu1(t),Δu1(t+1),…,Δu1(t+M1-1)],表示t时刻求解的从现在时刻起到未来(t+M1-1)时刻止的M1个时刻燃烧器摆角控制增量;ΔU2(t)=[Δu2(t),Δu2(t+1),…,Δu2(t+M2-1)],表示t时刻求解的从现在时刻起到未来(t+M2-1)时刻止的M2个时刻的喷水减温控制增量。 燃烧器摆角控制向量U1(t)=[u1(t),u1(t+1),…,u1(t+M1-1)]和喷水减温控制向量U2(t)=[u2(t),u2(t+1),…,u2(t+M2-1)]计算式如下: U1(t)=U1(t-1)+ΔU1(t) (21) U2(t)=U2(t-1)+ΔU2(t) (22) 2.2.1 控制系统执行步骤 控制系统的执行步骤如下: (1) 确定协调预测控制的采样时间间隔Ts、蒸汽温度预测时域P、燃烧器摆角控制时域M1和喷水减温控制时域M2。 (2) 通过再热蒸汽温度控制系统特性试验,分别得到燃烧器摆角控制量u1和喷水减温控制量u2作用下的锅炉再热蒸汽温度y的数学模型。 (3) 将燃烧器摆角控制和喷水减温控制作为调节手段,采用模型预测控制分别求解ΔU1(t)和ΔU2(t)。 (4) 计算燃烧器摆角控制向量U1(t)和喷水减温控制向量U2(t)。 (5) 分别计算U1(t)和U2(t)与其下限约束之差D1(t)和D2(t)的斐波那契范数‖D1(t)‖、‖D2(t)‖。 (6) 根据范数‖D1(t)‖和‖D2(t)‖确定当前时刻t是采用燃烧器摆角控制还是采用喷水减温控制,并施加相应的控制作用对再热蒸汽温度进行调节。 ‖D1(t)‖和‖D2(t)‖的表达式如下: (23) (24) 其中,D1(t)=U1(t)-u1,min=[u1(t)-u1,min,u1(t+1)-u1,min,…,u1(t+M1-1)-u1,min],D2(t)=U2(t)-u2,min=[u2(t)-u2,min,u2(t+1)-u2,min,…,u2(t+M2-1)-u2,min]。 此外,步骤(6)中根据范数‖D1(t)‖和‖D2(t)‖确定t时刻的调节手段,是通过图1所示的运算流程实现的,具体流程见第2.2.2节。 2.2.2 预测控制方法运算流程 当本文预测控制方法获得接管再热蒸汽温度的控制权时,其方法流程为 s00.计算U2(t)与‖D2(t)‖,判断‖D2(t)‖是否几乎为零。若‖D2(t)‖≥δ1|,表明喷水减温控制正在进行调节,进入步骤s21;若‖D2(t)‖<δ1,表明喷水减温控制量几乎为零,因而进行燃烧器摆角控制计算,进入步骤s11(其中δ1是用来判断‖D2(t)‖是否几乎为零的阈值)。 图1 再热蒸汽温度的燃烧器摆角和喷水减温协调预测控制方法的运算流程图Fig.1 Flow chart of tilter and attemperator coordinated predictive control for reheated steam temperature s10.判断再热蒸汽温度测量值与设定值之间误差E是否几乎为零。若误差的绝对值|E|<δe,表明燃烧器摆角和喷水减温均几乎为零,无需调节,再热蒸汽温度即可良好地维持在设定值,回到步骤s25;若|E|≥δe,表明在喷水减温控制过程中,由于系统运行情况发生变化,需要关闭喷水减温控制作用,进行燃烧器摆角控制,进入步骤s11(其中δe是用来判断误差的绝对值|E|是否几乎为零的阈值)。 s11.基于J1(ΔU1(t)),根据式(13)和式(19)求解ΔU1(t)。 s12.根据式(21)计算U1(t)。 s13.根据式(23)计算D1(t)及‖D1(t)‖。 s14.判断‖D1(t)‖是否几乎为零。若‖D1(t)‖<δ1,进入步骤s20;若不是,即‖D1(t)‖≥δ1,则表明燃烧器摆角控制正在作用,进入步骤s15。 s15.设置u2(t)=u2,min,确保喷水减温不参与控制,进入步骤s30。 s20.判断再热蒸汽温度测量值与设定值之间误差E是否几乎为零。若|E|<δe,则表明燃烧器摆角和喷水减温均几乎为零,无需调节,再热蒸汽温度即可良好地维持在设定值,进入步骤s15;若|E|≥δe,则表明在燃烧器摆角控制过程中,由于系统运行情况发生变化,需要关闭燃烧器摆角控制,进行喷水减温控制,进入步骤s21。 s21.基于J2(ΔU2(t)),根据式(13)和式(20)求解ΔU2(t)。 s22.根据式(22)计算U2(t)。 s23.根据式(24)计算D2(t)及‖D2(t)‖。 s24.判断‖D2(t)‖是否几乎为零。若‖D2(t)‖<δ2,表明喷水减温控制量几乎为零,进入步骤s10;若‖D2(t)‖≥δ2,则表明喷水减温控制正在作用,进入步骤s25(其中δ2是用来判断‖D2(t)‖是否几乎为零的阈值)。 s25.设置u1(t)=u1,min,确保燃烧器摆角不参与控制,进入步骤s30。 s30.输出u1(t)、u2(t)到现场执行机构。 值得说明的是,由于常规控制的不合理可能存在‖D1(t)‖和‖D2(t)‖同时不为零,而此处总是保证二者至少有一个为零。步骤s00是指从常规控制或从运行人员手动操作切换到本文预测控制方法,具体是通过计算‖D2(t)‖,判断其是否几乎为零,然后根据结果选择进入燃烧器摆角调节或者喷水减温调节的预测控制量计算。这里不能通过判断‖D1(t)‖是否几乎为零来进行分支选择。因为使用‖D2(t)‖可能导致暂时性温度偏低,但很快会通过预测控制将温度调节到正常值,仅仅是暂时性导致机组效率偏低;而使用‖D1(t)‖可能导致暂时性温度偏高,虽然也会通过预测控制将温度调节到正常值,但是超温会影响设备寿命甚至机组安全,相对于前者来说其后果更严重。 为了测试锅炉再热蒸汽温度的燃烧器摆角与喷水减温协调预测控制方案,以某一负荷下的燃烧器摆角回路和减温喷水回路的被控对象模型为例进行仿真研究。 对某300 MW机组进行现场测试(采样周期Ts=5 s),获得u1-y和u2-y的数学模型分别如下: y(k)=2.661y(k-1)-2.36y(k-2) + 0.697 7y(k-3)+3.949×10-4u1(k-1) + 1.444×10-3u1(k-2)+3.299×10-4u1(k-3) (25) y(k)=2.715y(k-1)-2.456y(k-2) + 0.740 8× y(k-3)-1.083×10-4u2(k-1)-4.018×10-4u2(k-2)-9.318×10-5u2(k-3) (26) 为说明问题,假定u1调节范围为±10%,u2调节范围正常开度为0~100%。 再热蒸汽温度控制器采用GPC时,预测时域N=50,燃烧器摆角控制时域M1=5,喷水减温控制时域M2=5,柔化因子α=0.5,控制量加权系数λ=0.1。图2~图4分别给出了本文预测控制方法、一般预测控制和PID控制的对比仿真结果。在仿真实验过程中始终加入了噪声干扰,且在图中500~2 000 s以及2 500~3 500 s,再热蒸汽温度均受到燃烧扰动。由图2~图4可知,3种控制方案都能通过调整燃烧器摆角和喷水减温来抑制蒸汽温度波动,但是只有本文预测控制方法可以保证在任意时刻只有1种控制方案起作用:图2中,协调预测控制只有在1 500~3 000 s采用喷水减温调节,其余时段切换到燃烧器摆角调节;图4中,整个过程中PID控制都是在2种调节方案之间频繁切换。 (a) 再热蒸汽温度作10 K阶跃扰动后的调节曲线 (b) 控制增量Δu1和Δu2曲线 (c) u1和u2的控制切换情况图2 燃烧率扰动下的燃烧器摆角和喷水减温的 协调预测控制效果图 Fig.2 Effectiveness of tilter and attemperator coordinated predictive control with disturbance of combustion rate (a) 再热蒸汽温度作10 K阶跃扰动后的调节曲线 (b) 控制增量Δu1和Δu2曲线 (c) u1和u2的控制切换情况图3 燃烧率扰动下的燃烧器摆角和喷水减温的 一般预测控制效果图 Fig.3 Effectiveness of tilter and attemperator conventional predictive control with disturbance of combustion rate (a) 再热蒸汽温度作10 K阶跃扰动后的调节曲线 (b) 控制增量Δu1和Δu2曲线 (c) u1和u2的控制切换情况图4 燃烧率扰动下的燃烧器摆角和喷水减温的PID控制效果图Fig.4 Effectiveness of tilter and attemperator PID control with disturbance of combustion rate 通过对比可以看出,本文预测控制方法在燃烧器摆角与喷水减温的控制间切换是平稳而非频繁的,而常规调节方案在燃烧器摆角与喷水减温的控制间切换较频繁,本文预测控制方法的控制效果更好。 对于使用燃烧器摆角和喷水减温调节再热蒸汽温度的电站锅炉,在任意时刻只需要一种调节方式,即正常情况下只使用燃烧器摆角调节,在燃烧器摆角无调节能力时才使用喷水减温辅助调节。所设计的协调预测控制能够最大限度地达到这一目标,实现燃烧器摆角调节和喷水减温调节二者之间的平滑、无扰切换,因而能够大幅减少喷水的使用,提高再热蒸汽温度控制系统设备的使用寿命以及机组的热经济性,而常规调节方案在燃烧器摆角与喷水减温的控制间切换较频繁。所提出的预测控制方法具有更好的调节性能和稳定性,克服了常规设计控制方法的一些不良问题。2 再热蒸汽温度的燃烧器摆角和喷水减温协调预测控制
2.1 协调预测控制方法


2.2 协调预测控制步骤和流程

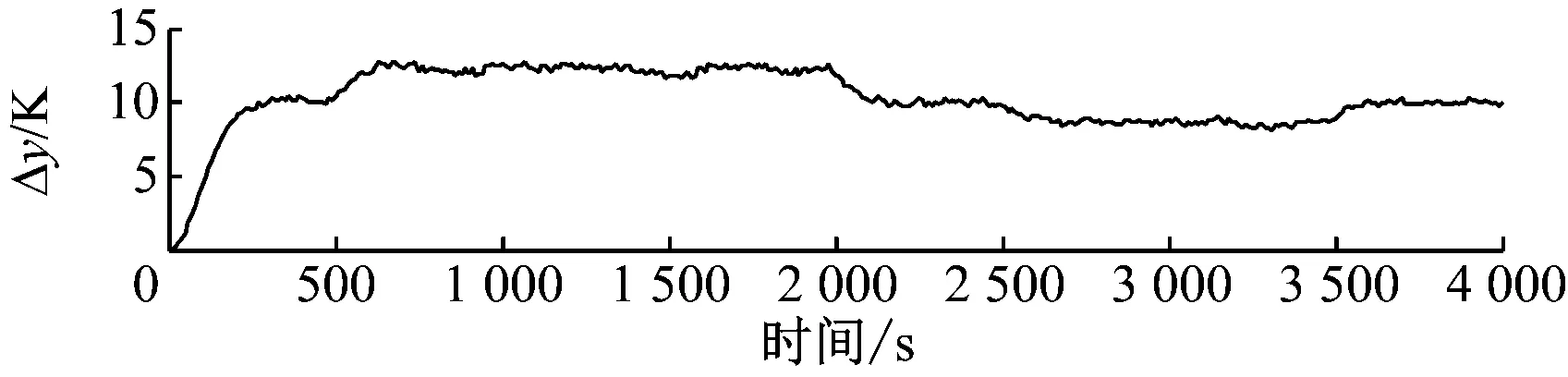
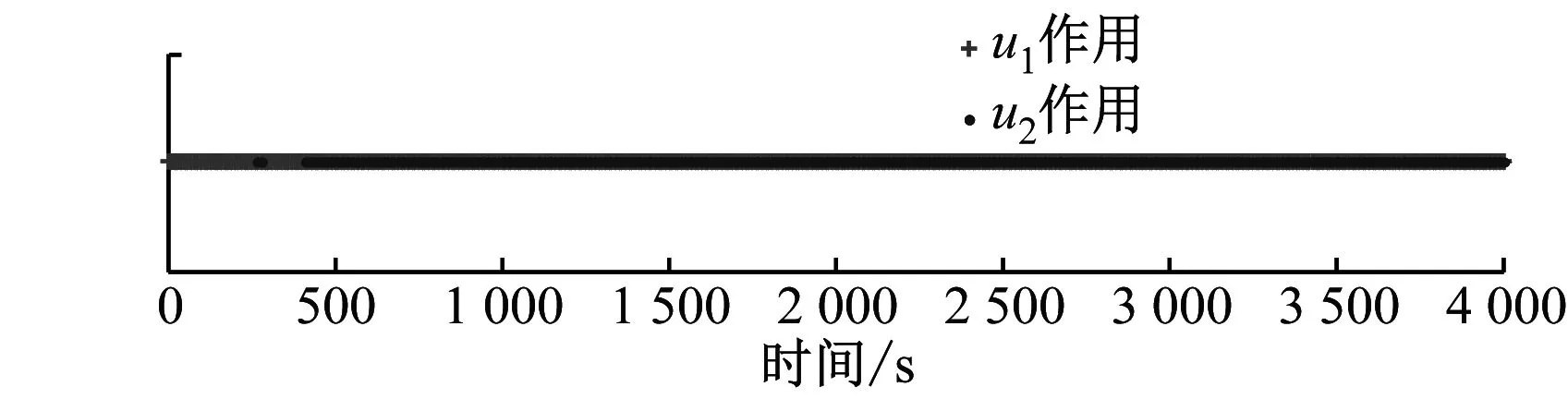
3 仿真实验结果及分析

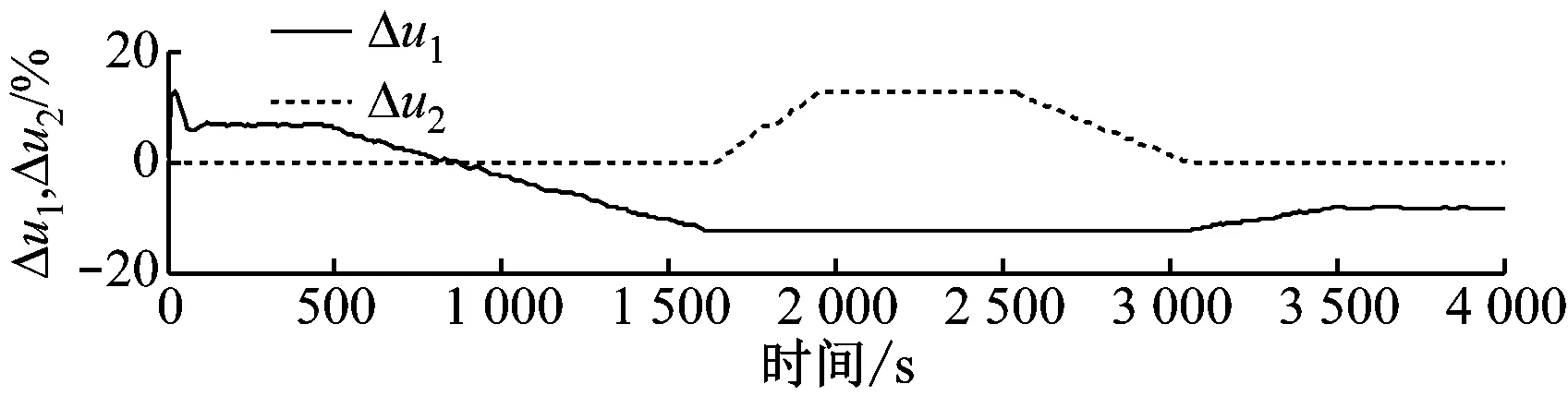

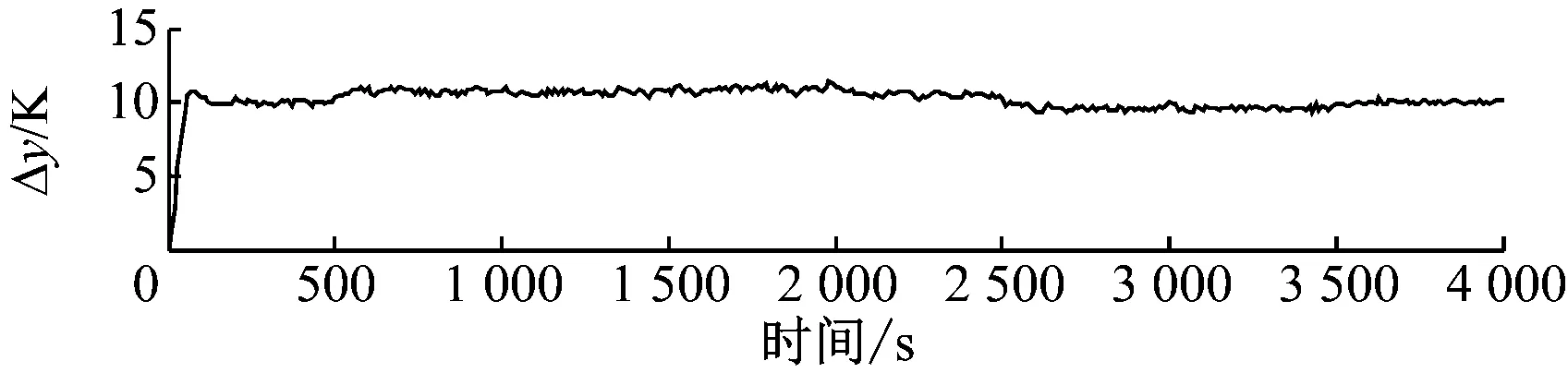
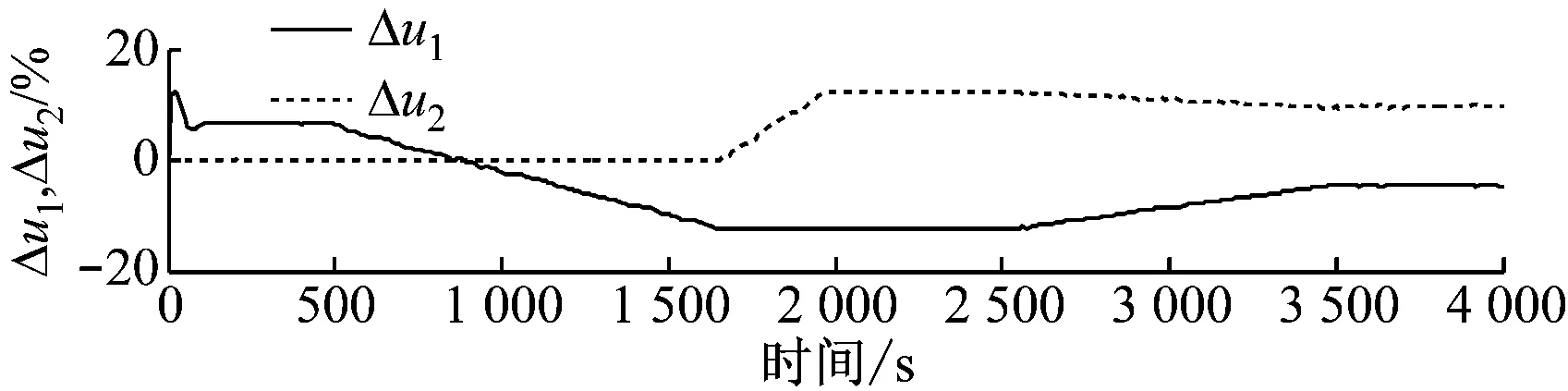
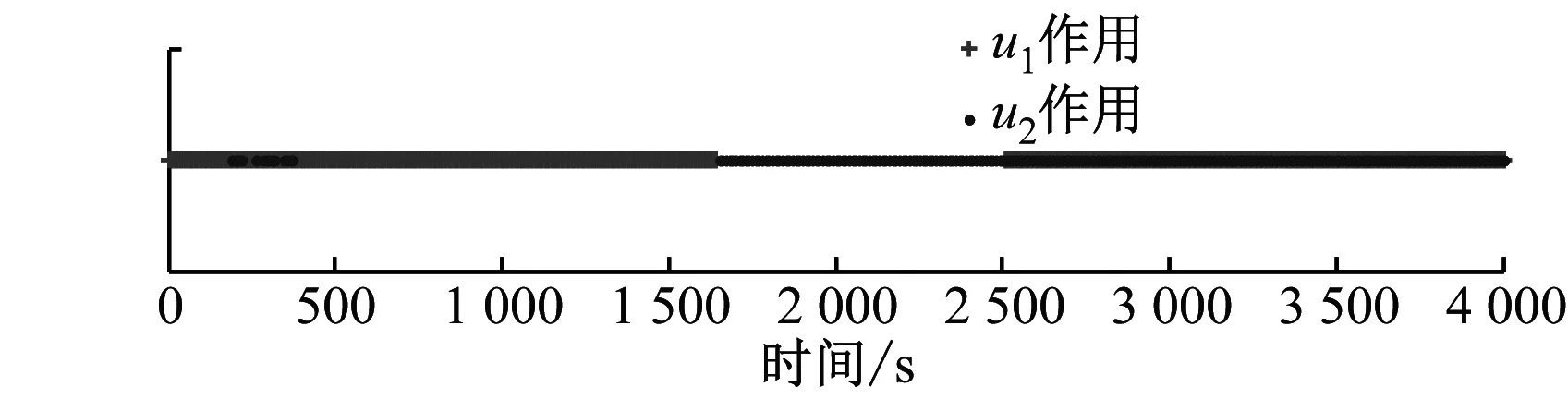

4 结 论

